- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Применение признаков равенства треугольников в задачах ГИА. Модуль Геометрия.
Содержание
- 1. Применение признаков равенства треугольников в задачах ГИА. Модуль Геометрия.
- 2. Высота, медиана, биссектриса треугольникаОтрезок, соединяющий вершину треугольника
- 3. Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним
- 4. Свойства равнобедренного треугольникаАСВВ равнобедренном треугольнике углы при основании равны
- 5. Свойства прямоугольного треугольникаСумма двух острых углов прямоугольного
- 6. Признаки равенства треугольниковI признакПо двум сторонам и
- 7. Признаки равенства прямоугольных треугольниковПо двум катетамЕсли АВ
- 8. Подобие треугольниковДва треугольника называются подобными, если их
- 9. Признаки подобия треугольников1. Если два угла одного
- 10. Слайд 10
- 11. Слайд 11
- 12. Слайд 12
- 13. Слайд 13
- 14. Слайд 14
- 15. Слайд 15
- 16. Слайд 16
- 17. Слайд 17
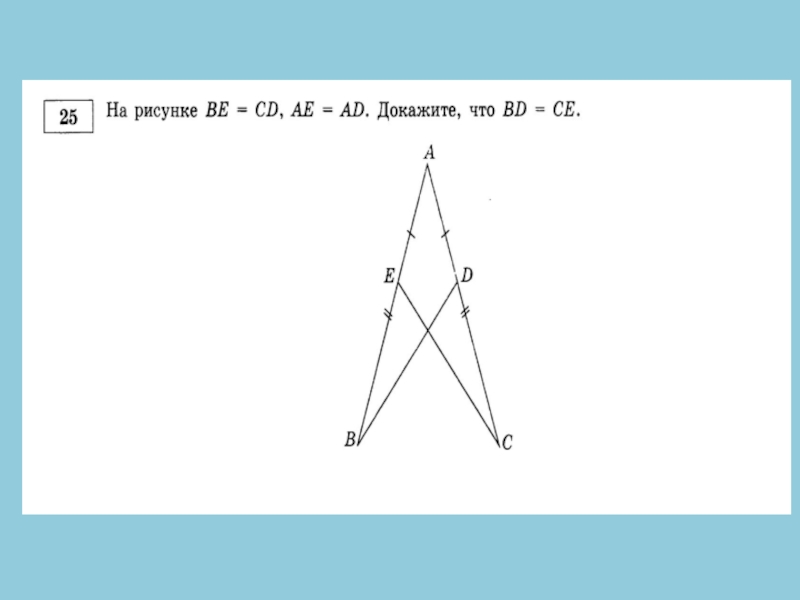
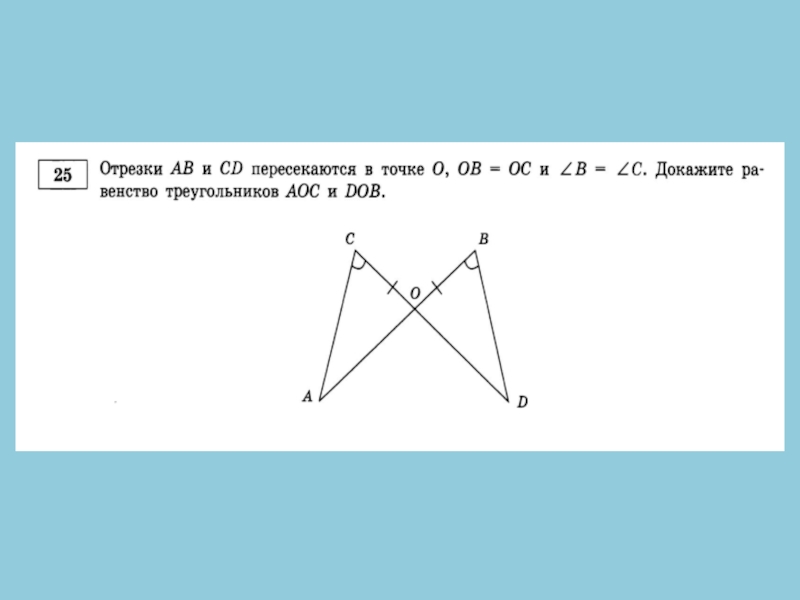
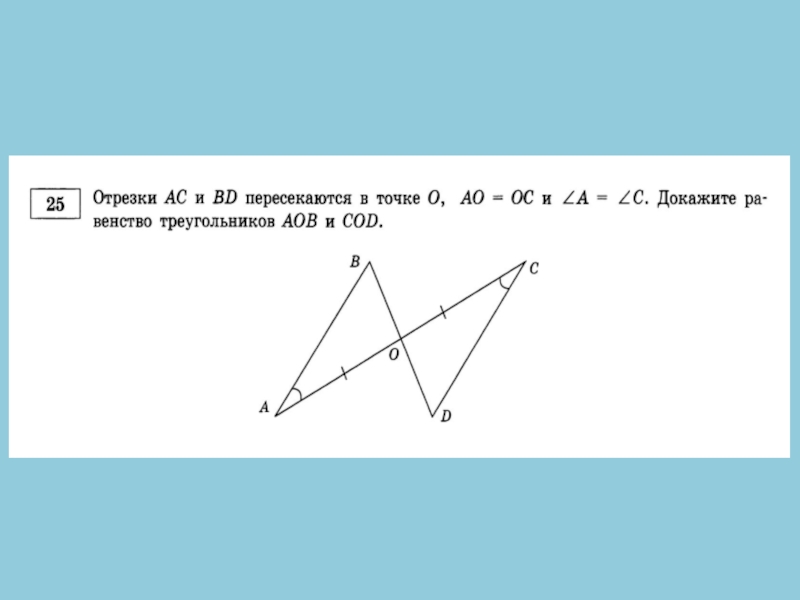
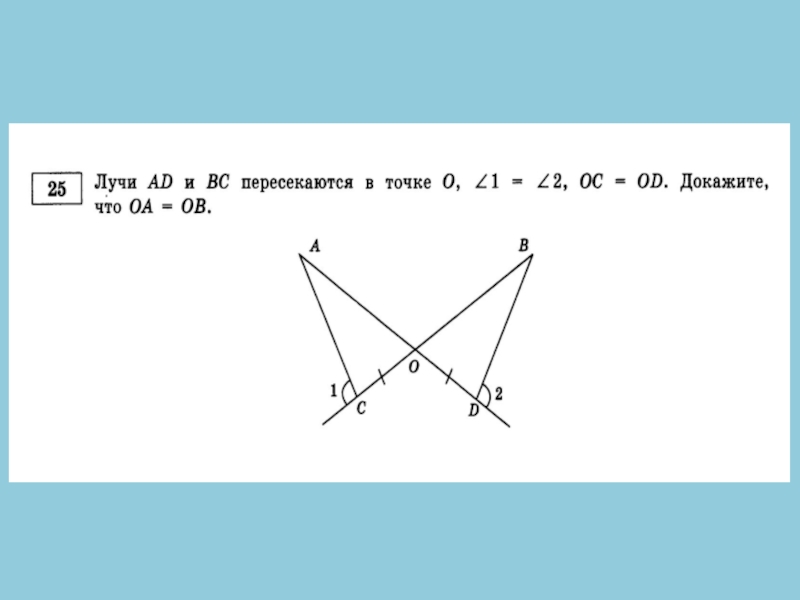
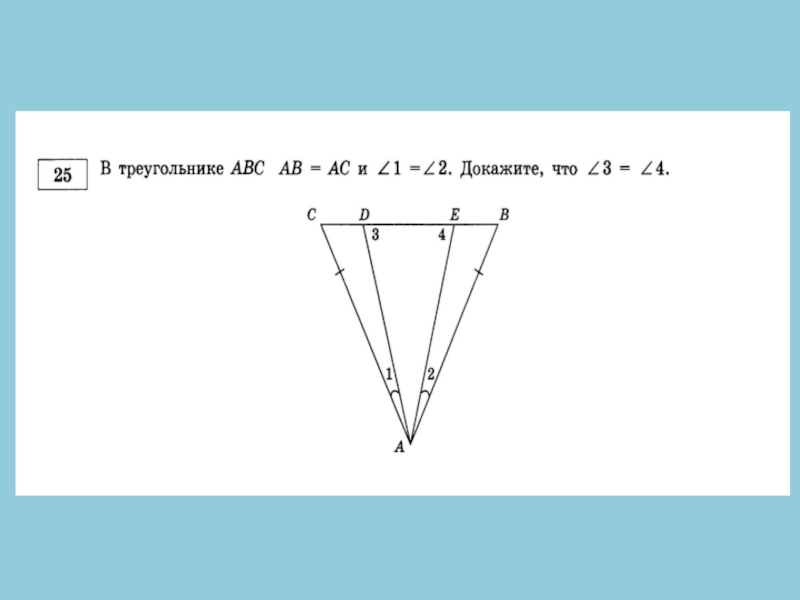
- 18. № 25. Отрезки АВ и CD пересекаются
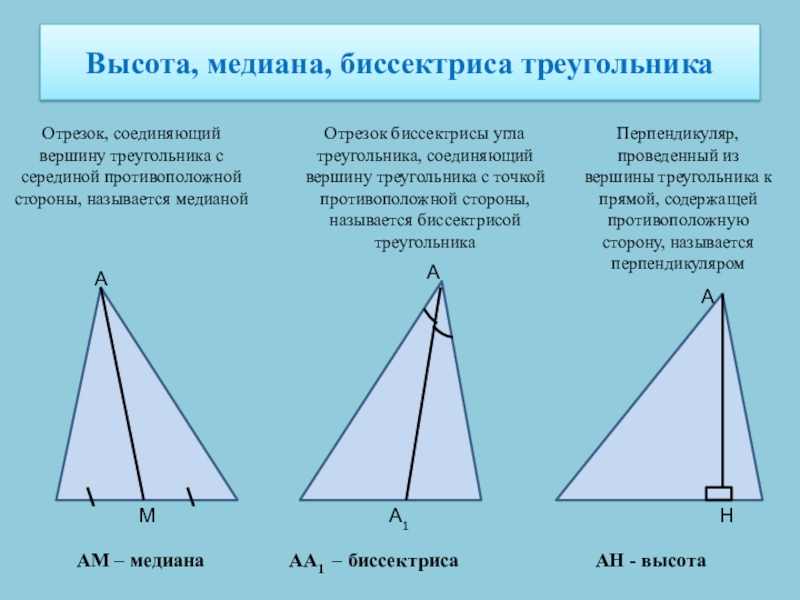
Слайд 2Высота, медиана, биссектриса треугольника
Отрезок, соединяющий вершину треугольника с серединой противоположной стороны,
А
М
АМ – медиана
Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны, называется биссектрисой треугольника
А
А1
АА1 – биссектриса
Перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону, называется перпендикуляром
Н
А
АН - высота
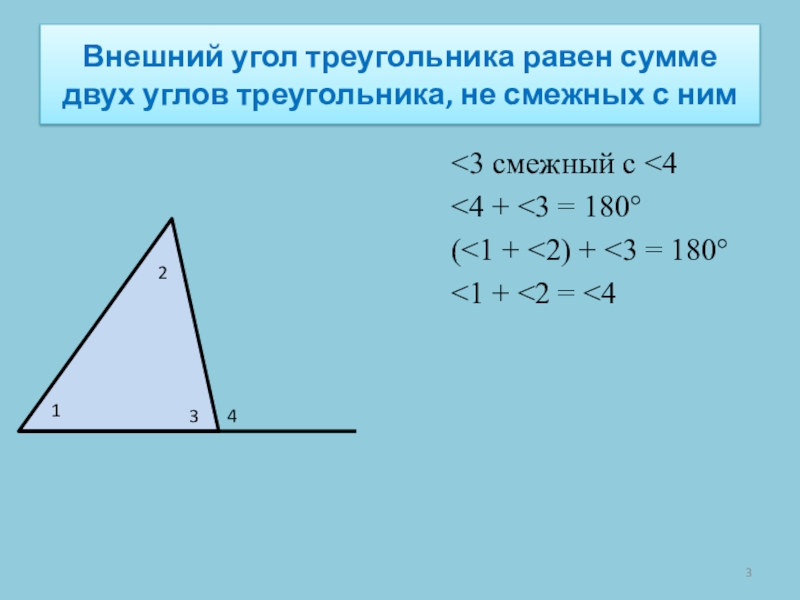
Слайд 3Внешний угол треугольника равен сумме двух углов треугольника, не смежных с
<3 смежный с <4
<4 + <3 = 180°
(<1 + <2) + <3 = 180°
<1 + <2 = <4
1
2
3
4
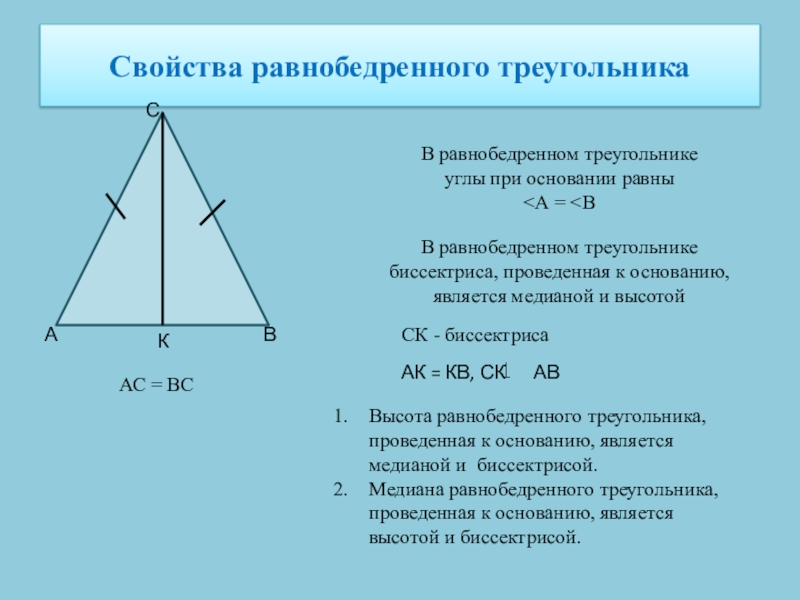
Слайд 4Свойства равнобедренного треугольника
А
С
В
В равнобедренном треугольнике углы при основании равны
АС = ВС
СК - биссектриса
К
АК = КВ, СК АВ
Высота равнобедренного треугольника, проведенная к основанию, является медианой и биссектрисой.
Медиана равнобедренного треугольника, проведенная к основанию, является высотой и биссектрисой.
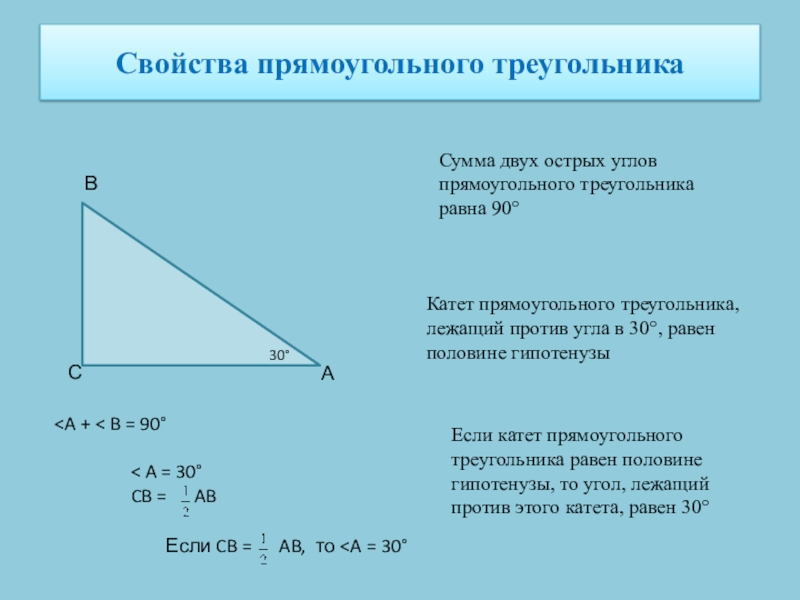
Слайд 5Свойства прямоугольного треугольника
Сумма двух острых углов прямоугольного треугольника равна 90°
Катет прямоугольного
Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против этого катета, равен 30°
С
А
В
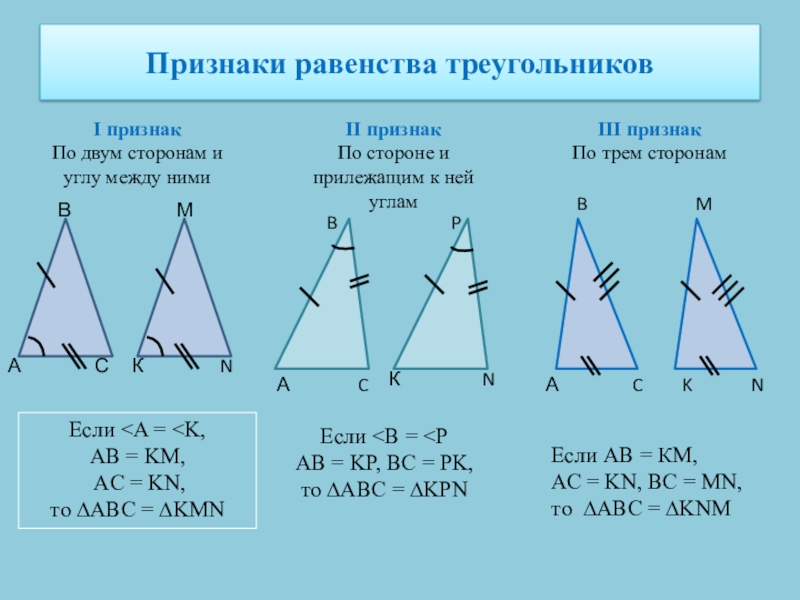
Слайд 6Признаки равенства треугольников
I признак
По двум сторонам и углу между ними
II признак
По
III признак
По трем сторонам
А
N
М
К
С
В
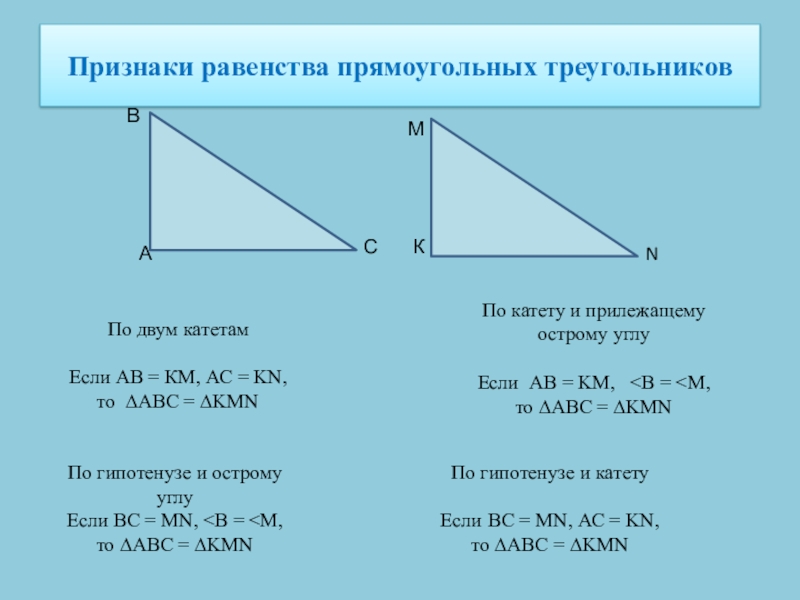
Слайд 7Признаки равенства прямоугольных треугольников
По двум катетам
Если АВ = КМ, АС =
то ∆АВС = ∆KMN
А
N
М
К
С
В
По катету и прилежащему острому углу
Если AB = KM, то ∆АВС = ∆KMN
По гипотенузе и острому углу
Если ВС = MN, то ∆АВС = ∆KMN
По гипотенузе и катету
Если ВС = МN, АС = KN,
то ∆АВС = ∆KMN
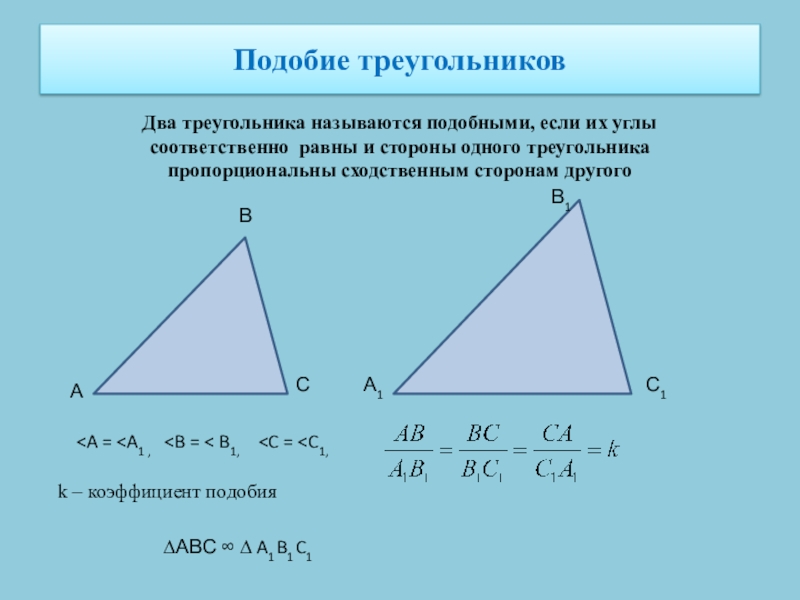
Слайд 8Подобие треугольников
Два треугольника называются подобными, если их углы соответственно равны и
А
С
В
В1
А1
С1
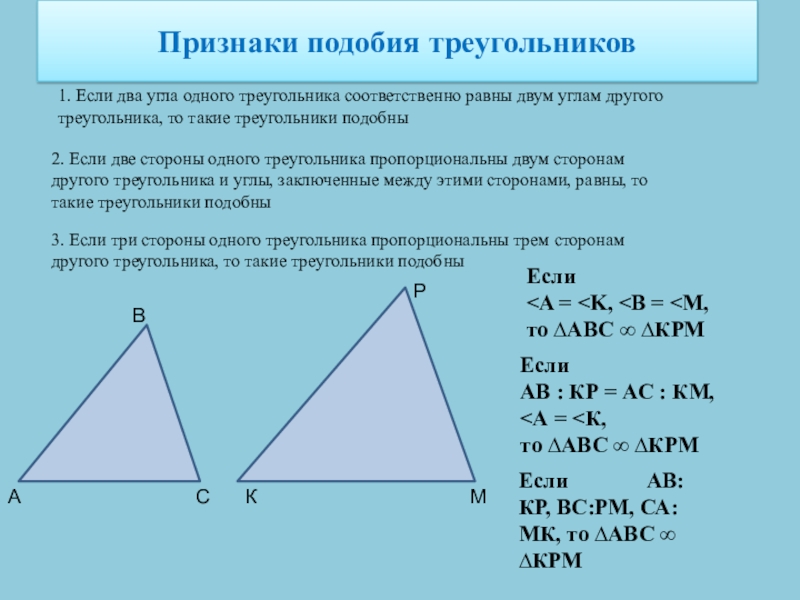
Слайд 9Признаки подобия треугольников
1. Если два угла одного треугольника соответственно равны двум
2. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны
3. Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны
А
В
С
К
М
Р
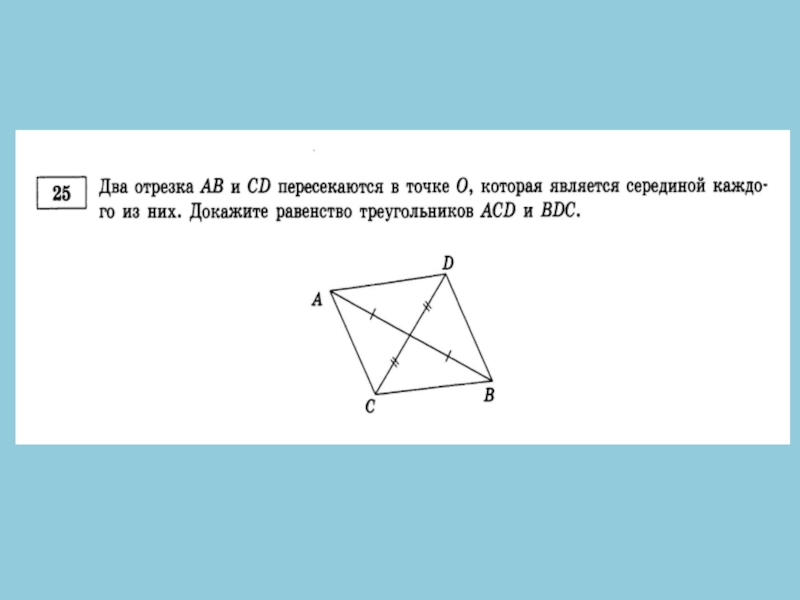
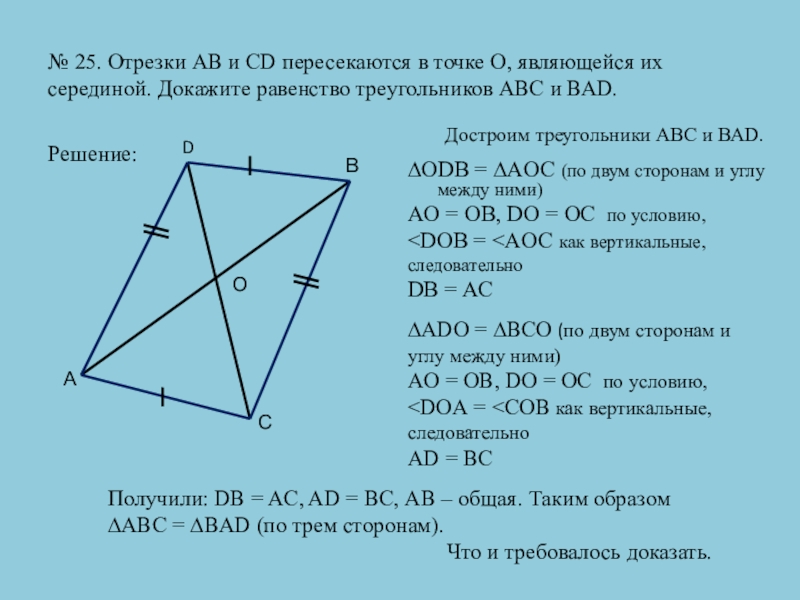
Слайд 18№ 25. Отрезки АВ и CD пересекаются в точке О, являющейся
Решение:
∆ODB = ∆AOC (по двум сторонам и углу между ними) А D С В О Достроим треугольники АВС и ВАD. ∆ADO = ∆BCO (по двум сторонам и углу между ними) Получили: DB = AC, AD = BC, АВ – общая. Таким образом
AO = OB, DO = OC по условию,
DB = AC
AO = OB, DO = OC по условию,
АD = ВC
∆ABC = ∆BAD (по трем сторонам).
Что и требовалось доказать.