- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Презентація з геометрії за темою Правильні многокутники. Існування вписаних і описаних кіл правильних многокутників. ( 9клас)
Содержание
- 1. Презентація з геометрії за темою Правильні многокутники. Існування вписаних і описаних кіл правильних многокутників. ( 9клас)
- 2. Мотивація вивчення темиМногокутники та його елементи. Опуклі
- 3. Аналіз контрольної роботиФормули площ трикутників, чотирикутників, паралелограма, трапеції, ромбаНаслідок з теореми косинусів
- 4. Задача №1Сторони трикутника дорівнюють 6см, 9 см і 13см. Знайдіть висоту, проведену до найменшої сторони.
- 5. Задача №2Сторони трикутника дорівнюють 7см, 11 см і 12см. Знайдіть медіану, проведену до найбільшої сторони.
- 6. Многокутник та його елементи. Опуклі та неопуклі многокутники. Сума кутів опуклого многокутника.
- 7. Актуалізація опорних знаньВиконання усних вправ
- 8. ЛаманаОзначення: Фігура, яка складається з точок А1,
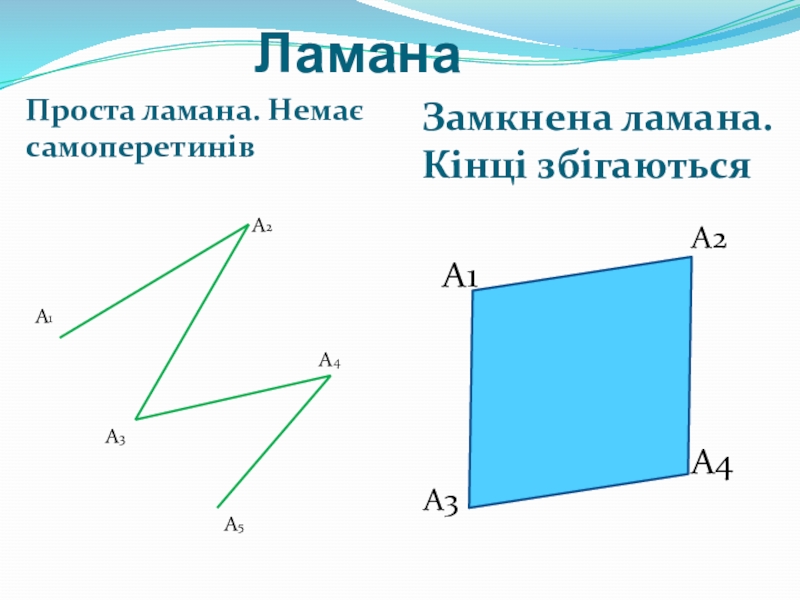
- 9. ЛаманаПроста ламана. Немає самоперетинівЗамкнена ламана. Кінці збігаютьсяА1А2А3А4А5А1А2А3А4
- 10. МногокутникОзначення. Замкнена проста ламана, сусідні ланки якої не лежать на одній прямій, називається многокутником.
- 11. Ланки ламаної називаються сторонами многокутника.
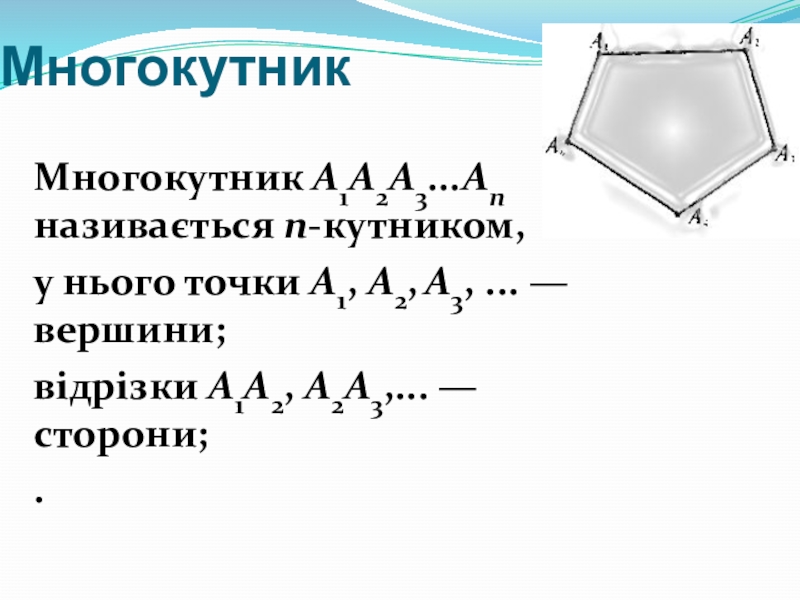
- 12. МногокутникМногокутник А1А2А3...Аn називається n-кутником, у нього точки
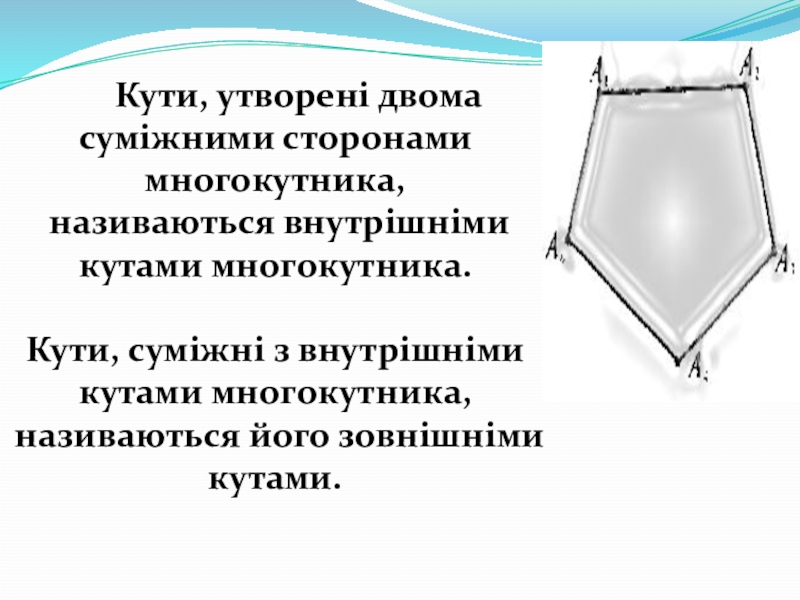
- 13. Кути, утворені
- 14. Слайд 14
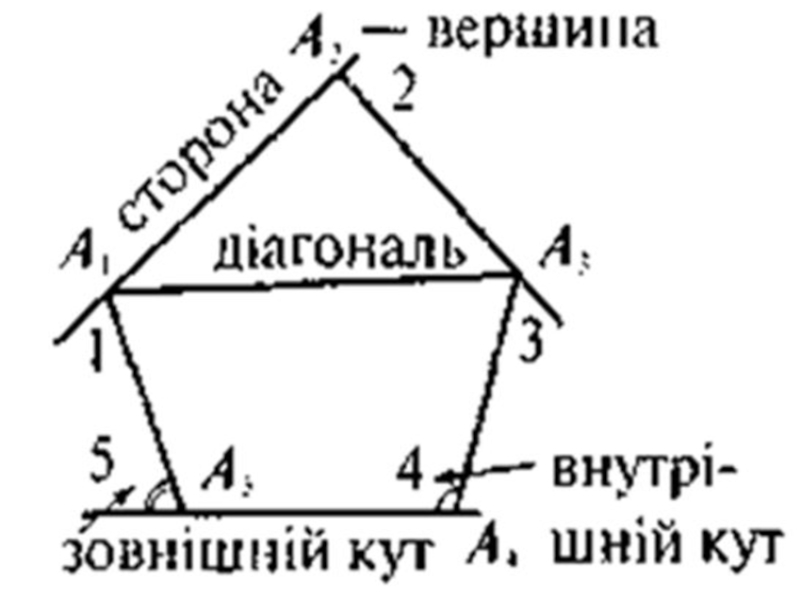
- 15. Відрізок, що з’єднує дві вершини,
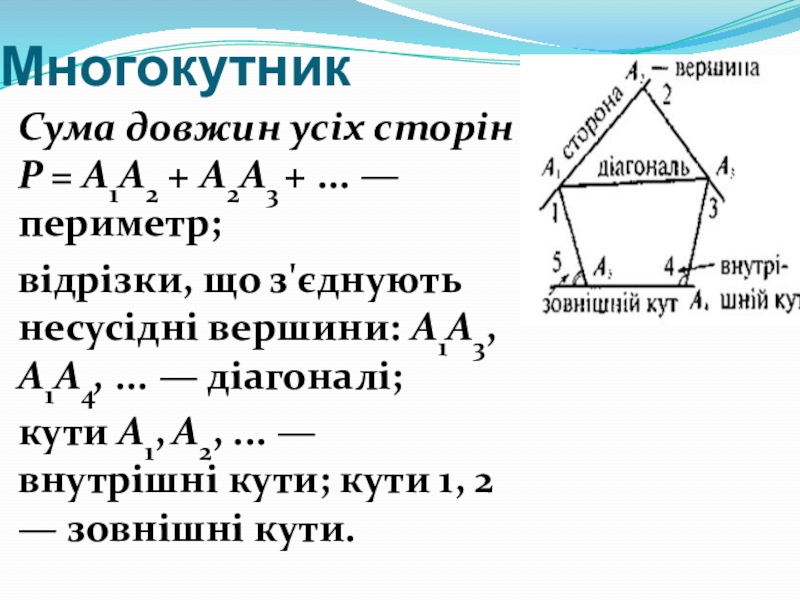
- 16. МногокутникСума довжин усіх сторін Р = А1А2
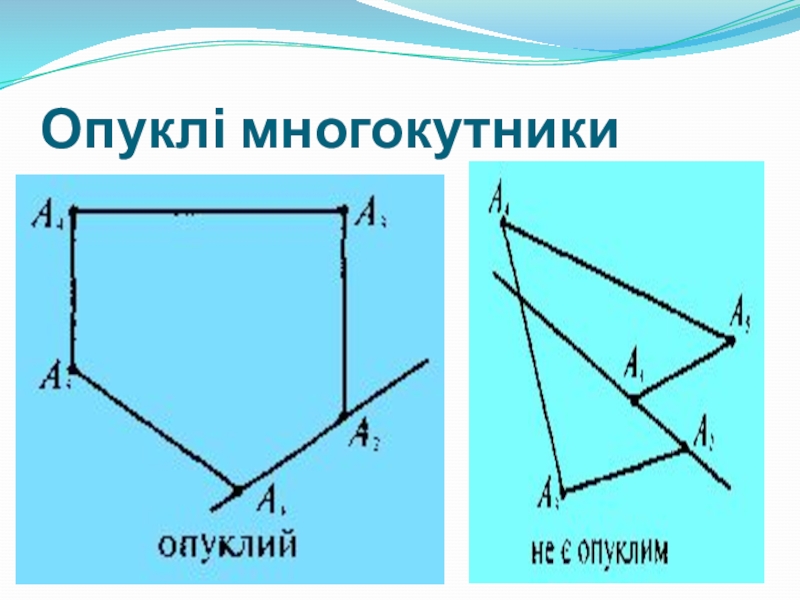
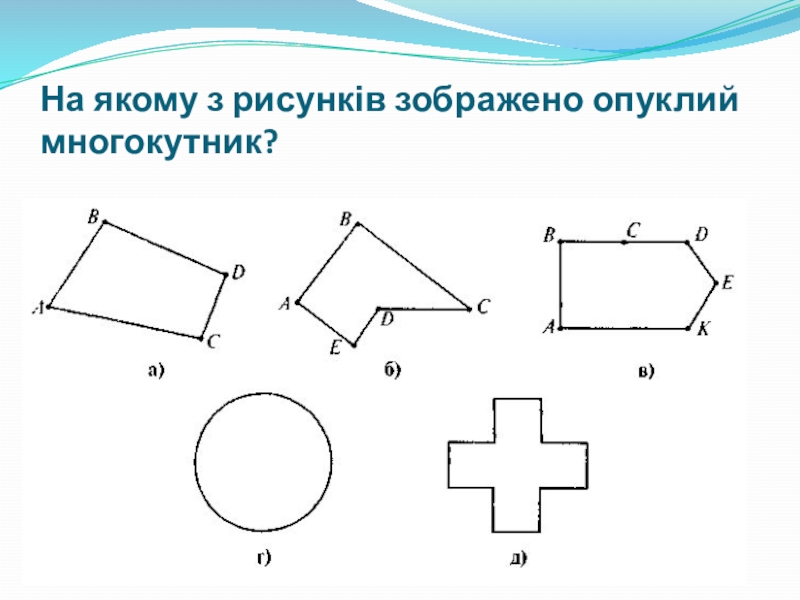
- 17. Многокутник називається опуклим, якщо він лежить в
- 18. Опуклі многокутники
- 19. Правильні многокутникиПравильним називається опуклий многокутник, в якого
- 20. Властивості (опуклих) многокутниківВ опуклому n-кутнику:1) із кожної
- 21. Властивості (опуклих) многокутників3) для будь-якої сторони а
- 22. Властивості (опуклих) многокутників6) якщо всі сторони і
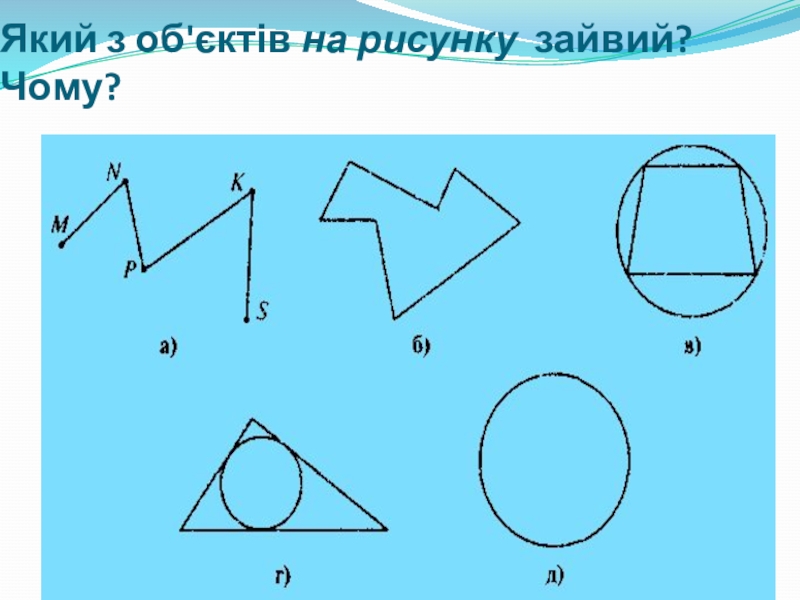
- 23. Чи можна вважати ламаними фігури, що зображені
- 24. На якому з рисунків зображено опуклий многокутник?
- 25. Усні вправи1). Скільки діагоналей виходить з однієї
- 26. Усні вправи3). Діагональ відтинає від п'ятикутника чотирикутник. Який вид має частина, що залишилася?
- 27. Тренувальні вправиВ опуклому п'ятикутнику ABCDE вершина В
- 28. Тренувальні вправиВ опуклому п'ятикутнику ABCDE вершина В
- 29. Який з об'єктів на рисунку зайвий? Чому?
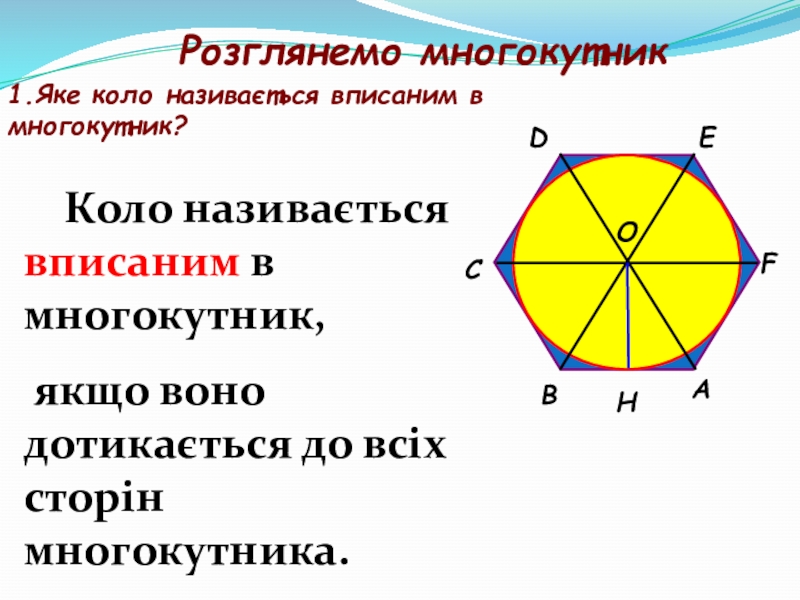
- 30. АВСDЕFОНРозглянемо многокутник1.Яке коло називається вписаним в многокутник? Коло
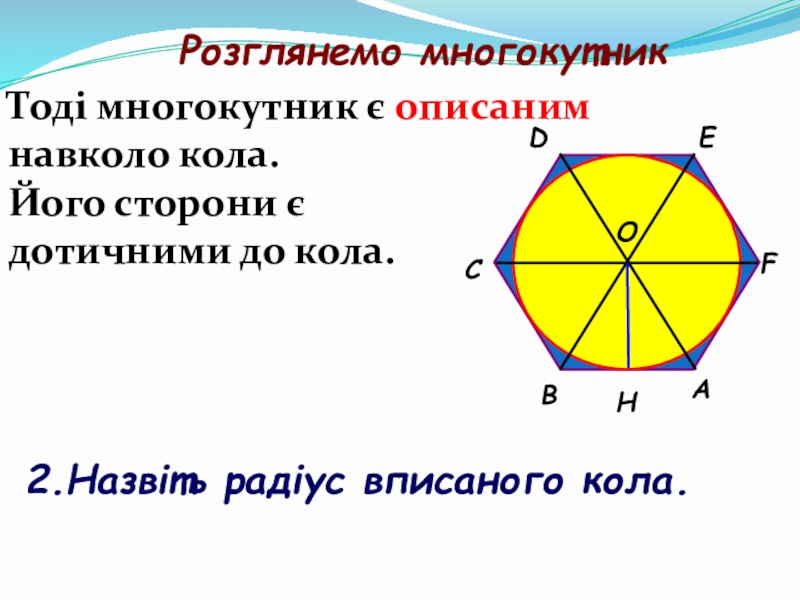
- 31. АВСDЕFОНРозглянемо многокутникТоді многокутник є описаним навколо кола.Його сторони є дотичними до кола.2.Назвіть радіус вписаного кола.
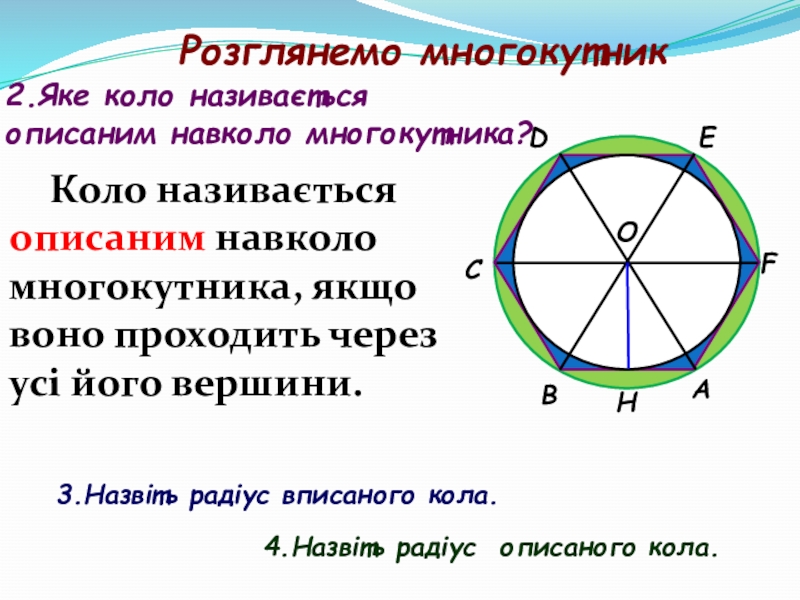
- 32. АВСDЕFОРозглянемо многокутник3.Яке коло називається описаним навколо многокутника?4.Назвіть
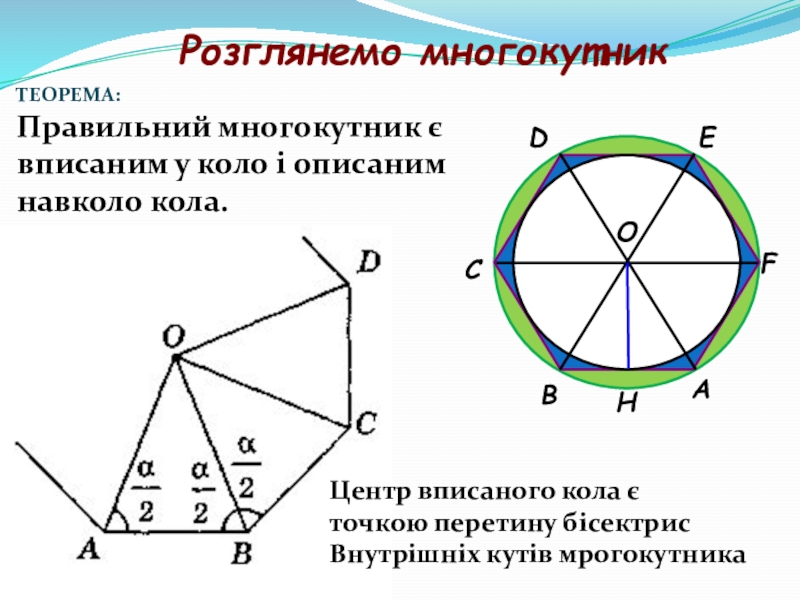
- 33. АВСDЕFОНРозглянемо многокутникТЕОРЕМА:Правильний многокутник є вписаним у коло
- 34. Доведення: НехайТочку перетину бісектрис кутів А і
- 35. Доведення:
- 36. Доведення:
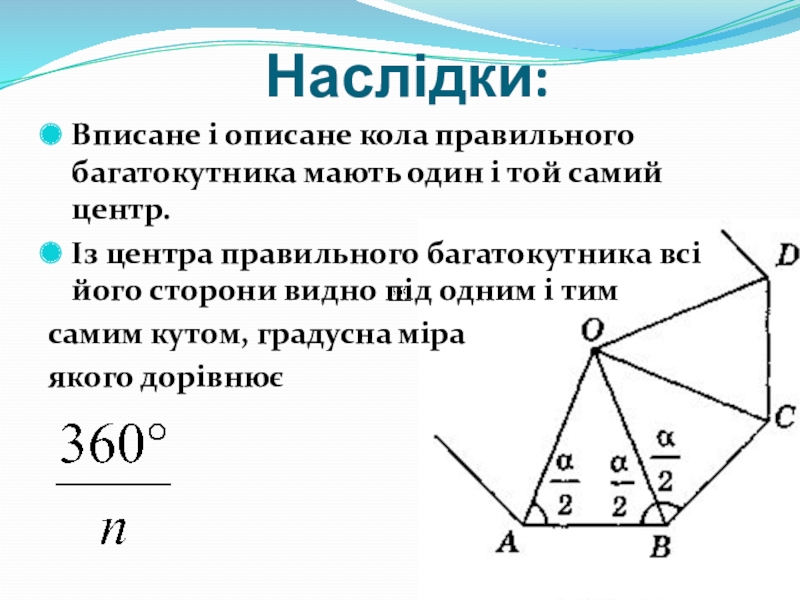
- 37. Наслідки:Вписане і описане кола правильного багатокутника мають
- 38. Робота з підручникомПідручник Г. АпостоловаСтор 94 Фронтально: №2(б), 4(а), 5(б)Робота в парах: №1(а), 3(а)
- 39. Підведення підсумківВИВЧИТИ п. 11, розв’язати: №№ 1(в), 4(в), 9(г), + 14(б)Домашнє завдання
- 40. Слайд 40
- 41. Слайд 41
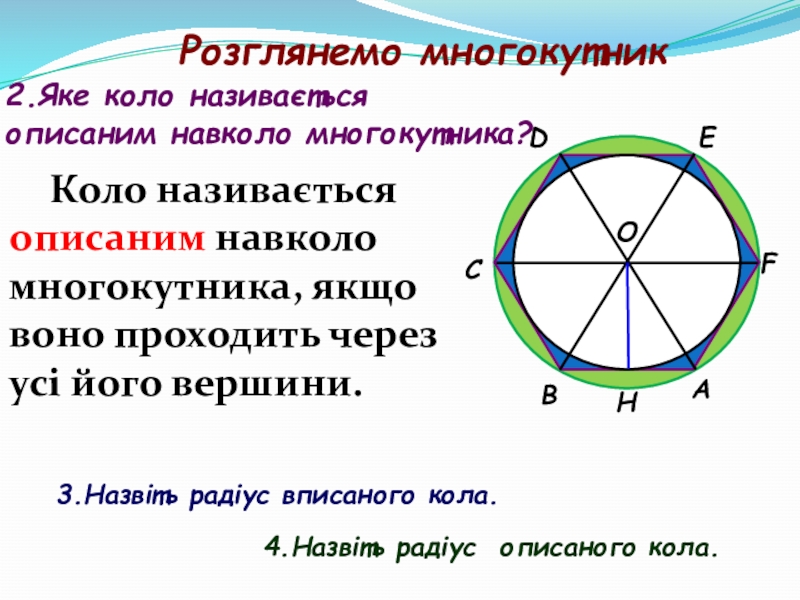
- 42. АВСDЕFОНРозглянемо многокутник2.Яке коло називається описаним навколо многокутника?3.Назвіть
- 43. АВСDЕFОНРозглянемо многокутник2.Яке коло називається описаним навколо многокутника?3.Назвіть
- 44. АВСDЕFОНРозглянемо многокутник2.Яке коло називається описаним навколо многокутника?3.Назвіть
Мотивація вивчення темиМногокутники та його елементи. Опуклі та неопуклі многокутникиСума кутів опуклого многокутникаПравильні многокутникиФормули для радіусів вписаних і описаних кіл правильних многокутників…Тематична контрольна робота
Слайд 1Сьоме листопада.
Класна робота
Означення правильних многокутників. Існування вписаного і описаного кіл
Слайд 2Мотивація вивчення теми
Многокутники та його елементи. Опуклі та неопуклі многокутники
Сума кутів
опуклого многокутника
Правильні многокутники
Формули для радіусів вписаних і описаних кіл правильних многокутників
…
Тематична контрольна робота
Правильні многокутники
Формули для радіусів вписаних і описаних кіл правильних многокутників
…
Тематична контрольна робота
Слайд 3Аналіз контрольної роботи
Формули площ трикутників, чотирикутників, паралелограма, трапеції, ромба
Наслідок з теореми
косинусів
Слайд 4Задача №1
Сторони трикутника дорівнюють 6см, 9 см і 13см. Знайдіть висоту,
проведену до найменшої сторони.
Слайд 5Задача №2
Сторони трикутника дорівнюють 7см, 11 см і 12см. Знайдіть медіану,
проведену до найбільшої сторони.
Слайд 6Многокутник та його елементи. Опуклі та неопуклі многокутники. Сума кутів опуклого
многокутника.
Слайд 8Ламана
Означення: Фігура, яка складається з точок А1, А2, ..., Аn, послідовно
сполучених відрізками, називається ламаною.
Ламана А1А2А3А4Аn:
точки А1, А2, А3.... — вершини ламаної; А1 і Аn — кінні ламаної; відрізки А1А2, А2А3.... — ланки ламаної.
Ламана А1А2А3А4Аn:
точки А1, А2, А3.... — вершини ламаної; А1 і Аn — кінні ламаної; відрізки А1А2, А2А3.... — ланки ламаної.
Слайд 10Многокутник
Означення. Замкнена проста ламана, сусідні ланки якої не лежать на одній
прямій, називається многокутником.
Слайд 11 Ланки ламаної називаються сторонами
многокутника.
Точки, в яких збігаються
дві суміжні ланки,
називаються вершинами многокутника.
називаються вершинами многокутника.
Слайд 12Многокутник
Многокутник А1А2А3...Аn називається n-кутником,
у нього точки А1, А2, А3, ...
— вершини;
відрізки А1А2, А2А3,... — сторони;
.
відрізки А1А2, А2А3,... — сторони;
.
Слайд 13
Кути, утворені двома суміжними сторонами
многокутника,
називаються внутрішніми кутами многокутника.
Кути, суміжні з внутрішніми кутами многокутника,
називаються його зовнішніми кутами.
називаються внутрішніми кутами многокутника.
Кути, суміжні з внутрішніми кутами многокутника,
називаються його зовнішніми кутами.
Слайд 15
Відрізок, що з’єднує дві вершини, які не належать
одній
з його сторін називається діагоналлю.
Сума довжин усіх сторін многокутника
називається його периметром.
Сума довжин усіх сторін многокутника
називається його периметром.
Слайд 16Многокутник
Сума довжин усіх сторін Р = А1А2 + А2А3 + ...
— периметр;
відрізки, що з'єднують несусідні вершини: А1А3, A1A4, ... — діагоналі;
кути А1, А2, ... — внутрішні кути; кути 1, 2 — зовнішні кути.
відрізки, що з'єднують несусідні вершини: А1А3, A1A4, ... — діагоналі;
кути А1, А2, ... — внутрішні кути; кути 1, 2 — зовнішні кути.
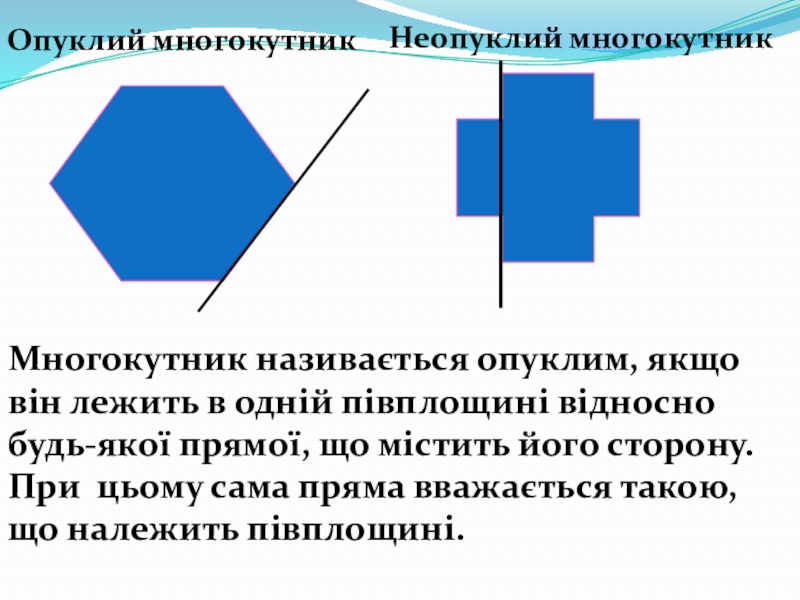
Слайд 17Многокутник називається опуклим, якщо він лежить в одній півплощині відносно будь-якої
прямої, що містить його сторону. При цьому сама пряма вважається такою, що належить півплощині.
Опуклий многокутник
Неопуклий многокутник
Слайд 19Правильні многокутники
Правильним називається опуклий многокутник, в якого всі кути і всі
сторони рівні.
Найпростіші приклади правильних многокутників є рівносторонній трикутник, квадрат.
Найпростіші приклади правильних многокутників є рівносторонній трикутник, квадрат.
Слайд 20Властивості (опуклих) многокутників
В опуклому n-кутнику:
1) із кожної вершини можна провести (n
– 3) діагоналі;
2) кількість усіх діагоналей дорівнює
2) кількість усіх діагоналей дорівнює
Слайд 21Властивості (опуклих) многокутників
3) для будь-якої сторони а справедливо, що а
Р (Р — периметр n-кутника);
4) сума внутрішніх кутів Sn = 180°(n – 2);
5) сума зовнішніх кутів, взятих по одному при кожній вершині — 360°;
4) сума внутрішніх кутів Sn = 180°(n – 2);
5) сума зовнішніх кутів, взятих по одному при кожній вершині — 360°;
Слайд 22Властивості (опуклих) многокутників
6) якщо всі сторони і всі кути рівні, то
n-кутник є правильним, і тоді
Р = аn,
(Р — периметр; а — сторона);
— внутрішній кут;
— зовнішній кут
Р = аn,
(Р — периметр; а — сторона);
— внутрішній кут;
— зовнішній кут
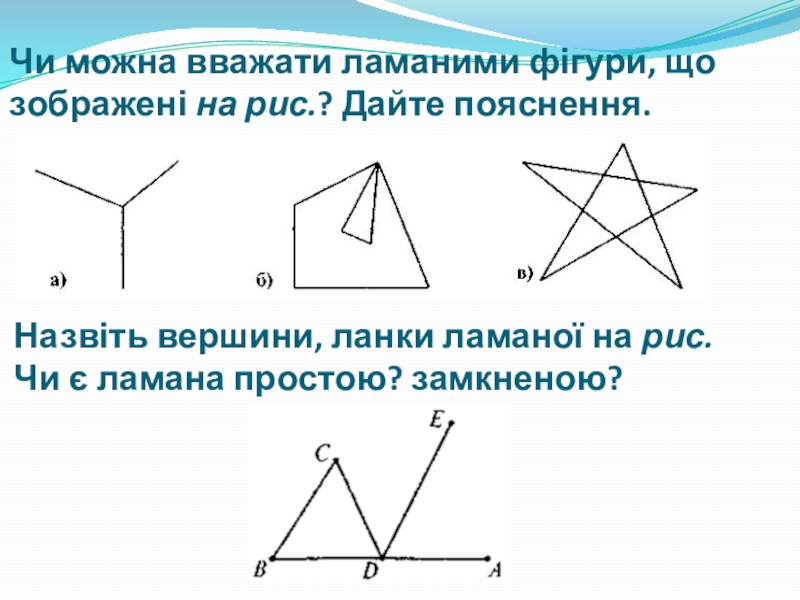
Слайд 23Чи можна вважати ламаними фігури, що зображені на рис.? Дайте пояснення.
Назвіть
вершини, ланки ламаної на рис. Чи є ламана простою? замкненою?
Слайд 25Усні вправи
1). Скільки діагоналей виходить з однієї вершини семикутника?
2). Чи може
діагональ шестикутника ділити його:
а) на два трикутники;
б) на два чотирикутники;
в) на трикутник і п'ятикутник?
а) на два трикутники;
б) на два чотирикутники;
в) на трикутник і п'ятикутник?
Слайд 26Усні вправи
3). Діагональ відтинає від п'ятикутника чотирикутник. Який вид має частина,
що залишилася?
Слайд 27Тренувальні вправи
В опуклому п'ятикутнику ABCDE вершина В з'єднана рівними діагоналями з
вершинами D і Е. Відомо, то ABE = CBD, BEA = BDC. Порівняйте периметри чотирикутників ABDE і BCDE.
Довжина будь-якої сторони многокутника менша від суми довжин решти сторін Доведіть.
Довжина будь-якої сторони многокутника менша від суми довжин решти сторін Доведіть.
Слайд 28Тренувальні вправи
В опуклому п'ятикутнику ABCDE вершина В з'єднана рівними діагоналями з
вершинами D і Е. Відомо, то ABE = CBD, BEA = BDC. Порівняйте периметри чотирикутників ABDE і BCDE.
Слайд 30А
В
С
D
Е
F
О
Н
Розглянемо многокутник
1.Яке коло називається вписаним в
многокутник?
Коло називається вписаним в многокутник,
якщо воно дотикається до всіх сторін многокутника.
Слайд 31А
В
С
D
Е
F
О
Н
Розглянемо многокутник
Тоді многокутник є описаним
навколо кола.
Його сторони є
дотичними до
кола.
2.Назвіть радіус вписаного кола.
Слайд 32А
В
С
D
Е
F
О
Розглянемо многокутник
3.Яке коло називається
описаним навколо многокутника?
4.Назвіть радіус описаного кола.
Коло називається
описаним навколо многокутника, якщо воно проходить через усі його вершини.
Тоді многокутник є вписаним у коло
Слайд 33А
В
С
D
Е
F
О
Н
Розглянемо многокутник
ТЕОРЕМА:
Правильний многокутник є вписаним у коло і описаним навколо кола.
Центр
вписаного кола є
точкою перетину бісектрис
Внутрішніх кутів мрогокутника
точкою перетину бісектрис
Внутрішніх кутів мрогокутника
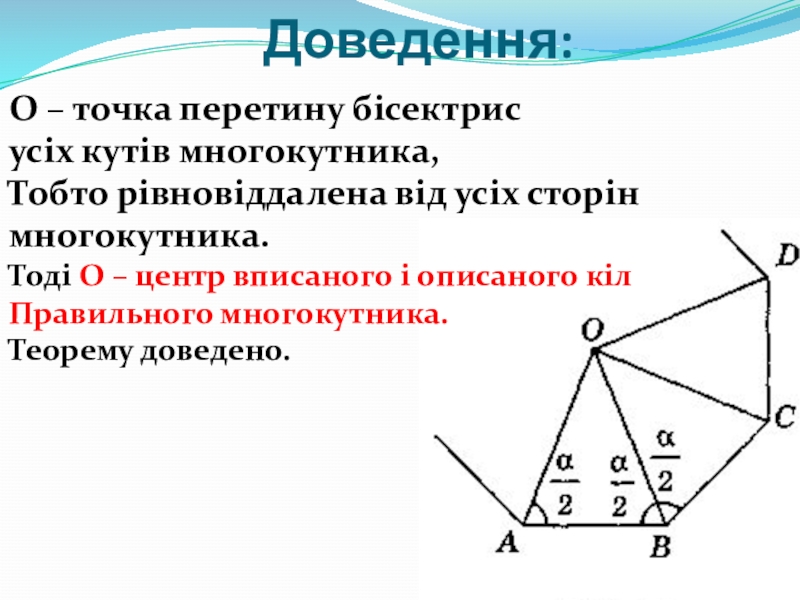
Слайд 34Доведення:
Нехай
Точку перетину бісектрис кутів А і В
позначимо через О. Тоді
з основою АВ.
ОА=ОВ як бічні сторони.
Слайд 35Доведення:
ОВ- спільна сторона для
тоді ці трикутники рівні за ІІ орт і
ОА=ОВ=ОС і
О-рівновіддалена
Від усіх вершин многокутника.
Слайд 36Доведення:
О – точка перетину бісектрис
усіх кутів многокутника,
Тобто рівновіддалена від усіх сторін
многокутника.
Тоді О – центр вписаного і описаного кіл
Правильного многокутника.
Теорему доведено.
Слайд 37Наслідки:
Вписане і описане кола правильного багатокутника мають один і той самий
центр.
Із центра правильного багатокутника всі його сторони видно під одним і тим
самим кутом, градусна міра
якого дорівнює
Із центра правильного багатокутника всі його сторони видно під одним і тим
самим кутом, градусна міра
якого дорівнює
Слайд 38Робота з підручником
Підручник Г. Апостолова
Стор 94
Фронтально: №2(б), 4(а), 5(б)
Робота в
парах: №1(а), 3(а)
Слайд 42А
В
С
D
Е
F
О
Н
Розглянемо многокутник
2.Яке коло називається
описаним навколо многокутника?
3.Назвіть радіус вписаного кола.
4.Назвіть радіус
описаного кола.
Коло називається описаним навколо многокутника, якщо воно проходить через усі його вершини.
Слайд 43А
В
С
D
Е
F
О
Н
Розглянемо многокутник
2.Яке коло називається
описаним навколо многокутника?
3.Назвіть радіус вписаного кола.
4.Назвіть радіус
описаного кола.
Коло називається описаним навколо многокутника, якщо воно проходить через усі його вершини.
Слайд 44А
В
С
D
Е
F
О
Н
Розглянемо многокутник
2.Яке коло називається
описаним навколо многокутника?
3.Назвіть радіус вписаного кола.
4.Назвіть радіус
описаного кола.
Коло називається описаним навколо многокутника, якщо воно проходить через усі його вершини.
