математики
Задорожною
Світланою Миколаївною
Гімназія № 3
м. Дніпропетровськ
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Презентація з геометрії для учнів 9 класу з теми: Відношення площ подібних многокутників
Содержание
- 1. Презентація з геометрії для учнів 9 класу з теми: Відношення площ подібних многокутників
- 2. Мета уроку:Ознайомити учнів з відношенням подібних многокутників,
- 3. Актуалізація опорних знань учнів Питання:Які трикутники
- 4. Дивовижні створіння ці мурахи! Звідки у
- 5. Припустимо, що в країні ліліпутів
- 6. Щоб дати відповідь на поставлені питання,
- 7. Завдання класу: заповніть пропуски у доведенні.А так як , то .
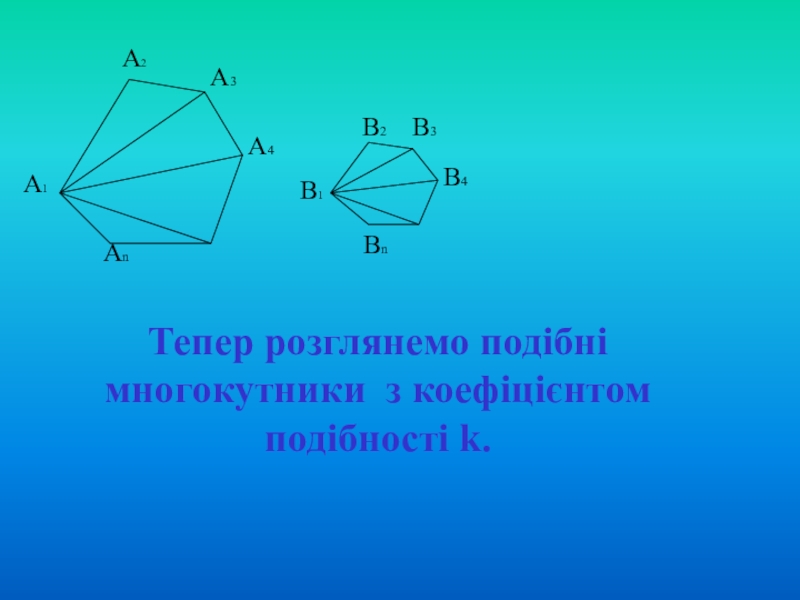
- 8. А1А2А3А4АnВ1В2В3В4ВnТепер розглянемо подібні многокутники з коефіцієнтом подібності k.
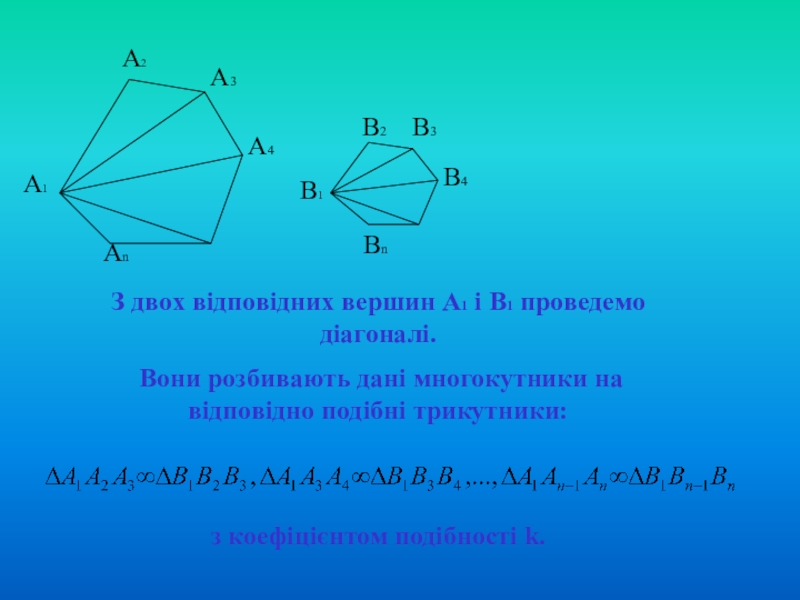
- 9. А1А2А3А4АnВ1В2В3В4ВnЗ двох відповідних вершин А1 і В1
- 10. .Тому маємо: Отже, Звідки Отже, ми довели теорему: „Відношення площ подібних многокутників дорівнює квадрату коефіцієнта подібності”.
- 11. Розв’язання задач за готовим рисунком:
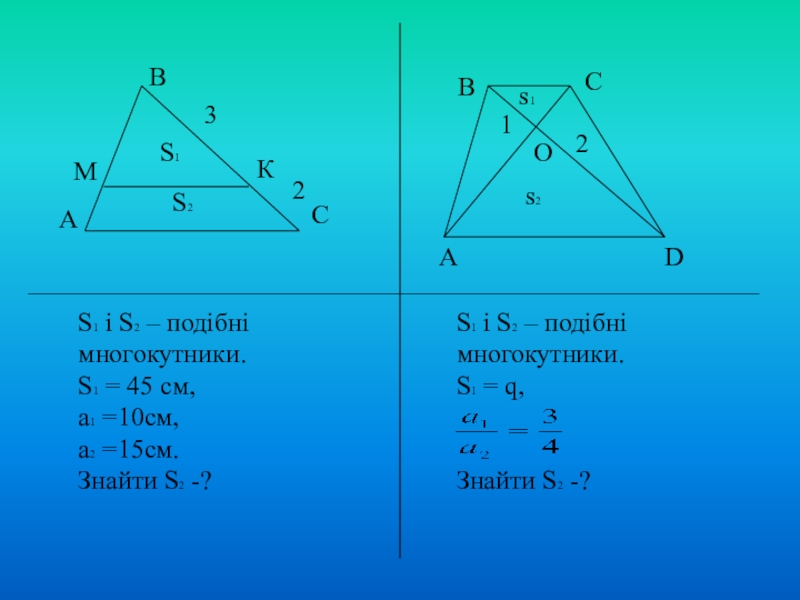
- 12. ВМАКСS1S232ABCDOs1s212S1 і S2 – подібнімногокутники.S1 = 45
- 13. Робота в групах
- 14. Задача № 1 (4 – 6 балів)
- 15. Розв’язання задачі № 1:Нехай S – площа
- 16. Задача № 2 ( 7 – 9
- 17. Розв’язання задачі № 2:У трикутниках АСН та
- 18. Задача № 3 ( 10 – 12
- 19. Розв’язання задачі № 3:Кожен з трикутників подібний
- 20. Тепер ми можемо отримати відповідь на ключове питання з початку уроку.Дамо відповідь на перше питання:
- 21. Уявимо собі, що пропорції людини в 100
- 22. Отже, в 144 рази більше
- 23. Підсумки урокуЩо нового ви узнали сьогодні на
Мета уроку:Ознайомити учнів з відношенням подібних многокутників, основними прийомами розв’язування задач на відношення подібних фігур. Вміти застосовувати набуті знання при розв’язанні задач різного рівня складності. Розвивати логічне мислення та уміння аналізувати, виділяти головне, узагальнювати набуті знання,
Слайд 2Мета уроку:
Ознайомити учнів з відношенням подібних многокутників, основними прийомами розв’язування задач
на відношення подібних фігур.
Вміти застосовувати набуті знання при розв’язанні задач різного рівня складності.
Розвивати логічне мислення та уміння аналізувати, виділяти головне, узагальнювати набуті знання, визначати та пояснювати поняття, ставити та розв’язувати проблеми.
Виховувати культуру математичної мови та алгоритмічного письма, гуманні відносини між учнями на уроці.
Вміти застосовувати набуті знання при розв’язанні задач різного рівня складності.
Розвивати логічне мислення та уміння аналізувати, виділяти головне, узагальнювати набуті знання, визначати та пояснювати поняття, ставити та розв’язувати проблеми.
Виховувати культуру математичної мови та алгоритмічного письма, гуманні відносини між учнями на уроці.
Слайд 3Актуалізація опорних
знань учнів
Питання:
Які трикутники називаються подібними?
2) Які многокутники називаються
подібними?
3) Які ознаки подібності ви знаєте?
4) Які формули для обчислення площ трикутників ви знаєте?
3) Які ознаки подібності ви знаєте?
4) Які формули для обчислення площ трикутників ви знаєте?
Слайд 4Дивовижні створіння ці мурахи!
Звідки у мурахи береться сила, щоб
тягти вантаж у десять раз важче його самого?
Людина не може, наприклад, піднятися сходами, тримаючи на собі піаніно!!!
Виходить, що мураха відносно сильніше за людину!
Слайд 5Припустимо, що в країні ліліпутів всі люди, будівлі, витвори
природи в 12 раз менше, ніж нормальні виміри, а в країні велитнів – у стільки ж раз більше.
Тоді спробуємо відповісти на питання:
В скільки раз Гуліверу потрібно більше тканини на костюм, ніж ліліпутам?
Слайд 6 Щоб дати відповідь на поставлені питання, треба з’ясувати, як відносяться
площі подібних многокутників?
Розглянемо спочатку подібні трикутники. Нехай трикутники АВС і КЕМ – подібні.
Тоді
АС:КМ= АВ:КЕ = ВС:ЕМ = k.
А
В
С
К
Е
М
Розглянемо відношення площ цих трикутників.
Слайд 9А1
А2
А3
А4
Аn
В1
В2
В3
В4
Вn
З двох відповідних вершин А1 і В1 проведемо діагоналі.
Вони розбивають
дані многокутники на відповідно подібні трикутники:
з коефіцієнтом подібності k.
Слайд 10.
Тому маємо:
Отже,
Звідки
Отже, ми довели теорему: „Відношення площ подібних
многокутників дорівнює квадрату коефіцієнта подібності”.
Слайд 12В
М
А
К
С
S1
S2
3
2
A
B
C
D
O
s1
s2
1
2
S1 і S2 – подібні
многокутники.
S1 = 45 cм,
а1 =10см,
а2 =15см.
Знайти S2
-?
S1 і S2 – подібні
многокутники.
S1 = q,
Знайти S2 -?
Слайд 14Задача № 1 (4 – 6 балів)
Периметри подібних многокутників відносяться
як 5:7, а різниця площ дорівнює 864.
Знайдіть площі многокутників.
Знайдіть площі многокутників.
Слайд 15Розв’язання задачі № 1:
Нехай S – площа меншого многокутника,
тоді S
+ 864 – площа більшого многокутника.
Маємо пропорцію:
24 S = 21600, S = 900.
Тоді, S + 864 = 1764.
Відповідь: 1764.
Слайд 16Задача № 2 ( 7 – 9 балів)
Висота, що проведена
до гіпотенузи прямокутного трикутника, ділить його на два трикутники, площі яких 6см та 54см.
Знайдіть гіпотенузу.
Знайдіть гіпотенузу.
Слайд 17Розв’язання задачі № 2:
У трикутниках АСН та ВСН, кут САН
дорівнює
куту НСВ,
тому трикутники АСН та ВСН – подібні
за двома кутами.
тому трикутники АСН та ВСН – подібні
за двома кутами.
З подібності трикутників слідує, що
Отже, нехай х – коефіцієнт пропорційності, тоді АС = 3х см, ВС = х см, а за теоремою Піфагора: АВ = х
1,5 х2 = 60, х2 = 40, АВ = 20см.
Відповідь: 20 см.
Слайд 18Задача № 3 ( 10 – 12 балів)
Через точку М,
що розташована усередині трикутника АВС, проведені прямі, паралельні сторонам трикутника. Вони розбивають трикутник на шість частин, три з яких – трикутники. Площі цих трикутників відомі – S1, S2, S3 .
Обчислити площу S даного трикутника.
Обчислити площу S даного трикутника.
Слайд 19Розв’язання задачі № 3:
Кожен з трикутників подібний
даному за двома кутами.
PBLM – паралелограм, тому PM = BL. З подібності випливає, що
Аналогічно,
Добуваючи з обох частин всіх трьох рівностей квадратні корені
та додаючи отримані рівності, отримаємо:
Так як BL + LN + NC = BC, то отримаємо:
.
Слайд 20Тепер ми можемо отримати відповідь на ключове питання з початку уроку.
Дамо
відповідь
на
перше питання:
на
перше питання:
Слайд 21Уявимо собі, що пропорції людини в 100 раз більше, ніж пропорції
мурахи.
Тоді у людини об’єм і вага всього тіла, а також кожного з його органів
буде в 100 000 000 раз більше.
Всі ж відповідні площинні виміри, в тому числі і поперечний переріз м’язів, лише в
100 000 раз більше.
Тобто, людина стала відносно в 100 раз слабше…
Слайд 22Отже, в 144 рази більше тканини потрібно Гулліверу, ніж
ліліпуту.
Дамо відповідь на друге питання:
Поверхня тіла Гуллівера більше, ніж у ліліпута в
12 * 12 = 144 раза
Слайд 23Підсумки уроку
Що нового ви узнали сьогодні на уроці?
З яким утрудненням
виведена теорема
допомогла справитися?
допомогла справитися?
Чому ми училися на уроці?
