- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад адачи по стереометрии ЕГЭ
Содержание
- 1. ПрезентацияЗадачи по стереометрии ЕГЭ
- 2. Запомни!
- 3. Слайд 3
- 4. Объем куба равен 8. Найдите площадь его
- 5. Найдите обьем многогранника, изображенного на рисунке (все двугранные углы многогранника прямые) Vцелого =5∙2∙4=40параллелепипедаVудалённного=2∙2∙1=4параллелепипедаVмногогранника=40-4=36Ответ:36
- 6. Два ребра прямоугольного параллелепипеда, выходящие из одной
- 7. Во сколько раз увеличится объем куба, если
- 8. Во сколько раз увеличится площадь поверхности куба,
- 9. Найдите боковое ребро правильной четырехугольной призмы, если
- 10. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые). 2∙1∙7+2∙1∙5+2∙5∙7-2∙1∙2+2∙1∙1+2∙1∙2=14+10+70-4+2+4=96Ответ: 96
- 11. Найдите объем многогранника, изображенного на рисунке (все
- 12. Два ребра прямоугольного параллелепипеда, выходящие из одной
- 13. Два ребра прямоугольного параллелепипеда, выходящие из
- 14. Два ребра прямоугольного параллелепипеда, выходящие из одной
- 15. Два ребра прямоугольного параллелепипеда, выходящие из одной
- 16. Найдите площадь поверхности многогранника, изображенного на
- 17. Площадь поверхности куба равна 18. Найдите его
- 18. Площадь поверхности куба равна 96. Найдите его объем. Пусть ребро куба –х6х2 =96х2=16х=44-ребро кубаОтвет:64
- 19. Найдите площадь поверхности прямой призмы, в основании
- 20. Если каждое ребро куба увеличить на 1,
- 21. Объем куба равен 8. Найдите площадь его
- 22. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые 5-3=2 высота нижнего параллелепипеда5∙4∙2+3∙4∙3=40+36=76Ответ76
- 23. Диагональ куба равна 1. Найдите площадь его
- 24. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые)5∙2∙6-1∙3∙2=60-6=54Ответ:54
- 25. Найдите площадь боковой поверхности правильной шестиугольной
- 26. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые 5∙3∙3+5∙4∙3+3∙1∙3=45+60+9=114Ответ:114
- 27. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые) 2∙3∙3+2∙2∙2+5∙2+2∙3+2∙2+2∙3+2∙2+2∙1=18+8+10+6+4+6+4+2=58Ответ:58
- 28. Спасибо за внимание!!!
Слайд 4Объем куба равен 8. Найдите площадь его поверхности
Пусть ребро куба а.
V=a3
a3=8
а=2
Площадь поверхности S=6a2
S=6∙22=24
Ответ:24
Слайд 5Найдите обьем многогранника, изображенного на рисунке (все двугранные углы
многогранника прямые)
Vцелого =5∙2∙4=40
параллелепипеда
Vудалённного=2∙2∙1=4
параллелепипеда
Vмногогранника=40-4=36
Ответ:36
Слайд 6Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 3 и
Пусть третье ребро х
2∙3∙4+2х∙4+2х∙3=94
24+8х+6х=94
14х=70
х=70:14
х=5
Ответ:5
Слайд 7Во сколько раз увеличится объем куба, если его ребра увеличить в
Пусть ребро куба х ,тогда объём куба х3
Объём куба после увеличения ребра (3х)3=27х3
-во столько раз увеличится объем куба, если его ребра увеличить в три раза
Ответ: 27
Найдите объем многогранника, изображенного на рисунке
(все двугранные углы прямые
4∙3∙5=60-объём параллелепипеда
2∙2∙1=4- объём параллелепипеда, который вырезали
60-4=56
Ответ:56
Слайд 8Во сколько раз увеличится площадь поверхности куба, если его ребро увеличить
Пусть х- ребро куба
6
- площадь поверхности куба
6(3х)
=6∙9∙
=54
площадь поверхности нового куба
=9 - во столько раз увеличится площадь поверхности куба
Ответ: 9
Слайд 9Найдите боковое ребро правильной четырехугольной призмы, если сторона ее основания равна
Пусть х-боковое ребро
2∙20∙20+2х∙20+2х∙20=1760
800+40х+40х=1760
80х=960
х=12
Ответ:12
Слайд 10Найдите площадь поверхности многогранника, изображенного
на рисунке (все двугранные углы прямые).
2∙1∙7+2∙1∙5+2∙5∙7-2∙1∙2+2∙1∙1+2∙1∙2=14+10+70-4+2+4=96
Ответ:
Слайд 11Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые
3∙1∙4=12 объём
1∙3∙1=3- объём верхнего параллелепипеда
12+3=15 объем многогранника
Ответ:15
Слайд 12Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 2.
Пусть х ребро параллелепипеда
2∙1∙2+2∙х∙1+2х∙2=16
4+2х+4х=16
6х=12
х=2
=
d>0,d=3
Ответ:3
Слайд 13Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 4 и
Пусть х- ребро параллелепипеда
48х=144
х=3
169 d=13
Ответ:13
Слайд 14Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 42 и
3364=1764+576+х2
х2=1024
х=32
Площадь поверхности параллелепипеда
2∙42∙24+2∙42∙32+2∙24∙32=2016+2688+1536==6240
Ответ:6240
Слайд 15Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 6 и
Пусть ребро параллелепипеда х
х2=9
х=3
=108
Ответ:108
Слайд 16Найдите площадь поверхности многогранника, изображенного
на рисунке (все двугранные углы прямые)
5-3=2
2∙2∙5+2∙2∙5+5∙5+2∙3∙3+2∙3∙3+3∙3+(5∙5-3∙3)=126-
площадь поверхности многогранника
Ответ:126
Слайд 17Площадь поверхности куба равна 18. Найдите его диагональ
Пусть х –ребро куба
Площадь
х2=3
Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений
=3∙3=9
d=
Ответ :3
Слайд 18Площадь поверхности куба равна 96. Найдите его объем.
Пусть ребро куба –х
6х2
х2=16
х=4
4-ребро куба
Ответ:64
Слайд 19Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с
=
24
Сторона ромба
=
=5
5∙4∙10=200
Ответ: 248
Слайд 20Если каждое ребро куба увеличить на 1, то его площадь поверхности
Пусть х- ребро куба
х2 - площадь одной грани
6х2- площадь поверхности куба
После изменения х+1 - ребро куба
(х+1)2 - площадь одной грани
6(х+1)2- площадь поверхности куба
6(х+1)2-6х2=30
6х2+12х+6-6х2=30
12х=24
х=2
2- ребро куба
Ответ:2
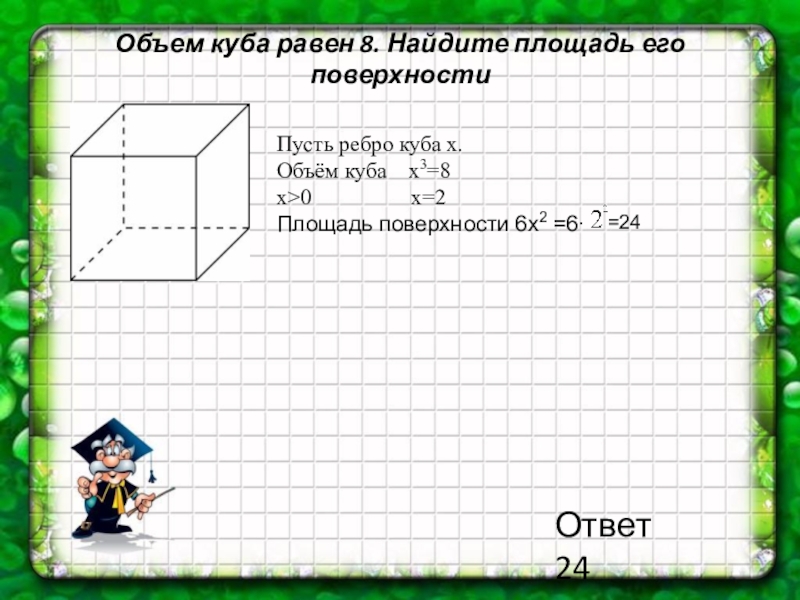
Слайд 21Объем куба равен 8. Найдите площадь его поверхности
Пусть ребро куба х.
Объём
x>0 x=2
Площадь поверхности 6х2 =6∙
=24
Ответ 24
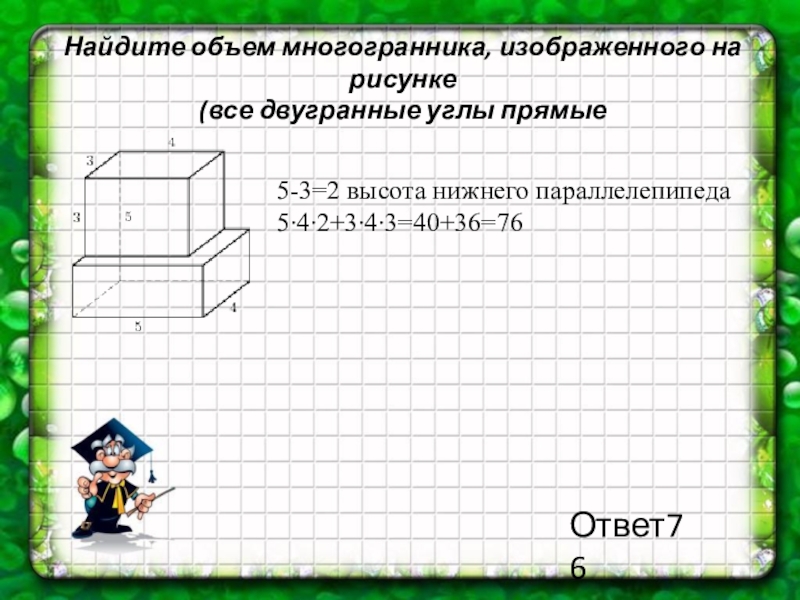
Слайд 22Найдите объем многогранника, изображенного на рисунке
(все двугранные углы прямые
5-3=2 высота
5∙4∙2+3∙4∙3=40+36=76
Ответ76
Слайд 23Диагональ куба равна 1. Найдите площадь его поверхности
Квадрат диагонали прямоугольного параллелепипеда
Пусть х-ребро куба
12 =х2+х2+х2
3х2=1
х2=
Площадь его поверхности 6х2=6∙
=2
Ответ:2
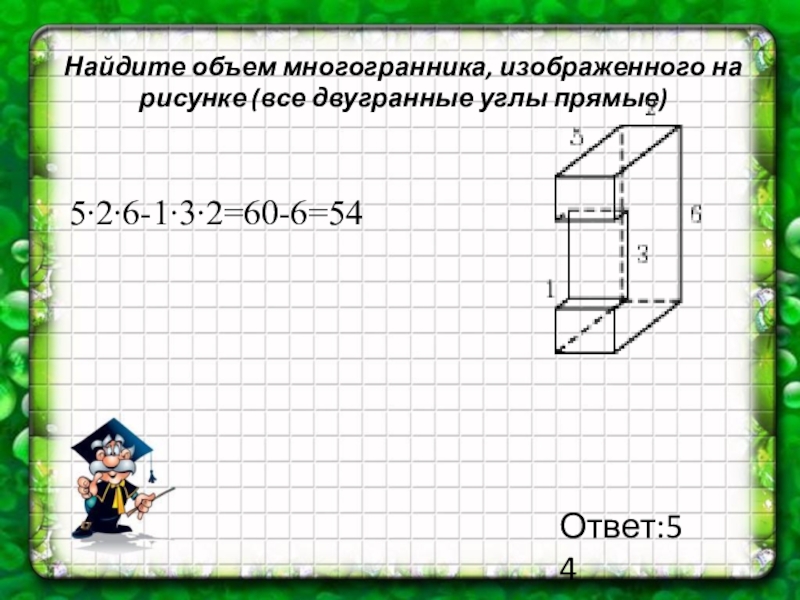
Слайд 24Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые)
5∙2∙6-1∙3∙2=60-6=54
Ответ:54
Слайд 25Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна
Ответ: 300
Слайд 26Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые
5∙3∙3+5∙4∙3+3∙1∙3=45+60+9=114
Ответ:114
Слайд 27Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые)
2∙3∙3+2∙2∙2+5∙2+2∙3+2∙2+2∙3+2∙2+2∙1=18+8+10+6+4+6+4+2=58
Ответ:58
