- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад задач по планиметрии второй части профильного ЕГЭ (С4)
Содержание
- 1. Презентация задач по планиметрии второй части профильного ЕГЭ (С4)
- 2. СодержаниеЗадача 1Задача 2Задача 3Задача 4Задача 5Задача 6Задача
- 3. 1. В прямоугольном треугольнике ABC гипотенуза АВ
- 4. 2. В треугольнике ABC проведена медиана BM.
- 5. 3. В выпуклом четырёхугольнике ABCD отрезки, соединяющие
- 6. 4. Найдите площадь трапеции с основаниями 18
- 7. 5. Две стороны треугольника равны З и
- 8. 6. Отношение отрезковТочки M и
- 9. Решение:1.Пусть продолжения BN и AD пересекаются в
- 10. 7. Отношение площадей.В треугольнике ABC медиана AD
- 11. Решение:1) ABD равнобедренный, так как
- 12. 8. Касательная к окружностиИз точки M, лежащей
- 13. Решение:1) Пусть K – точка пересечения окружности
- 14. 9. Касающиеся окружностиОкружности с центрами
- 15. Решение:1) Проведём общую касательную из точки C
- 16. 10. Задача. На катетах прямоугольного треугольника, как
- 17. 11. Задача. Найдите радиусы вписанной и описанной
- 18. Радиус окружности, вписанной в
- 19. Пропорциональные отрезки в окружности Теорема.
- 20. Рассмотрим ещё один пример. Пример 2. Докажите,
- 21. 12. Задача. На продолжении диаметра АВ окружности
- 22. 13. Задача. Окружность S1 проходит через центр
- 23. 14. Задача. На стороне АВ треугольника АВС
- 24. 15. Задача. Углы при вершинах A и
Слайд 2Содержание
Задача 1
Задача 2
Задача 3
Задача 4
Задача 5
Задача 6
Задача 7
Задача 8
Задача 9
Задача 10
Задача
Задача 12Задача 12 Задача 12 (теорема)
Задача 13
Задача 14
Задача15
Слайд 31. В прямоугольном треугольнике ABC гипотенуза АВ равна c и ∠ABC=α.Найдите
Р е ш е н и е. Поскольку медиана прямоугольного треугольника, проведённая из вершины прямого угла, равна половине гипотенузы, медиана CM равна .
Пусть K– середина BC.Тогда CK= BC= AB*cosα= *c*cos α.По теореме Пифагора из прямоугольного треугольника ACK находим, что
AK= = =
= = =
=
Аналогично находим медиану BN.
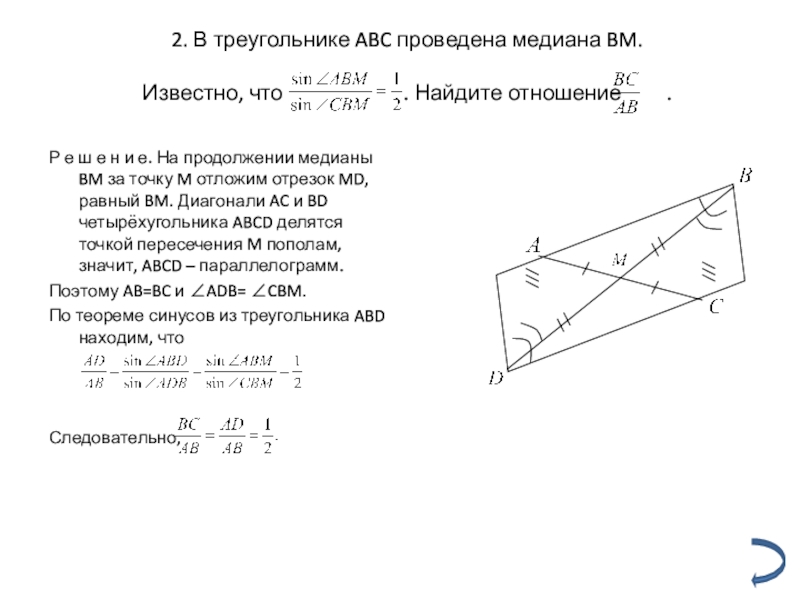
Слайд 42. В треугольнике ABC проведена медиана BM. Известно, что
Р е ш е н и е. На продолжении медианы BM за точку M отложим отрезок MD, равный BM. Диагонали AC и BD четырёхугольника ABCD делятся точкой пересечения M пополам, значит, ABCD – параллелограмм.
Поэтому AB=BC и ∠ADB= ∠CBM.
По теореме синусов из треугольника ABD находим, что
Следовательно,
Слайд 53. В выпуклом четырёхугольнике ABCD отрезки, соединяющие середины противоположных сторон, пересекаются
Р е ш е н и е. Середины сторон любого четырёхугольника являются вершинами параллелограмма, стороны которого параллельны диагоналям четырёхугольника и соответственно равны их половинам.
Обозначим через x и 3x половины диагоналей параллелограмма. Поскольку угол между ними равен 60˚, то по теореме косинусов квадраты сторон параллелограмма равны
x²+9x²-3x²=7x² , x²+9x²+3x²=13x²
Поскольку большая диагональ четырёхугольника равна , большая сторона параллелограмма равна ,
т. е. 13х²= , откуда x= . Тогда
меньшая сторона параллелограмма
равна . Следовательно, меньшая диагональ данного четырёхугольника равна
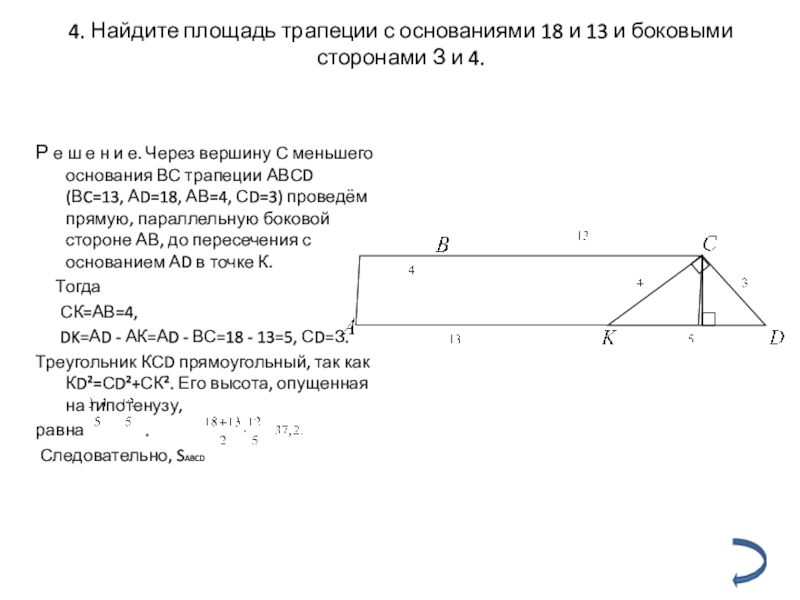
Слайд 64. Найдите площадь трапеции с основаниями 18 и 13 и боковыми
Р е ш е н и е. Через вершину С меньшего основания ВС трапеции АВСD (ВC=13, АD=18, АВ=4, СD=3) проведём прямую, параллельную боковой стороне АВ, до пересечения с основанием АD в точке К.
Тогда
СК=АВ=4,
DK=АD - АК=АD - ВС=18 - 13=5, СD=З.
Треугольник КСD прямоугольный, так как КD²=СD²+СК². Его высота, опущенная на гипотенузу,
равна .
Следовательно, SABCD
Слайд 75. Две стороны треугольника равны З и 6, а угол между
Решение. Пусть АD — биссектриса треугольника АВС, в котором АВ =6, АС =3, ∠ВАС=60°.
Первый способ. Обозначим AD=x. Тогда
SABC=
SABC=SABC+SACD=
=
Из уравнения находим, что x=2
Второй способ. Заметим, что треугольник АВС прямоугольный. Тогда треугольник ACD также прямоугольный, причём САD =30°. Следовательно,
AD=AC:cos∠CAD=3:cos30°=2
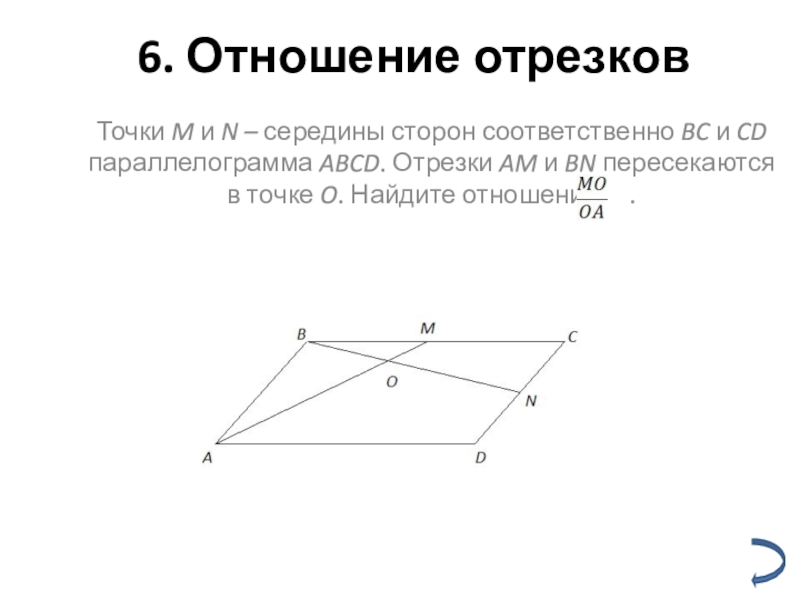
Слайд 8 6. Отношение отрезков
Точки M и N – середины сторон
Слайд 9
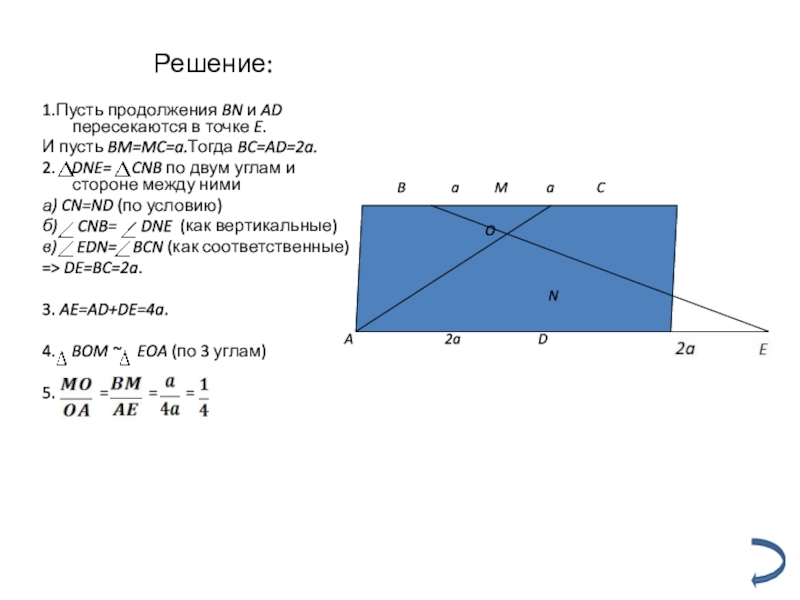
Решение:
1.Пусть продолжения BN и AD пересекаются в точке E.
И пусть
2. DNE= CNB по двум углам и стороне между ними
а) CN=ND (по условию)
б) CNB= DNE (как вертикальные)
в) EDN= BCN (как соответственные)
=> DE=BC=2a.
3. AE=AD+DE=4a.
4. BOM ~ EOA (по 3 углам)
5. = = =
B a M a C
O
N
A 2a D
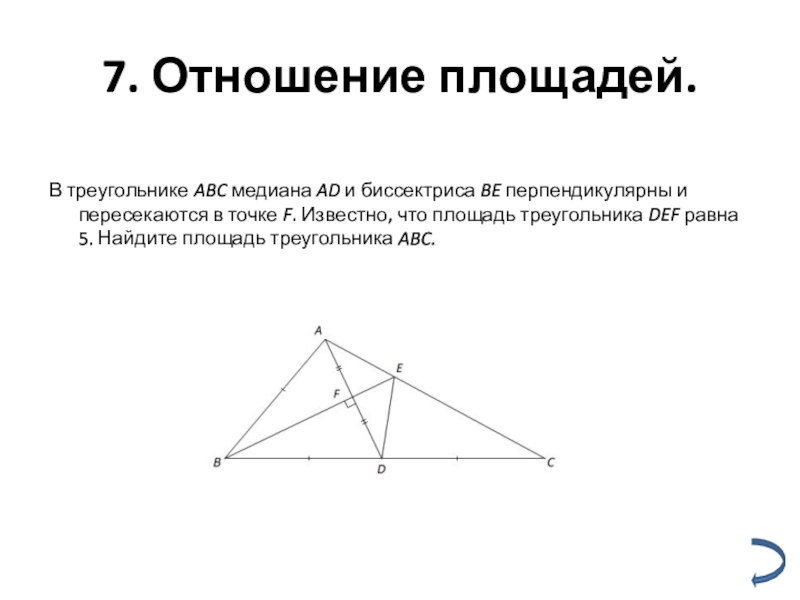
Слайд 107. Отношение площадей.
В треугольнике ABC медиана AD и биссектриса BE перпендикулярны
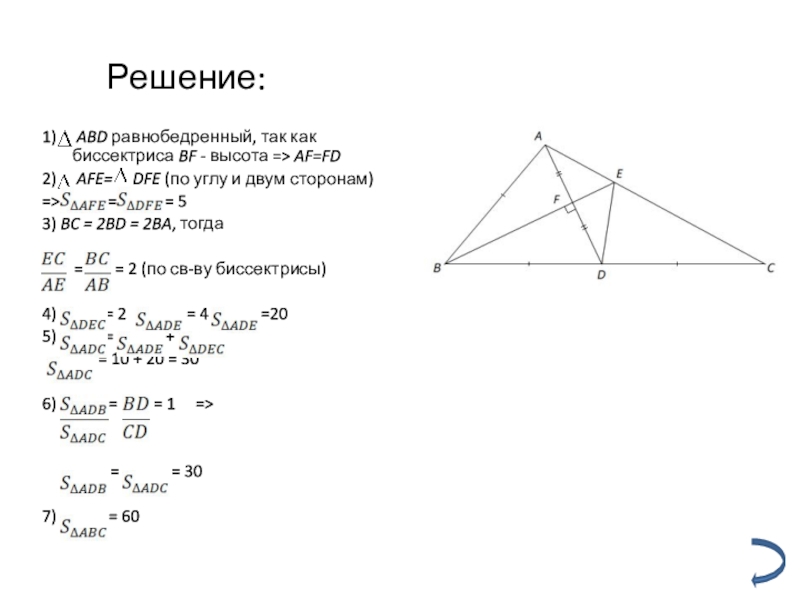
Слайд 11Решение:
1) ABD равнобедренный, так как биссектриса BF - высота
2) AFE= DFE (по углу и двум сторонам)
=> = = 5
3) BC = 2BD = 2BA, тогда
= = 2 (по св-ву биссектрисы)
4) = 2 = 4 =20
5) = +
= 10 + 20 = 30
6) = = 1 =>
= = 30
7) = 60
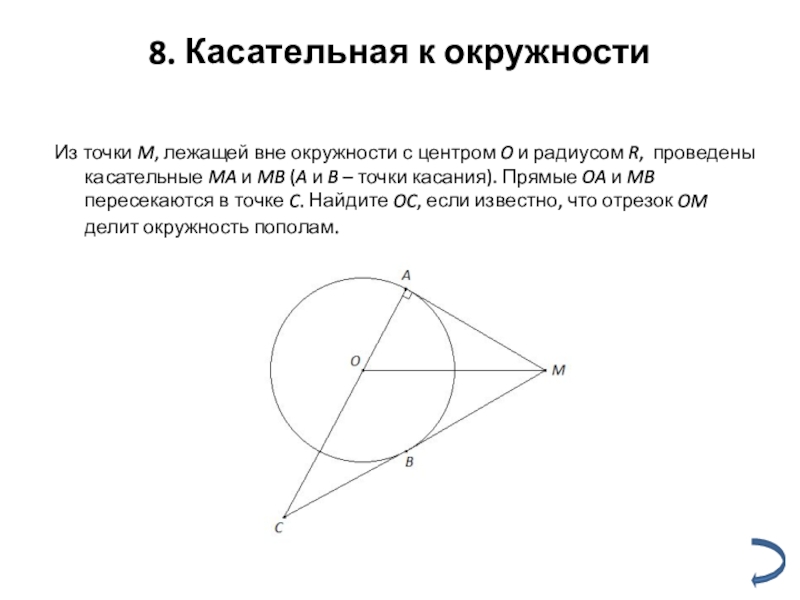
Слайд 128. Касательная к окружности
Из точки M, лежащей вне окружности с центром
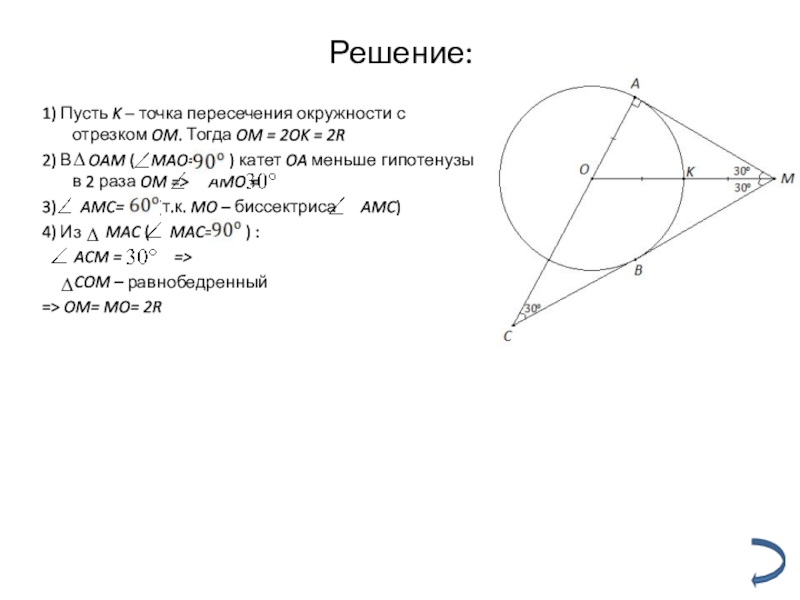
Слайд 13Решение:
1) Пусть K – точка пересечения окружности с отрезком OM. Тогда
2) В OAM ( MAO= ) катет OA меньше гипотенузы в 2 раза OM => AMO =
3) AMC= (т.к. MO – биссектриса AMC)
4) Из MAC ( MAC= ) :
ACM = =>
COM – равнобедренный
=> OM= MO= 2R
∆
∆
∆
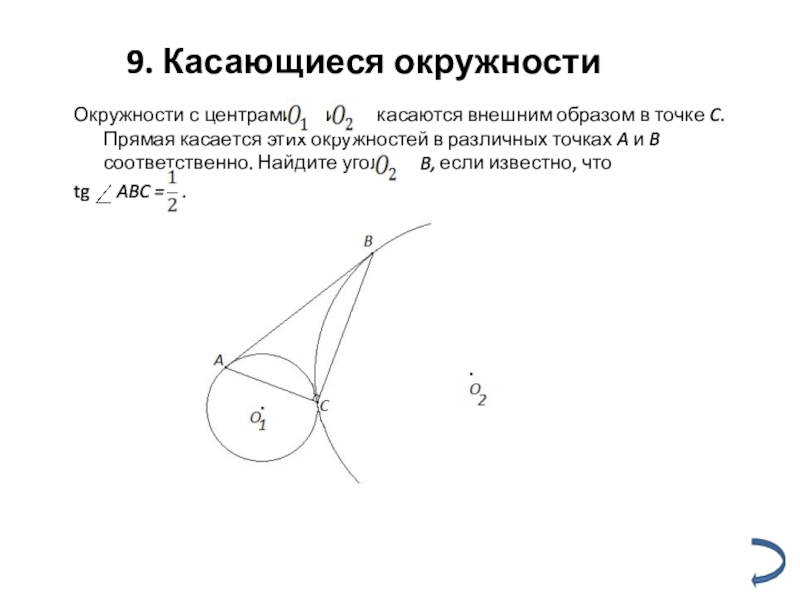
Слайд 14 9. Касающиеся окружности
Окружности с центрами и
tg ABC = .
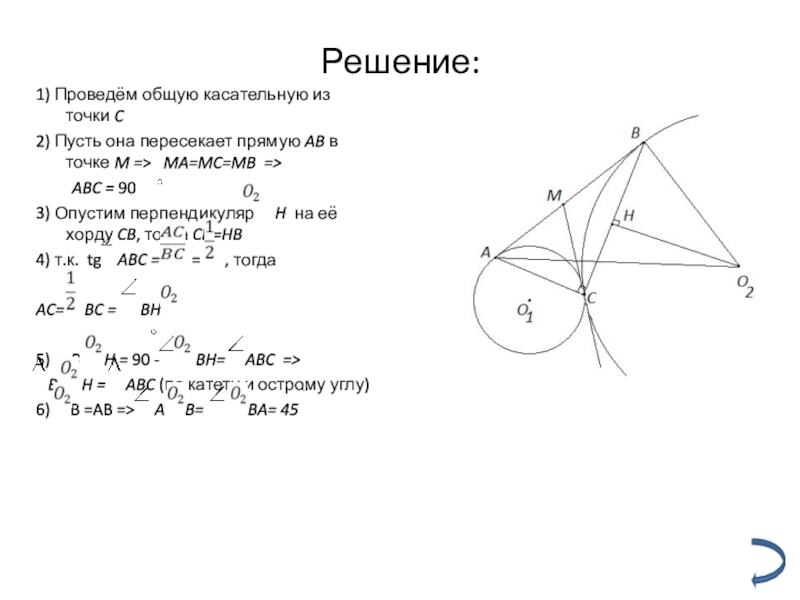
Слайд 15Решение:
1) Проведём общую касательную из точки C
2) Пусть она пересекает
ABC = 90
3) Опустим перпендикуляр H на её хорду CB, тогда CH=HB
4) т.к. tg ABC = = , тогда
AC= BC = BH
5) B H = 90 - BH= ABC =>
B H = ABC (по катету и острому углу)
6) B =AB => A B= BA= 45
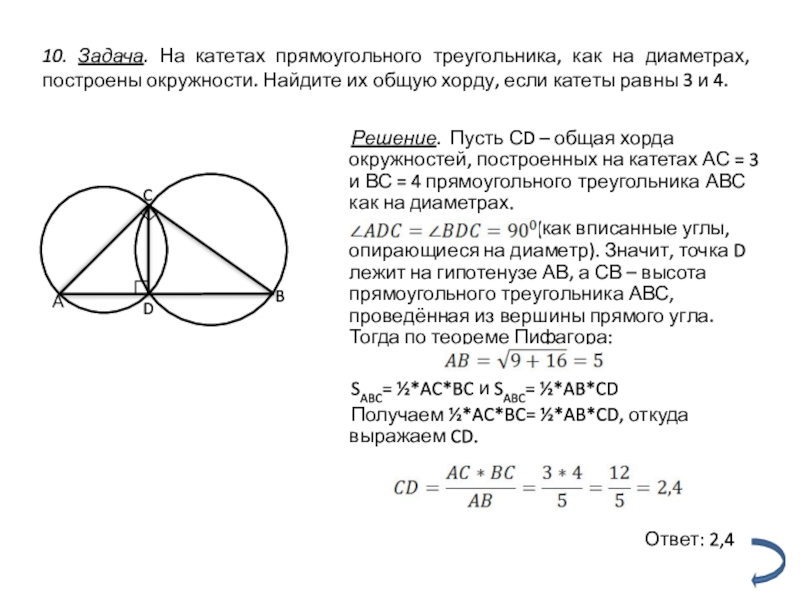
Слайд 1610. Задача. На катетах прямоугольного треугольника, как на диаметрах, построены окружности.
Решение. Пусть СD – общая хорда окружностей, построенных на катетах АС = 3 и ВС = 4 прямоугольного треугольника АВС как на диаметрах.
(как вписанные углы, опирающиеся на диаметр). Значит, точка D лежит на гипотенузе АВ, а СВ – высота прямоугольного треугольника АВС, проведённая из вершины прямого угла. Тогда по теореме Пифагора:
SABC= ½*AC*BC и SABC= ½*AB*CD
Получаем ½*AC*BC= ½*AB*CD, откуда выражаем CD.
Ответ: 2,4
А
B
C
D
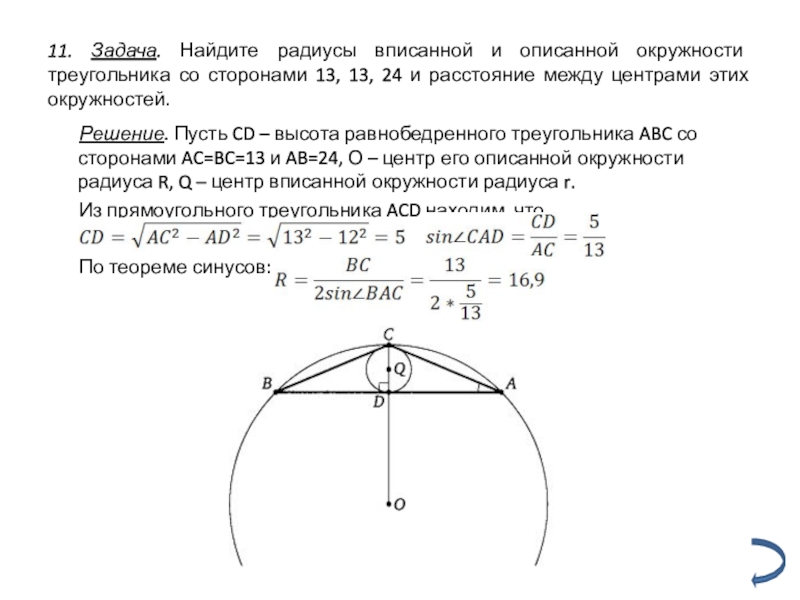
Слайд 1711. Задача. Найдите радиусы вписанной и описанной окружности треугольника со сторонами
Решение. Пусть CD – высота равнобедренного треугольника ABC со сторонами AC=BC=13 и AB=24, О – центр его описанной окружности радиуса R, Q – центр вписанной окружности радиуса r.
Из прямоугольного треугольника ACD находим, что
По теореме синусов:
Слайд 18 Радиус окружности, вписанной в треугольник, равен площади треугольника,
Заметим, что
поэтому точки O и Q лежат по разные стороны от AB. Следовательно
OQ=OC – CQ=OC – (CD – QD)= R – (CD – r)=16,9 – (5 – 2,4)=14,3
Ответ:16,9; 2,4; 14,3.
Слайд 19Пропорциональные отрезки в окружности
Теорема. Произведения отрезков пересекающихся хорд
Пример 1. Из точки А, лежащей вне окружности, проведены к окружности касательная и секущая. Расстояние от точки А до точки касания равно 16, а до одной из точек пересечения секущей с окружностью равно 32. Найдите радиус окружности, если расстояние от неё до центра секущей равно 5.
Решение. Пусть секущая пересекает окружность в точках B и C, а М – точка касания. Тогда АМ=16, АС=32, АВ+ВС=32. По теореме о касательной и секущей AM=AC*AB, или 16²=32(32-ВС). Отсюда находим, что ВС=24.
Пусть К – проекция центра О данной
окружности на хорду ВС. Радиус окружности
находим по теореме Пифагора из
прямоугольного треугольника ОКВ:
Ответ: 13
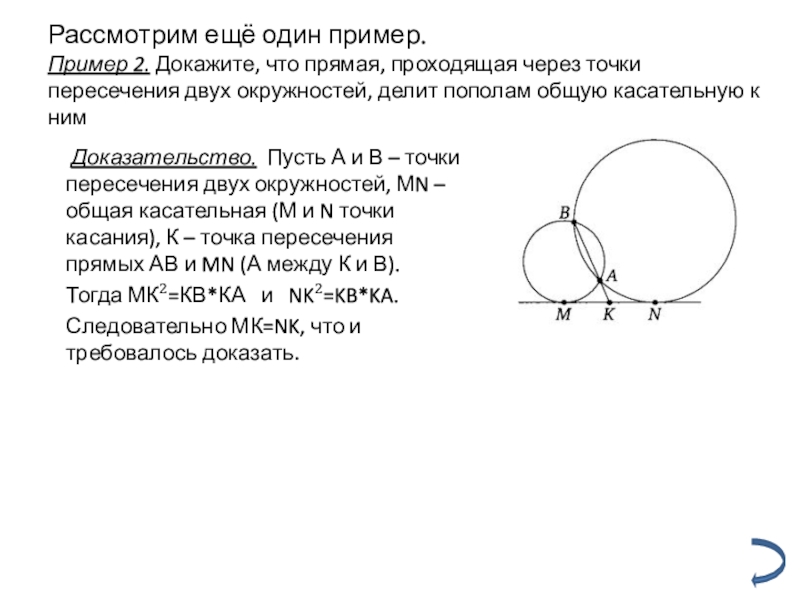
Слайд 20Рассмотрим ещё один пример. Пример 2. Докажите, что прямая, проходящая через точки
Доказательство. Пусть А и В – точки пересечения двух окружностей, МN – общая касательная (М и N точки касания), К – точка пересечения прямых АВ и MN (А между К и В).
Тогда МК²=КВ*КА и NK²=KB*KA.
Следовательно МК=NK, что и требовалось доказать.
Слайд 2112. Задача. На продолжении диаметра АВ окружности отложен отрезок ВС, равный
Решение. Пусть О – центр окружности. Тогда ОМ⏊СМ. В прямоугольном треугольнике ОМС известно, что ОМ=R и ОС=ОВ+ВС=R+2R=3R. Тогда
Следовательно,
Ответ:
Слайд 2213. Задача. Окружность S1 проходит через центр окружности S2 и пересекает
Решение. Пусть О1 и О2 – центры окружностей S1 и S2 соответственно. Тогда
Поскольку ∠О₁AC=90ᵒ (радиус, проведённый в точку касания, перпендикулярен касательной), отрезок О₂С – диаметр окружности S₁, поэтому
Тогда градусная мера дуги окружности S₂, заключённой между сторонами угла AO₂C, равна 75ᵒ, а градусная мера дуги AB окружности S₂, содержащейся внутри окружности S₁, равна 150ᵒ. Следовательно, дополнительная к ней дуга окружности S₂ равна 360ᵒ-150ᵒ=210ᵒ
Ответ: 150ᵒ, 210ᵒ
Слайд 2314. Задача. На стороне АВ треугольника АВС отмечена точка D, причём
Решение. Треугольники CBD и АВС подобны по двум углам, т.к. ∠BCD=∠BAC по условию, а угол при вершине В – общий. Значит, соответствующее стороны этих треугольников пропорциональны, т.е.
Следовательно,
Ответ:
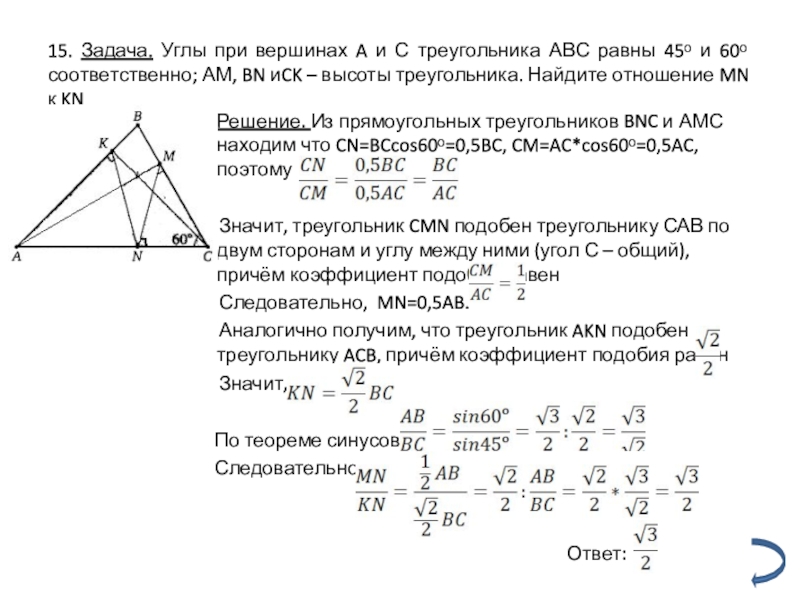
Слайд 2415. Задача. Углы при вершинах A и С треугольника АВС равны
Решение. Из прямоугольных треугольников BNC и АМС находим что CN=BCcos60ᵒ=0,5BC, CM=AC*cos60ᵒ=0,5AC, поэтому
Значит, треугольник CMN подобен треугольнику САВ по двум сторонам и углу между ними (угол С – общий), причём коэффициент подобия равен
Следовательно, MN=0,5AB.
Аналогично получим, что треугольник AKN подобен треугольнику ACB, причём коэффициент подобия равен
Значит,
По теореме синусов:
Следовательно:
Ответ: