- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Второй и третий признаки равенства треугольников
Содержание
- 1. Презентация Второй и третий признаки равенства треугольников
- 2. НО СВОЕОБРАЗНУЮ УСТОЙЧИВОСТЬ, СТАБИЛЬНОСТЬ И СОВЕРШЕНСТВО ЧИСЛА
- 3. ПОВТОРЕНИЕ:Два треугольника называются равными, если совмещаются наложениемПервый
- 4. ВТОРОЙ ПРИЗНАК РАВЕНСТВА ТРЕУГОЛЬНИКА ТЕОРЕМА:
- 5. ДАНО: △ABC, △A1B1C1
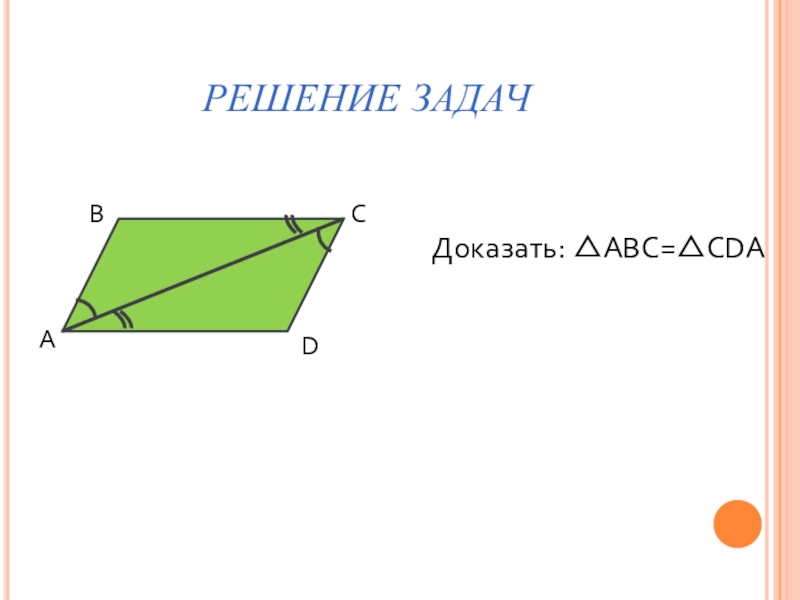
- 6. РЕШЕНИЕ ЗАДАЧАВСD Доказать: △AВС=△СDA
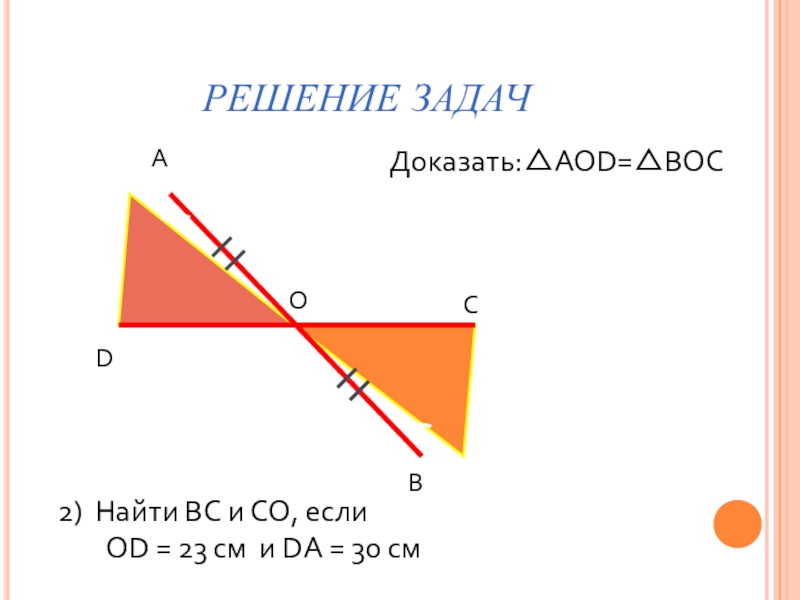
- 7. РЕШЕНИЕ ЗАДАЧАВСDОДоказать:△AOD=△BОC2) Найти ВС и СО, если
- 8. Решение задач.АCDBДАНО:∠АСВ=∠ACD,АС-биссектриса ∠ВAD.Доказать: ∆АВС=∆АDСДоказательство:1.АС-общая2. ∠АСВ=∠ACD} по усл.3. ∠1=∠2} по свойствубиссектрисы12Следовательно, ∆АВС=∆АDС ч.т.д.
- 9. 1243АСВОDДано:∠1=∠2; ∠3=∠4.Доказать: ∆АВС=∆DCB; ∆АВО=∆DCO.Доказательство:1.ВС-общая2.∠В=∠С, т.к.∠1+∠3 =∠В;
- 10. ТРЕТИЙ ПРИЗНАК РАВЕНСТВА ТРЕУГОЛЬНИКОВЕсли три стороны одного
- 11. ВАСС₁А₁В₁Дано: ∆АВС, ∆А₁В₁С₁,АВ=₁А₁В₁, ВС=В₁С₁, АС=А₁С₁.Доказать: ∆АВС=∆А₁В₁С₁Доказательство: Приложим
- 12. Возможны три случая:А₁(А)СВ₁(В)С₁∆СА₁С₁ и ∆СВ₁С₁- равнобедренные, =>∠1=∠2;∠3=∠4;
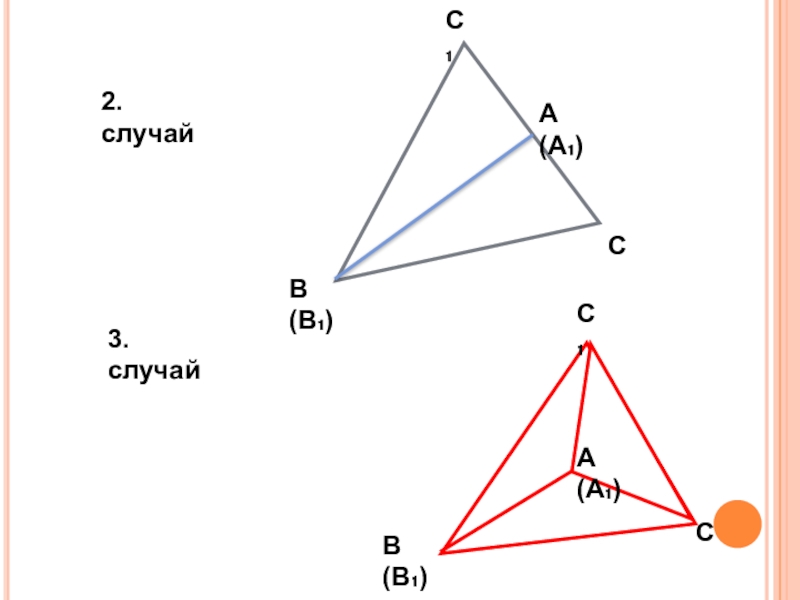
- 13. 2.случайА(А₁)В(В₁)С₁С3.случайА(А₁)С₁СВ(В₁)
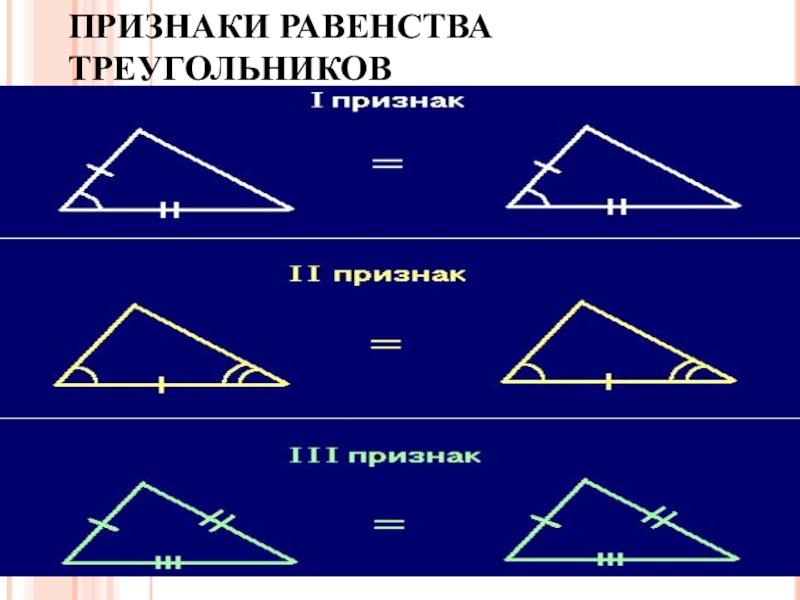
- 14. ПРИЗНАКИ РАВЕНСТВА ТРЕУГОЛЬНИКОВ
- 15. Решение задач.KMLNДано: РKLN=21 cм, РKLMN=26 см.Найти: NL.Решение:1.
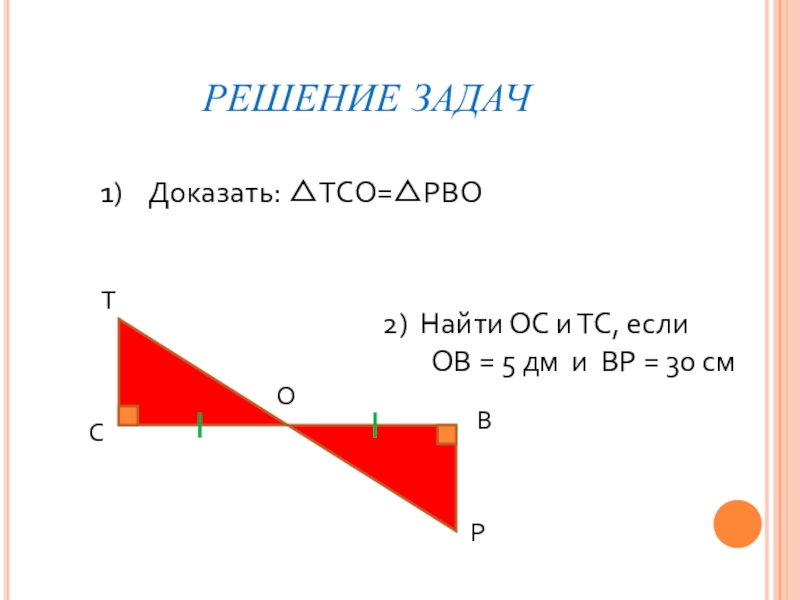
- 16. РЕШЕНИЕ ЗАДАЧТСВРОДоказать: △ТСО=△РВО2) Найти ОС и ТС,
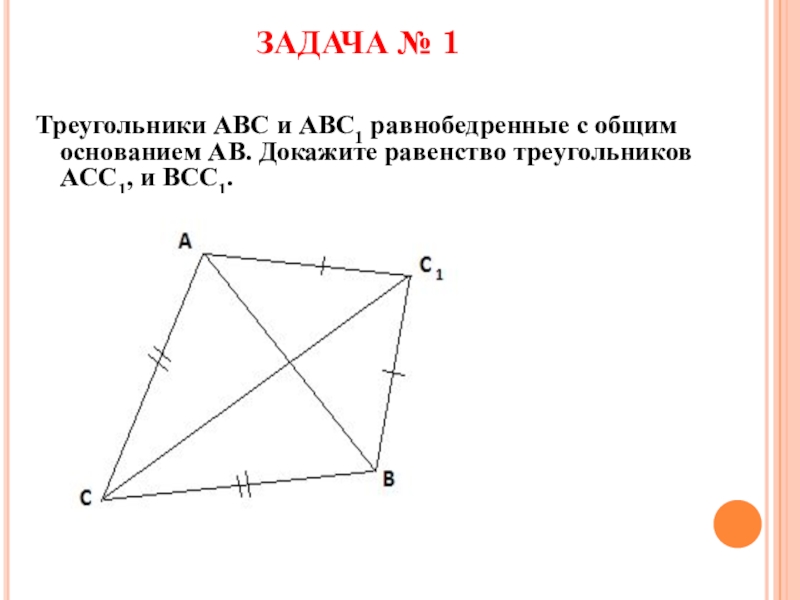
- 17. ЗАДАЧА № 1Треугольники ABC и ABC1 равнобедренные
- 18. Распределите все чертежи на группы:Равные треугольники по
- 19. Слайд 19
- 20. ДОМАШНЕЕ ЗАДАНИЕ Выучить признаки равенства треугольников, № 140, 125, 126
Слайд 2НО СВОЕОБРАЗНУЮ УСТОЙЧИВОСТЬ, СТАБИЛЬНОСТЬ И СОВЕРШЕНСТВО ЧИСЛА 3 ЛЮДИ ОЦЕНИВАЛИ И
Об этом говорят сказки.
Там мы встречаем «Три медведя», «Три ветра», «Три поросенка», «Три товарища», «Три брата», «Три счастливца», «Трое умельцев», «Три царевича», «Три друга», «Три богатыря» и др.
Там даются «три попытки», «три совета», «три указания», «три встречи», исполняются «три желания», нужно потерпеть «три дня», «три ночи», «три года», пройти через «три государства», «три подземных царства», выдержать «три испытания», проплыть через «три моря».
Слайд 3ПОВТОРЕНИЕ:
Два треугольника называются равными, если совмещаются наложением
Первый признак равенства (по двум
Если две стороны и угол между ними одного треугольника соответственно равны сторонам и углу между ними другого треугольника, то такие треугольники равны
Слайд 4ВТОРОЙ ПРИЗНАК РАВЕНСТВА ТРЕУГОЛЬНИКА ТЕОРЕМА: ЕСЛИ СТОРОНА И ДВА ПРИЛЕГАЮЩИХ К НЕЙ УГЛА
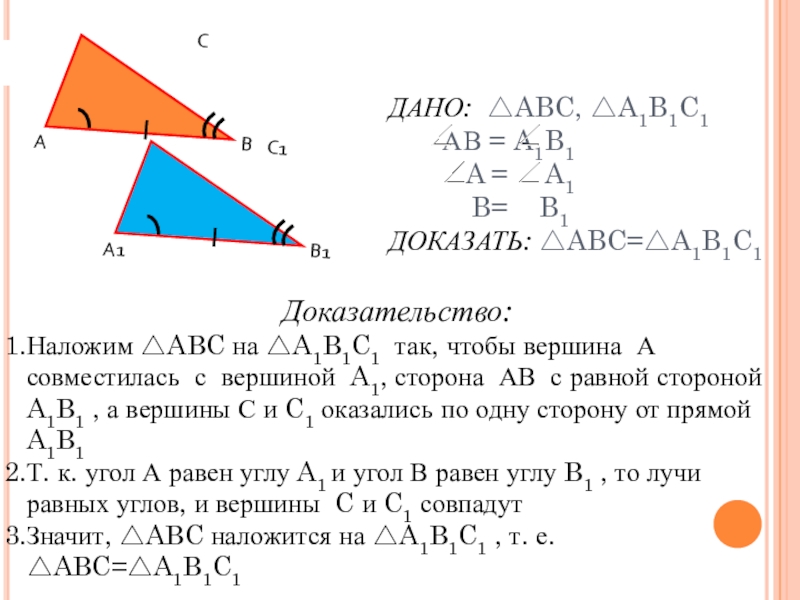
Слайд 5ДАНО: △ABC, △A1B1C1 АВ = A1B1
Доказательство:
Наложим △ABC на △A1B1C1 так, чтобы вершина А совместилась с вершиной A1, сторона АВ с равной стороной A1B1 , а вершины С и C1 оказались по одну сторону от прямой A1B1
Т. к. угол А равен углу A1 и угол В равен углу B1 , то лучи равных углов, и вершины C и C1 совпадут
Значит, △ABC наложится на △A1B1C1 , т. е. △ABC=△A1B1C1
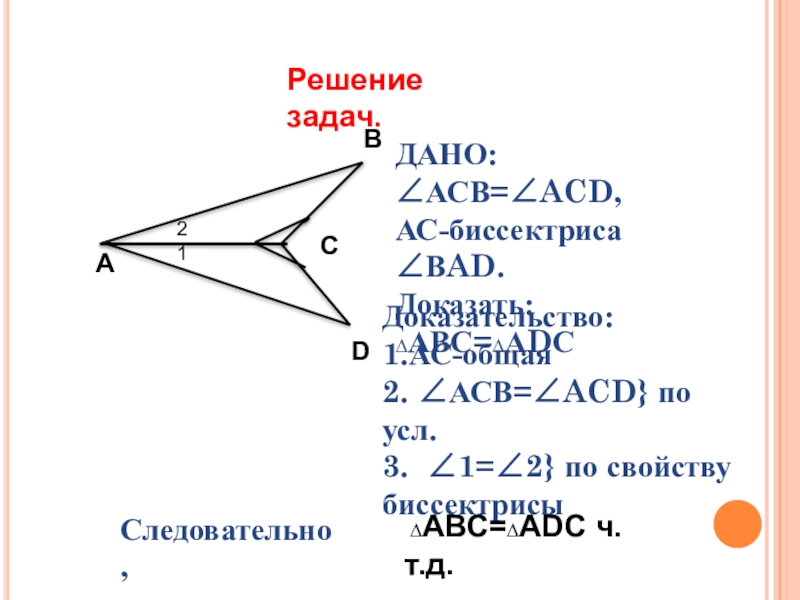
Слайд 8Решение задач.
А
C
D
B
ДАНО:∠АСВ=∠ACD,
АС-биссектриса ∠ВAD.
Доказать: ∆АВС=∆АDС
Доказательство:
1.АС-общая
2. ∠АСВ=∠ACD} по усл.
3. ∠1=∠2} по свойству
биссектрисы
1
2
Следовательно,
∆АВС=∆АDС
Слайд 91
2
4
3
А
С
В
О
D
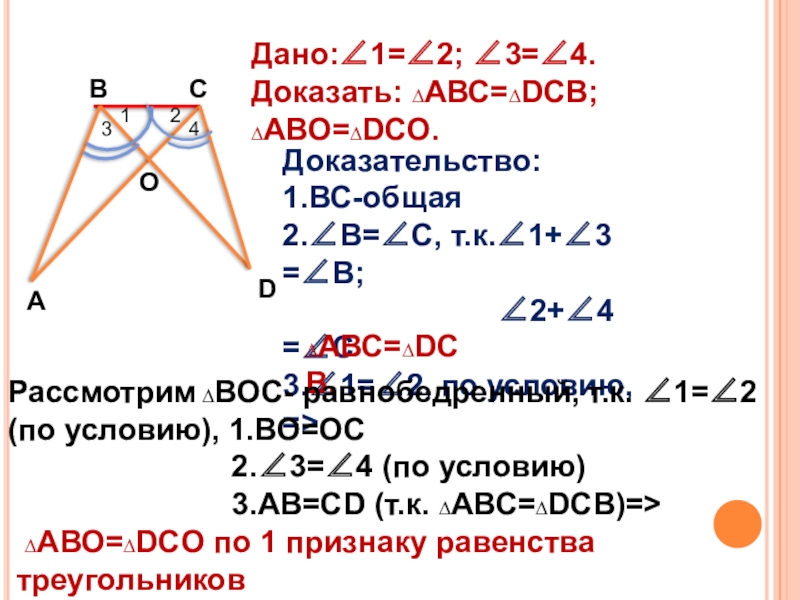
Дано:∠1=∠2; ∠3=∠4.
Доказать: ∆АВС=∆DCB; ∆АВО=∆DCO.
Доказательство:
1.ВС-общая
2.∠В=∠С, т.к.∠1+∠3 =∠В;
3.∠1=∠2, по условию, =>
∆АВС=∆DCB.
Рассмотрим ∆ВОС- равнобедренный, т.к. ∠1=∠2
(по условию), 1.ВО=ОС
2.∠3=∠4 (по условию)
3.АВ=СD (т.к. ∆АВС=∆DСВ)=>
∆АВО=∆DCO по 1 признаку равенства
треугольников
Слайд 10ТРЕТИЙ ПРИЗНАК РАВЕНСТВА ТРЕУГОЛЬНИКОВ
Если три стороны одного треугольника соответственно равны трем
Слайд 11
В
А
С
С₁
А₁
В₁
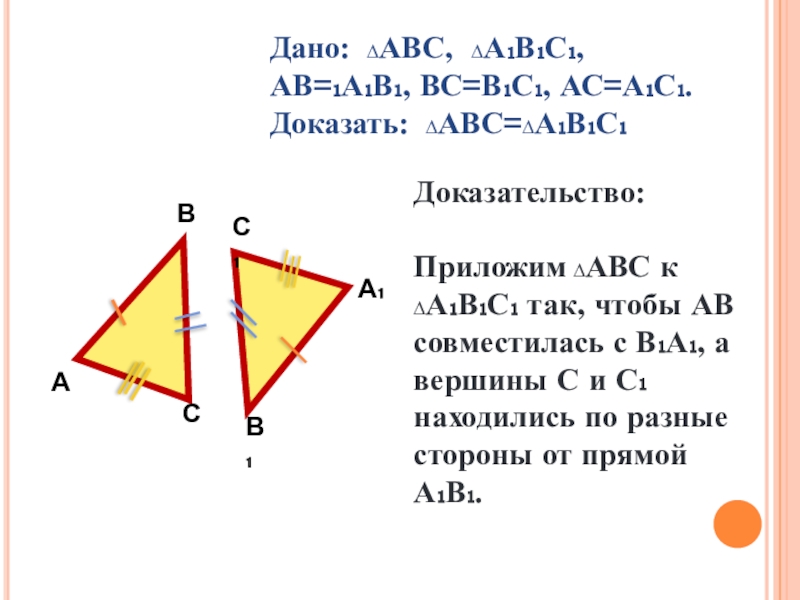
Дано: ∆АВС, ∆А₁В₁С₁,
АВ=₁А₁В₁, ВС=В₁С₁, АС=А₁С₁.
Доказать: ∆АВС=∆А₁В₁С₁
Доказательство:
Приложим ∆АВС к ∆А₁В₁С₁ так,
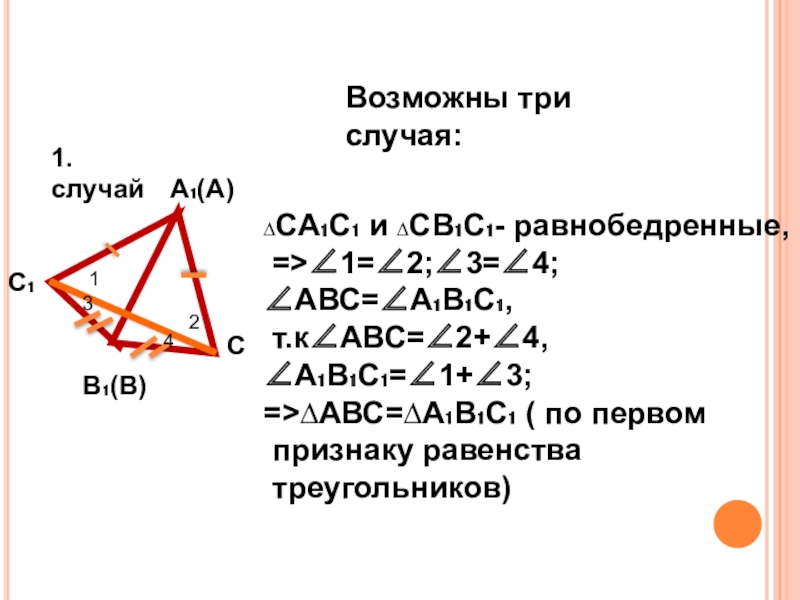
Слайд 12Возможны три случая:
А₁(А)
С
В₁(В)
С₁
∆СА₁С₁ и ∆СВ₁С₁- равнобедренные,
=>∠1=∠2;∠3=∠4; ∠АВС=∠А₁В₁С₁,
т.к∠АВС=∠2+∠4, ∠А₁В₁С₁=∠1+∠3;
=>∆АВС=∆А₁В₁С₁ (
признаку равенства
треугольников)
2
1
4
3
1. случай
Слайд 15Решение задач.
K
M
L
N
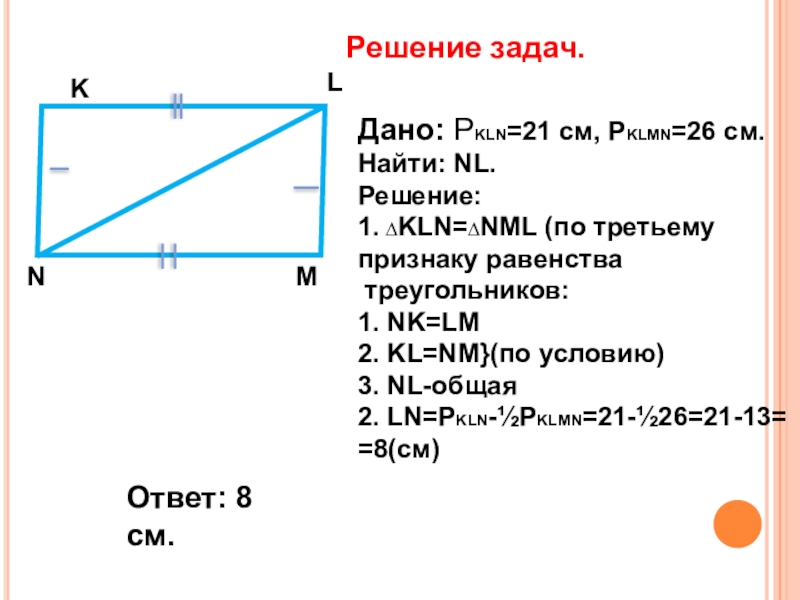
Дано: РKLN=21 cм, РKLMN=26 см.
Найти: NL.
Решение:
1. ∆KLN=∆NML (по третьему
признаку равенства
1. NK=LM
2. KL=NM}(по условию)
3. NL-общая
2. LN=PKLN-½PKLMN=21-½26=21-13=
=8(cм)
Ответ: 8 см.
Слайд 17ЗАДАЧА № 1
Треугольники ABC и ABC1 равнобедренные с общим основанием AB.
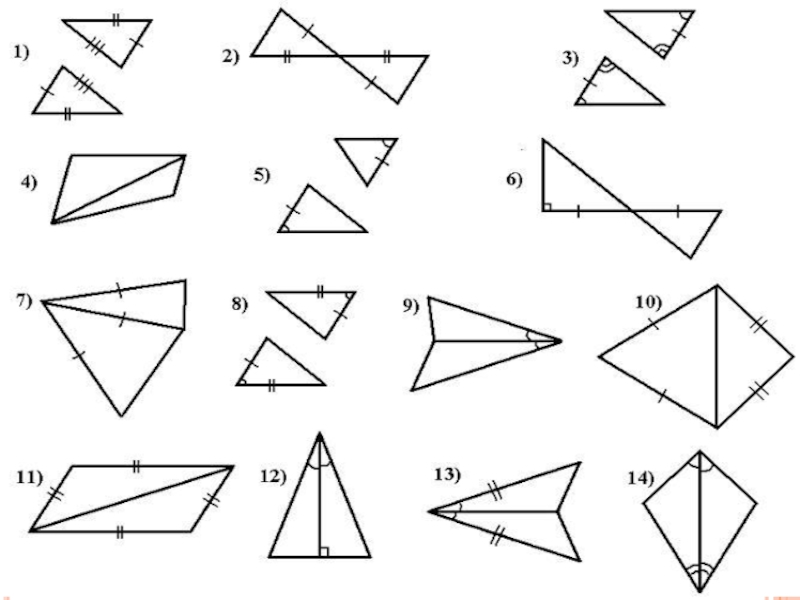
Слайд 18Распределите все чертежи на группы:
Равные треугольники по первому признаку
Равные треугольники по
Равные треугольники по третьему признаку
Треугольники не равны или невозможно определить
ЗАДАНИЕ