- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад урока Теорема Пифагора
Содержание
- 1. Презентация урока Теорема Пифагора
- 2. Цель урока: отработать применение практических навыков при
- 3. «Пребудет вечной истина, как скоро
- 4. Пифагор Самосский (ок. 580 — ок. 500
- 5. Рафаэль Санти. Пифагор (деталь Афинской школы). Школа
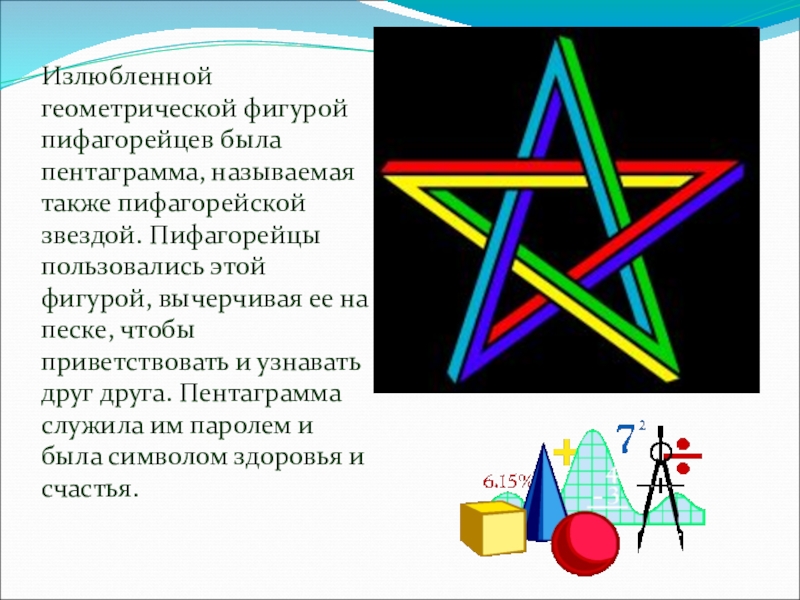
- 6. Излюбленной геометрической фигурой пифагорейцев была пентаграмма, называемая
- 7. Предание гласит, что когда Пифагор пришёл к
- 8. Актуализация знаний учащихся1.Теоретический опрос. Прямоугольный треугольник.Сформулировать теорему Пифагора.Индивидуальное письменное задание доказать теорему Пифагора.2. Математический диктант.
- 9. Прямоугольный треугольникУгол С = 90°ACBкатеткатетгипотенузаКакой треугольник называется
- 10. Теорема Пифагора:В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.ABCbсаa²+b²=c²
- 11. Математический диктант Выбери правильный вариант ответа.1. Закончи предложение: “Треугольник,
- 12. Решение задач на готовых чертежах вариант 1
- 13. Решение:Вариант 1.1)AB²=AC²+CB²AB²=20²+15²AB²=625AB=252)ACD-прямоуг.AC²=AD²+DC²AC²=4²+3²AC²=25AC=53)ABD прямоуг.AD²=AB²-BD²AD²=13²-12²AD²=25AD=5AC=2AD=2*5=10Вариант 21)AB²=AC²+CB²BC²=AB²-AC²BC²=10²-6²BC²=64BC=82) BAD- прямоуг.BA²=BD²-AD²BA²=10²-8²BA²=36BA=63)AD=½AC=10ABD прямоуг.AB²=AD²+BD²AB²=10²+24²AB²=676AB=26
- 14. Самостоятельная работа
- 15. Самостоятельная работа
- 16. III Взаимопроверка работ в парах (готовое решение
- 17. IV. Рефлексия (подведение итогов урока) Чему вы
- 18. V. Домашнее задание. 1 базовый .№489а); №491а); №493 2 повышенный: №495 в);№522.
- 19. Спасибо за урок!
Слайд 1Теорема Пифагора
Урок геометрии в 8 классе
Разработала
Учитель математики МБОУ « Левженская СОШ» Рузаева Елена Борисовна
Слайд 2Цель урока: отработать применение практических навыков при решении группы задач по
Задачи урока:
Образовательные: . Научиться решать задачи по теме «Теорема Пифагора», используя алгоритм решения «ключевых» задач.
Развивающие: Развивать логическое мышление учащихся, пространственные представления ,познавательную активность учащихся.
Воспитательные: содействовать воспитанию интереса к математике, активности, организованности, умения общаться.
Тип урока - - повторительно-обобщающий
Форма урока -практикум
Оборудование: экран, компьютер, проектор, карточки с дифференцированным заданием.
Слайд 3
«Пребудет вечной истина, как скоро
Ее познает слабый человек!
Верна, как и в его далекий век.»
сонет Шамиссо
Слайд 4Пифагор Самосский (ок. 580 — ок. 500 до н. э.) —
Слайд 5Рафаэль Санти. Пифагор (деталь Афинской школы).
Школа Пифагора, или, как ее
Слайд 6Излюбленной геометрической фигурой пифагорейцев была пентаграмма, называемая также пифагорейской звездой. Пифагорейцы
Слайд 7Предание гласит, что когда Пифагор пришёл к теореме, носящей его имя,
В настоящее время известно около 200 доказательств теоремы Пифагора.
Слайд 8Актуализация знаний учащихся
1.Теоретический опрос.
Прямоугольный треугольник.
Сформулировать теорему Пифагора.
Индивидуальное письменное задание
2. Математический диктант.
Слайд 9Прямоугольный треугольник
Угол С = 90°
A
C
B
катет
катет
гипотенуза
Какой треугольник называется прямоугольным?
Как называются стороны,
Образующие прямой
Как называется сторона,
лежащая напротив прямого
угла?
Слайд 10Теорема Пифагора:
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
A
B
C
b
с
а
a²+b²=c²
Слайд 11Математический диктант
Выбери правильный вариант ответа.
1. Закончи предложение: “Треугольник, у которого один угол
а) остроугольный; б) равнобедренный; в) равносторонний; г) прямоугольный;
2. Как называются стороны в прямоугольном треугольнике?
а) боковые стороны; б) основания; в) катеты и гипотенуза.
4. У какого треугольника правильно отмечены стороны.
5. Закончи предложение “Косинусом острого угла называется отношение…..”
а) противолежащего катета к гипотенузе; б) прилежащего катета к гипотенузе; в) прилежащего катета к противолежащему катету; г) противолежащего катета к прилежащему катету.
6.Выбрать формулу площади квадрата.
Слайд 12Решение задач на готовых чертежах вариант 1
1 )треугольник АВС -прямоугольный. Найти АВ
2)ABCD-прямоугольник. Найти АС.
3)тр.АВС-равнобедренный,BD-высота,АС-основание.Найти АС,если BD =12, BA =13
.
1)треугольник АВС –
прямоугольный. Найти СВ.
2)ABCD-прямоугольник. Найти BA .
3) тр.АВС-равнобедренный, BD-высота, АС- основание. Найти АВ, если АС=20, BD=24.
C
A
B
A
D
B
C
A
B
C
D
C
A
B
A
B
C
D
A
B
C
D
20
15
4
3
6
10
10
8
Слайд 13Решение:
Вариант 1.
1)AB²=AC²+CB²
AB²=20²+15²
AB²=625
AB=25
2)ACD-прямоуг.
AC²=AD²+DC²
AC²=4²+3²
AC²=25
AC=5
3)ABD прямоуг.
AD²=AB²-BD²
AD²=13²-12²
AD²=25
AD=5
AC=2AD=2*5=10
Вариант 2
1)AB²=AC²+CB²
BC²=AB²-AC²
BC²=10²-6²
BC²=64
BC=8
2) BAD- прямоуг.
BA²=BD²-AD²
BA²=10²-8²
BA²=36
BA=6
3)AD=½AC=10
ABD прямоуг.
AB²=AD²+BD²
AB²=10²+24²
AB²=676
AB=26
Слайд 14Самостоятельная работа
1.Уровень
Вариант 1
1. Диагонали ромба 12 см и 16 см Найти сторону ромба
2. В треугольнике АВС, С = 900, В = 300, СВ = 5 см, АВ = 12 см. Найти площадь треугольника.
Вариант 2
1. Стороны прямоугольника 5 см и 12 см. Найти диагональ прямоугольника.
2. В ABC С = 900, А = 450, АВ = 8 см, АС = 3 см. Найти площадь треугольника.
Слайд 15Самостоятельная работа
2.Уровень
1. В
2. Высота параллелограмма равны 4 см и 5см, а периметр равен 42 см. Найти площадь параллелограмма
В прямоугольной трапеции боковые стороны равны 15 см и 9 см, а большее основание 20 см. Найти площадь трапеции.
2. Диагонали ромба равны 18 и 24 см. Найти периметр ромба и расстояние между параллельными сторонами.
Слайд 16III Взаимопроверка работ в парах (готовое решение на доске).
Решение задач
Вариант - 1
Дано: ABCD – ромб
АС = 12 см
BD = 16 см , (Рисунок5)
Найти: АВ
Решение:
Рассмотрим ∆ АОВ, О = 900; АО = 6 см, ВО = 8 см (свойства диагоналей ромба)
По теореме Пифагора: АВ2 = АО2 + ВО2
АВ2 = 36 + 64 = 100
АВ = 10 см
Ответ: 10 см
Дано: ∆АВС, С = 900, В = 300
СВ = 5 см, АВ = 12 см, (Рисунок6)
Найти: S∆АВС
Решение:
S∆ = , АС = = 6 см (катет лежит против угла 300)
S∆ = = 15 см2
Ответ: 15 см2
Вариант - 2
Дано: АВСD прямоугольник
АВ = 5 см
АD = 12 см, (рисунок7)
Найти: BD
Решение:
∆АВD – прямоугольный
По теореме Пифагора:
ВD2 = АB2 + AD2
BD2 = 25 + 144 = 169
BD = 13 см
Ответ: 13 см
Дано: ∆АВС, С = 900, А = 450
АС = 3 см, АВ = 8 см, (Рисунок 8)
Найти: S∆АВС
Решение:
S∆ = ,
А = В = 450 (свойства острых углов прямоугольного треугольника), значит
АС = СВ = 3 см
S∆ = = 4,5 см2
Решение задач 2 – уровня
Вариант - 1
Дано: ABCD – трапеция
AD = 17 см
ВС = 5 см
АВ = 13 см
С = 900, (Рисунок9)
Найти: Sтрапеции
Решение:
BH AD, HD = BC = 5 см (BCDH – прямоугольник)
АН = 17 – 5 = 12 см
По теореме Пифагора получаем
AB2 = АH2 + BH2
BH2 = AB2 - АH2 = 169 – 144 = 25
BH = 5 см
Sтрап =
Sтрап = 55 см2
Ответ: 55 см2
Дано: ABCD – параллелограмм
BH, BN – высоты, BH = 4 см, BN = 5см
PABCD = 42 см, (Рисунок10)
Найти: SABCD
Решение:
Пусть АВ = х см, АD = y см,
x + y = 21
x = 21 – y;
SABCD = AD * BH = CD * BN
y * 4 = (21 - y) * 5
4 y = 105 – 5 y
9 y = 105; y = 11
Значит AD = 11 см
SABCD = AD * BH
SABCD = 11 * 4 = 46 см2
Ответ: 46 см2
Вариант – 2
Дано: Дано: ABCD – трапеция
AD = 20 см
СD = 5 см
АВ = 9 см
А = 900,(Рисунок11)
Найти: SABCD
Решение:
CO AD, CO = BA = 9 см
COD : О = 900 по теореме Пифагора:
CD2 = CO2 + OD2
OD2 = CD2 – OC2 = 125 – 81 = 144
OD = 12 см, Значит АО = ВС = 20 – 12 = 8 см
SABCD =
SABCD = 126 см2
Дано: ABCD – ромб
АС =18 см
BD = 24 см, (Рисунок12)
Найти:
P ромба
Расстояние между АВ и СD
Решение:
АВО, О = 900 (свойства диагоналей ромба)
АО = 9 см, ОВ = 12 см по теореме Пифагора:
АВ2 = АО2 + ВО2
АВ2 = 81 + 144 = 225
АВ = 15 см
PABCD = 4 * 15 = 60 см
АН DC, AH – расстояние между АВ и DC
SABCD = и
SABCD = АН * CD,
AH = =
AH = = 14,4 cм
Слайд 17IV. Рефлексия (подведение итогов урока)
Чему вы научились при изучении темы раздела;
Какими
Какими формулами, понятиями воспользовались при решении задач?
Решение каких задач показалось вам сложным?
Какие вопросы требуется вашего особого внимания?
Какие задачи вам понравилось решать?