- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад урока по геометрии в 7 классе Равнобедренный треугольник
Содержание
- 1. Презентация урока по геометрии в 7 классе Равнобедренный треугольник
- 2. Крыши домов и башен
- 3. Слайд 3
- 4. Египетские пирамиды
- 5. Слайд 5
- 6. Северные росписи
- 7. Слайд 7
- 8. а) Вопрос – ответ 1. Какой отрезок
- 9. Из следующих пяти треугольников только три
- 10. б) BD на рисунке … является …ВысотаМедиана Биссектриса
- 11. Какая фигура называется треугольником? 2) Какие
- 12. Тема: Равнобедренный треугольник.
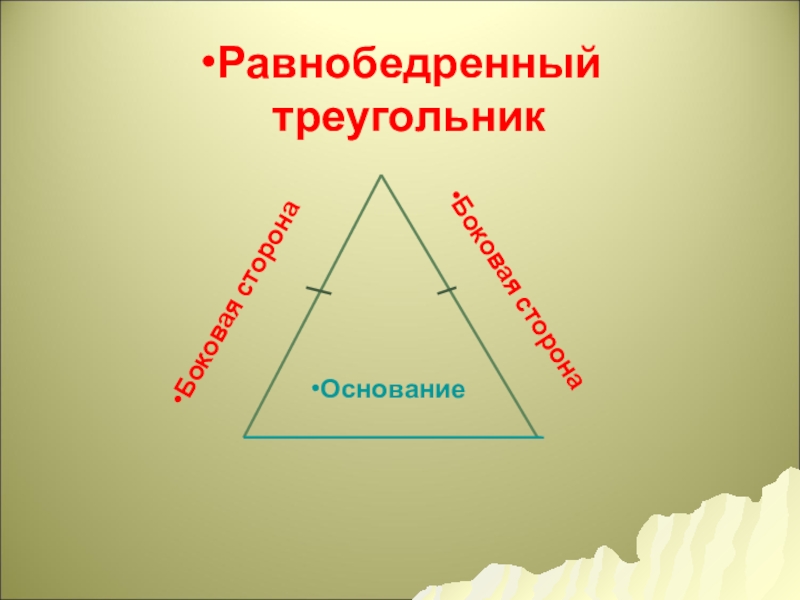
- 13. Боковая сторонаБоковая сторонаОснованиеРавнобедренный треугольник
- 14. KDMДан ∆ MKD,где MK=KD.Назовите боковые стороны.Назовите основание.Углы при основании.Угол противолежащий основанию. Задание 1.
- 15. CDELCDKMNTNP1.Какие из треугольников являются равнобедренными?2.Треугольник NTP можно отнести к равнобедренным?3.Почему?4.Тогда назовите боковые стороны, основания.665648554555Задание 2.
- 16. TNP Равносторонний треугольник является частным
- 17. Круги Эйлера.равнобедренные(мусавий кенарлы)равносторонние(мусавий янлы)разносторонние(чешит янлы)
- 18. Физкультминутка
- 19. DBCДано: ∆ АВС равнобедренный треугольникАВ=АСР∆ АВС= 40 см∆ ВСD- равносторонний треугольникР∆ ВСD= 45 см.Найти: АВ, ВСА
- 20. Проверь себя.,Решение:Р∆ АВС = AB + AC
- 21. Теорема. В равнобедренном треугольнике углы при основании
- 22. Найти неизвестные углы:
- 23. В равнобедренном треугольнике боковая сторона равна 10
- 24. Практическая работаНачертите равнобедренный треугольник АВС с основанием
- 25. ВАСDДано:∆АВС, AB = АC,АD – биссектриса
- 26. АВСК∆ АВС –равнобедренный,АС – основание, ВК –
- 27. Теоретический тест1.Медиана в равнобедренном треугольнике является его
- 28. Кроссворд1.Единица измерения углаРезультат сложенияЧетырехугольник, у которого все
- 29. Кроссворд1.Единица измерения углаРезультат сложенияЧетырехугольник, у которого все
- 30. Кроссворд1.Единица измерения углаРезультат сложенияЧетырехугольник, у которого все
- 31. Кроссворд1.Единица измерения углаРезультат сложенияЧетырехугольник, у которого все
- 32. Кроссворд1.Единица измерения углаРезультат сложенияЧетырехугольник, у которого все
- 33. Кроссворд1.Единица измерения углаРезультат сложенияЧетырехугольник, у которого все
- 34. Кроссворд1.Единица измерения углаРезультат сложенияЧетырехугольник, у которого все
- 35. Кроссворд1.Единица измерения углаРезультат сложенияЧетырехугольник, у которого все
- 36. Кроссворд1.Единица измерения углаРезультат сложенияЧетырехугольник, у которого все
- 37. Кроссворд1.Единица измерения углаРезультат сложенияЧетырехугольник, у которого все
- 38. Кроссворд1.Единица измерения углаРезультат сложенияЧетырехугольник, у которого все
- 39. Кроссворд1.Единица измерения углаРезультат сложенияЧетырехугольник, у которого все
- 40. Кроссворд1.Единица измерения углаРезультат сложенияЧетырехугольник, у которого все
- 41. Кроссворд1.Единица измерения углаРезультат сложенияЧетырехугольник, у которого все
- 42. КроссвордЕдиница измерения углаРезультат сложенияЧетырехугольник, у которого все
- 43. СПАСИБО ЗА ВНИМАНИЕ!
Слайд 1Тема урока
«Равнобедренный треугольник (Мусавий кенарлы учькошелик)»
Сейтаблаева Ф.М.,
учитель математики Старокрымской ОШ
Слайд 8
а) Вопрос – ответ
1. Какой отрезок называется перпендикуляром, проведенным из
2. Сформулируйте теорему о сумме углов треугольника.
3. Какой отрезок называется биссектрисой треугольника? Сколько биссектрис имеет треугольник?
4. Какой отрезок называется высотой треугольника? Сколько высот имеет треугольник?
5. Какой отрезок называется медианой треугольника? Сколько медиан имеет треугольник?
6. Первый признак равенства треугольников.
7. Второй признак равенства треугольников.
Слайд 9Из следующих пяти треугольников
только три равных.
Запишите их номера.
№ 1, № 3, № 4
1
2
3
4
5
Слайд 11 Какая фигура называется треугольником?
2) Какие виды треугольников Вы знаете?
3)
сюйрю кошели
токъал кошели
тюз кошели
мусавий кенарлы
мусавий янлы
Слайд 12Тема: Равнобедренный треугольник.
Равнобедренный и равносторонний треугольник.
Свойство углов равнобедренного треугольника.
Свойство медианы (биссектрисы, высоты) равнобедренного треугольника.
Слайд 14K
D
M
Дан ∆ MKD,где MK=KD.
Назовите боковые стороны.
Назовите основание.
Углы при основании.
Угол противолежащий основанию.
Задание 1.
Слайд 15C
D
E
L
C
D
K
M
N
T
N
P
1.Какие из треугольников являются равнобедренными?
2.Треугольник NTP можно отнести к равнобедренным?
3.Почему?
4.Тогда назовите
6
6
5
6
4
8
5
5
4
5
5
5
Задание 2.
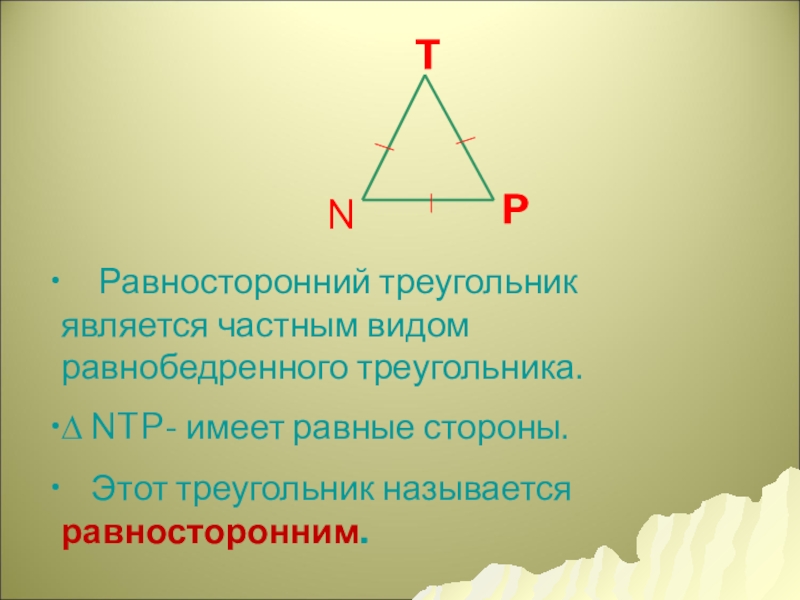
Слайд 16T
N
P
Равносторонний треугольник является частным видом равнобедренного треугольника.
∆
Этот треугольник называется равносторонним.
Слайд 17
Круги Эйлера.
равнобедренные
(мусавий кенарлы)
равносторонние
(мусавий янлы)
разносторонние
(чешит янлы)
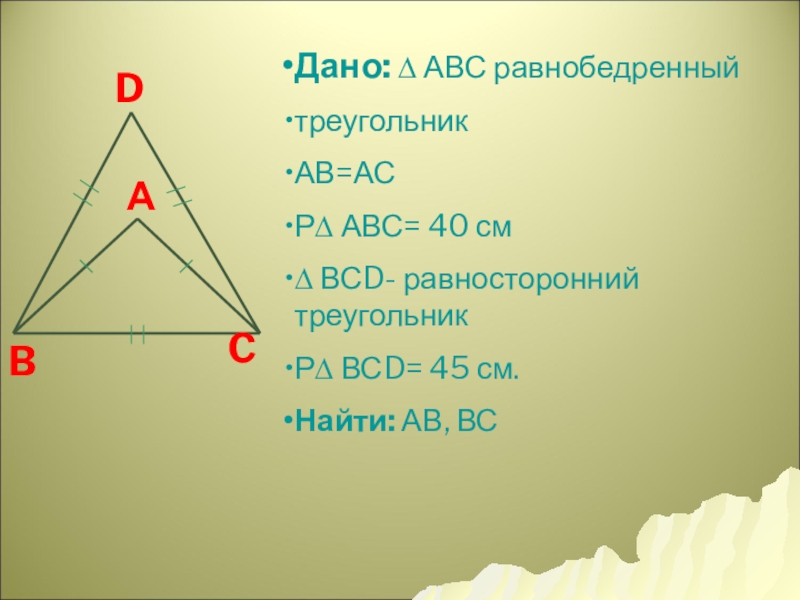
Слайд 19D
B
C
Дано: ∆ АВС равнобедренный
треугольник
АВ=АС
Р∆ АВС= 40 см
∆ ВСD- равносторонний треугольник
Р∆
Найти: АВ, ВС
А
Слайд 20Проверь себя.
,
Решение:
Р∆ АВС = AB + AC + BC=2AB+BC, по определению
∆ ВСD = BD + DC + BC = 3AB, по определению равностороннего треугольника, т. к. BD=DC=BC.
BC= ∆ ВСD/3 = 45/3=15 см.
Р∆ АВС =40 см, 40 = 2AB+BC=2AB +15, AB =(40-15)/2 =12,5 см.
Записываем ответ. Ответ: 15 см, 12,5 см.
.
Ответ:15см,12,5см.
Слайд 21Теорема. В равнобедренном треугольнике углы при основании равны.
Дано: ▲ АВС, АВ
Доказательство:
Пусть AD – биссектриса ▲ АВС.
Рассмотрим ▲ABD и ▲ACD.
Слайд 23
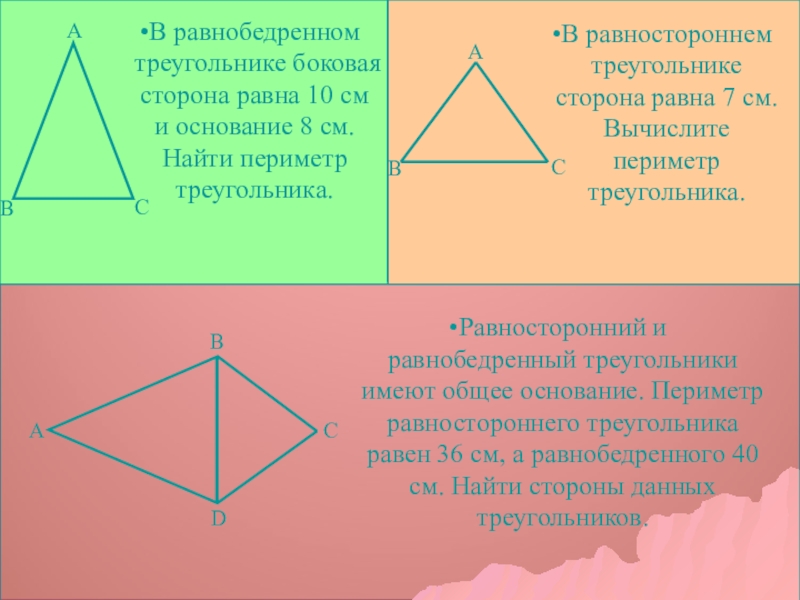
В равнобедренном треугольнике боковая сторона равна 10 см и основание 8
А
С
В
В равностороннем треугольнике сторона равна 7 см. Вычислите периметр треугольника.
А
В
С
А
В
С
D
Равносторонний и равнобедренный треугольники имеют общее основание. Периметр равностороннего треугольника равен 36 см, а равнобедренного 40 см. Найти стороны данных треугольников.
Слайд 24Практическая работа
Начертите равнобедренный треугольник АВС с основанием ВС.
С помощью транспортира и
С помощью чертежного угольника проведите высоту из вершины А.
С помощью масштабной линейки проведите медиану из вершины А.
Что вы заметили? Что вас удивило?
Попробуйте высказать гипотезу.
Слайд 25
В
А
С
D
Дано:
∆АВС, AB = АC,
АD – биссектриса
Теорема: В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.
1
2
План 1) Доказать, что ∆ АВD = ∆ АCD;
2) Выписать соответственно равные стороны и углы;
3) Сделать вывод.
Слайд 26А
В
С
К
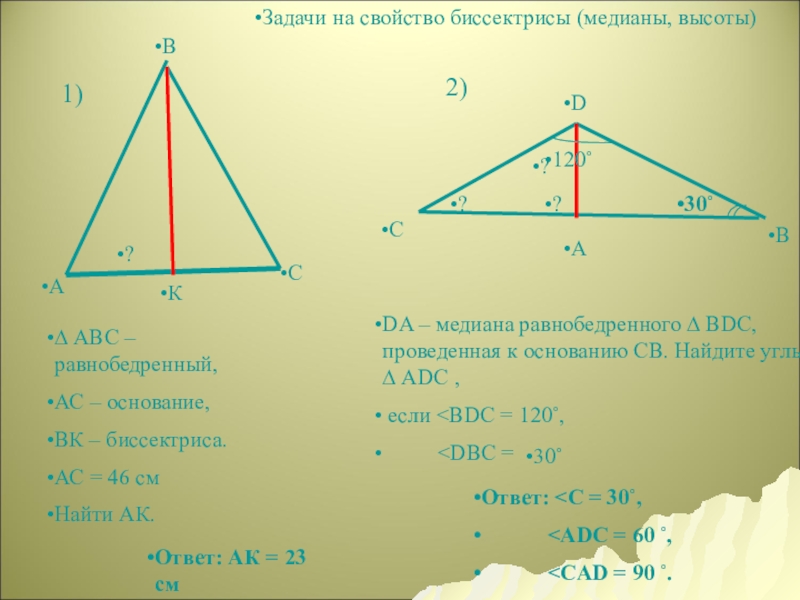
∆ АВС –равнобедренный,
АС – основание,
ВК – биссектриса.
АС = 46 см
Найти
D
А
С
В
DA – медиана равнобедренного ∆ ВDС, проведенная к основанию СВ. Найдите углы ∆ АDС , 30˚ 30˚ 120˚ ? ? ? Задачи на свойство биссектрисы (медианы, высоты) ? Ответ: АК = 23 см Ответ: 2) 1)
если
Слайд 27Теоретический тест
1.Медиана в равнобедренном треугольнике является его биссектрисой и высотой. Это
а) всегда верно;
б) может быть верно;
в) всегда неверно.
2. Если треугольник равносторонний, то:
а) он равнобедренный;
б) все его углы равны;
в) любая его высота является медианой и биссектрисой.
3. В каком треугольнике только одна его высота делит треугольник на два равных треугольника?
а) в любом;
б) в равнобедренном;
в) в равностороннем.
4. Биссектриса в равностороннем треугольнике является медианой и высотой. Это утверждение:
а) всегда верно;
б) может быть верно;
в) всегда неверно.
5. Если треугольник равнобедренный, то:
а) он равносторонний;
б) любая ее медиана является биссектрисой и высотой;
в) ответы а) и б) неверны.
6. В каком треугольнике любая его высота делит треугольник на два равных треугольника?
а) в любом;
б) в равнобедренном;
в) в равностороннем.
Слайд 28Кроссворд
1.Единица измерения угла
Результат сложения
Четырехугольник, у которого все стороны равны и все
Результат вычитания
Угол, равный 90º
Четырехугольник, у которого все стороны равны
Сотая часть какого-нибудь числа
Отрезок, соединяющий вершины треугольника с серединой противоположной стороны
Угол, градусная мера которого меньше 90º
Луч, делящий угол пополам
Углы, образованные при пересечении двух прямых
Прямые, которые лежат на одной плоскости и никогда не пересекаются
Арифметическое действие
Угол, градусная мера которого больше 90º
Слайд 29Кроссворд
1.Единица измерения угла
Результат сложения
Четырехугольник, у которого все стороны равны и все
Результат вычитания
Угол, равный 90º
Четырехугольник, у которого все стороны равны
Сотая часть какого-нибудь числа
Отрезок, соединяющий вершины треугольника с серединой противоположной стороны
Угол, градусная мера которого меньше 90º
Луч, делящий угол пополам
Углы, образованные при пересечении двух прямых
Прямые, которые лежат на одной плоскости и никогда не пересекаются
Арифметическое действие
Угол, градусная мера которого больше 90º
Слайд 30Кроссворд
1.Единица измерения угла
Результат сложения
Четырехугольник, у которого все стороны равны и все
Результат вычитания
Угол, равный 90º
Четырехугольник, у которого все стороны равны
Сотая часть какого-нибудь числа
Отрезок, соединяющий вершины треугольника с серединой противоположной стороны
Угол, градусная мера которого меньше 90º
Луч, делящий угол пополам
Углы, образованные при пересечении двух прямых
Прямые, которые лежат на одной плоскости и никогда не пересекаются
Арифметическое действие
Угол, градусная мера которого больше 90º
Слайд 31Кроссворд
1.Единица измерения угла
Результат сложения
Четырехугольник, у которого все стороны равны и все
Результат вычитания
Угол, равный 90º
Четырехугольник, у которого все стороны равны
Сотая часть какого-нибудь числа
Отрезок, соединяющий вершины треугольника с серединой противоположной стороны
Угол, градусная мера которого меньше 90º
Луч, делящий угол пополам
Углы, образованные при пересечении двух прямых
Прямые, которые лежат на одной плоскости и никогда не пересекаются
Арифметическое действие
Угол, градусная мера которого больше 90º
Слайд 32Кроссворд
1.Единица измерения угла
Результат сложения
Четырехугольник, у которого все стороны равны и все
Результат вычитания
Угол, равный 90º
Четырехугольник, у которого все стороны равны
Сотая часть какого-нибудь числа
Отрезок, соединяющий вершины треугольника с серединой противоположной стороны
Угол, градусная мера которого меньше 90º
Луч, делящий угол пополам
Углы, образованные при пересечении двух прямых
Прямые, которые лежат на одной плоскости и никогда не пересекаются
Арифметическое действие
Угол, градусная мера которого больше 90º
Слайд 33Кроссворд
1.Единица измерения угла
Результат сложения
Четырехугольник, у которого все стороны равны и все
Результат вычитания
Угол, равный 90º
Четырехугольник, у которого все стороны равны
Сотая часть какого-нибудь числа
Отрезок, соединяющий вершины треугольника с серединой противоположной стороны
Угол, градусная мера которого меньше 90º
Луч, делящий угол пополам
Углы, образованные при пересечении двух прямых
Прямые, которые лежат на одной плоскости и никогда не пересекаются
Арифметическое действие
Угол, градусная мера которого больше 90º
Слайд 34Кроссворд
1.Единица измерения угла
Результат сложения
Четырехугольник, у которого все стороны равны и все
Результат вычитания
Угол, равный 90º
Четырехугольник, у которого все стороны равны
Сотая часть какого-нибудь числа
Отрезок, соединяющий вершины треугольника с серединой противоположной стороны
Угол, градусная мера которого меньше 90º
Луч, делящий угол пополам
Углы, образованные при пересечении двух прямых
Прямые, которые лежат на одной плоскости и никогда не пересекаются
Арифметическое действие
Угол, градусная мера которого больше 90º
Слайд 35Кроссворд
1.Единица измерения угла
Результат сложения
Четырехугольник, у которого все стороны равны и все
Результат вычитания
Угол, равный 90º
Четырехугольник, у которого все стороны равны
Сотая часть какого-нибудь числа
Отрезок, соединяющий вершины треугольника с серединой противоположной стороны
Угол, градусная мера которого меньше 90º
Луч, делящий угол пополам
Углы, образованные при пересечении двух прямых
Прямые, которые лежат на одной плоскости и никогда не пересекаются
Арифметическое действие
Угол, градусная мера которого больше 90º
Слайд 36Кроссворд
1.Единица измерения угла
Результат сложения
Четырехугольник, у которого все стороны равны и все
Результат вычитания
Угол, равный 90º
Четырехугольник, у которого все стороны равны
Сотая часть какого-нибудь числа
Отрезок, соединяющий вершины треугольника с серединой противоположной стороны
Угол, градусная мера которого меньше 90º
Луч, делящий угол пополам
Углы, образованные при пересечении двух прямых
Прямые, которые лежат на одной плоскости и никогда не пересекаются
Арифметическое действие
Угол, градусная мера которого больше 90º
Слайд 37Кроссворд
1.Единица измерения угла
Результат сложения
Четырехугольник, у которого все стороны равны и все
Результат вычитания
Угол, равный 90º
Четырехугольник, у которого все стороны равны
Сотая часть какого-нибудь числа
Отрезок, соединяющий вершины треугольника с серединой противоположной стороны
Угол, градусная мера которого меньше 90º
Луч, делящий угол пополам
Углы, образованные при пересечении двух прямых
Прямые, которые лежат на одной плоскости и никогда не пересекаются
Арифметическое действие
Угол, градусная мера которого больше 90º
Слайд 38Кроссворд
1.Единица измерения угла
Результат сложения
Четырехугольник, у которого все стороны равны и все
Результат вычитания
Угол, равный 90º
Четырехугольник, у которого все стороны равны
Сотая часть какого-нибудь числа
Отрезок, соединяющий вершины треугольника с серединой противоположной стороны
Угол, градусная мера которого меньше 90º
Луч, делящий угол пополам
Углы, образованные при пересечении двух прямых
Прямые, которые лежат на одной плоскости и никогда не пересекаются
Арифметическое действие
Угол, градусная мера которого больше 90º
Слайд 39Кроссворд
1.Единица измерения угла
Результат сложения
Четырехугольник, у которого все стороны равны и все
Результат вычитания
Угол, равный 90º
Четырехугольник, у которого все стороны равны
Сотая часть какого-нибудь числа
Отрезок, соединяющий вершины треугольника с серединой противоположной стороны
Угол, градусная мера которого меньше 90º
Луч, делящий угол пополам
Углы, образованные при пересечении двух прямых
Прямые, которые лежат на одной плоскости и никогда не пересекаются
Арифметическое действие
Угол, градусная мера которого больше 90º
Слайд 40Кроссворд
1.Единица измерения угла
Результат сложения
Четырехугольник, у которого все стороны равны и все
Результат вычитания
Угол, равный 90º
Четырехугольник, у которого все стороны равны
Сотая часть какого-нибудь числа
Отрезок, соединяющий вершины треугольника с серединой противоположной стороны
Угол, градусная мера которого меньше 90º
Луч, делящий угол пополам
Углы, образованные при пересечении двух прямых
Прямые, которые лежат на одной плоскости и никогда не пересекаются
Арифметическое действие
Угол, градусная мера которого больше 90º
Слайд 41Кроссворд
1.Единица измерения угла
Результат сложения
Четырехугольник, у которого все стороны равны и все
Результат вычитания
Угол, равный 90º
Четырехугольник, у которого все стороны равны
Сотая часть какого-нибудь числа
Отрезок, соединяющий вершины треугольника с серединой противоположной стороны
Угол, градусная мера которого меньше 90º
Луч, делящий угол пополам
Углы, образованные при пересечении двух прямых
Прямые, которые лежат на одной плоскости и никогда не пересекаются
Арифметическое действие
Угол, градусная мера которого больше 90º
Слайд 42Кроссворд
Единица измерения угла
Результат сложения
Четырехугольник, у которого все стороны равны и все
Результат вычитания
Угол, равный 90º
Четырехугольник, у которого все стороны равны
Сотая часть какого-нибудь числа
Отрезок, соединяющий вершины треугольника с серединой противоположной стороны
Угол, градусная мера которого меньше 90º
Луч, делящий угол пополам
Углы, образованные при пересечении двух прямых
Прямые, которые лежат на одной плоскости и никогда не пересекаются
Арифметическое действие
Угол, градусная мера которого больше 90º