- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад урока на конкурс Мой лучший урок
Содержание
- 1. Презентация урока на конкурс Мой лучший урок
- 2. Урок на тему «Теорема Пифагора»Автор:
- 3. I. Организационно – мотивационный этап урокаСоздание учебной
- 4. II. Актуализация знаний Прямоугольный
- 5. УУДРегулятивные: умение планировать своё действие в соответствии
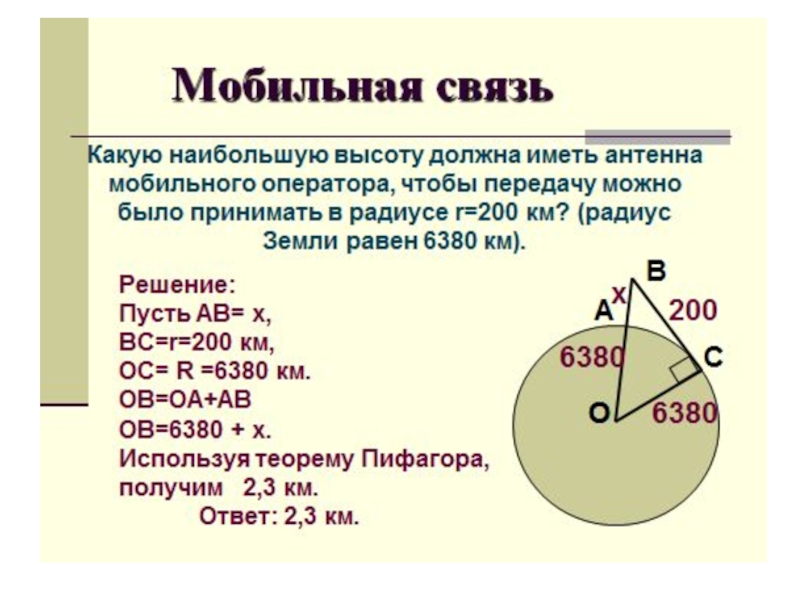
- 6. III. Постановка цели и задач урока. Видеоролик «Теорема Пифагора»Теорема Пифагора
- 7. Цель урока: Познакомиться с теоремой
- 8. УУДПознавательные: уметь видеть математическую задачу в контексте
- 9. IV. Открытие новых знаний. Теорема Пифагора:В
- 10. Доказательство1) Достроим треугольник до квадрата со стороной
- 11. Слайд 11
- 12. УУДРегулятивные: - планировать своё действие в
- 13. V. Физкультминутка
- 14. VI. Закрепление изученного материала Задача 143?ACBAB² =
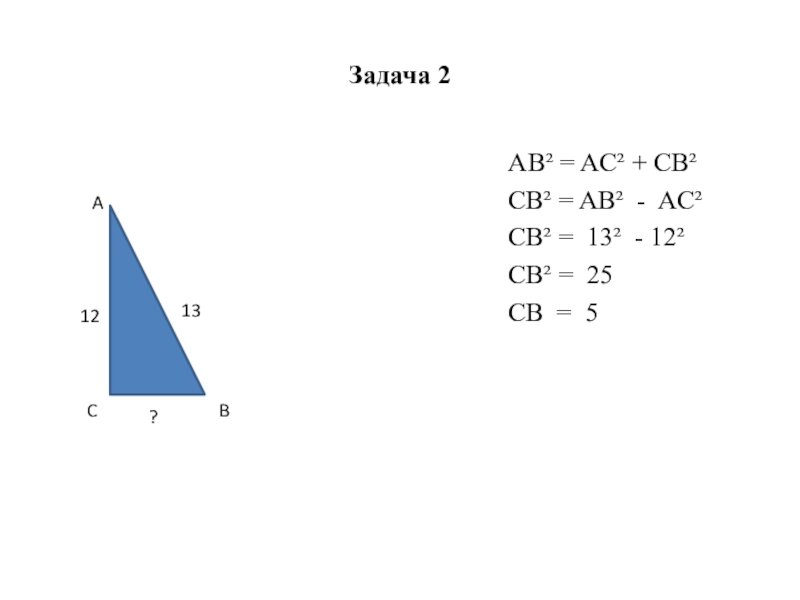
- 15. Задача 2ACB1312?AB² = AC² + CB²CB² =
- 16. VII. Самостоятельная работа вариант 1
- 17. Проверка самостоятельной работы:Вариант 1.1) AB² = AC²
- 18. УУДРегулятивные: - принимать и сохранять учебную задачу;
- 19. VIII. Работа в группахГруппа 1 (базовый уровень):
- 20. Слайд 20
- 21. Слайд 21
- 22. УУДРегулятивные: - принимать и сохранять учебную
- 23. IX. Домашнее задание:П. 55-читать,выучить теорему Пифагора (на
- 24. Итог урока:Какую задачу мы ставили на урок?Сформулируйте
- 25. Пребудет вечной истина, как скороЕё познает слабый
Слайд 1
Районный конкурс педагогического мастерства
«Мой лучший урок»
A
B
C
Учитель математики
МБОУ «Светловская СОШ
имени
Арапова Ольга Васильевна
Слайд 2Урок на тему «Теорема Пифагора»
Автор:
Направление: Основное общее образование.
Тип: Урок изучения нового материала.
Класс: 8 класс.
Характеристика Общеобразовательный класс с базовым и
класса: повышенным уровнем обученности.
Программа: Общеобразовательная программа.
Учебник: Геометрия 7-9 класс. / авторы Л. С. Атанасян, и
др. М.: Просвещение 2014г.
Количество 70 часов в год, 2 часа в неделю .
часов
Слайд 3I. Организационно – мотивационный этап урока
Создание учебной ситуации.
УУД:
Регулятивные: умение организовывать
Личностные: способность самооценки на основе критерия успешности учебной деятельности.
Слайд 4
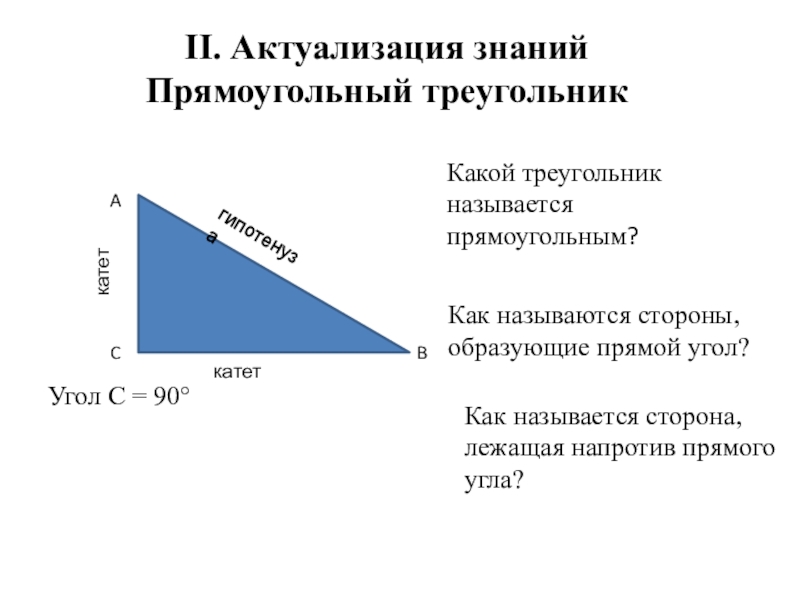
II. Актуализация знаний
Прямоугольный треугольник
Угол С = 90°
A
C
B
катет
катет
гипотенуза
Какой треугольник называется прямоугольным?
Как называются
образующие прямой угол?
Как называется сторона,
лежащая напротив прямого
угла?
Слайд 5УУД
Регулятивные: умение планировать своё действие в соответствии с поставленной задачей и
Коммуникативные: уметь формировать собственное мнение и позицию;
Познавательные: использовать знаково-символических средства;
Личностные:
умение ясно, точно, грамотно излагать свои мысли в устной и письменной речи;
понимать смысл поставленной задачи.
Слайд 7
Цель урока:
Познакомиться с теоремой Пифагора.
Научиться использовать теорему Пифагора при решении задач.
Найти применение теоремы Пифагора в реальной математике.
Слайд 8УУД
Познавательные: уметь видеть математическую задачу в контексте проблемной ситуации в окружающей
Регулятивные: уметь ставить, принимать и сохранять учебную задачу.
Личностные: уменясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи.
Коммуникативные:
- уметь формировать собственное мнение и позицию;
- умение вступать в диалог.
Слайд 9IV. Открытие новых знаний.
Теорема Пифагора:
В прямоугольном треугольнике квадрат гипотенузы равен
b
с
а
c² = a² + b²
Дано: прямоугольный
треугольник
a, b – катеты
с – гипотенуза.
Доказать: c² = a² + b²
Слайд 10Доказательство
1) Достроим треугольник до квадрата со стороной a + b.
2) Его площадь равна
S(АВСD) = (a + b)² [1]
3) С другой стороны этот квадрат состоит из четырех равных треугольников
S∆ = 1/2ab; 4S∆ = 4*1/2ab = 2ab
и квадрата со стороной с:
S(KPNM) = с²
Отсюда S(АВСD) = 2ab + c² [2]
4) Из [1] и [2] получим:
2ab+c² = (a+b)²
5) c²+2ab=a²+2ab+b²
6) c²=a²+b²
Что и требовалось доказать.
a
b
c
a
b
c
c
c
a
a
b
b
В
А
D
С
К
P
N
M
Слайд 12УУД
Регулятивные:
- планировать своё действие в соответствии с поставленной
задачей и условиями её реализации;
- понимать сущность алгоритмических предписаний и
уметь действовать в соответствии с предложенным
алгоритмом.
Личностные: умение ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи.
Коммуникативные: умеют выдвигать гипотезы и понимать необходимость их проверки.
Слайд 14VI. Закрепление изученного материала
Задача 1
4
3
?
A
C
B
AB² = AC² + CB²
AB² =
AB² = 25
AB = 5
Слайд 16VII. Самостоятельная работа вариант 1
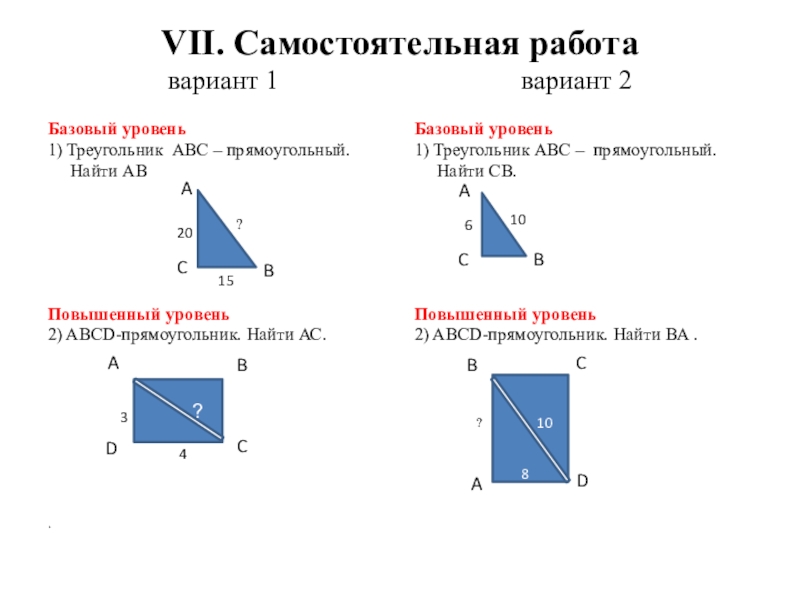
Базовый уровень
1) Треугольник АВС – прямоугольный.
Найти АВ
?
Повышенный уровень
2) ABCD-прямоугольник. Найти АС.
?
.
Базовый уровень
1) Треугольник АВС – прямоугольный.
Найти СВ.
?
Повышенный уровень
2) ABCD-прямоугольник. Найти BA .
?
?
C
A
B
A
D
B
C
C
A
B
A
B
C
D
20
15
4
3
6
10
10
8
Слайд 17Проверка самостоятельной работы:
Вариант 1.
1) AB² = AC² + CB²
AB²
AB² = 625
AB = 25
2) ∆ACD-прямоугольный
AC² = AD² + DC²
AC² = 4² + 3²
AC² = 25
AC = 5
Вариант 2
1) AB² = AC² + CB²
BC² = AB² - AC²
BC² = 10² - 6²
BC² = 64
BC = 8
2) ∆ BAD - прямоугольный
BA² = BD² - AD²
BA² = 10² - 8²
BA² = 36
BA = 6
Слайд 18УУД
Регулятивные: - принимать и сохранять учебную задачу;
- планировать своё
задачей и условиями её реализации;
- осуществлять самоконтроль.
Коммуникативные: - уметь формулировать собственное мнение и позицию;
Познавательные: - использование знаково-символических средств ;
- находить нужную информацию;
- умение осуществлять синтез как составление целого из частей;
- определять границы собственных знаний и незнаний.
Личностные: - умение ясно, точно, грамотно излагать свои мысли в устной и письменной речи,
- осознавать необходимость нового знания.
Слайд 19VIII. Работа в группах
Группа 1 (базовый уровень):
Точка крепления троса,
находится на высоте 8 м. от земли. Расстояние от основания флагштока до места крепления троса на земле равно 6 м. найдите длину троса.
Задание: - Какая геометрическая фигура получилась в результате?
- Найдите длину троса.
ГРУППА2 ( ПОВЫШЕННЫЙ УРОВЕНЬ)
Какова длина (в метрах) лестницы, которую прислонили к дереву, если верхний её конец находиться на высоте 3,5 м. над землёй, а нижний отстоит от ствола дерева на 1,2 м.
Задание: - Дочертите рисунок (изобразите лестницу, прислонённую к дереву до метки).
- Какая геометрическая фигура получилась в результате?
- Найдите длину лестницы.
ГРУППА2 ( ПОВЫШЕННЫЙ УРОВЕНЬ)
Слайд 22УУД
Регулятивные:
- принимать и сохранять учебную задачу;
-
задачей и условиями её реализации;
Коммуникативные:
- уметь договариваться и приходить к общему решению в
совместной деятельности;
- участвовать в коллективном обсуждении учебной проблемы.
Познавательные: уметь видеть математическую задачу в контексте проблемной ситуации в окружающей жизни .
Личностные: умение ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи.
Слайд 23IX. Домашнее задание:
П. 55-читать,выучить теорему Пифагора
(на «4» и «5» выучить
с.133 вопрос № 9, № 484(а, б) , 487
Творческое задание: приготовить сообщение на тему «Применение теоремы Пифагора в разных предметных областях»
УУД
Регулятивные:
- принимать и сохранять учебную задачу;
- планировать своё действие в соответствии с поставленной задачей и условиями её реализации;
Личностные: развитие познавательных интересов, учебных мотивов.
Слайд 24Итог урока:
Какую задачу мы ставили на урок?
Сформулируйте теорему Пифагора.
Достигли ли мы
Рефлексия
- Что нового вы открыли для себя на уроке?
- Где можно применить теорему Пифагора в жизни?