пос. Нового
Бархян Лилит
учитель Великая Лариса Ивановна
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад учащегося по теме:Треугольник (7 класс)
Содержание
- 1. Презентация учащегося по теме:Треугольник (7 класс)
- 2. Треугольником называется фигура, которая состоит из трёх
- 3. Виды треугольников Треугольник
- 4. Треугольник называется прямоугольным, если у него есть
- 5. Землемеры Древнего Египта для построения прямого угла использовали бечёвку, разделенную узлами на 12 равных частей.
- 6. Слайд 6
- 7. БиссектрисаБиссектриса угла — это луч, который
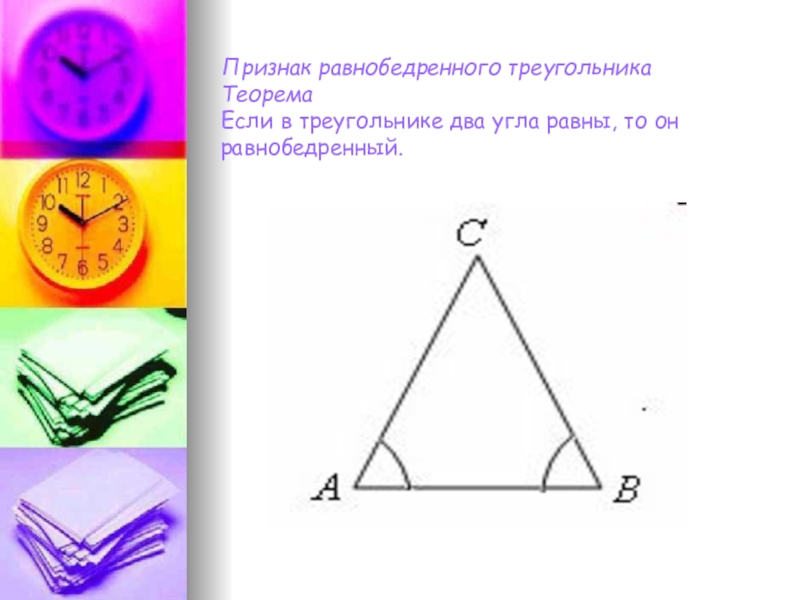
- 8. Признак равнобедренного треугольника Теорема Если в треугольнике два угла равны, то он равнобедренный.
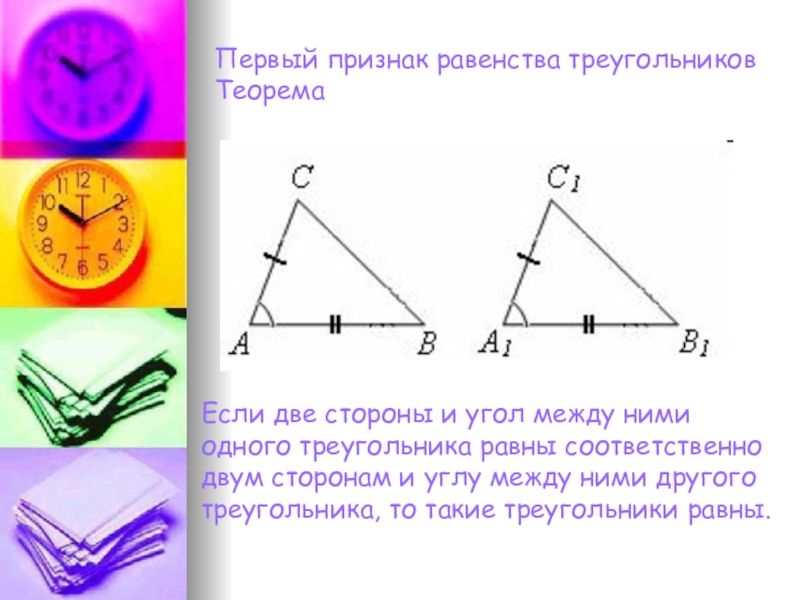
- 9. Первый признак равенства треугольников ТеоремаЕсли две стороны
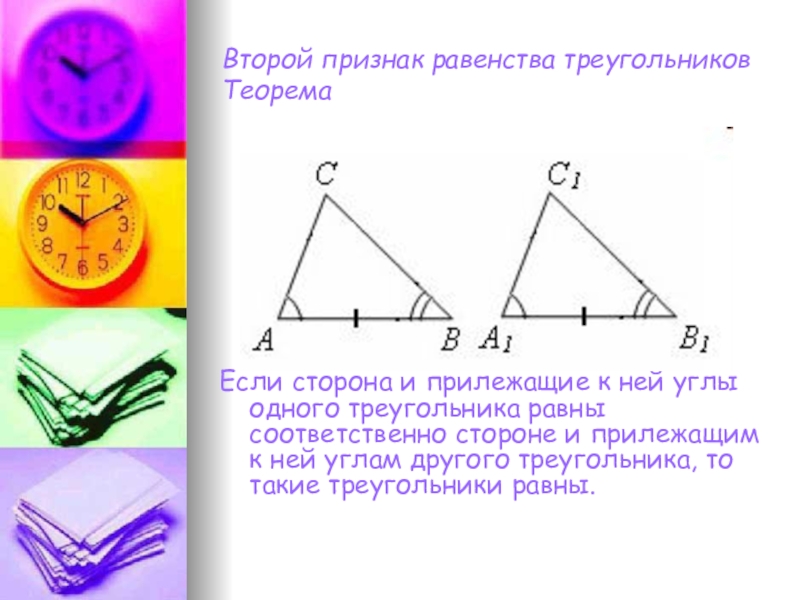
- 10. Второй признак равенства треугольников ТеоремаЕсли сторона и
- 11. Третий признак равенства треугольников
- 12. Спасибо за внимание
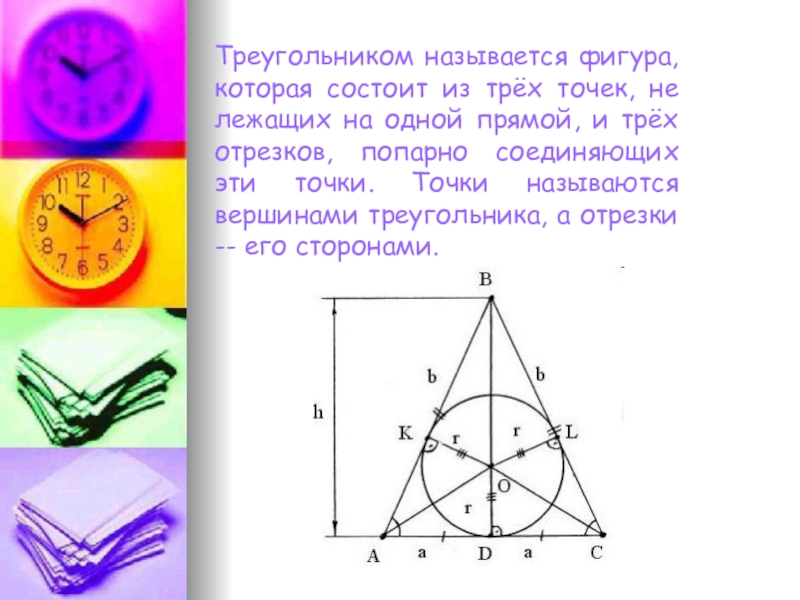
Треугольником называется фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки. Точки называются вершинами треугольника, а отрезки -- его сторонами.
Слайд 2Треугольником называется фигура, которая состоит из трёх точек, не лежащих на
одной прямой, и трёх отрезков, попарно соединяющих эти точки. Точки называются вершинами треугольника, а отрезки -- его сторонами.
Слайд 3 Виды треугольников Треугольник называется равнобедренным, если у
него две стороны равны. Эти равные стороны называются боковыми сторонами, а третья сторона называется основанием треугольника.
Треугольник, у которого все стороны равны, называется равносторонним или правильным.
Слайд 4Треугольник называется прямоугольным, если у него есть прямой угол, то есть
угол в 90°. Сторона прямоугольного треугольника, противолежащая прямому углу, называется гипотенузой, две другие стороны называются катетами.
Треугольник называется остроугольным, если все три его угла — острые, то есть меньше 90°.
Треугольник называется тупоугольным, если один из его углов — тупой, то есть больше 90°.
Треугольник называется остроугольным, если все три его угла — острые, то есть меньше 90°.
Треугольник называется тупоугольным, если один из его углов — тупой, то есть больше 90°.
Слайд 5Землемеры Древнего Египта для построения прямого угла использовали бечёвку, разделенную узлами
на 12 равных частей.
Слайд 6 Медиана
Медиана треугольника
— это отрезок, соединяющий вершину треугольника с серединой противолежащей стороны этого треугольника.
Свойства медиан треугольника
Медиана разбивает треугольник на два треугольника одинаковой площади.
Медианы треугольника пересекаются в одной точке, которая делит каждую из них в отношении 2:1, считая от вершины. Эта точка называется центром тяжести треугольника.
Весь треугольник разделяется своими медианами на шесть равновеликих треугольников.
Свойства медиан треугольника
Медиана разбивает треугольник на два треугольника одинаковой площади.
Медианы треугольника пересекаются в одной точке, которая делит каждую из них в отношении 2:1, считая от вершины. Эта точка называется центром тяжести треугольника.
Весь треугольник разделяется своими медианами на шесть равновеликих треугольников.
Слайд 7 Биссектриса
Биссектриса угла — это луч, который исходит из его вершины,
проходит между его сторонами и делит данный угол пополам. Биссектрисой треугольника называется отрезок биссектрисы угла треугольника, соединяющий вершину с точкой на противолежащей стороне этого треугольника.
Свойства биссектрис треугольника
Биссектриса угла — это геометрическое место точек, равноудаленных от сторон этого угла.
Биссектриса внутреннего угла треугольника делит противолежащую сторону на отрезки, пропорциональные прилегающим сторонам: .
Точка пересечения биссектрис треугольника является центром окружности, вписанной в этот треугольник.
Свойства биссектрис треугольника
Биссектриса угла — это геометрическое место точек, равноудаленных от сторон этого угла.
Биссектриса внутреннего угла треугольника делит противолежащую сторону на отрезки, пропорциональные прилегающим сторонам: .
Точка пересечения биссектрис треугольника является центром окружности, вписанной в этот треугольник.
Слайд 8Признак равнобедренного треугольника Теорема Если в треугольнике два угла равны, то он
равнобедренный.
Слайд 9Первый признак равенства треугольников
Теорема
Если две стороны и угол между ними одного
треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
Слайд 10Второй признак равенства треугольников
Теорема
Если сторона и прилежащие к ней углы одного
треугольника равны соответственно стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны.
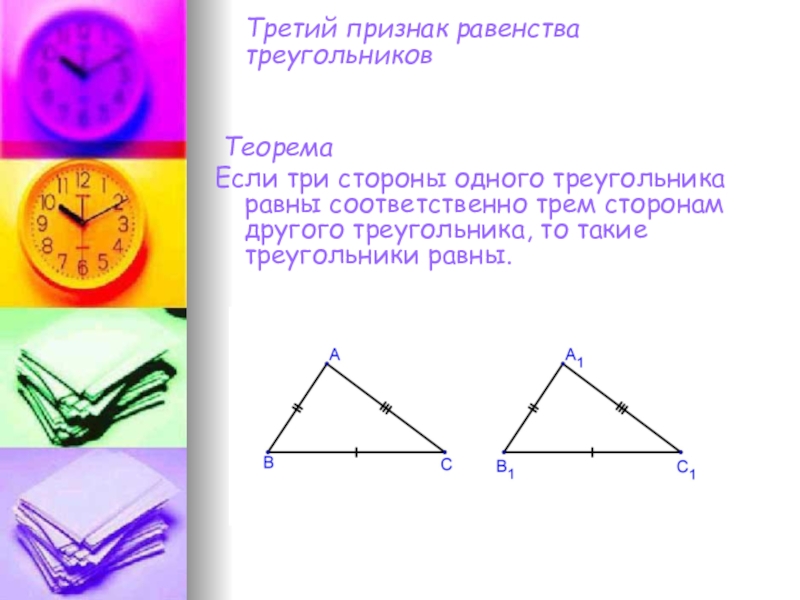
Слайд 11 Третий признак равенства треугольников
Теорема
Если
три стороны одного треугольника равны соответственно трем сторонам другого треугольника, то такие треугольники равны.