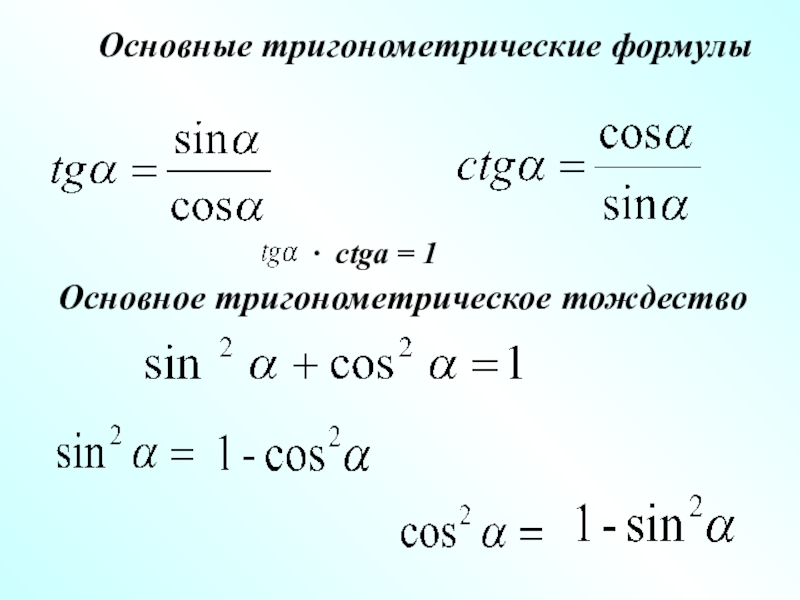семь раз больше того, кому все разъясняется.
Артур Гитерман.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Тригонометрические функции (8 класс)
Содержание
- 1. Презентация Тригонометрические функции (8 класс)
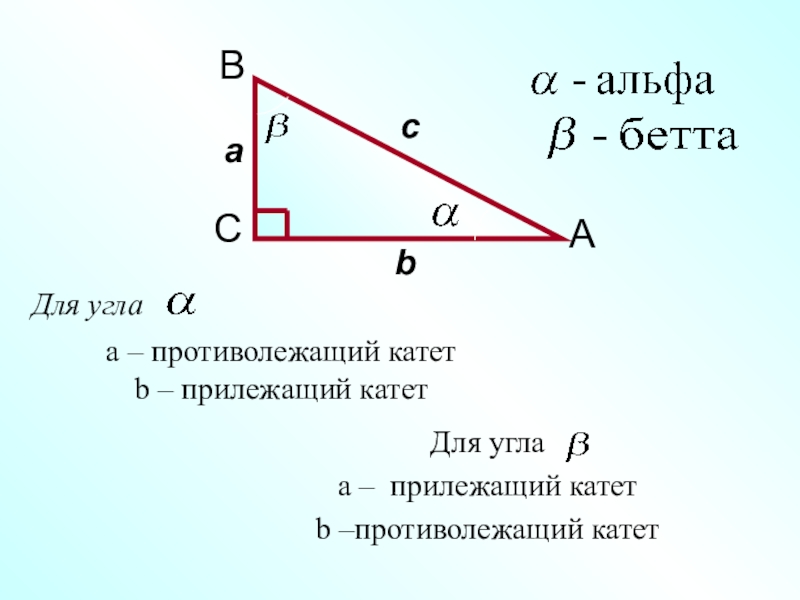
- 2. Для угла a – противолежащий катет b – прилежащий катетДля углаa – прилежащий катетb –противолежащий катет
- 3. Для вычисления неизвестных элементов (сторон и
- 4. Определения: Синусом острого угла прямоугольного треугольника называется отношение
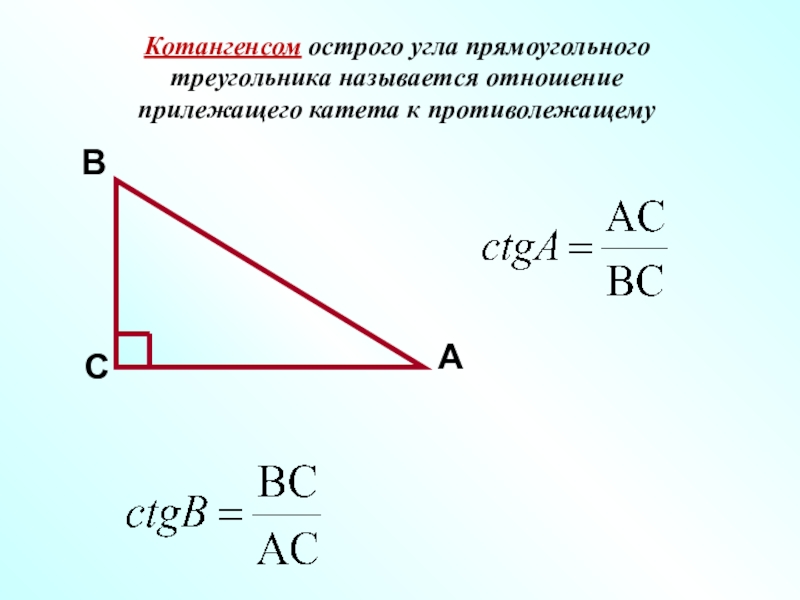
- 5. Котангенсом острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему
- 6. Историческая справкаОпределенияТождестваСлово «синус» появилось в математике далеко
- 7. Историческая справкаОпределенияТождестваТригонометрия - слово греческое и в
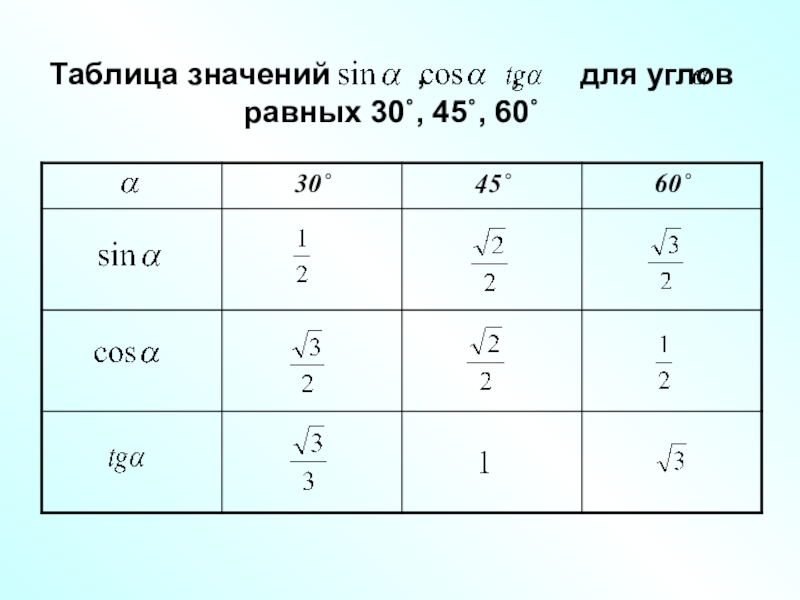
- 8. Таблица значений ,
- 9. Основные тригонометрические формулыОсновное тригонометрическое тождество· ctga = 1
- 10. Домашнее задание:§ 17 (правила, таблица)№ 582, 584
Для угла a – противолежащий катет b – прилежащий катетДля углаa – прилежащий катетb –противолежащий катет
Слайд 1Тригонометрические функции острого угла прямоугольного треугольника
Тот, кто учится самостоятельно, достигнет в
Слайд 2Для угла
a – противолежащий катет
b – прилежащий катет
Для угла
a –
прилежащий катет
b –противолежащий катет
b –противолежащий катет
Слайд 3 Для вычисления неизвестных элементов (сторон и углов)прямоугольного треугольника используют определения синуса,
косинуса, тангенса и котангенса острого угла:
Слайд 4Определения:
Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе
Косинусом
острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе
Тангенсом острого угла прямоугольного
треугольника называется отношение
противолежащего катета к прилежащему
Тангенсом острого угла прямоугольного
треугольника называется отношение
противолежащего катета к прилежащему
Слайд 5Котангенсом острого угла прямоугольного
треугольника называется отношение
прилежащего катета к противолежащему
Слайд 6Историческая справка
Определения
Тождества
Слово «синус» появилось в математике далеко не сразу. В работах
греческих астрономов встречается величина «хорда», что значит «струна». В V в. этот термин попал в Индию, где был переведен на местный научный язык санскрит, как «джива» - «тетива лука». В VIII в. в переводах индийских работ на арабский язык слово «джива» было переведено как «джайб», что означало «впадина». В XII в. арабские математические книги стали переводить на латинский язык, и «джайб» («впадина») было переведено словом «синус». «Косинус» – это сокращение латинского выражения completely sinus, т. е. «дополнительный синус» (или иначе «синус дополнительной дуги»).
Название «тангенс» появилось в XVI в., также имеет латинские корни и переводится как «касающийся».
Название «тангенс» появилось в XVI в., также имеет латинские корни и переводится как «касающийся».
Слайд 7Историческая справка
Определения
Тождества
Тригонометрия - слово греческое и в буквальном переводе означает измерение
треугольников.
В данном случае измерение треугольников следует понимать как решение треугольников, т.е. определение сторон, углов и других элементов треугольника, если даны некоторые из них.
Возникновение тригонометрии связано с землеизмерением, астрономией и строительным делом. Впервые способы решения треугольников, основанные на зависимостях между сторонами и углами треугольника, были найдены древнегреческими астрономами Гиппархом и Клавдием Птолемеем (2в. н.э.)
В данном случае измерение треугольников следует понимать как решение треугольников, т.е. определение сторон, углов и других элементов треугольника, если даны некоторые из них.
Возникновение тригонометрии связано с землеизмерением, астрономией и строительным делом. Впервые способы решения треугольников, основанные на зависимостях между сторонами и углами треугольника, были найдены древнегреческими астрономами Гиппархом и Клавдием Птолемеем (2в. н.э.)