- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Теорема Пифагора 8 класс
Содержание
- 1. Презентация Теорема Пифагора 8 класс
- 2. Теорема ПифагораПребудет вечной истина, как скороЕё познает
- 3. Содержание Формулировка теоремы Доказательства теоремы Значение теоремы Пифагора
- 4. Формулировка теоремы« Доказать, что квадрат, построенный
- 5. Современная формулировка« В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов».
- 6. Доказательства теоремы Существует около 500 различных доказательств этой теоремы (геометрических, алгебраических, механических и т.д.).
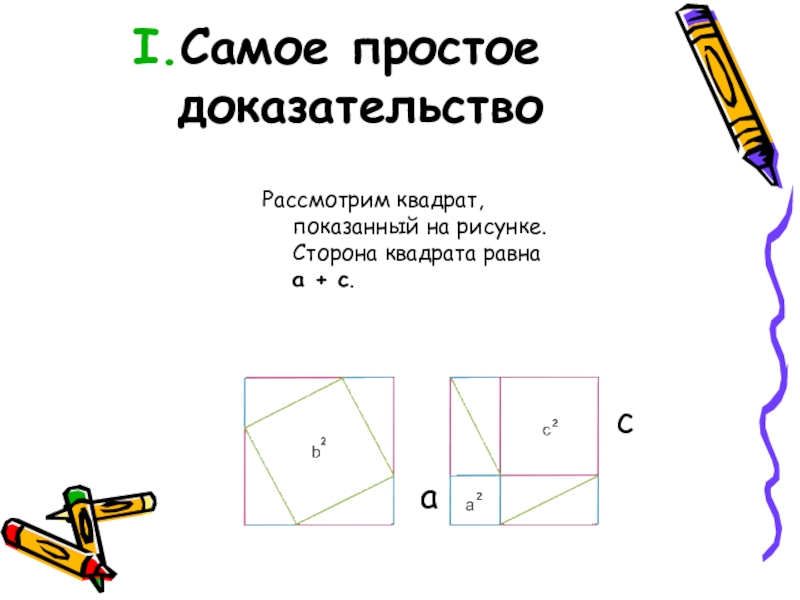
- 7. Самое простое доказательствоРассмотрим квадрат, показанный на рисунке. Сторона квадрата равна a + c. ca
- 8. В одном случае (слева) квадрат
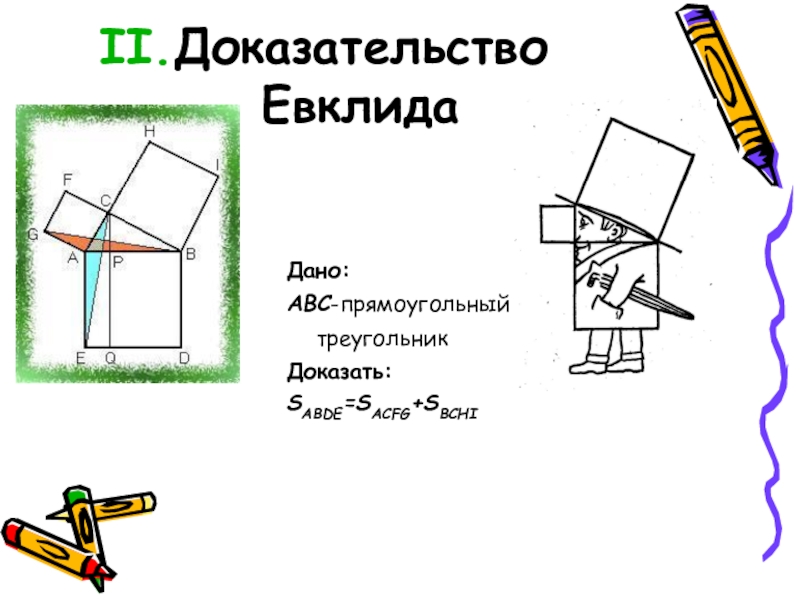
- 9. Доказательство Евклида Дано: ABC-прямоугольный треугольник Доказать:SABDE=SACFG+SBCHI
- 10. Доказательство: Пусть ABDE-квадрат, построенный на гипотенузе прямоугольного
- 11. Очевидно, что углы CAE=GAB(=A+90°); отсюда следует, что
- 12. Алгебраическое доказательствоДано: ABC-прямоугольный треугольникДоказать: AB2=AC2+BC2 Доказательство: 1) Проведем высоту
- 13. Геометрическое доказательство Дано: ABC-прямоугольный треугольникДоказать: BC2=AB2+AC2Доказательство: 1) Построим
- 14. Значение теоремы ПифагораТеорема Пифагора- это одна
- 15. Доказательство теоремы Пифагора учащиеся средних веков считали
Слайд 2Теорема Пифагора
Пребудет вечной истина, как скоро
Её познает слабый человек!
И ныне теорема
Верна, как и в его далёкий век.
Слайд 4Формулировка
теоремы
« Доказать, что квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик
« Площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на его катетах».
Во времена Пифагора теорема звучала так:
или
Слайд 5Современная формулировка
« В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов».
Слайд 6Доказательства теоремы
Существует около 500 различных доказательств этой теоремы (геометрических,
Слайд 7Самое простое доказательство
Рассмотрим квадрат, показанный на рисунке.
Сторона квадрата равна a +
c
a
Слайд 8
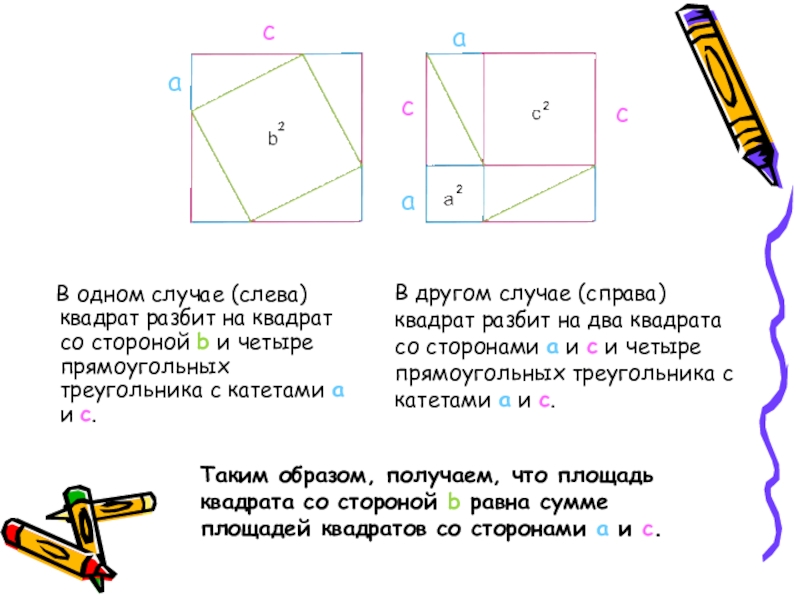
В одном случае (слева) квадрат разбит на квадрат со
a
c
a
c
В другом случае (справа) квадрат разбит на два квадрата со сторонами a и c и четыре прямоугольных треугольника с катетами a и c.
a
c
Таким образом, получаем, что площадь квадрата со стороной b равна сумме площадей квадратов со сторонами a и c.
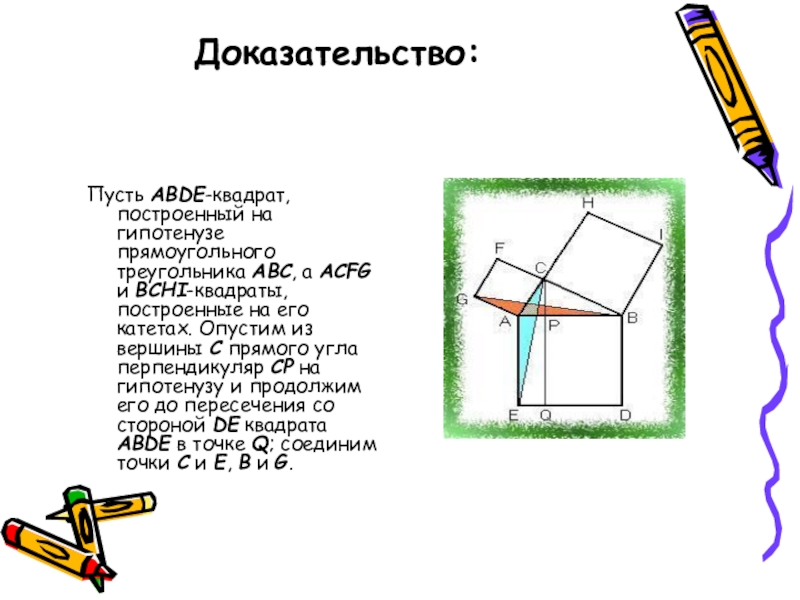
Слайд 10Доказательство:
Пусть ABDE-квадрат, построенный на гипотенузе прямоугольного треугольника ABC, а ACFG
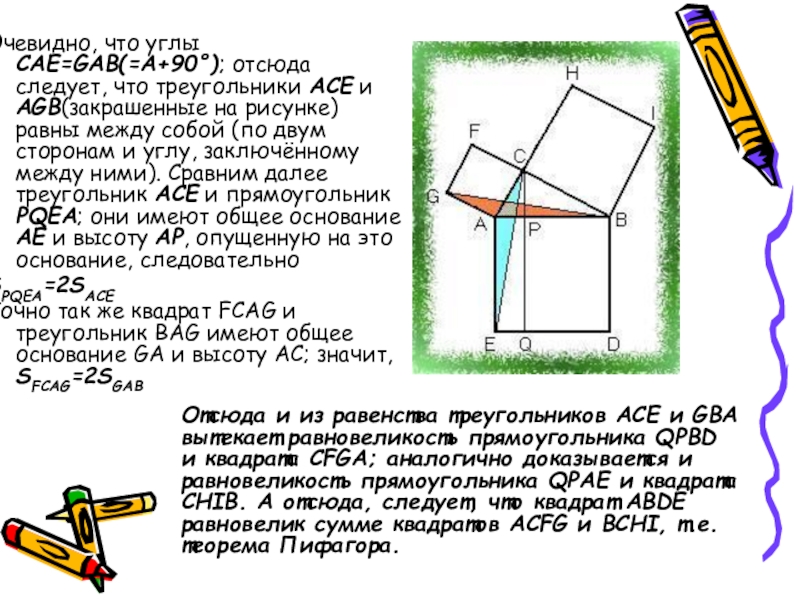
Слайд 11Очевидно, что углы CAE=GAB(=A+90°); отсюда следует, что треугольники ACE и AGB(закрашенные
SPQEA=2SACE
Точно так же квадрат FCAG и треугольник BAG имеют общее основание GA и высоту AC; значит, SFCAG=2SGAB
Отсюда и из равенства треугольников ACE и GBA вытекает равновеликость прямоугольника QPBD и квадрата CFGA; аналогично доказывается и равновеликость прямоугольника QPAE и квадрата CHIB. А отсюда, следует, что квадрат ABDE равновелик сумме квадратов ACFG и BCHI, т.е. теорема Пифагора.
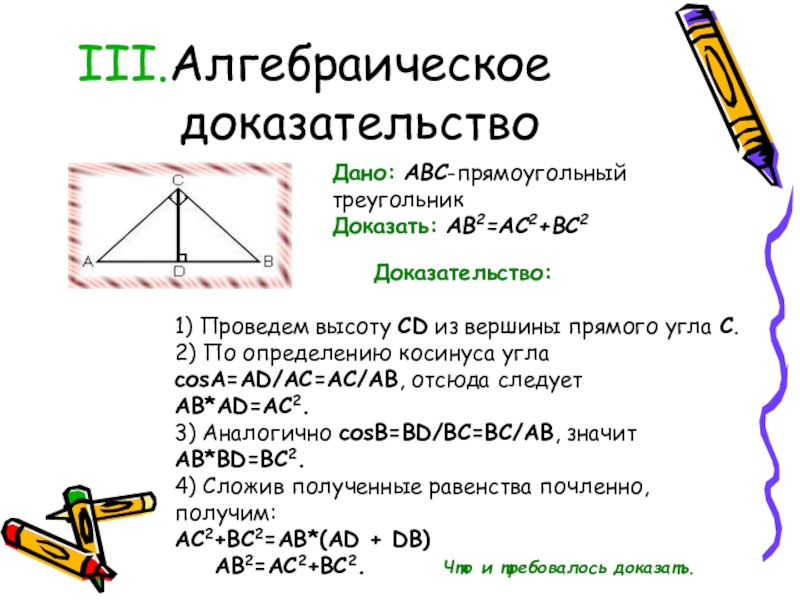
Слайд 12Алгебраическое доказательство
Дано: ABC-прямоугольный треугольник
Доказать: AB2=AC2+BC2
Доказательство:
1) Проведем высоту CD из вершины прямого угла
AB*AD=AC2.
3) Аналогично соsВ=BD/BC=BC/AB, значит
AB*BD=BC2.
4) Сложив полученные равенства почленно, получим:
AC2+BC2=АВ*(AD + DB)
AB2=AC2+BC2. Что и требовалось доказать.
Слайд 13Геометрическое доказательство
Дано: ABC-прямоугольный треугольник
Доказать: BC2=AB2+AC2
Доказательство:
1) Построим отрезок CD равный отрезку AB
SABED=2*AB*AC/2+BC2/2
3) Фигура ABED является трапецией, значит, её площадь равна:
SABED= (DE+AB)*AD/2.
4) Если приравнять левые части найденных выражений, то получим:
AB*AC+BC2/2=(DE+AB)(CD+AC)/2
AB*AC+BC2/2= (AC+AB)2/2
AB*AC+BC2/2= AC2/2+AB2/2+AB*AC
BC2=AB2+AC2.
Это доказательство было опубликовано в 1882 году Гэрфилдом.