- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Тема: Решение задач по теме Равнобедренный треугольник в 7 классе.
Содержание
- 1. Презентация Тема: Решение задач по теме Равнобедренный треугольник в 7 классе.
- 2. Цель: Закрепить теоретические знания по изучаемой теме.
- 3. Да, путь познания не гладок.Но знаем мы
- 4. Какой треугольник называется равнобедренным? Где в жизни встречается?
- 5. 1 вариант.Отрезок соединяющий верншну треугольника с серединой противоположной
- 6. 2 вариант.Высота равнобедренного треугольника, проведённая к основанию, является
- 7. 1 вариант.Отрезок соединяющий верншну треугольника с серединой противоположной
- 8. 2 вариант.Высота равнобедренного треугольника, проведённая к основанию, является
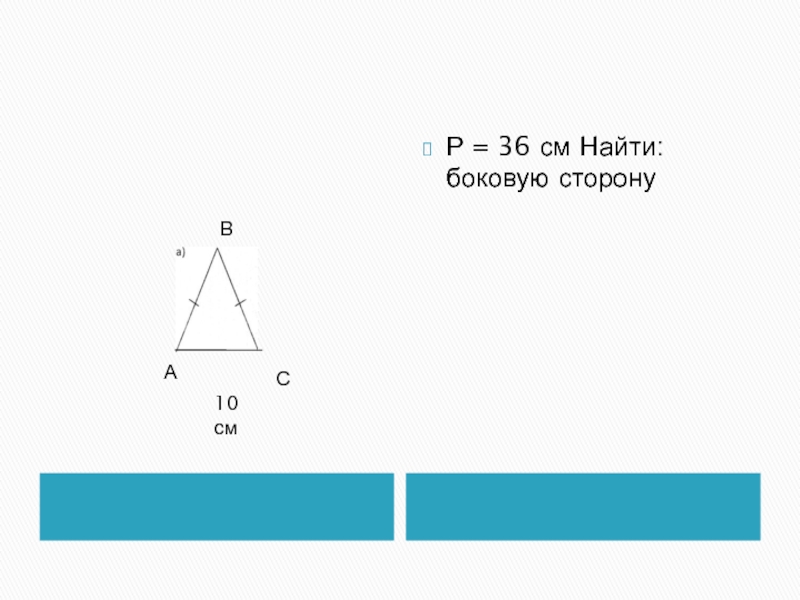
- 9. Р = 36 см Найти: боковую сторону10 смАСВ
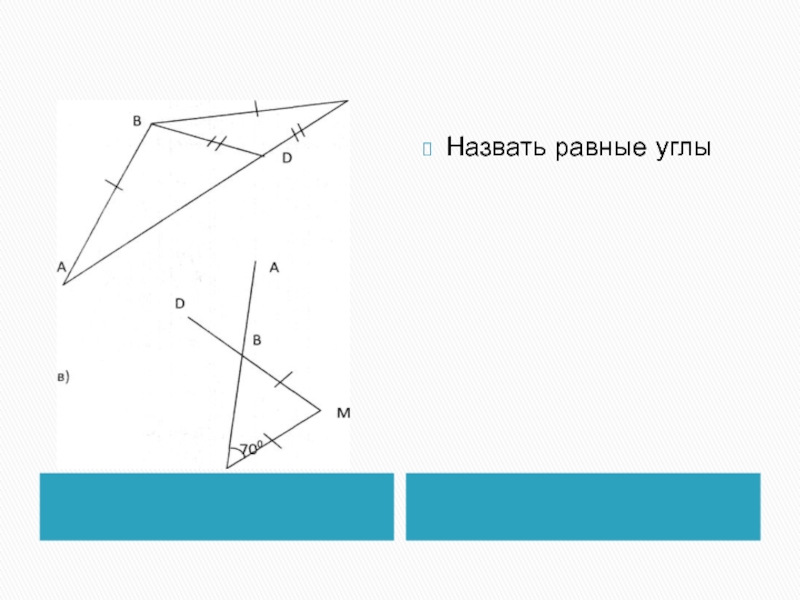
- 10. Назвать равные углы
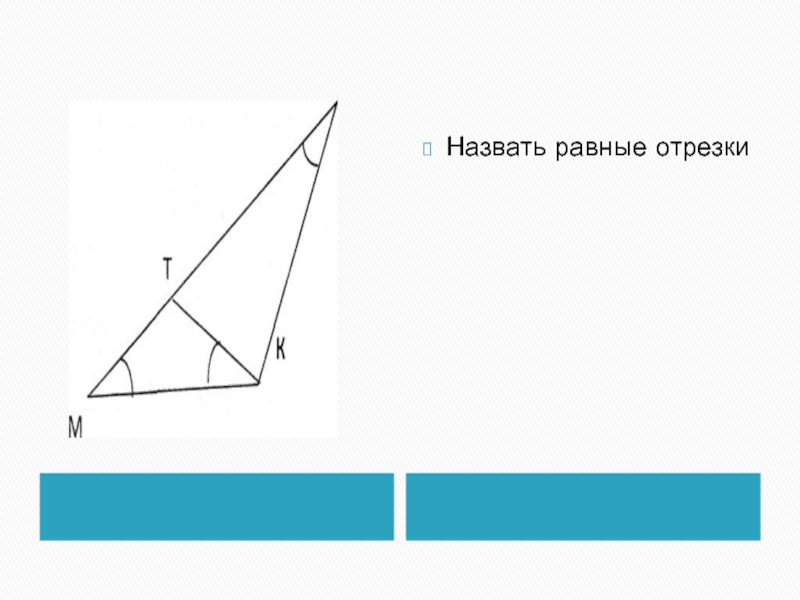
- 11. Назвать равные отрезки
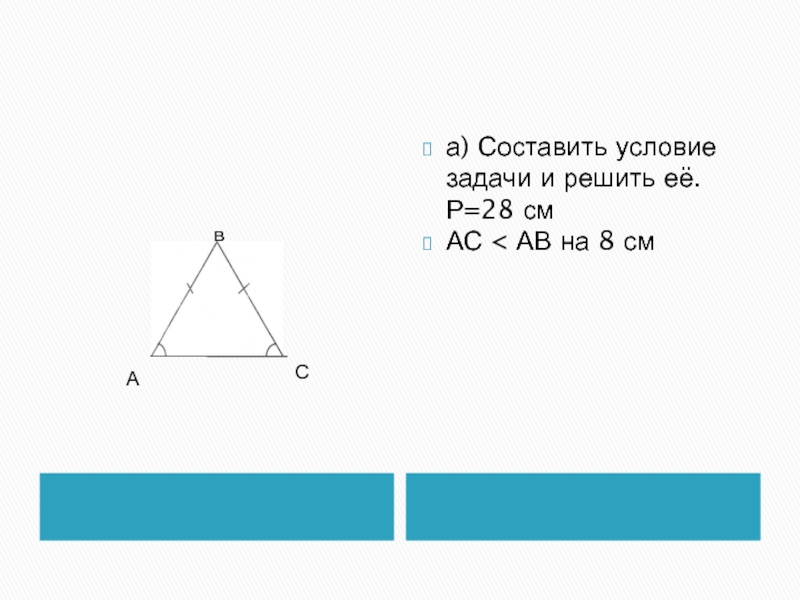
- 12. а) Составить условие задачи и решить её. Р=28 см АС < АВ на 8 смвАС
- 13. Проверяем!Решение: АВС - равнобедренный, т.к. два угла
- 14. Проверяем!В равнобедренном треугольнике АВС, с основанием АС,
- 15. Дополнительная задачаБоковая сторона равнобедренного треугольника в
- 16. Проверяем!Боковая сторона равнобедренного треугольника в 3 раза
- 17. Какой треугольник называется равнобедренным?Перечислить свойства равнобедренного треугольника. Ответьте на вопросы
Цель: Закрепить теоретические знания по изучаемой теме. Задачи: Совершенствовать навыки рения задач. Развивать логическое мышление, творческие способности учащихся. Воспитывать графическую культуру учащихся.
Слайд 2Цель: Закрепить теоретические знания по изучаемой теме.
Задачи:
Совершенствовать навыки рения
задач.
Развивать логическое мышление, творческие способности учащихся.
Воспитывать графическую культуру учащихся.
Развивать логическое мышление, творческие способности учащихся.
Воспитывать графическую культуру учащихся.
Слайд 3Да, путь познания не гладок.
Но знаем мы со школьных лет,
Загадок
больше чем разгадок
И поискам предела нет!
И поискам предела нет!
Эпиграф:
Слайд 51 вариант.
Отрезок соединяющий верншну треугольника с серединой противоположной
стороны, называется________ треугольника.
В треугольнике биссектриса, приведённая к
основанию, является
________ и__________ .
Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны, называется____________ треугольника.
В_________ треугольнике углы при основании равны.
Треугольник, у которого все стороны равны, называется_____________ .
________ и__________ .
Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны, называется____________ треугольника.
В_________ треугольнике углы при основании равны.
Треугольник, у которого все стороны равны, называется_____________ .
Слайд 62 вариант.
Высота равнобедренного треугольника, проведённая к основанию, является
____________ и___________ .
Треугольник, у которого две стороны
равны, назывется_____________ .
3. _______________ , проведенный из вершины треугольника к прямой,содержащей противоположнУю сторону треугольника, называется высотой.
В равнобедренном треугольнике медиана, проведённая к основанию является ____________ и ______________ .
Сторона равнобедренного треугольника, неравная двум другим его сторонам, называется _____________
3. _______________ , проведенный из вершины треугольника к прямой,содержащей противоположнУю сторону треугольника, называется высотой.
В равнобедренном треугольнике медиана, проведённая к основанию является ____________ и ______________ .
Сторона равнобедренного треугольника, неравная двум другим его сторонам, называется _____________
Слайд 71 вариант.
Отрезок соединяющий верншну треугольника с серединой противоположной
стороны, называется МЕДИАНОЙ треугольника.
В РАВНОБЕДРЕННОМ треугольнике биссектриса,
приведённая к основанию, является
МЕДИАНОЙ и ВЫСОТОЙ .
Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны, называется БИССЕКТРИССОЙ треугольника.
В РАВНОБЕДРЕННОМ треугольнике углы при основании равны.
Треугольник, у которого все стороны равны, называется РАВНОСТОРОННИМ .
МЕДИАНОЙ и ВЫСОТОЙ .
Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны, называется БИССЕКТРИССОЙ треугольника.
В РАВНОБЕДРЕННОМ треугольнике углы при основании равны.
Треугольник, у которого все стороны равны, называется РАВНОСТОРОННИМ .
ПРОВЕРЯЕМ!
Слайд 82 вариант.
Высота равнобедренного треугольника, проведённая к основанию, является
МЕДИАНОЙ и ВЫСОТОЙ .
Треугольник, у которого две
стороны равны, назывется РАВНОБЕДРЕННЫМ .
3. Перпендикуляр , проведенный из вершины треугольника к прямой,
содержащей противоположную сторону треугольника, называется высотой.
В равнобедренном треугольнике медиана, проведённая к основанию является высотой и биссектрисой .
Сторона равнобедренного треугольника, неравная двум другим его сторонам, называется основанием
3. Перпендикуляр , проведенный из вершины треугольника к прямой,
содержащей противоположную сторону треугольника, называется высотой.
В равнобедренном треугольнике медиана, проведённая к основанию является высотой и биссектрисой .
Сторона равнобедренного треугольника, неравная двум другим его сторонам, называется основанием
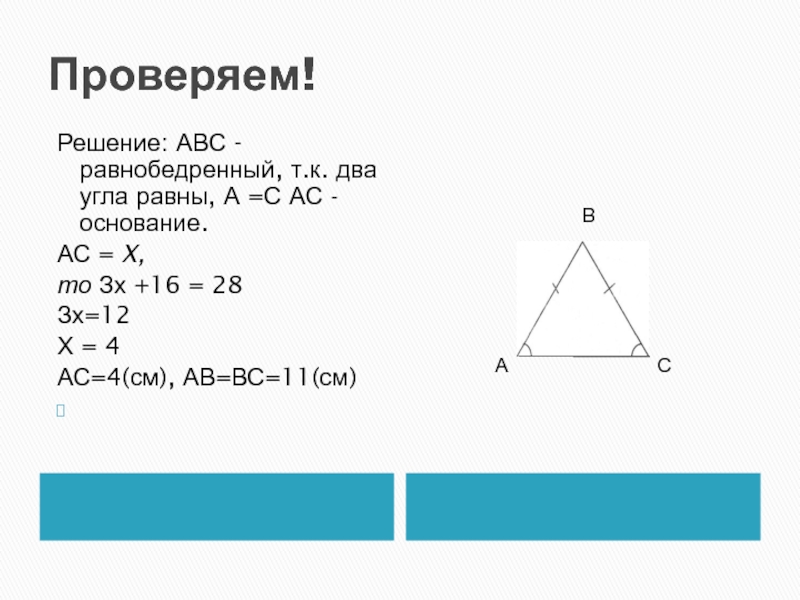
Слайд 13Проверяем!
Решение: АВС - равнобедренный, т.к. два угла равны, А =С АС
- основание.
АС = X,
то Зх +16 = 28
Зх=12
Х = 4
АС=4(см), АВ=ВС=11(см)
АС = X,
то Зх +16 = 28
Зх=12
Х = 4
АС=4(см), АВ=ВС=11(см)
В
А
С
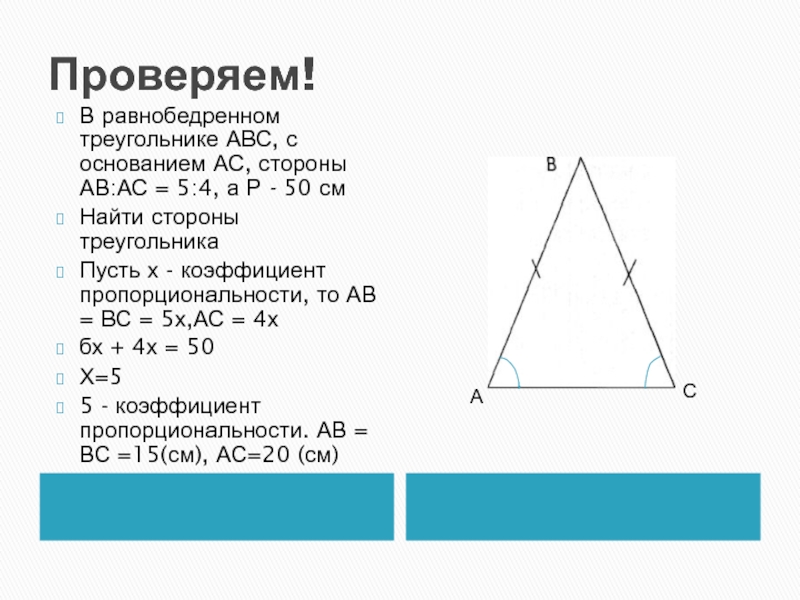
Слайд 14Проверяем!
В равнобедренном треугольнике АВС, с основанием АС, стороны АВ:АС = 5:4,
а Р - 50 см
Найти стороны треугольника
Пусть х - коэффициент пропорциональности, то АВ = ВС = 5х,АС = 4х
бх + 4х = 50
Х=5
5 - коэффициент пропорциональности. АВ = ВС =15(см), АС=20 (см)
Найти стороны треугольника
Пусть х - коэффициент пропорциональности, то АВ = ВС = 5х,АС = 4х
бх + 4х = 50
Х=5
5 - коэффициент пропорциональности. АВ = ВС =15(см), АС=20 (см)
А
С
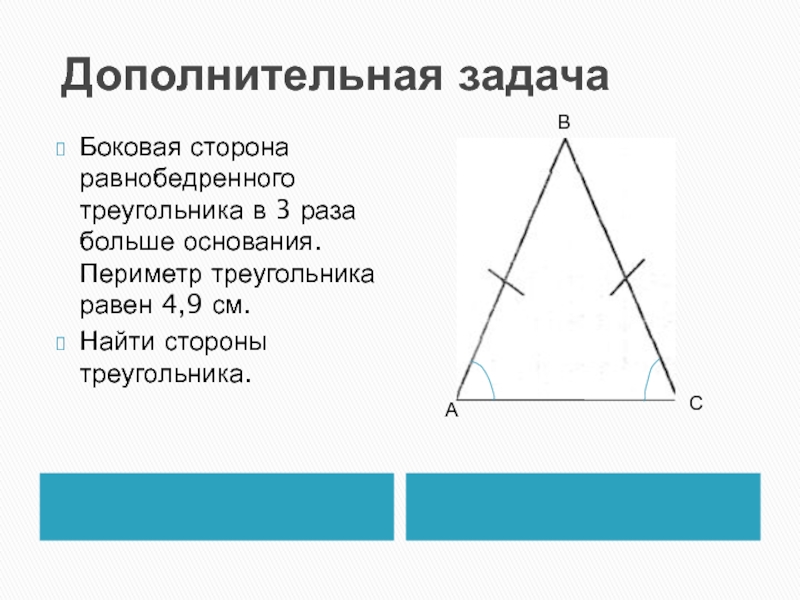
Слайд 15 Дополнительная задача
Боковая сторона равнобедренного треугольника в 3 раза больше основания.
Периметр треугольника равен 4,9 см.
Найти стороны треугольника.
Найти стороны треугольника.
В
А
С
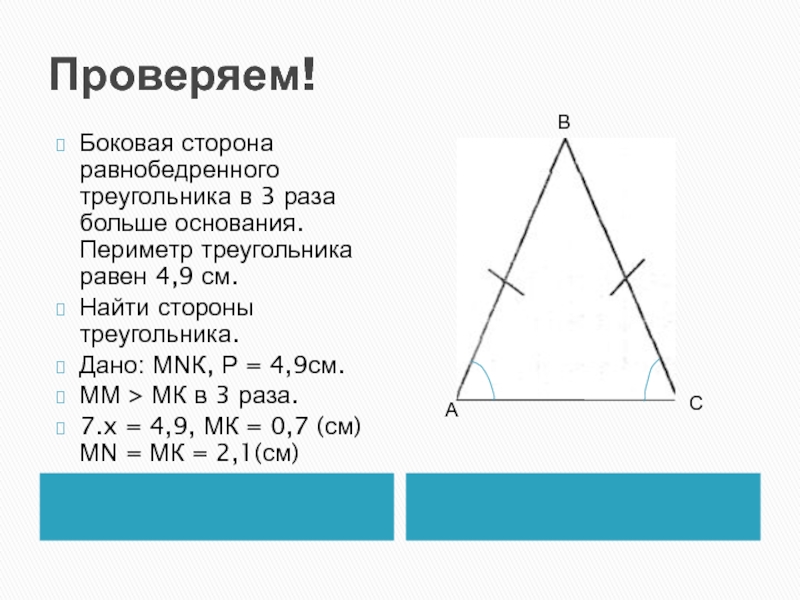
Слайд 16Проверяем!
Боковая сторона равнобедренного треугольника в 3 раза больше основания. Периметр треугольника
равен 4,9 см.
Найти стороны треугольника.
Дано: МNК, Р = 4,9см.
ММ > МК в 3 раза.
7.x = 4,9, МК = 0,7 (см) МN = МК = 2,1(см)
Найти стороны треугольника.
Дано: МNК, Р = 4,9см.
ММ > МК в 3 раза.
7.x = 4,9, МК = 0,7 (см) МN = МК = 2,1(см)
В
А
С
Слайд 17Какой треугольник называется равнобедренным?
Перечислить свойства равнобедренного треугольника.
Ответьте на вопросы
