Презентация, доклад Тайны числа ПИ

по вычислению приближенного значения отношения длины окружности к диаметру.
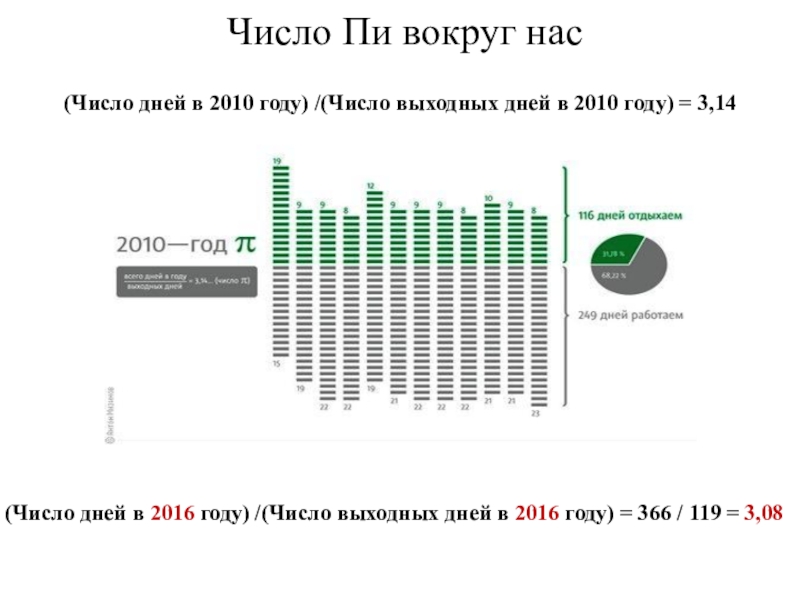
4) Рассмотреть некоторые факты из «современной биографии» числа π. .

На историческом материале показать важность проблемы вычисления числа π, раскрыть необходимость точных вычислений значения π на современном этапе,
а также показать огромное трудолюбие и работоспособность учёных, занимавшихся этим вопросом в течение многих столетий.

Цели:

Задачи:

знаменитым никогда не кончающимся числовым рядом. Во многих областях математики и физики ученые используют это число и его законы.

Мало какому числу из всех чисел, которые используются в математике, в естественных науках, в инженерном деле и в повседневной жизни, уделяется столько внимания, сколько уделяется числу π («пи»). В одной книге говорится: «Число π захватывает умы гениев науки и математиков-любителей во всем мире» («Fractals for the Classroom»).

Введение

ее диаметра.

Если принять диаметр окружности за единицу, то длина окружности
и есть число π.

В цифровом выражении π начинается как 3,141592 и имеет бесконечную математическую продолжительность.

Определение

течение которого π изучалось с позиции геометрии

2. Классическая эра, последовавшая за развитием математического анализа в Европе в XVII веке

3. Эра цифровых компьютеров.

заметили, что для того, чтобы получить корзину нужного диаметра, необходимо брать прутья в 3 раза длиннее его.

Найдены таблички из обожженной глины в Месопотамии, на которых зафиксирован данный факт.  

для построения квадрата,
равного по площади кругу:
« Отбрось от диаметра его девятую часть
и построй квадрат со стороной, равной остальной части, будет он эквивалентен кругу»
Из этого следует, что у Ахмеса π ≈ 3,1605.

Так началась письменная история числа π:

Ариабхаты (5-6 век).

Прибавь 4 к сотне и умножь на 8,
Потом ещё 62 000 прибавь.
Когда поделишь результат на 20 000,
Тогда откроется тебе значенье
Длины окружности к двум радиусам отношенье.

"Измерение круга“ следующее положение:
Отношение любой окружности к её диаметру меньше 3 целых1/7 и больше 3 целых 10/71.

верными знаками

правильными десятичными знаками, сделав 16 удвоений
числа сторон многоугольников

у английского математика Уильяма Джонса (1706г.),

а после опубликования работы Леонарда Эйлера (1736г. С.-Петербург), вычислившего значение π
с точностью до 153 десятичных знаков, обозначение π становится общепринятым.

2037 десятичных знаков
1958 год — 10000 десятичных знаков
1961 год — 100000 десятичных знаков
1973 год — 10000000 десятичных знаков
1986 год — 29360000 десятичных знаков
1987 год — 134217000 десятичных знаков
1989 год — 1011196691 десятичный знак
1991 год — 2260000000 десятичных знаков
1994 год — 4044000000 десятичных знаков
1995 год — 4294967286 десятичных знаков
1997 год — 51539600000 десятичных знаков
1999 год — 206 158 430 000 десятичных знаков.

Суперкомпьютер в сентябре 1999 года работал 37 часов 21 минут 4 секунды, используя 865 Гбайт памяти для основной задачи, и 46 часов и 816 Гбайт для вспомогательной оптимизации вычислений.

дней в 2010 году) = 3,14

(Число дней в 2016 году) /(Число выходных дней в 2016 году) = 366 / 119 = 3,08

в Сиэтле

Двухметровая буква.
В Волгограде установили памятник числу пи

этим числом, что посвятил ему целый дворец  Кастель дель Монте,
в пропорциях которого можно вычислить π.

Сейчас волшебный дворец находится под охраной ЮНЕСКО.

по числу букв в каждом слове фразы:

Что я знаю о круге

3, 1 4 1 5

Но как уложить в память бесконечность? Любимый вопрос мнемонистов-профессионалов. Разработано множество уникальных теорий и приёмов освоения огромного количества информации. Многие из них опробованы на π.

Мировой рекорд, установленный в прошлом столетии в Германии –
40 000 знаков.

Российский рекорд значений числа π 1 декабря 2003 года в Челябинске установил Александр Беляев. За полтора часа с небольшими перерывами на школьной доске Александр написал 2500 цифр числа π.
До этого рекордным в России считалось перечислить 2000 знаков, что удалось сделать в 1999 году в Екатеринбурге. По словам Александра Беляева - руководителя центра развития образной памяти, такой эксперимент со своей памятью может провести любой из нас. Важно лишь знать специальные техники запоминания и периодически тренироваться.

Последний рекорд, достигнутый на суперкомпьютерах - это 500 млрд. знаков.

математического феномена, собирают все новые сведения о Пи и пытаются разгадать его тайну. Чтобы вступить в него, для начала надо вызубрить наизусть как можно большее количество чисел Пи после запятой. Пока рекорд принадлежит японцу Акира Харагучи, запомнившему 83 431 цифру.

так как в европейском формате дат этот день записывается как 22/7, а значение этой дроби является приближённым значением числа π.

Интересные факты о числе Пи

Международный праздник
«День числа Пи» отмечается 14 марта, которое в американском формате дат (месяц/день) записывается как 3.14,
что соответствует приближённому значению числа π.

Нить распрямляла и измеряла длину , приложив к линейке.

С помощью линейки находила длину диаметра.

С помощью калькулятора вычисляла
отношение длины окружности к диаметру С/d

Всё зафиксировала в таблице.

Фортепиано
Состав исполнителей Соло
Тип нот Для одного исполнителя

За основу мелодии я взяла 52 знака после запятой в числе "пи" (3,14). Каждая цифра соответствует определённой ноте. Но иногда, чтобы избежать больших скачков в мелодии ноты заменялись на аналогичные октавой выше. Вот такая получилась музыка…
 

повсюду. Не зря есть такая поговорка английского математика Моргана

« Число Пи лезет в дверь, в окно и через крышу»

Заключение