- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Средняя линия треугольника геометрия 8 класс
Содержание
- 1. Презентация Средняя линия треугольника геометрия 8 класс
- 2. повторить понятие подобия
- 3. Слайд 3
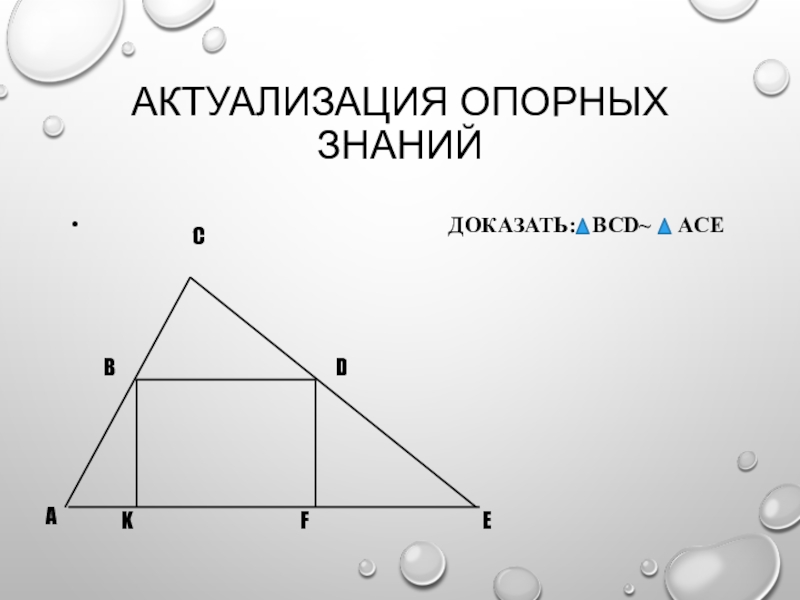
- 4. Актуализация опорных знаний
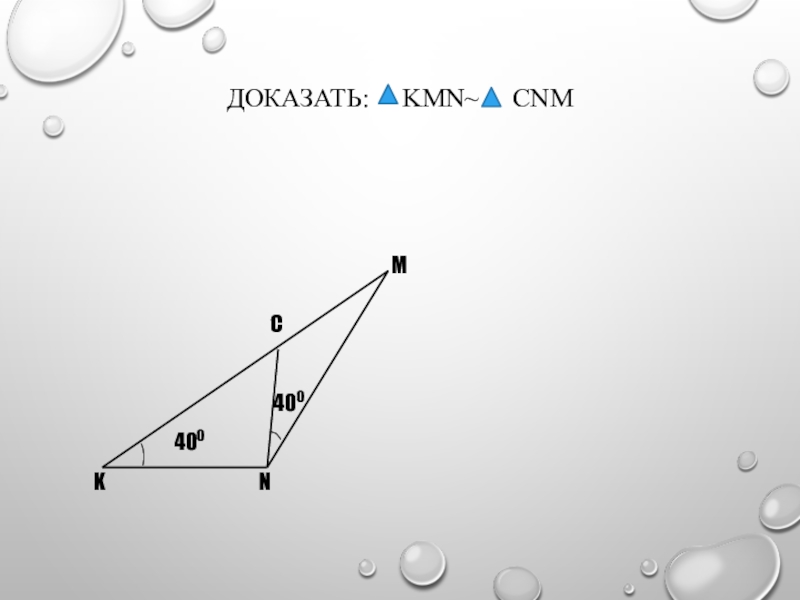
- 5. Доказать: KMN~ CNM
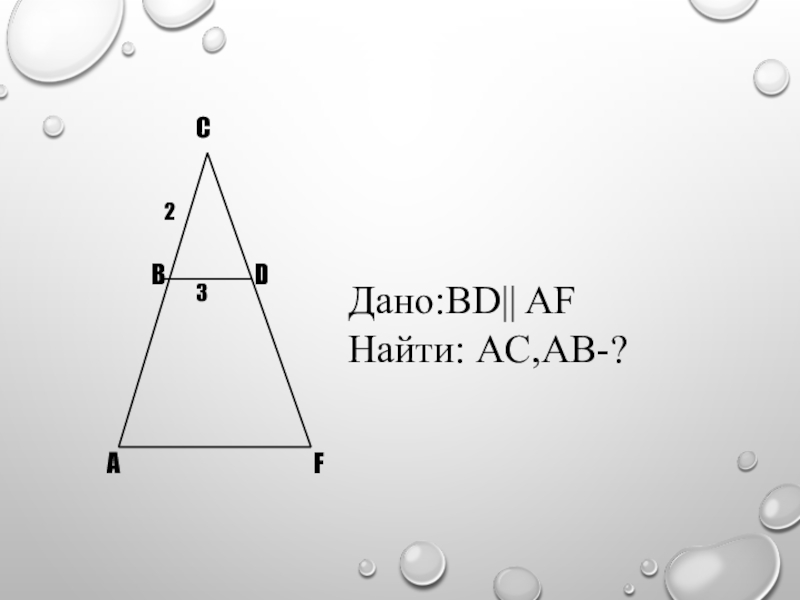
- 6. Дано:BD|| AFНайти: AC,AB-?
- 7. Верно ли? Два треугольника подобны, если их
- 8. 5.Назовите три признака подобия треугольников.6.Чему равно отношение периметров подобных треугольников?7. Чему равно отношение площадей подобных треугольников.
- 9. Средняя линия треугольника
- 10. Мои цели на урок:Узнать…..Познакомиться с …..Научиться применять ….
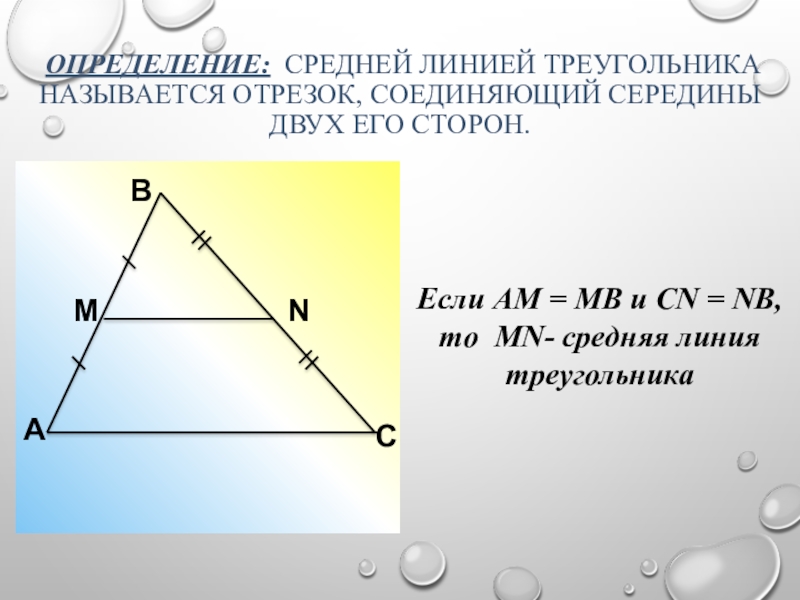
- 11. Определение: Средней линией треугольника называется отрезок,
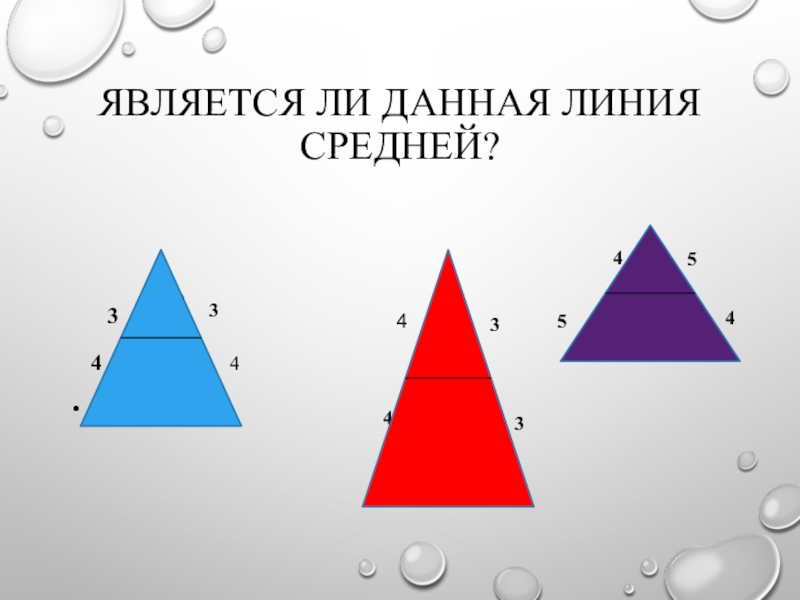
- 12. Является ли данная линия средней?
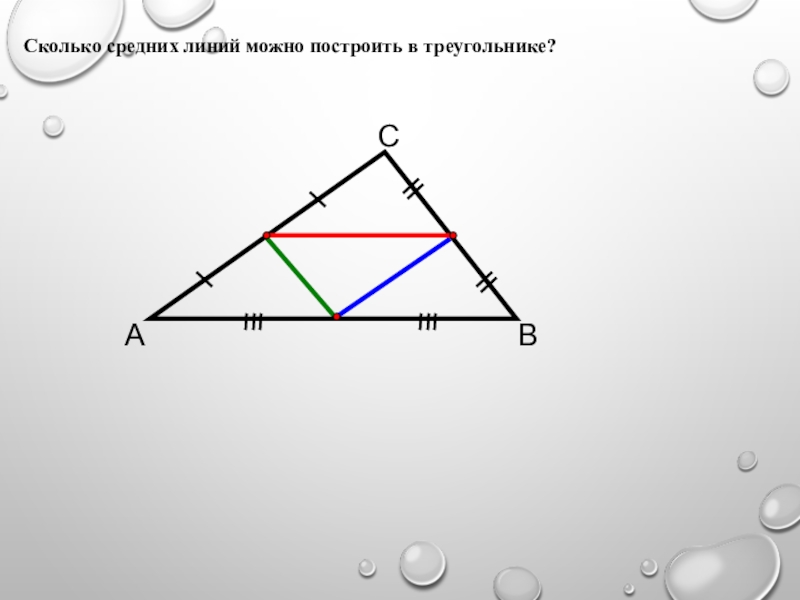
- 13. АСВСколько средних линий можно построить в треугольнике?
- 14. Теорема: Средняя линия треугольника параллельна одной из
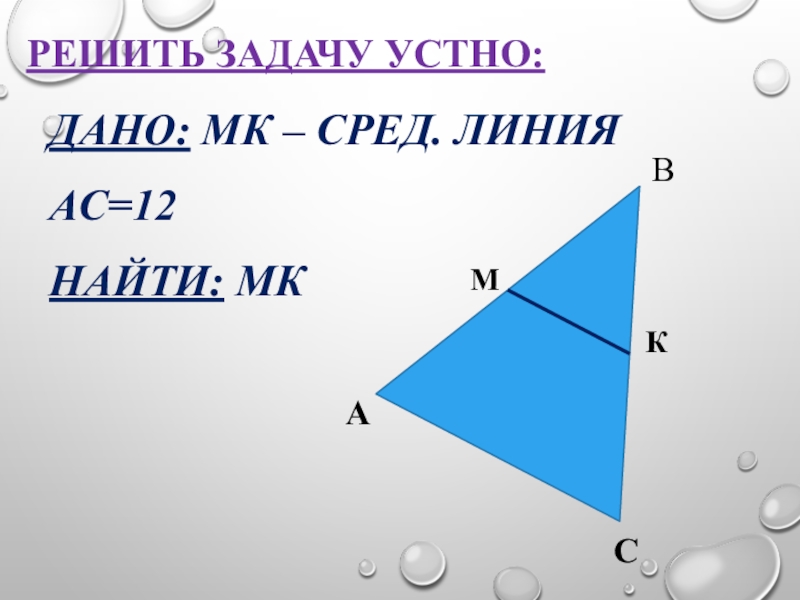
- 15. РЕШИТЬ ЗАДАЧУ УСТНО:Дано: MК – сред. линияАС=12Найти: MК АКМСВ
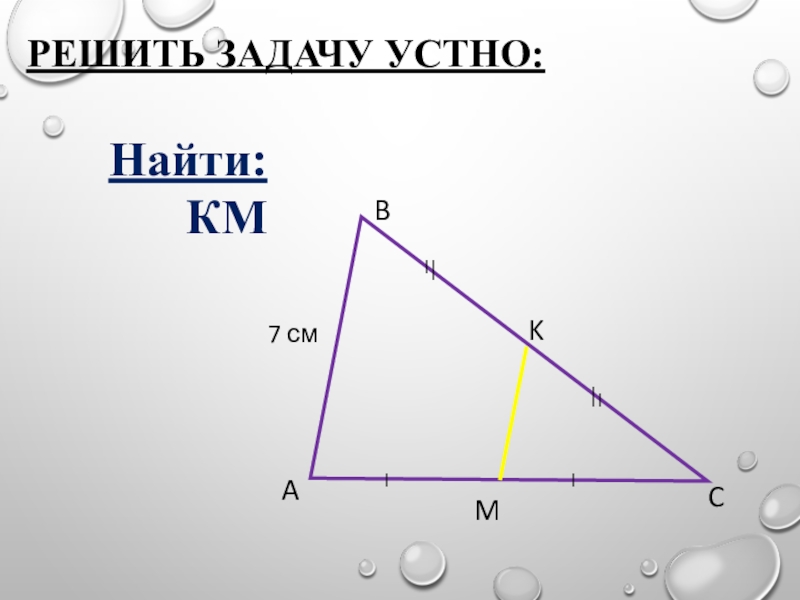
- 16. 7 смABCMKРЕШИТЬ ЗАДАЧУ УСТНО:Найти: КМ
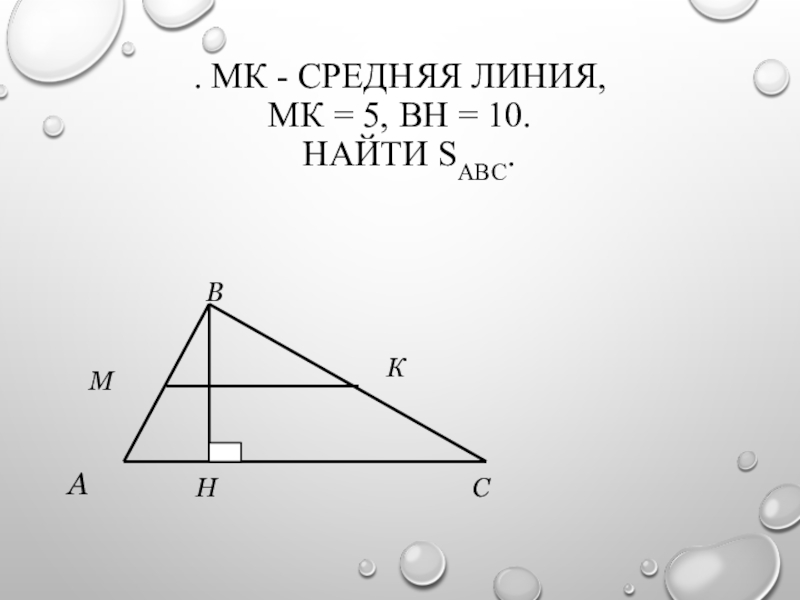
- 17. . МК - средняя линия, МК = 5, ВН = 10. Найти SАВС.
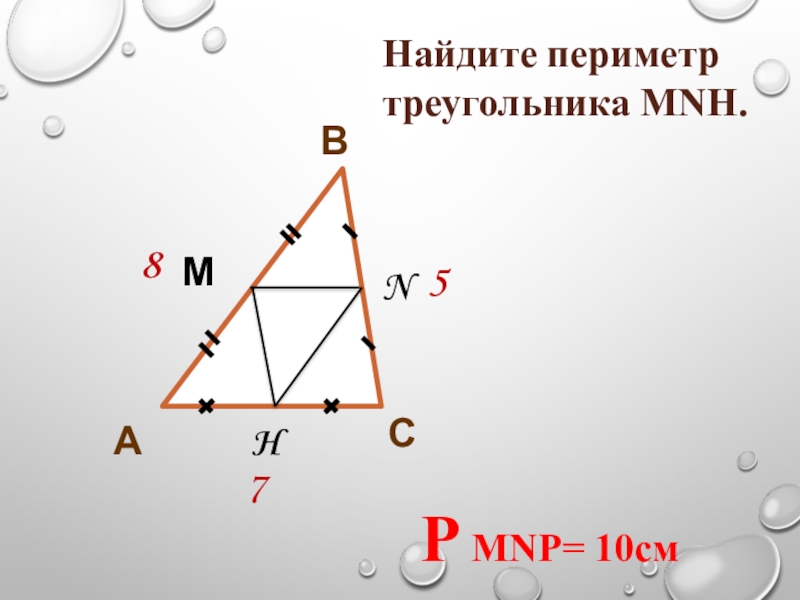
- 18. СВАМNH857Найдите периметр треугольника МNH.P MNP= 10см
- 19. Решить задачу
- 20. задача №1 стр 146. - постройте
- 21. Решить задачуВ треугольнике АВС медианы АА1, ВВ1,
- 22. Какие новые знания получены на уроке?Что называют
- 23. Домашнее заданиеОбязательный уровень: п.62 (стр.146), № , 556,570, 571ДополнительноСоставить задачи на готовых чертежах
Слайд 1МОУ «Школа №3» города Алушта
Средняя линия треугольника
8 класс
Учитель математики
Калиброва Лариса
Слайд 2 повторить понятие подобия треугольников и
Цели урока :
Слайд 7Верно ли?
Два треугольника подобны, если их углы
пропорциональны.
2. Два равносторонних треугольника иногда подобны.
3. Если три стороны одного треугольника
соответственно пропорциональны трем сторонам
другого треугольника, то такие треугольники подобны.
4. Если два угла одного треугольника равны 60 и 50, а два
угла другого треугольника равны 50 и 70, то такие
треугольники подобны
Слайд 85.Назовите три признака подобия треугольников.
6.Чему равно отношение периметров подобных треугольников?
7. Чему
Слайд 11 Определение: Средней линией треугольника называется отрезок, соединяющий середины двух его
А
В
С
М
N
Если АМ = МВ и СN = NВ, то МN- средняя линия треугольника
Слайд 14Теорема: Средняя линия треугольника параллельна одной из его сторон и равна
С
В
А
М
N
Дано: ΔАВС, МN – средняя линия.
Доказать: МN || АС, МN =½ АС
Доказательство:
ΔАВС ~ ΔВМN,
т.к. ВМ:ВА = ВN:ВС=1:2 и угол В – общий.
2. Угол ВМN равен углу ВАС, а они соответственные при прямых МN и АС и секущей АВ. Значит, МN || АС.
3. Т.к. ВМ:ВА =1:2, то и МN:АС=1:2.
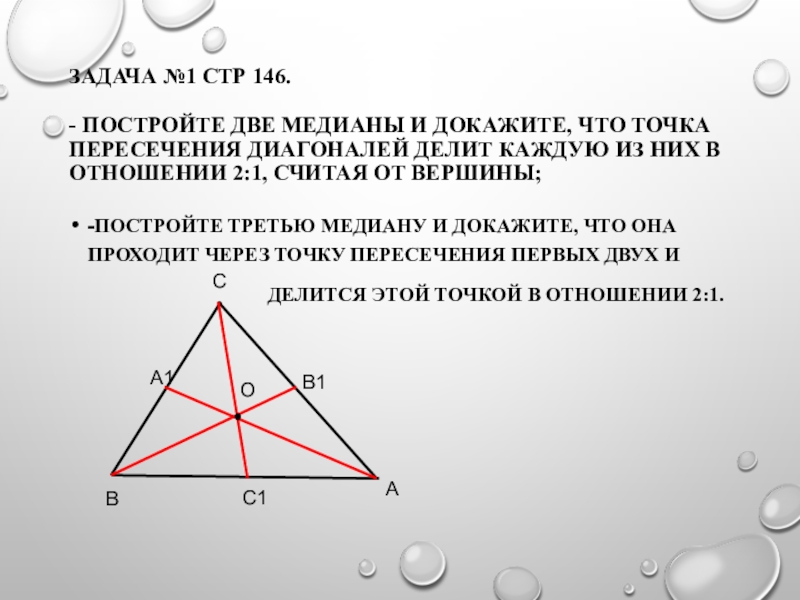
Слайд 20задача №1 стр 146. - постройте две медианы и докажите, что точка
-Постройте третью медиану и докажите, что она проходит через точку пересечения первых двух и
делится этой точкой в отношении 2:1.
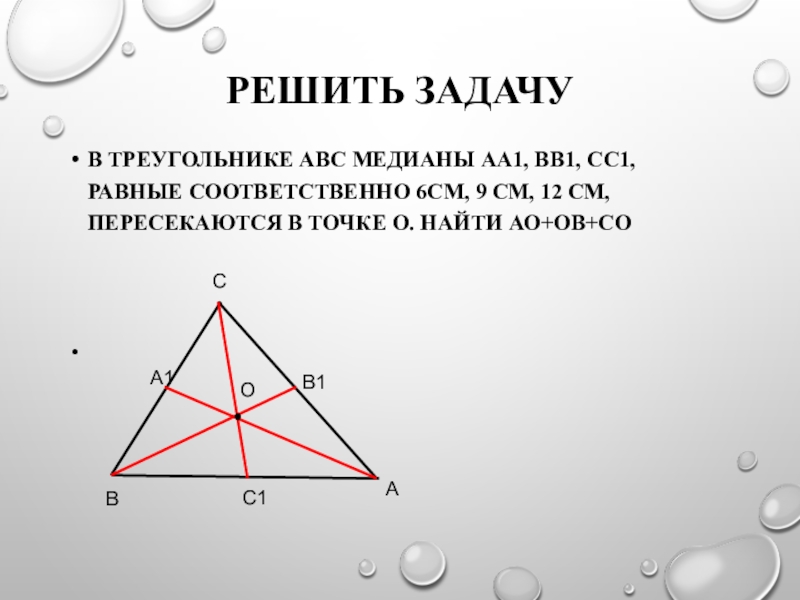
Слайд 21Решить задачу
В треугольнике АВС медианы АА1, ВВ1, СС1, равные соответственно 6см,
Слайд 22Какие новые знания получены на уроке?
Что называют средней линией треугольника?
Сформулируйте теорему
Вопросы, которые вы можете задать себе, одноклассникам, учителю.
Подведем итог