Урок геометрии в 8 классе
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Путешествие на острова многоугольников
Содержание
- 1. Презентация Путешествие на острова многоугольников
- 2. «Путешествие на острова четырехугольников»уок-грари
- 3. План урока:Повторение определения четырехугольника, многоугольника, выпуклого четырехугольника.Повторение
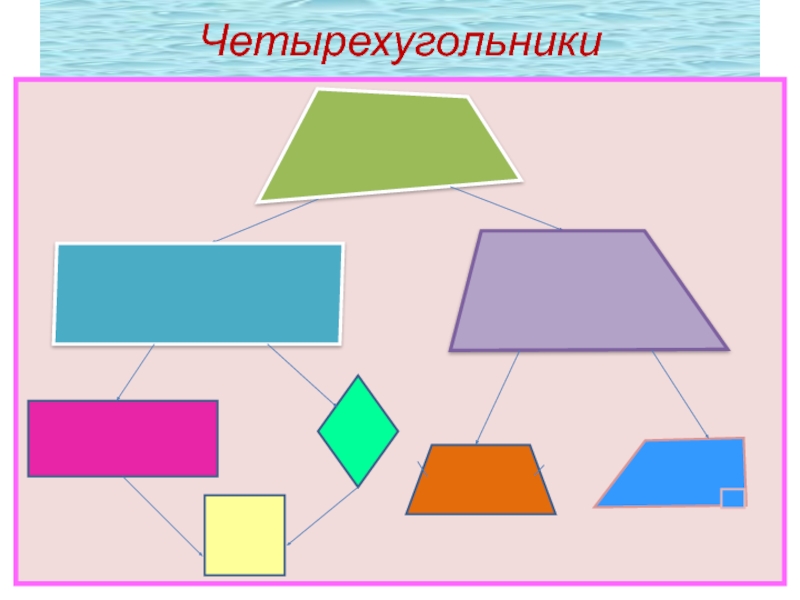
- 4. Четырехугольники
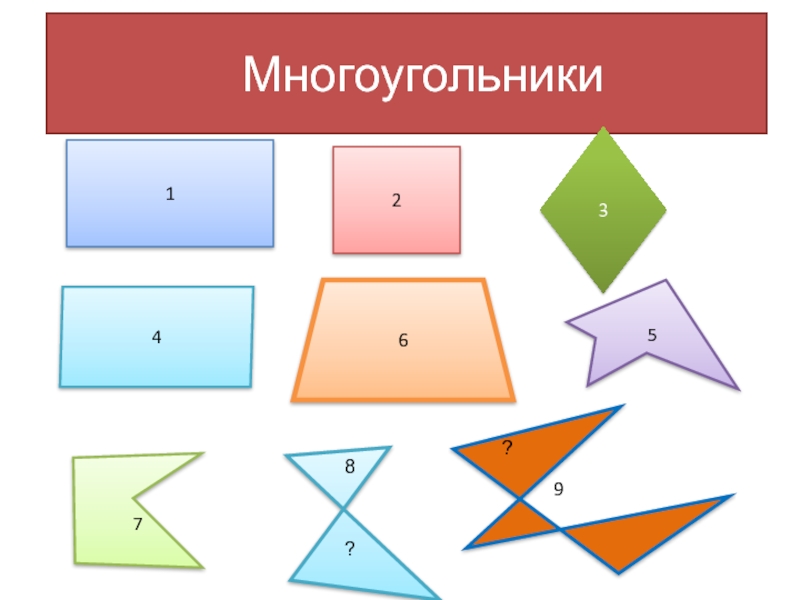
- 5. Многоугольники 12467539??8
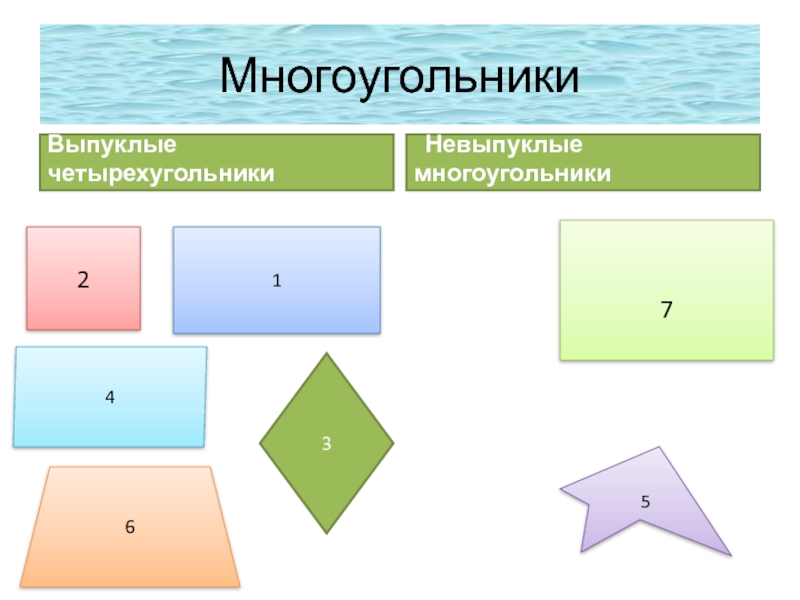
- 6. МногоугольникиВыпуклые четырехугольники2 Невыпуклые многоугольники7 14653
- 7. Из истории Термин «параллелограмм» греческого происхождения и,
- 8. СВОЙСТВА ПАРАЛЛЕЛОГРАММА В параллелограмме противоположные стороны
- 9. ПРИЗНАКИ ПАРАЛЛЕЛОГРАММА Если в четырехугольнике
- 10. У параллелограмма противоположные углы равныЗадача уровня
- 11. Задача уровня
- 12. Задача уровня В:
- 13. ПРЯМОУГОЛЬНИКМNSR
- 14. Особое свойство прямоугольника:
- 15. Задача уровня А: У прямоугольника
- 16. Из истории ромба
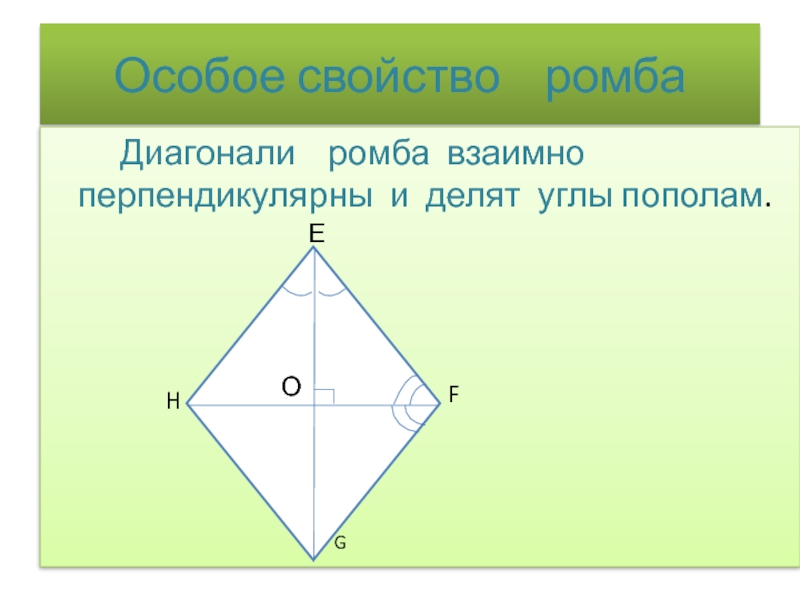
- 17. Особое свойство ромба
- 18. Решение задач1 Задача уровня А:Один из
- 19. Слайд 19
- 20. КВАДРАТКвадратом называется прямоугольник, у которого все стороны
- 21. Решение задач1.Задачи уровня А:У квадрата сторона равна
- 22. ABCDMN121)∠ 1 = 45° (диагональ квадрата является
- 23. Из истории о
- 24. 1 Задача уровня В. Основания
- 25. Решение задачи 1:ВDCA8126 – 4 = 2 смОтвет: 2 см64?2
- 26. ABCD2ххххПусть АВ = х, тогда х +
- 27. Тест №1(уровень А)1.Четырехугольник, у которого только 2
- 28. Т ЕСТ №2(УРОВЕНЬ В)1.Диагонали четырехугольника в
- 29. Тест №3 (уровень С)1.В равнобедренной трапеции один
- 30. Верно ли утверждение?Квадрат является параллелограммом.Параллелограмм
- 31. Диагонали параллелограмма являются биссектрисами его углов.Если у
- 32. Вопросы 1 команде1) Определение квадрата.2) Периметр
- 33. Вопросы 2
- 34. Заключение Прямоугольник, ромб, квадрат – частные виды параллелограмма, значит, обладают всеми свойствами параллелограмма.
- 35. Характерные свойстваПрямоугольник и квадратВсе углы
- 36. Площадь квадрата, прямоугольника и треугольникаS=а² (площадь квадрата
- 37. Слайд 37
- 38. Слайд 38
- 39. Урок окончен! До свидания!До встречи на острове Площадей
Слайд 1 «Путешествие на острова четырёхугольников»
Автор – Надгериева Джульетта Игнатовна, учитель
Слайд 3План урока:
Повторение определения четырехугольника, многоугольника, выпуклого четырехугольника.
Повторение свойств и признаков
Решение задач на повторение по уровням.
Тест (уровень А,В,С).
Командная игра «Быстро и правильно».
Итоги урока, выводы.
Домашнее задание.
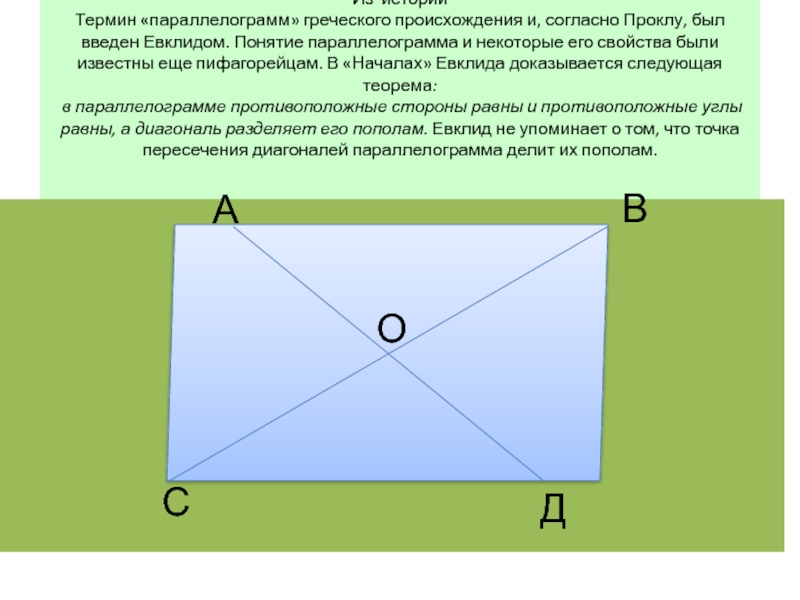
Слайд 7Из истории Термин «параллелограмм» греческого происхождения и, согласно Проклу, был введен Евклидом.
А
В
С
О
Д
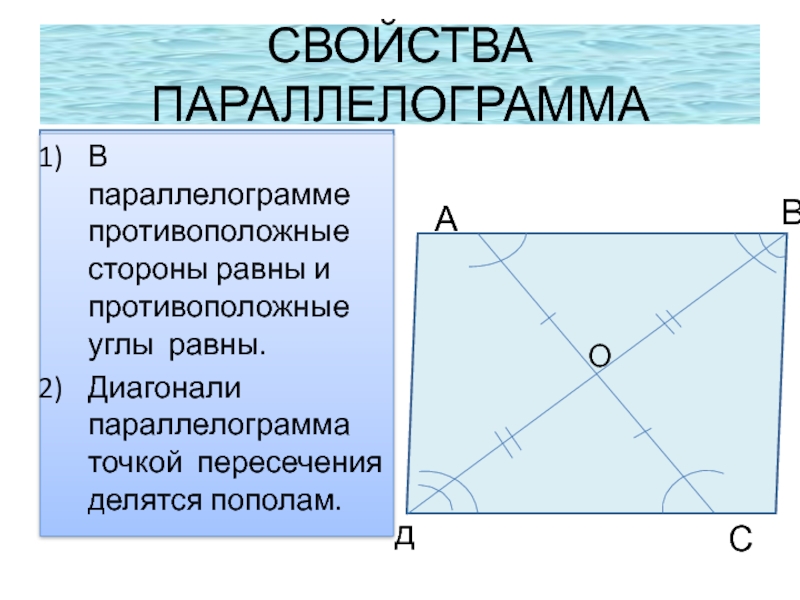
Слайд 8СВОЙСТВА ПАРАЛЛЕЛОГРАММА
В параллелограмме противоположные стороны равны и противоположные углы
Диагонали параллелограмма точкой пересечения делятся пополам.
А
В
С
О
д
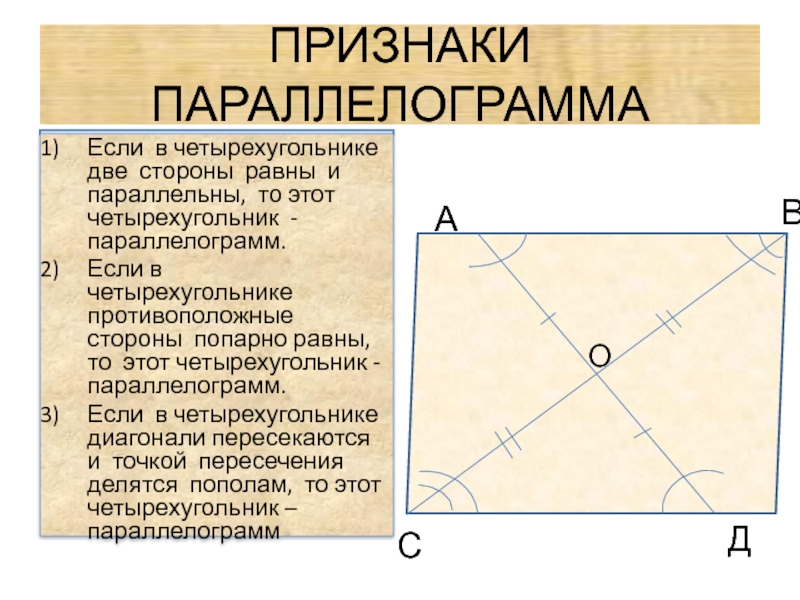
Слайд 9ПРИЗНАКИ ПАРАЛЛЕЛОГРАММА
Если в четырехугольнике две стороны равны и
Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник - параллелограмм.
Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник – параллелограмм
А
В
С
Д
О
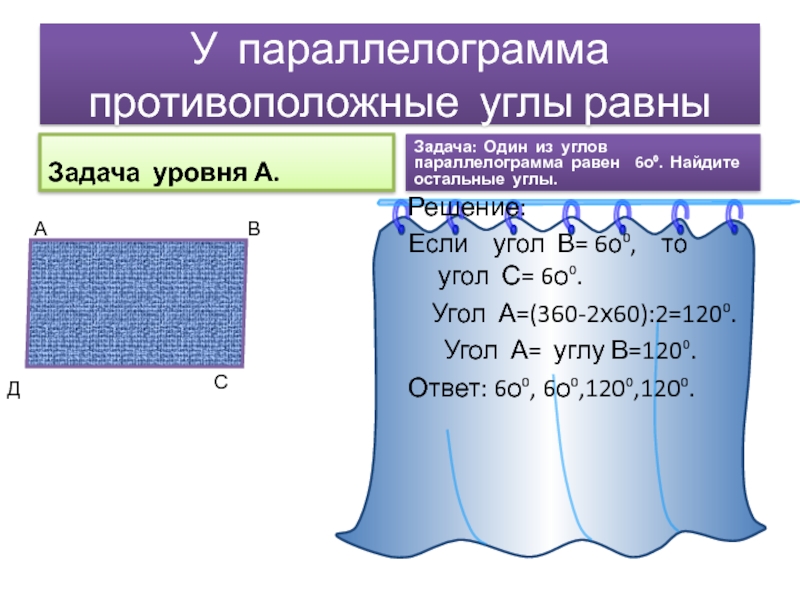
Слайд 10У параллелограмма противоположные углы равны
Задача уровня А.
Задача: Один из углов
Решение:
Если угол В= 6о⁰, то угол С= 6о⁰.
Угол А=(360-2х60):2=120⁰.
Угол А= углу В=120⁰.
Ответ: 6о⁰, 6о⁰,120⁰,120⁰.
А
В
С
Д
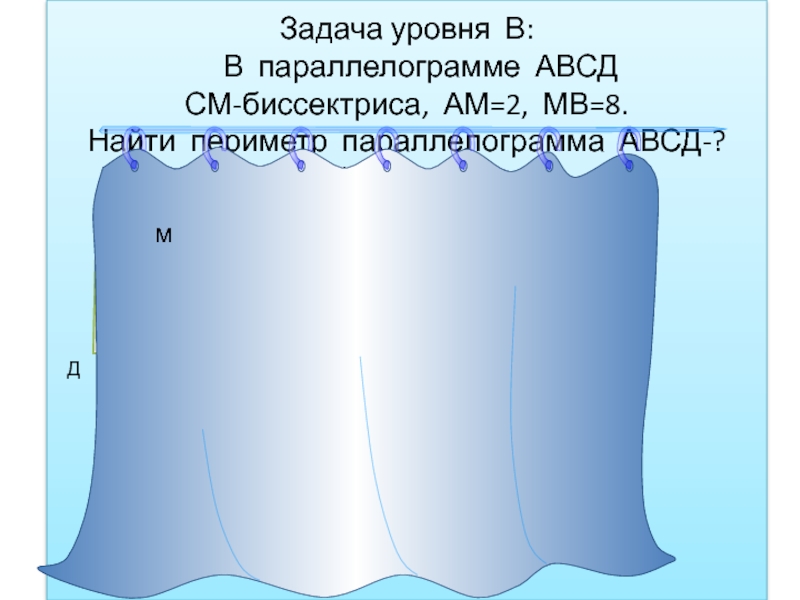
Слайд 11 Задача уровня В: В параллелограмме АВСД СМ-биссектриса, АМ=2, МВ=8. Найти периметр параллелограмма
А
В
С
Д
1
2
3
м
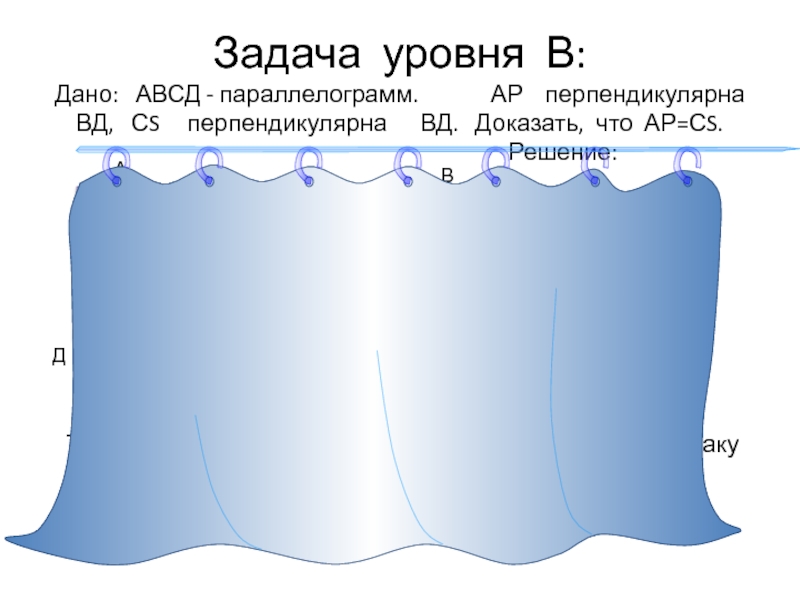
Слайд 12 Задача уровня В: Дано: АВСД - параллелограмм.
А
В
С
Д
Р
S
1
2
Слайд 14
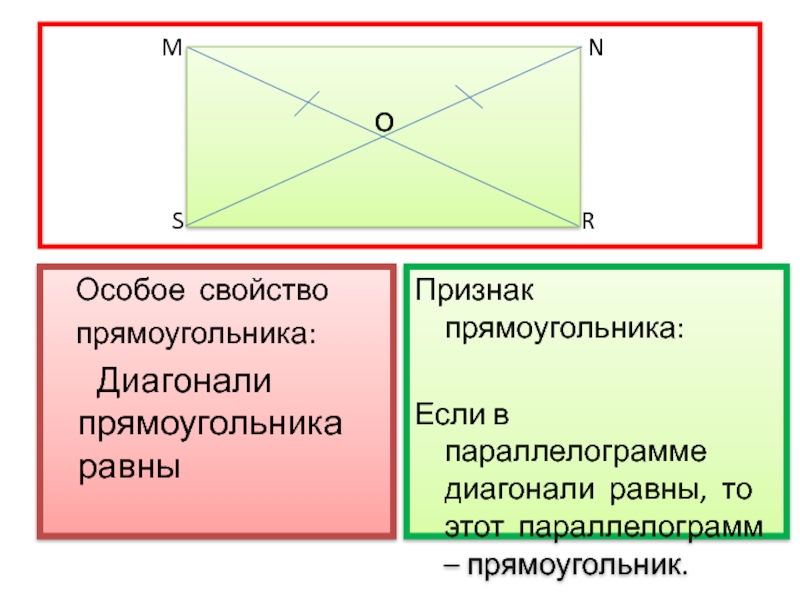
Особое свойство
прямоугольника:
Диагонали
Признак прямоугольника:
Если в параллелограмме диагонали равны, то этот параллелограмм – прямоугольник.
M
R
N
S
о
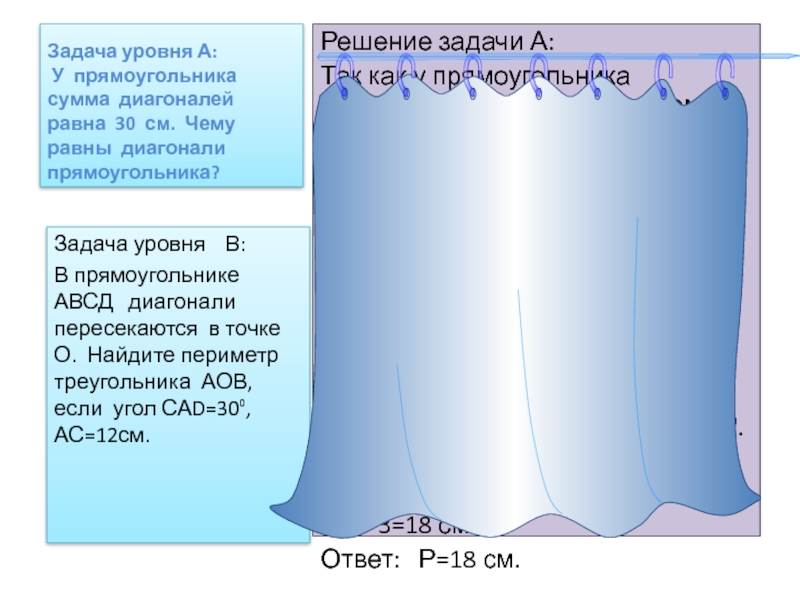
Слайд 15Задача уровня А: У прямоугольника сумма диагоналей равна 30
Решение задачи А:
Так как у прямоугольника диагонали равны, то имеем: 30:2=15(см)
Ответ: по 15 см.
Решение задачи В:
Так как АС=12см,
то АО=6см.
Так как ВД=АС, а диагонали точкой пересечения делятся пополам, то АО=ВО=6см. <ОАВ=90⁰-30⁰=60⁰,
<ОАВ=<ОВА, <ВОА=180⁰-60⁰*2=60⁰.
Треугольник АОВ- равносторонний и
Р=6*3=18 см.
Ответ: Р=18 см.
Задача уровня В:
В прямоугольнике АВСД диагонали пересекаются в точке О. Найдите периметр треугольника АОВ, если угол САD=30⁰, АС=12см.
В
С
А
Д
О
30
60
Слайд 16 Из истории ромба Слово « ромб» тоже греческого
E
F
G
H
РОМБ
Слайд 18Решение задач
1 Задача уровня А:
Один из углов ромба равен 30⁰.Найдите
2 Задача уровня А:
Найдите углы, которые образуют диагонали ромба с его сторонами, если один из углов ромба равен
60⁰.
3 Задача уровня В:
Найдите длину меньшей диагонали ромба, если периметр ромба равен 24 см, а больший угол=120⁰.
Слайд 19
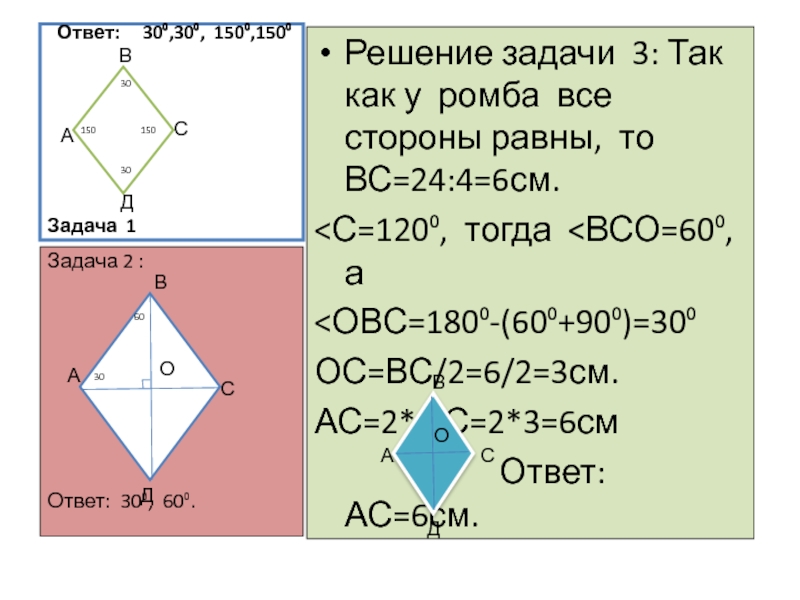
Решение задачи 3: Так как у ромба все стороны равны, то ВС=24:4=6см.
<С=120⁰, тогда <ВСО=60⁰, а
<ОВС=180⁰-(60⁰+90⁰)=30⁰
ОС=ВС/2=6/2=3см.
АС=2*ОС=2*3=6см
Ответ: АС=6см.
Задача 2 :
Ответ: 30⁰, 60⁰.
А
В
С
Д
30
30
150
150
А
В
С
Д
О
30
60
А
В
С
Д
О
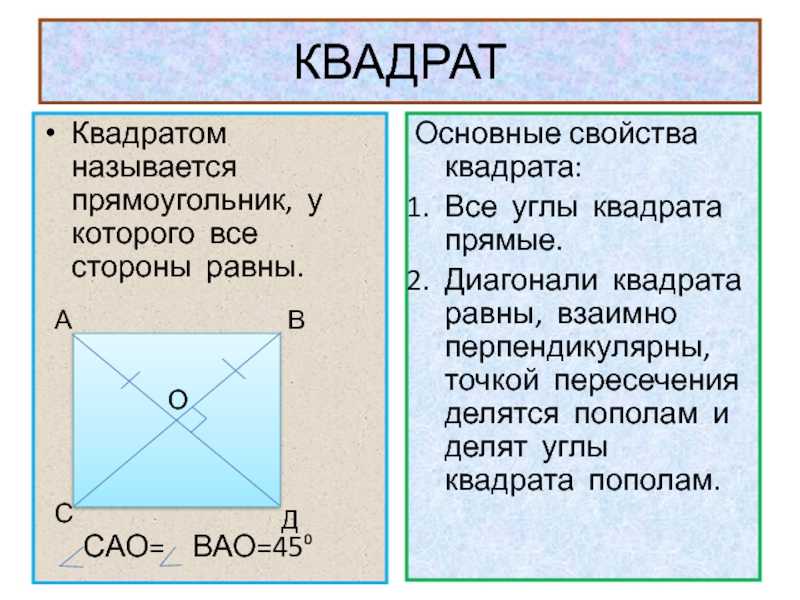
Слайд 20КВАДРАТ
Квадратом называется прямоугольник, у которого все стороны равны.
САО=
Основные свойства квадрата:
Все углы квадрата прямые.
Диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам и делят углы квадрата пополам.
А
В
С
Д
О
Слайд 21Решение задач
1.Задачи уровня А:
У квадрата сторона равна 8 см. Чему равен
2. Чему равна градусная мера угла, образованного одной из сторон квадрата и его диагональю?
Задача уровня В:
Дано: ABCD – квадрат, АС = 15см, МN ⊥ AC,
МN ∩ BC = M, МN ∩ DC = N
Найти: MN
Слайд 22
A
B
C
D
M
N
1
2
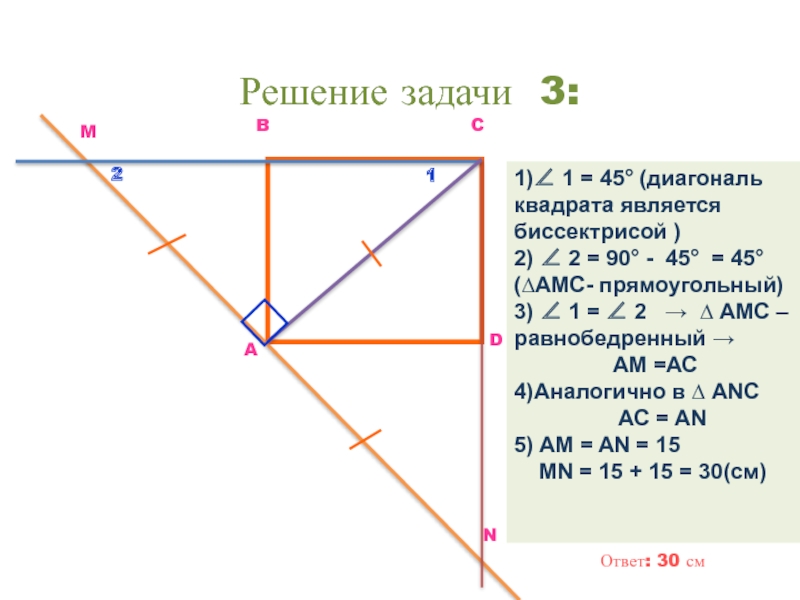
1)∠ 1 = 45° (диагональ квадрата является биссектрисой )
2) ∠ 2
3) ∠ 1 = ∠ 2 → ∆ АМС – равнобедренный →
АМ =АС
4)Аналогично в ∆ АNС
AC = AN
5) AM = AN = 15
MN = 15 + 15 = 30(cм)
Решение задачи 3:
Ответ: 30 см
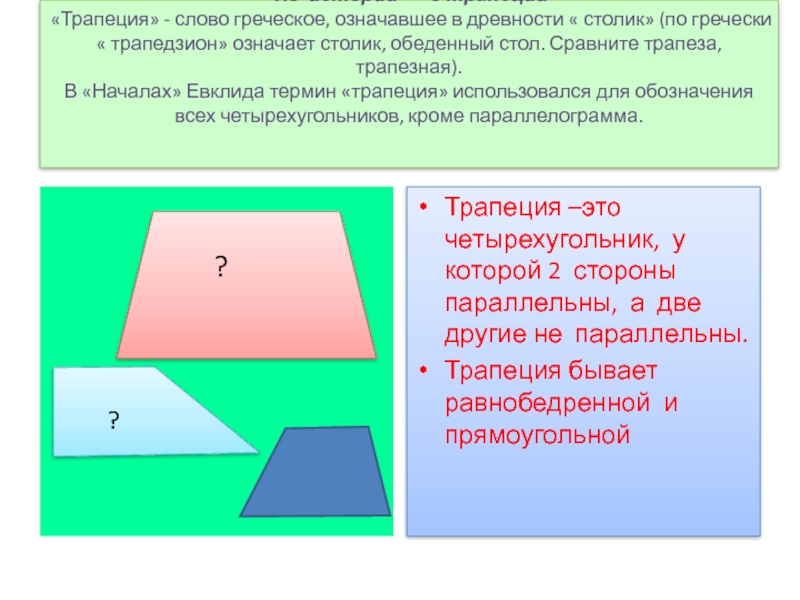
Слайд 23 Из истории о трапеции «Трапеция» - слово греческое,
Трапеция –это четырехугольник, у которой 2 стороны параллельны, а две другие не параллельны.
Трапеция бывает равнобедренной и прямоугольной
?
?
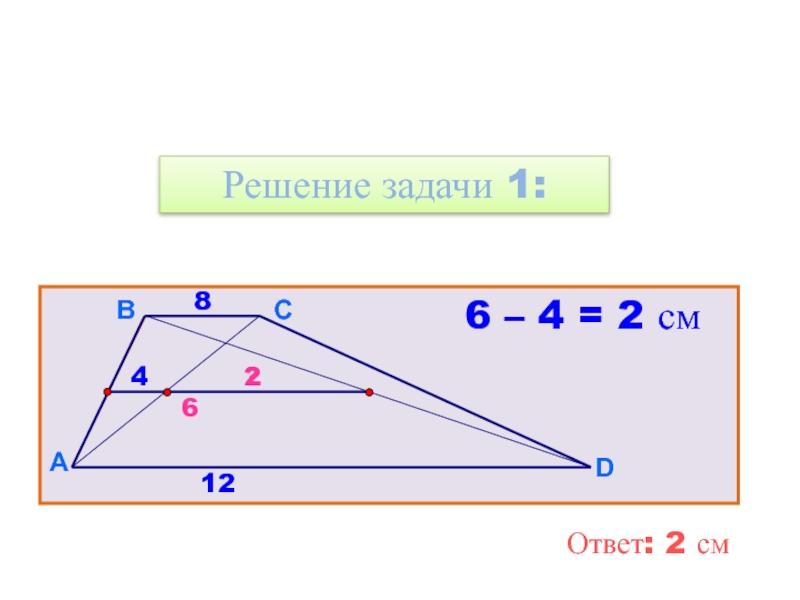
Слайд 241 Задача уровня В. Основания трапеции равны 8 и
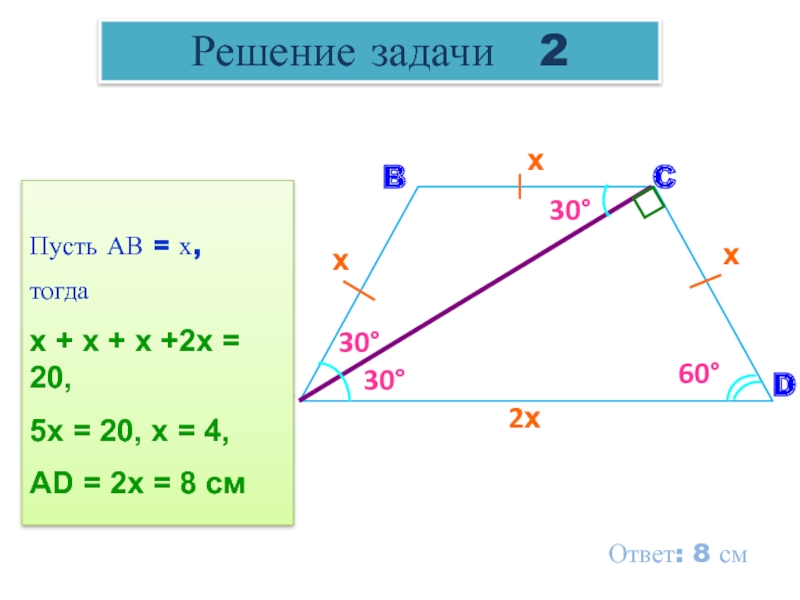
2 Задача уровня В. Дано: ABCD – равнобедренная трапеция, PABCD= 20см,
диагональ АС – биссектриса угла А, AC ⊥ CD, ∠ D = 60°
Найти AD
Слайд 26
A
B
C
D
2х
х
х
х
Пусть АВ = х,
тогда
х + х + х +2х
5х = 20, х = 4,
AD = 2х = 8 см
30°
30°
30°
Ответ: 8 см
Решение задачи 2
Слайд 27Тест №1(уровень А)
1.Четырехугольник, у которого только 2 стороны параллельны
Ромб
Трапеция
Квадрат
Прямоугольник
2.Трапеция, у которой
Равнобедренной
Остроугольной
Тупоугольной
Прямоугольной
3.Любой ромб является
Квадратом
Прямоугольником
Параллелограммом
Трапецией
4. Если в параллелограмме все стороны равны и диагонали перпендикулярны, то этот параллелограмм
Ромб
Квадрат
Прямоугольник
Нет правильного ответа
5.Любой прямоугольник является
Ромбом
Квадратом
Параллелограммом
Нет правильного ответа
Слайд 28Т ЕСТ №2(УРОВЕНЬ В)
1.Диагонали четырехугольника в точке пересечения делятся пополам.
2см
8см
4см
6см
2.Сумма двух углов параллелограмма равна 100⁰. Найдите углы параллелограмма
40,140
80,100
50,130
40,60
3.Сумма углов выпуклого четырехугольника равна
180
360
540
160
4.Квадрат –это…
Параллелограмм с равными углами
Параллелограмм с равными сторонами
Прямоугольник, у которого все стороны равны
Нет правильного ответа.
5.У этого четырехугольника диагонали равны?
Трапеция
Прямоугольник
Ромб
параллелограмм
Слайд 29Тест №3 (уровень С)
1.В равнобедренной трапеции один из углов равен 110⁰.Найдите
55,55,125,125
180,70,180,70
70,110,70,110
Нет верного ответа
2.Какое из утверждений неверное?
У прямоугольника углы прямые
У ромба все стороны равны
У квадрата диагонали взаимно перпендикулярны
У трапеции стороны попарно параллельны
3.Найдите периметр ромба, если один из его углов равен 60⁰, а меньшая диагональ равна 12 см.
48см
36см
24см
72см
4.Какое утверждение неверно
Квадрат - одновременно параллелограмм и прямоугольник
Угол между стороной и диагональю квадрата равен 45⁰.
Диагонали квадрата взаимно перпендикулярны
Существует квадрат, который не является ромбом.
Слайд 30 Верно ли утверждение?
Квадрат является параллелограммом.
Параллелограмм является квадратом.
Ромб является квадратом.
Квадрат
Прямоугольник является квадратом.
Прямоугольник является параллелограммом.
Параллелограмм с прямым углом – это прямоугольник.
Диагонали ромба равны.
Если диагонали четырехугольника перпендикулярны, то он является ромбом.
Слайд 31Диагонали параллелограмма являются биссектрисами его углов.
Если у четырехугольника противолежащие стороны равны,
Если диагонали четырехугольника равны, то это прямоугольник.
Диагонали прямоугольника являются биссектрисами его углов.
Диагонали ромба являются биссектрисами его углов.
Если в параллелограмме две смежные стороны равны и перпендикулярны, то он является квадратом.
Слайд 32 Вопросы 1 команде
1) Определение квадрата.
2) Периметр прямоугольника 20, одна сторона
(6)
3) Ромб – это параллелограмм?
(да)
4) Средняя линия треугольника равна основанию.
(нет)
5) В параллелограмме диагонали равны.
(нет)
6) Сумма углов при одной стороне параллелограмма 1800.
(да)
7) Периметр квадрата 40,а сторона?
(10)
8) Трапеция – параллелограмм.
(нет)
9) Диагонали ромба – биссектрисы его углов.
(да)
10) Диагонали квадрата равны.
(да)
11) Ромб – это квадрат.
(нет)
12) Диагонали параллелограмма пересекаются в одной точке.
(да)
13) Средняя линия трапеции равна половине основания.
(нет)
14) Сторона квадрата 4, периметр ?
(16)
15) У равнобокой трапеции боковые стороны перпендикулярны.
(нет)
Слайд 33 Вопросы 2 команде
Сумма углов при одной
(нет)
2) Ромб – это квадрат.
(нет)
3) Периметр параллелограмма 22 см, одна сторона 4 см, другая?
(7)
4) Диагонали ромба перпендикулярны.
(да)
5) Стороны параллелограмма равны.
(нет)
6) Острый угол параллелограмма 300, тупой 1200.
(нет)
7) Параллелограмм – это пятиугольник.
(нет)
8) У трапеции только две стороны параллельны
(да)
11) Трапеция – это ромб.
(нет)
12) Средняя линия треугольника параллельна третьей стороне.
(да)
13) Средняя линия треугольника 5 см. Чему равно основание?
(10)
14) Периметр – это произведение сторон.
(нет)
15) У квадрата все стороны равны.
(да)
Слайд 34Заключение
Прямоугольник, ромб, квадрат – частные виды параллелограмма, значит,
Слайд 35
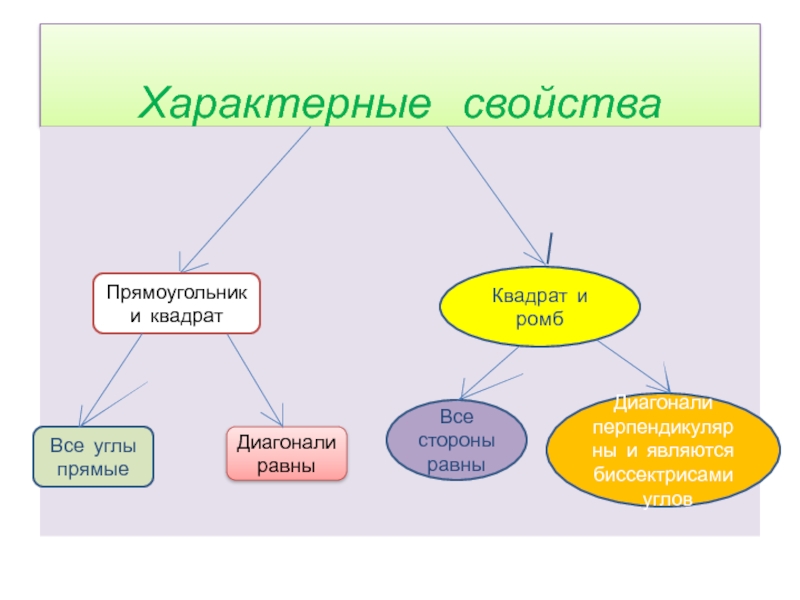
Характерные свойства
Прямоугольник и квадрат
Все углы прямые
Диагонали равны
Квадрат и ромб
Все стороны
Диагонали перпендикулярны и являются биссектрисами
углов
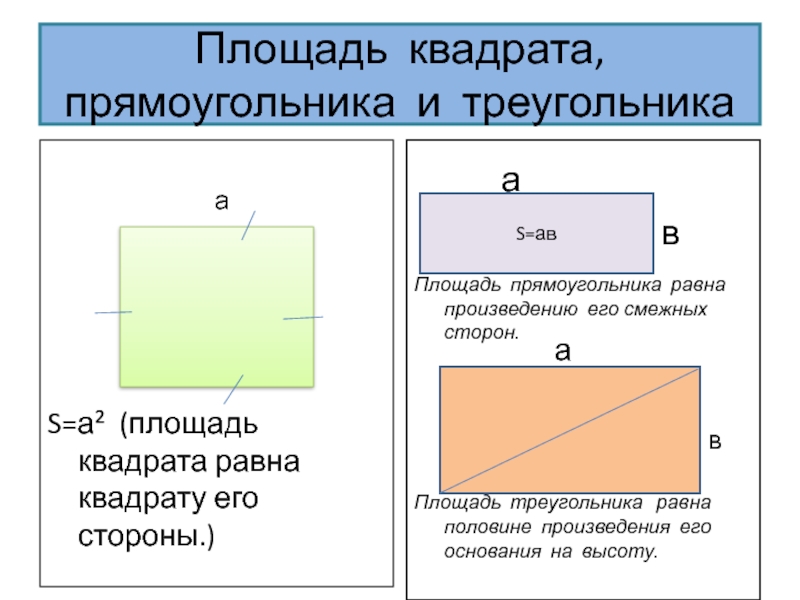
Слайд 36Площадь квадрата, прямоугольника и треугольника
S=а² (площадь квадрата равна квадрату его стороны.)
Площадь
Площадь треугольника равна половине произведения его основания на высоту.
а
S=ав
а
в
а
в