- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад проекта на тему: Окружность
Содержание
- 1. Презентация проекта на тему: Окружность
- 2. Актуальность Сегодня перед каждым девятиклассником
- 3. Цель Создание ресурса для повторения и отработки темы «Окружность» в виде презентации.
- 4. Задачи 1) Дать определение основных понятий. 2)
- 5. Этапы
- 6. II. Основной этап 1) Подбор теоретического материала 2) Составление набора задач 3) Оформление презентации
- 7. III.Проведение занятия - погружение.
- 8. Окружность, касательная и хорда.
- 9. Раздел 1 Основные понятия
- 10. Окружность Окружность – замкнутая плоская кривая, все
- 11. Радиус окружностиОтрезок, соединяющий центр окружности с любой из точек окружности называется радиусом.
- 12. ДиаметрДиаметр-это отрезок, соединяющий две точки на окружности
- 13. Касательная Прямая, которая имеет с окружностью ровно
- 14. Секущая Секущая — это прямая, пересекающая окружность
- 15. Хорда• Хорда — это отрезок, соединяющий две
- 16. Раздел 2
- 17. Группа 1
- 18. Центральный уголУгол, вершина которого лежит в центре
- 19. Вписанный угол • Угол вершина которого лежит
- 20. Если две хорды пересекаются, то произведение отрезков
- 21. Если сумма противоположных углов четырёхугольника равна 180 градусов, то около него можно описать окружность.
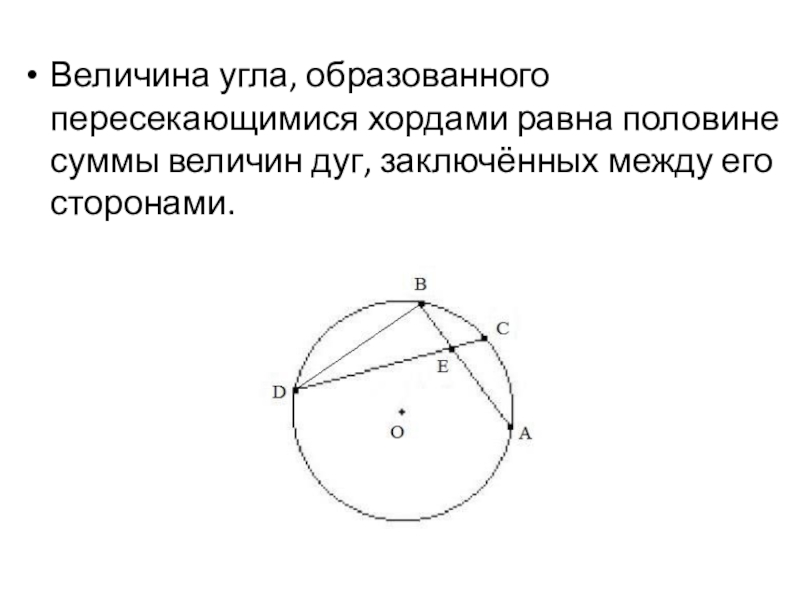
- 22. Величина угла, образованного пересекающимися хордами равна половине суммы величин дуг, заключённых между его сторонами.
- 23. Группа 2
- 24. Касательная к окружности перпендикулярна к радиусу, проведённому
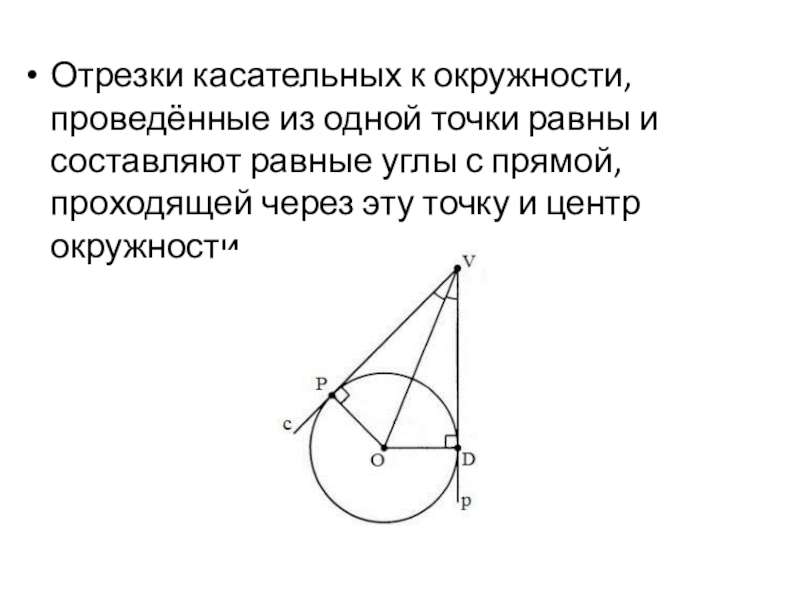
- 25. Отрезки касательных к окружности, проведённые из одной
- 26. Если прямая проходит через конец радиуса, лежащего
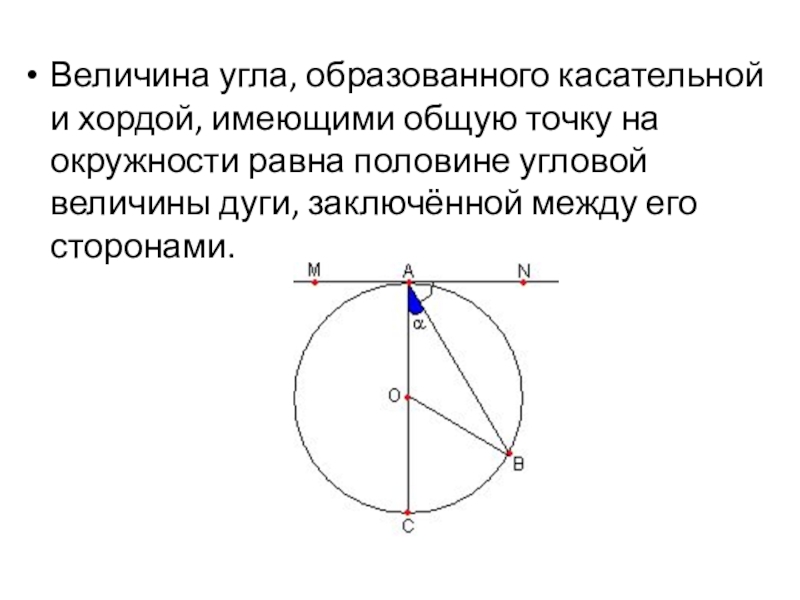
- 27. Величина угла, образованного касательной и хордой, имеющими
- 28. Если из точки к окружности проведены касательная
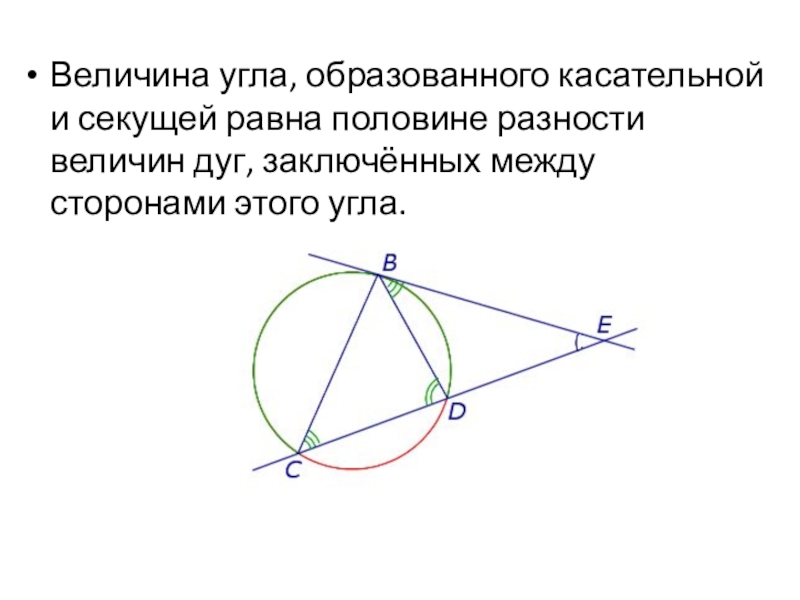
- 29. Величина угла, образованного касательной и секущей равна
- 30. Если через точку, лежащую вне окружности проведены
- 31. Величина угла, образованного двумя касательными к окружности
- 32. Раздел 3 Разбор задач
- 33. Задача 1Найдите хорду, на которую опирается угол
- 34. Задачи для закрепления
- 35. Задача 1Найдите градусную меру угла АОС если,
- 36. Задача 2Найдите градусную меру угла АВС если,
- 37. Задача 3 Найдите градусную меру дуги, на
- 38. Задача 2Прямая касается окружности в точке K.
- 39. Задачи для закрепления
- 40. Задача 1Прямая касается окружности в точке K.
- 41. Задача 2Прямая касается окружности в точке K.
- 42. Задача 3• Прямая касается окружности в точке
- 43. Задача 3 Через концы А , В
- 44. Задачи на закрепление
- 45. Задача 1Через концы А , В дуги
- 46. Задача 2 Через концы А , В
- 47. Задача 3Через концы А , В дуги
- 48. Задача 4 Найдите угол АСО, если его
- 49. Задачи для закрепления
- 50. Задача 1Найдите угол АСО, если его сторона
- 51. Задача 2 Найдите угол АСО, если его
- 52. Задача 3 Угол АСО равен 71 градус,
- 53. Задача 5 В окружности с центром в
- 54. Задачи для закрепления
- 55. Задача 1 В окружности с центром в
- 56. Задача 2В окружности с центром в точке
- 57. Задача 3В окружности с центром в точке
- 58. Задача 6В угол величиной 70° вписана окружность,
- 59. Задачи для закрепления
- 60. Задача 1В угол величиной 80° вписана окружность,
- 61. Задача 2 В угол вписана окружность, которая
- 62. Задача 3В угол величиной 35° вписана окружность,
- 63. Задача 7 Касательные в точках A и
- 64. Задачи для закрепления
- 65. Задача 1Касательные в точках A и B
- 66. Задача 2Касательные в точках A и B
- 67. Задача 3Касательные в точках A и B
- 68. Задача 8 В окружности с центром
- 69. Задачи для закрепления
- 70. Задача 1В окружности с центром O, AC
- 71. Задача 2 В окружности с центром О
- 72. Задача 3В окружности с центром в точке
- 73. Задача 9В треугольнике ABC угол C равен
- 74. Задачи на закрепление
- 75. Задача 1 В треугольнике ABC угол C
- 76. Справочные материалы.1.) Геометрия. 7-9 классы: учеб. для
Слайд 1Проект
Выполнила: ученица 9 «А» класса МАОУ «Школа № 3»
Окулова Алина
Руководитель: учитель математики
Мажарова Ирина Александровна
Слайд 2Актуальность
Сегодня перед каждым девятиклассником стоит серьёзная задача –
Слайд 4Задачи
1) Дать определение основных понятий.
2) Сформулировать теоремы, относящиеся
3) Составить набор необходимых задач-прототипов по теме «Окружность».
4) Провести занятие-погружение по теме «Окружность» для девятиклассников
Слайд 6II. Основной этап
1) Подбор теоретического материала
2) Составление
3) Оформление презентации
Слайд 10Окружность
Окружность – замкнутая плоская кривая, все точки которой одинаково удалены
О
Слайд 11Радиус окружности
Отрезок, соединяющий центр окружности с любой из точек окружности называется
Слайд 12Диаметр
Диаметр-это отрезок, соединяющий две точки на окружности и проходящая через центр
Диаметр равен двум радиусам.
d=2R
Слайд 13Касательная
Прямая, которая имеет с окружностью ровно одну общую точку, называется
Основные свойства:
• Касательная перпендикулярна радиусу окружности, проведенному к точке касания.
• Через любую точку вне окружности можно провести ровно две касательные к окружности.
• Отрезки касательных, проведенных к окружности из одной точки, от общей точки до точек касания равны друг другу.
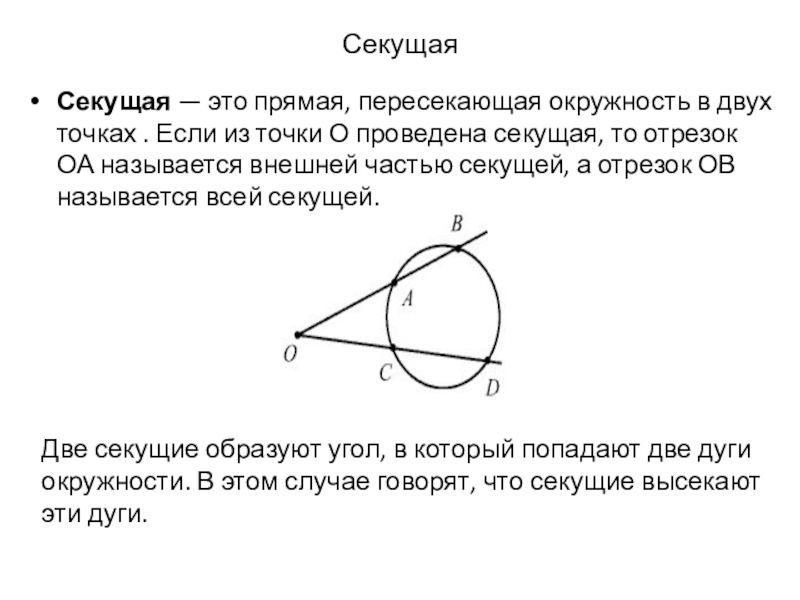
Слайд 14Секущая
Секущая — это прямая, пересекающая окружность в двух точках .
Две секущие образуют угол, в который попадают две дуги окружности. В этом случае говорят, что секущие высекают эти дуги.
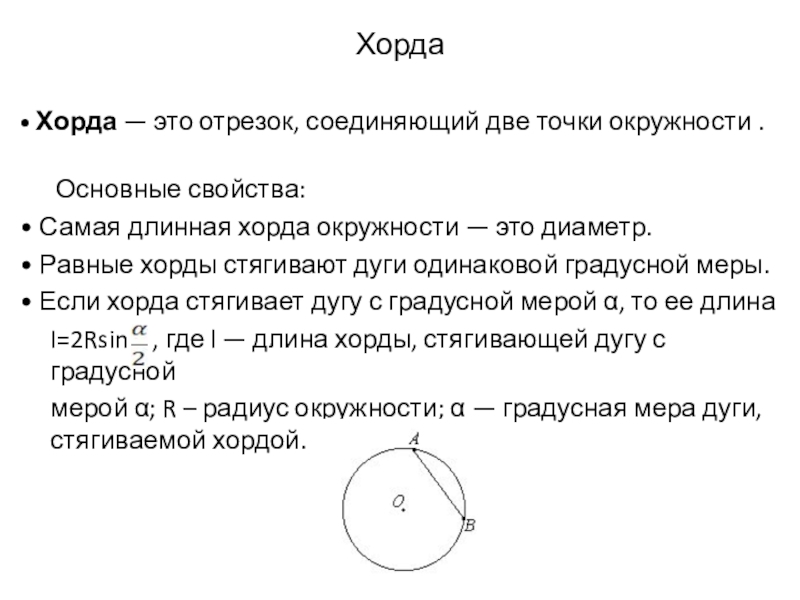
Слайд 15Хорда
• Хорда — это отрезок, соединяющий две точки окружности .
• Самая длинная хорда окружности — это диаметр.
• Равные хорды стягивают дуги одинаковой градусной меры.
• Если хорда стягивает дугу с градусной мерой α, то ее длина
I=2Rsin , где l — длина хорды, стягивающей дугу с градусной
мерой α; R – радиус окружности; α — градусная мера дуги, стягиваемой хордой.
Слайд 16Раздел 2
Все теоремы разделены на две группы. К первой группе относятся теоремы о вписанном угле и те теоремы, в доказательстве которых используется теорема о вписанном угле, а также теорема о центральном угле. Ко второй группе относятся теоремы, выражающие свойства касательных и секущих.
Слайд 18Центральный угол
Угол, вершина которого лежит в центре окружности, называется центральным.
Величина центрального
А
О
С
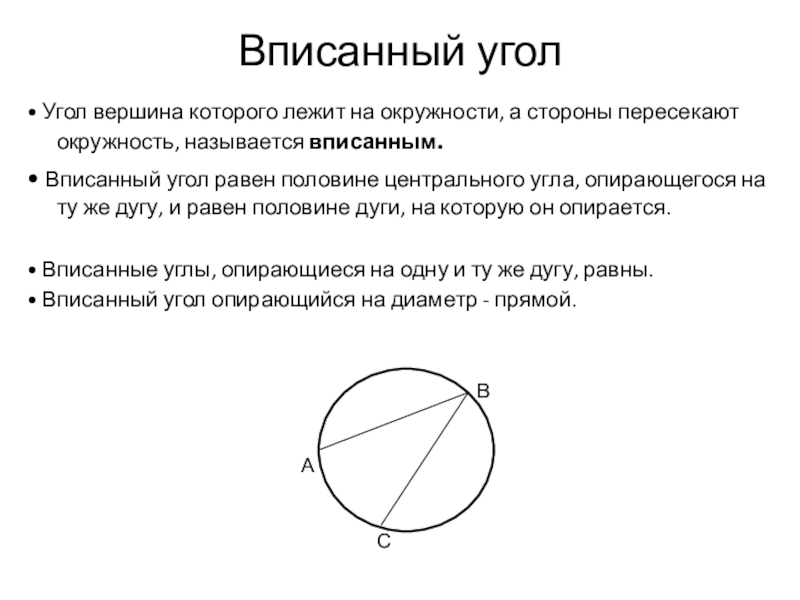
Слайд 19Вписанный угол
• Угол вершина которого лежит на окружности, а стороны
• Вписанный угол равен половине центрального угла, опирающегося на ту же дугу, и равен половине дуги, на которую он опирается.
• Вписанные углы, опирающиеся на одну и ту же дугу, равны.
• Вписанный угол опирающийся на диаметр - прямой.
А
В
С
Слайд 20
Если две хорды пересекаются, то произведение отрезков одной хорды равно произведению
CE*ED=AE*EB
Слайд 21
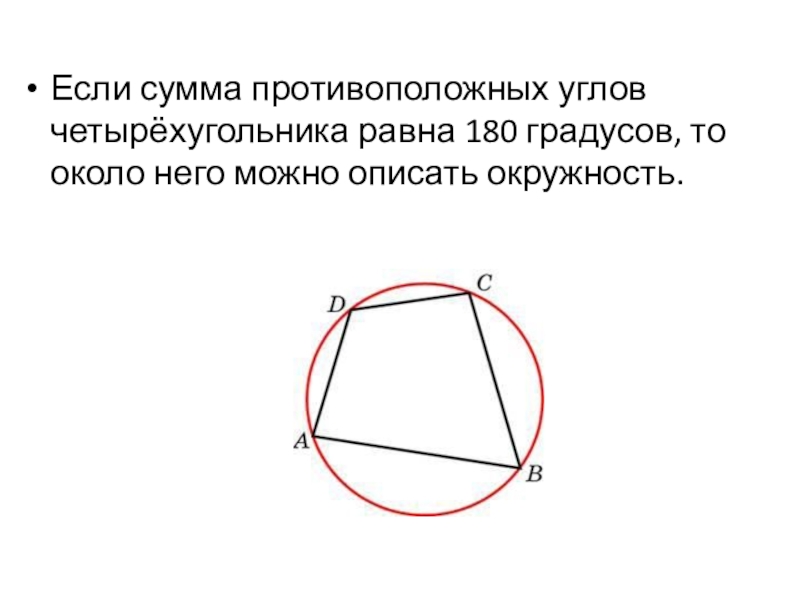
Если сумма противоположных углов четырёхугольника равна 180 градусов, то около него
Слайд 22
Величина угла, образованного пересекающимися хордами равна половине суммы величин дуг, заключённых
Слайд 24
Касательная к окружности перпендикулярна к радиусу, проведённому в точку касания.
Слайд 25
Отрезки касательных к окружности, проведённые из одной точки равны и составляют
Слайд 26
Если прямая проходит через конец радиуса, лежащего на окружности и перпендикулярна
Слайд 27
Величина угла, образованного касательной и хордой, имеющими общую точку на окружности
Слайд 28
Если из точки к окружности проведены касательная и секущая, то квадрат
Слайд 29
Величина угла, образованного касательной и секущей равна половине разности величин дуг,
Слайд 30
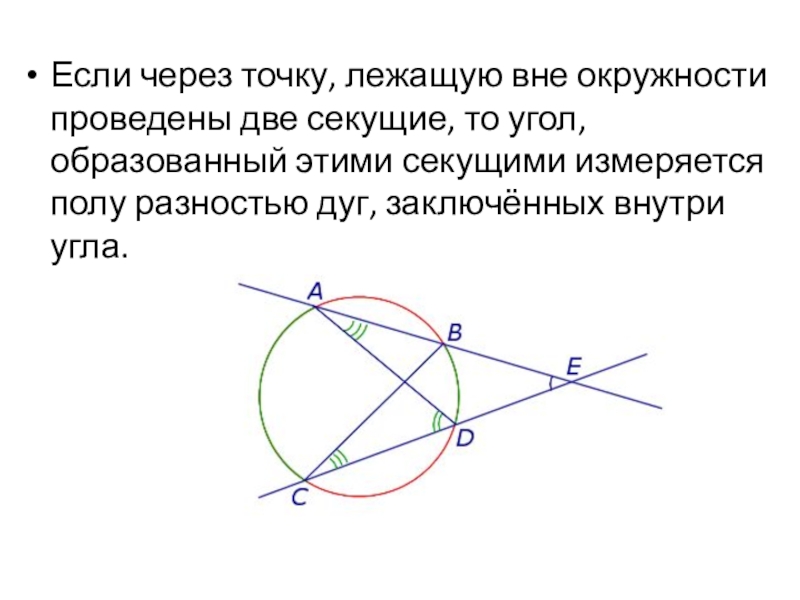
Если через точку, лежащую вне окружности проведены две секущие, то угол,
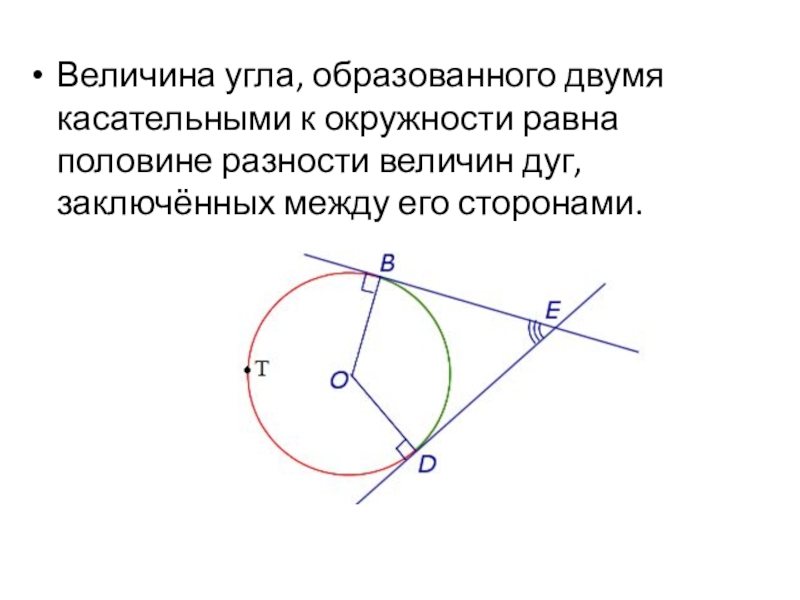
Слайд 31
Величина угла, образованного двумя касательными к окружности равна половине разности величин
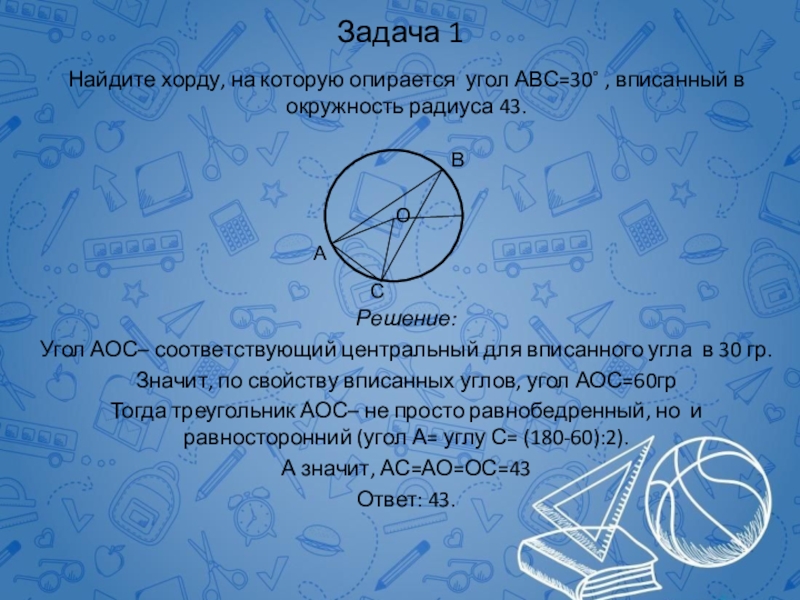
Слайд 33Задача 1
Найдите хорду, на которую опирается угол АВС=30˚ , вписанный в
Решение:
Угол АОС– соответствующий центральный для вписанного угла в 30 гр.
Значит, по свойству вписанных углов, угол АОС=60гр
Тогда треугольник АОС– не просто равнобедренный, но и равносторонний (угол А= углу С= (180-60):2).
А значит, АС=АО=ОС=43
Ответ: 43.
А
В
С
О
Слайд 35Задача 1
Найдите градусную меру угла АОС если, угол АВС=60 градусов.
А
В
С
О
Слайд 37Задача 3
Найдите градусную меру дуги, на которую опирается угол
Ответ: 82 градуса
А
В
С
Слайд 38Задача 2
Прямая касается окружности в точке K. Точка O — центр
Решение:
Угол, образованный хордой и касательной равен половине дуги, которую он заключает, поэтому величина дуги MK равна 2 · 83° = 166°. Угол MOK — центральный, поэтому он равен величине дуги, на которую опирается. Значит, угол MOK равен 166°. В треугольнике OMK стороны OK и OM равны как радиусы окружности, поэтому треугольник OMK — равнобедренный, следовательно, углы при основании равны. Сумма углов треугольника равна 180°, поэтому ∠OKM = ∠OMK = (180° − ∠KOM)/2 = (180° − 166°)/2 = 7°.
Ответ: 7.
О
М
К
Слайд 40Задача 1
Прямая касается окружности в точке K. Точка O — центр
Ответ: 15 градусов
М
К
О
Слайд 41Задача 2
Прямая касается окружности в точке K. Точка O — центр
Ответ: 61 градус.
О
К
М
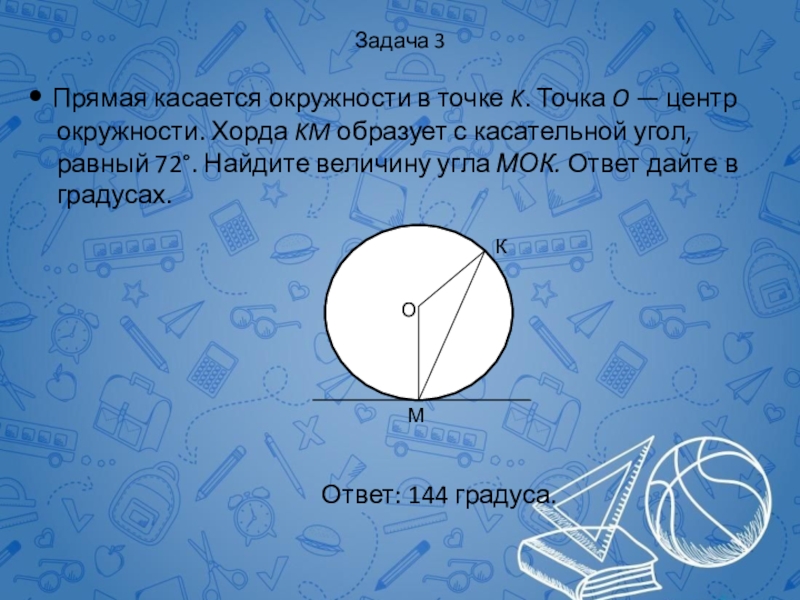
Слайд 42Задача 3
• Прямая касается окружности в точке K. Точка O —
Ответ: 144 градуса.
О
К
М
Слайд 43Задача 3
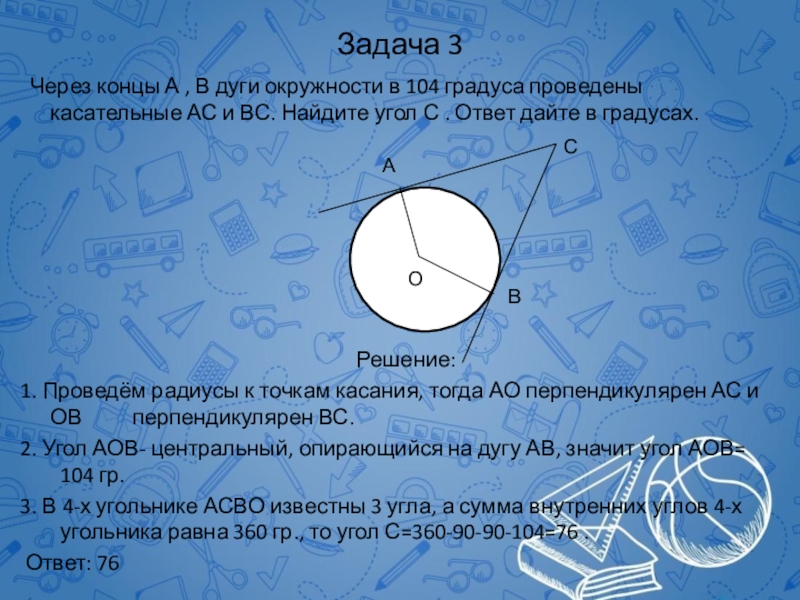
Через концы А , В дуги окружности в 104
Решение:
1. Проведём радиусы к точкам касания, тогда АО перпендикулярен АС и ОВ перпендикулярен ВС.
2. Угол АОВ- центральный, опирающийся на дугу АВ, значит угол АОВ= 104 гр.
3. В 4-х угольнике АСВО известны 3 угла, а сумма внутренних углов 4-х угольника равна 360 гр., то угол С=360-90-90-104=76 .
Ответ: 76
А
О
В
С
Слайд 45Задача 1
Через концы А , В дуги окружности в 110 градусов
Ответ: 70 градусов.
А
О
В
С
Слайд 46Задача 2
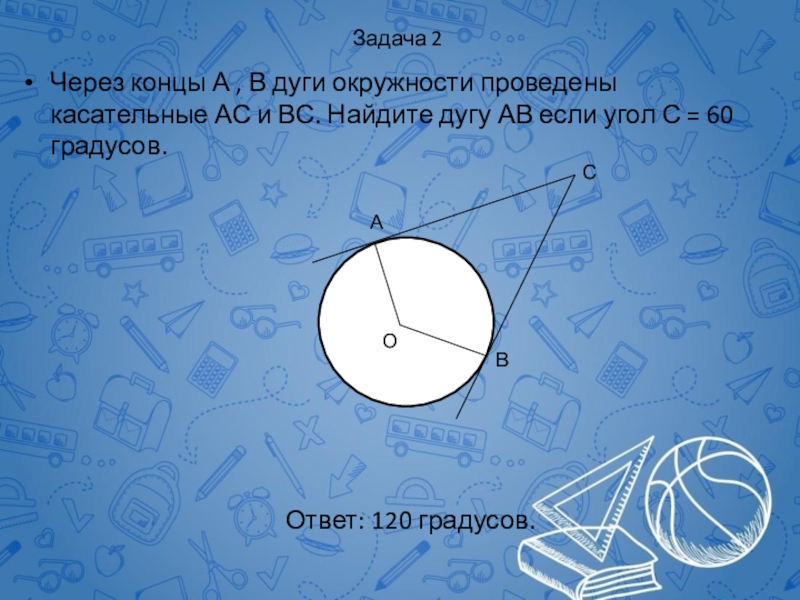
Через концы А , В дуги окружности проведены касательные
Ответ: 120 градусов.
А
С
В
О
Слайд 47Задача 3
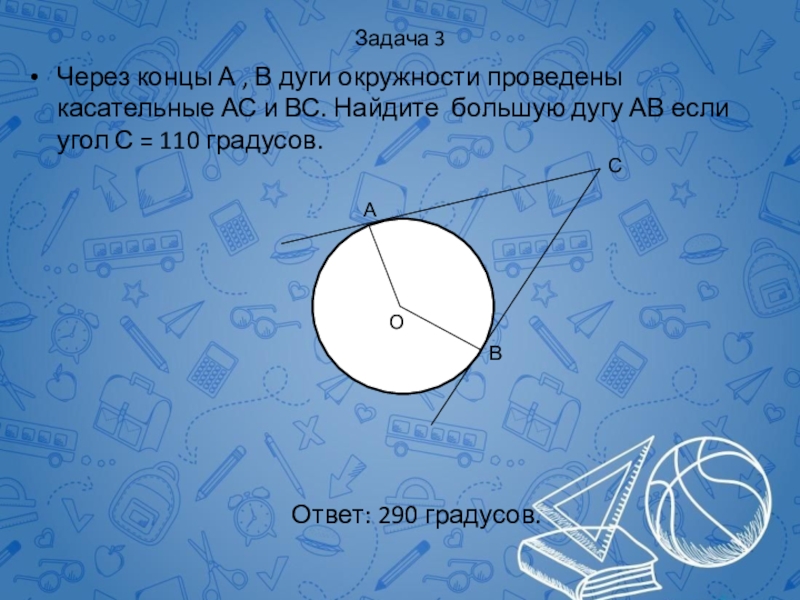
Через концы А , В дуги окружности проведены касательные АС
Ответ: 290 градусов.
А
С
В
О
Слайд 48Задача 4
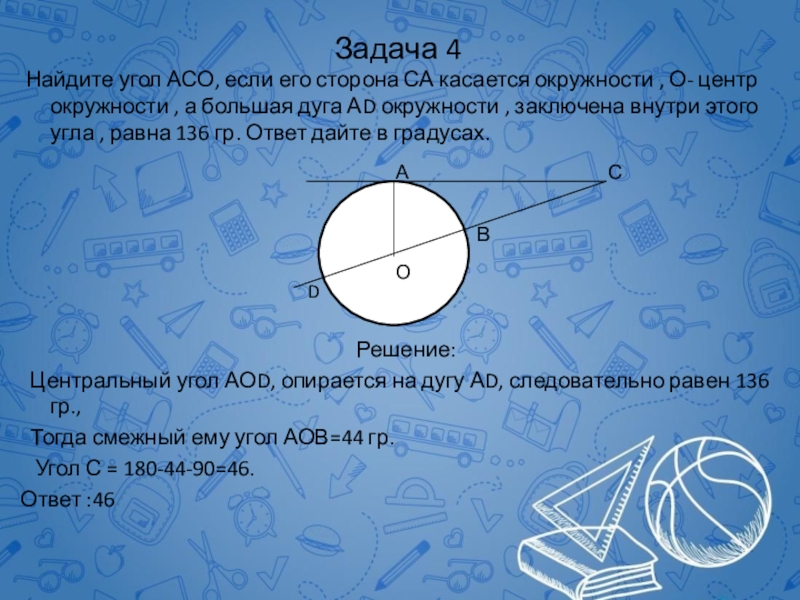
Найдите угол АСО, если его сторона СА касается окружности
Решение:
Центральный угол АОD, опирается на дугу АD, следовательно равен 136 гр.,
Тогда смежный ему угол АОВ=44 гр.
Угол С = 180-44-90=46.
Ответ :46
А
С
О
В
D
Слайд 50Задача 1
Найдите угол АСО, если его сторона СА касается окружности ,
Ответ: 34 градуса
А
С
О
В
D
Слайд 51Задача 2
Найдите угол АСО, если его сторона касается окружности, О-
Ответ: 23 градуса
А
С
О
В
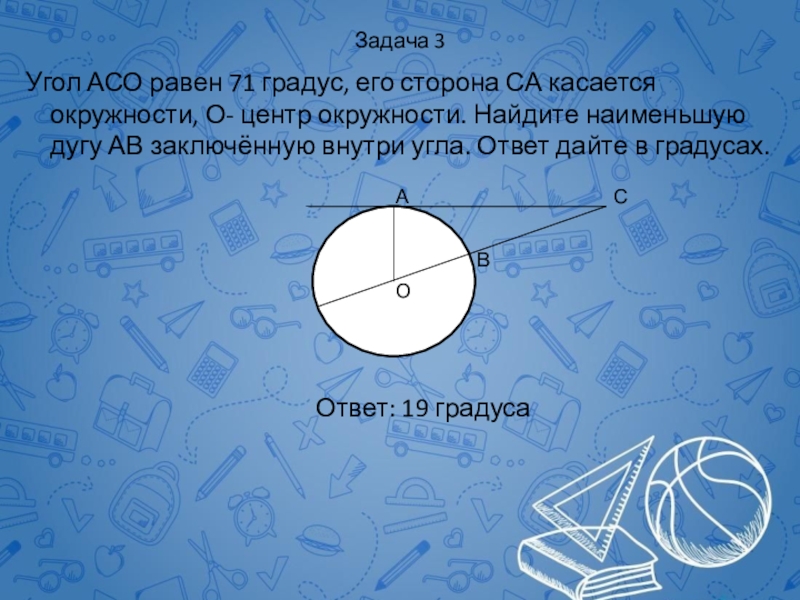
Слайд 52Задача 3
Угол АСО равен 71 градус, его сторона СА касается
Ответ: 19 градуса
А
С
О
В
Слайд 53Задача 5
В окружности с центром в точке О проведены диаметры
Решение:
Вписанные углы ВСD и ВАD опираются на одну и ту же дугу окружности, поэтому они равны. Тем самым, угол OAB = 30°.
Ответ: 30 градусов.
А
В
D
С
О
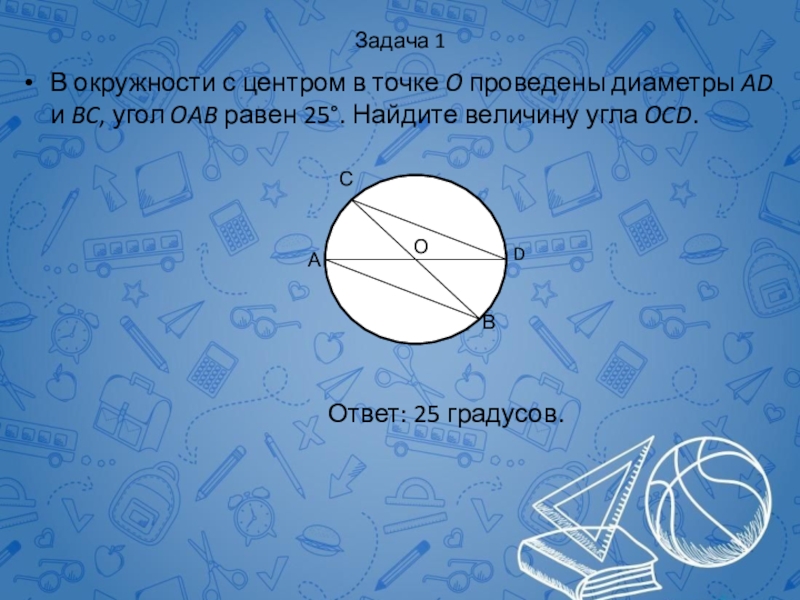
Слайд 55Задача 1
В окружности с центром в точке O проведены диаметры
Ответ: 25 градусов.
С
D
В
А
О
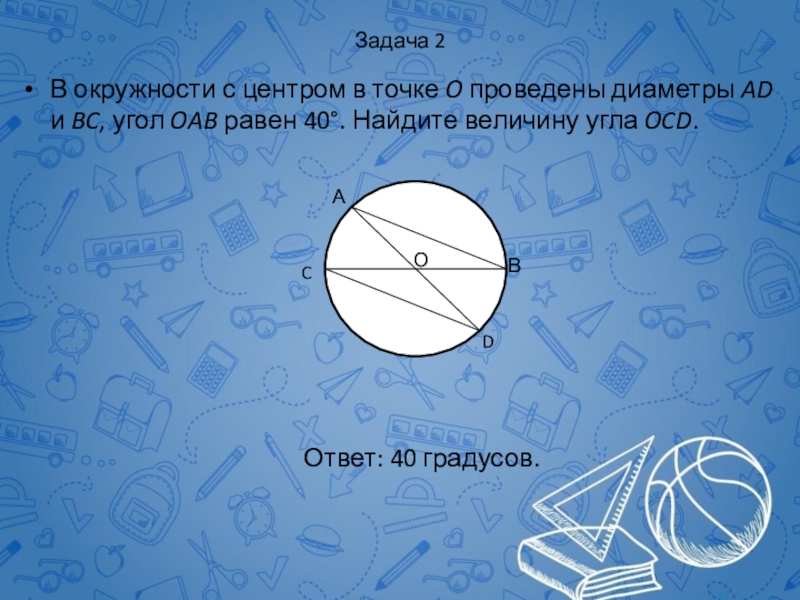
Слайд 56Задача 2
В окружности с центром в точке O проведены диаметры AD
Ответ: 40 градусов.
А
В
D
C
О
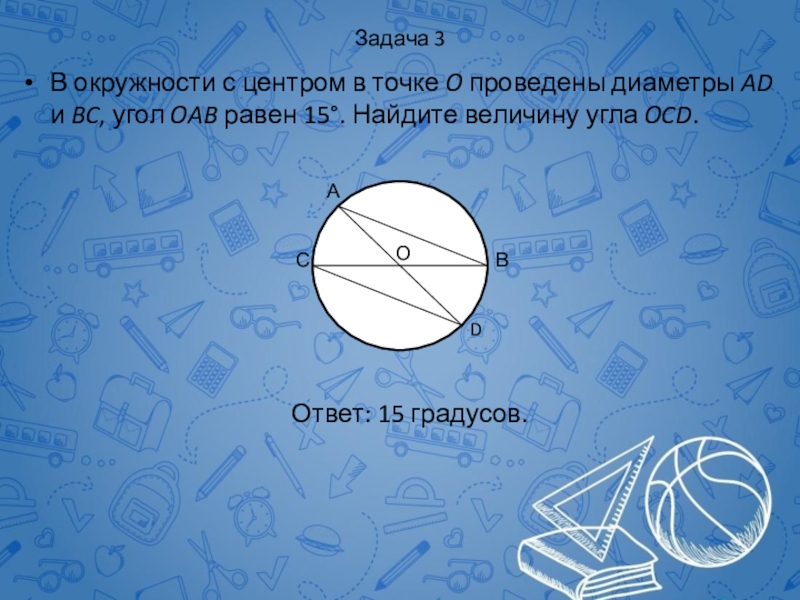
Слайд 57Задача 3
В окружности с центром в точке O проведены диаметры AD
Ответ: 15 градусов.
А
В
С
D
О
Слайд 58Задача 6
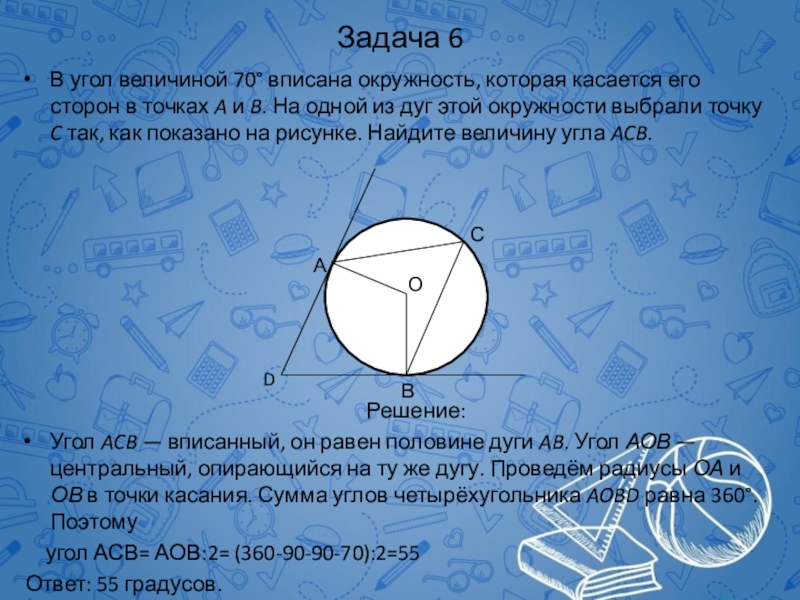
В угол величиной 70° вписана окружность, которая касается его сторон
Решение:
Угол ACB — вписанный, он равен половине дуги AB. Угол АОВ — центральный, опирающийся на ту же дугу. Проведём радиусы ОА и ОВ в точки касания. Сумма углов четырёхугольника AOBD равна 360°. Поэтому
угол АСВ= АОВ:2= (360-90-90-70):2=55
Ответ: 55 градусов.
А
D
В
С
О
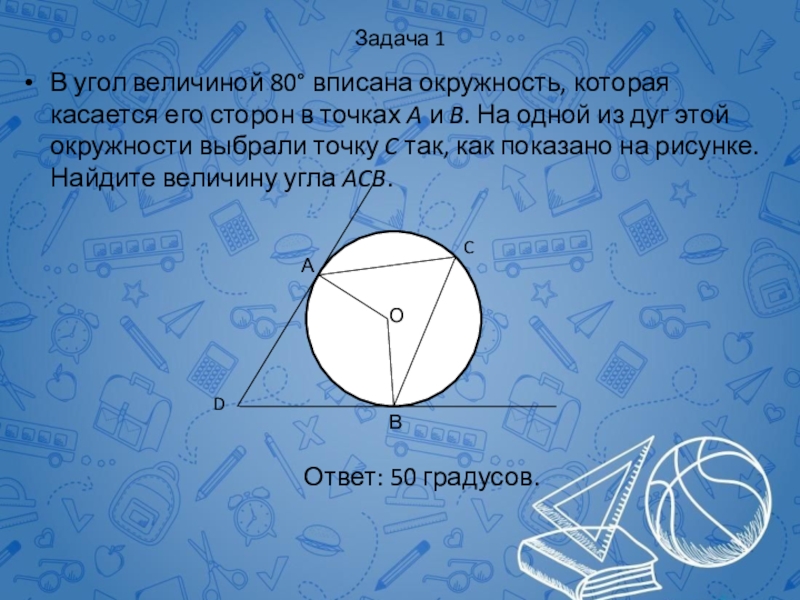
Слайд 60Задача 1
В угол величиной 80° вписана окружность, которая касается его сторон
Ответ: 50 градусов.
D
C
А
В
О
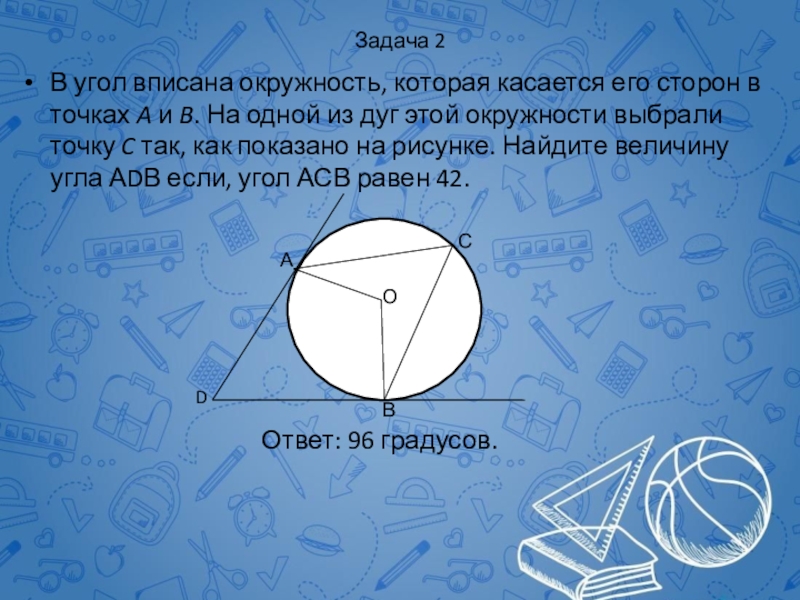
Слайд 61Задача 2
В угол вписана окружность, которая касается его сторон в
Ответ: 96 градусов.
С
А
О
В
D
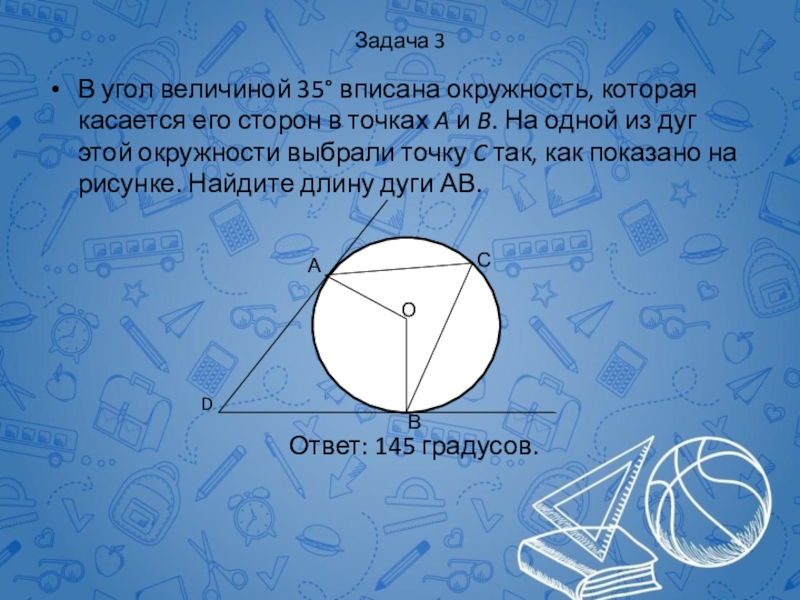
Слайд 62Задача 3
В угол величиной 35° вписана окружность, которая касается его сторон
Ответ: 145 градусов.
С
В
А
D
О
Слайд 63Задача 7
Касательные в точках A и B к окружности с
О
Решение:
Касательные, проведённые к окружности из одной точки равны, поэтому АС=ВС, следовательно, треугольник АВС- равнобедренный. Откуда угол САВ= углу СВА= (180- угол АСВ):2= 54 гр. Угол между касательной и хордой равен половине дуги, которую он опирается , значит, дуга АВ= 108 гр. Угол AOB — центральный, поэтому он равен дуге, на которую опирается, следовательно, равен 108°. Рассмотрим треугольник AOB, он равнобедренный, следовательно, угол ОАВ= углу АВО= (180-108):2=36гр
Ответ:36
А
В
С
О
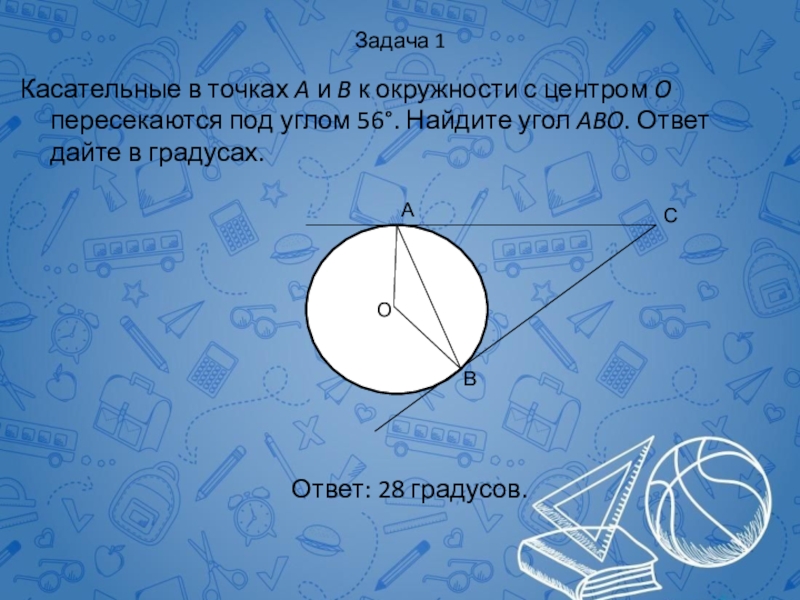
Слайд 65Задача 1
Касательные в точках A и B к окружности с центром
Ответ: 28 градусов.
А
О
В
С
Слайд 66Задача 2
Касательные в точках A и B к окружности с центром
Ответ: 7 градусов.
А
С
В
О
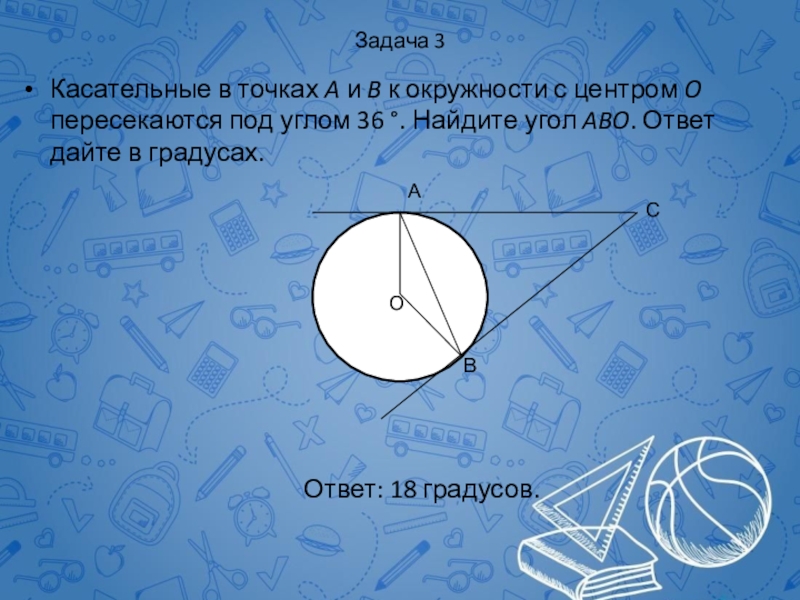
Слайд 67Задача 3
Касательные в точках A и B к окружности с центром
Ответ: 18 градусов.
А
О
В
С
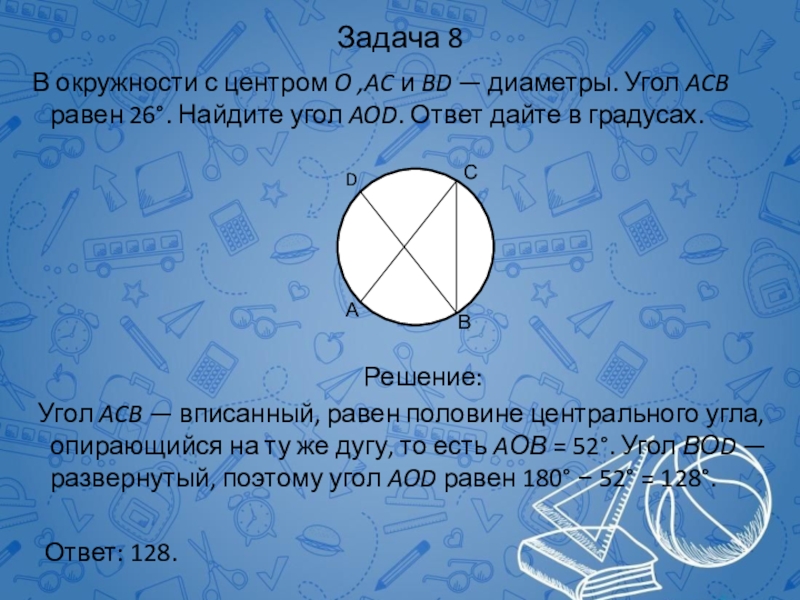
Слайд 68Задача 8
В окружности с центром O ,AC и BD —
Решение:
Угол ACB — вписанный, равен половине центрального угла, опирающийся на ту же дугу, то есть AОВ = 52°. Угол ВОD — развернутый, поэтому угол AOD равен 180° − 52° = 128°.
Ответ: 128.
А
С
В
D
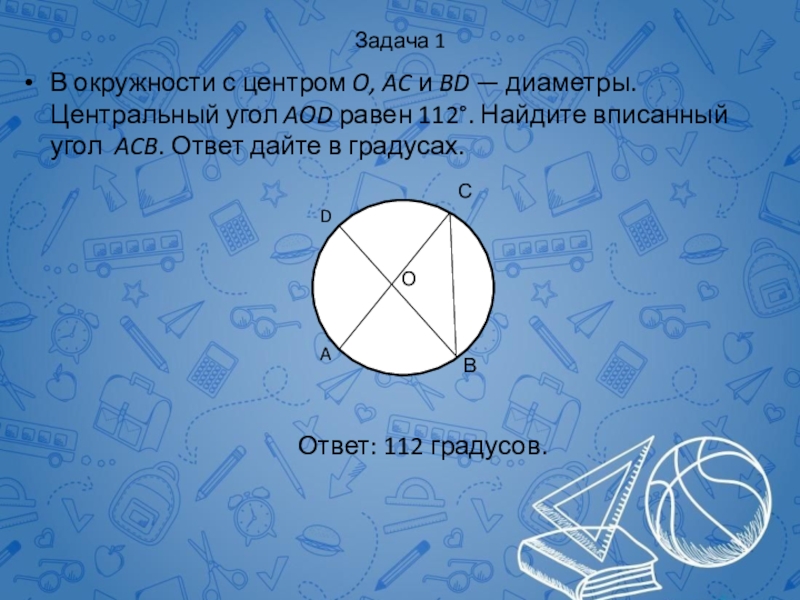
Слайд 70Задача 1
В окружности с центром O, AC и BD — диаметры. Центральный
Ответ: 112 градусов.
С
В
О
D
A
Слайд 71Задача 2
В окружности с центром О отрезки АС и ВD
Ответ: 21 градус.
А
С
В
D
О
Слайд 72Задача 3
В окружности с центром в точке О отрезки АС и
Ответ: 33 градуса.
А
С
В
D
O
Слайд 73Задача 9
В треугольнике ABC угол C равен 90°, AC = 30
Решение:
Вписанный прямой угол опирается на диаметр окружности, поэтому радиус окружности, описанной вокруг прямоугольного треугольника, равен половине гипотенузы. По теореме Пифагора имеем:
Ответ: 17.5
А
В
С
Слайд 75Задача 1
В треугольнике ABC угол C равен 90°, AC =
Ответ: 2.5
Слайд 76Справочные материалы.
1.) Геометрия. 7-9 классы: учеб. для общеобразоват. учреждений /Л.С. Атанасян,
2.) Сайт – «Решу ОГЭ»
3.) Открытый банк заданий.
4.) Геометрия: учеб. Для 7-9 кл. общеобразоват. учреждений / А.В. Погорелов. – 2-е изд. – М.: Просвещение, 2001.