или бегать на лыжах. Ему можно научиться только путем подражания или упражнения.
Д. Пойа
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Применение подобия треугольников к решению задач
Содержание
- 1. Презентация Применение подобия треугольников к решению задач
- 2. Тема урока Применение подобия треугольников к решению задач.
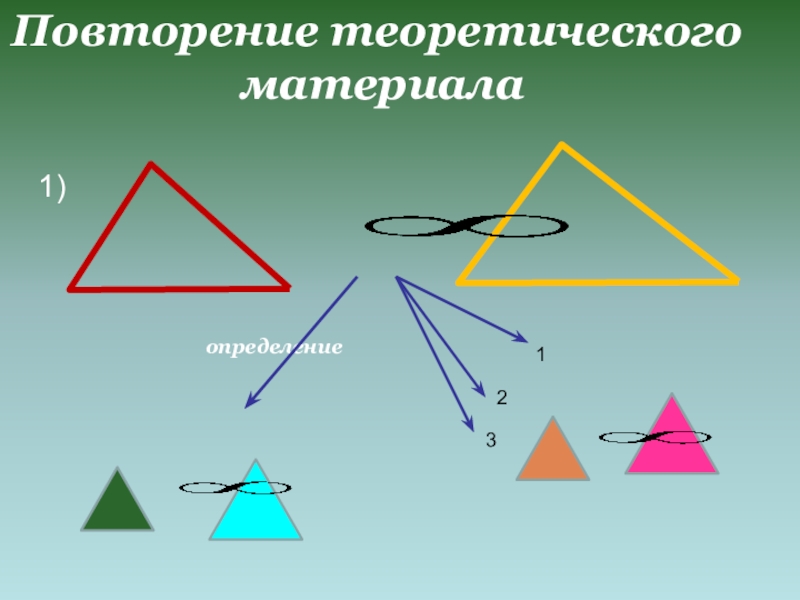
- 3. Повторение теоретического материалаопределение1231)
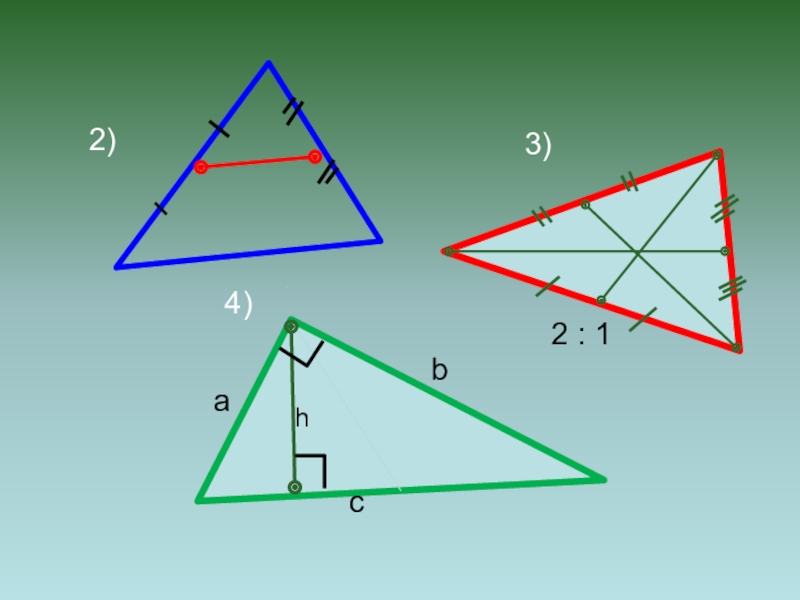
- 4. аbch2 : 12)3)4)
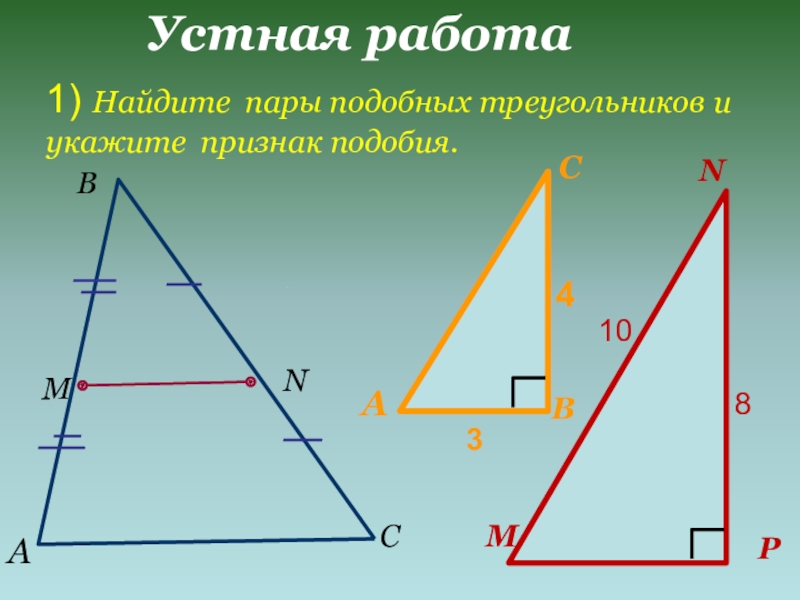
- 5. Устная работа1) Найдите пары подобных треугольников и укажите признак подобия.АВСМN34810АВСMNP
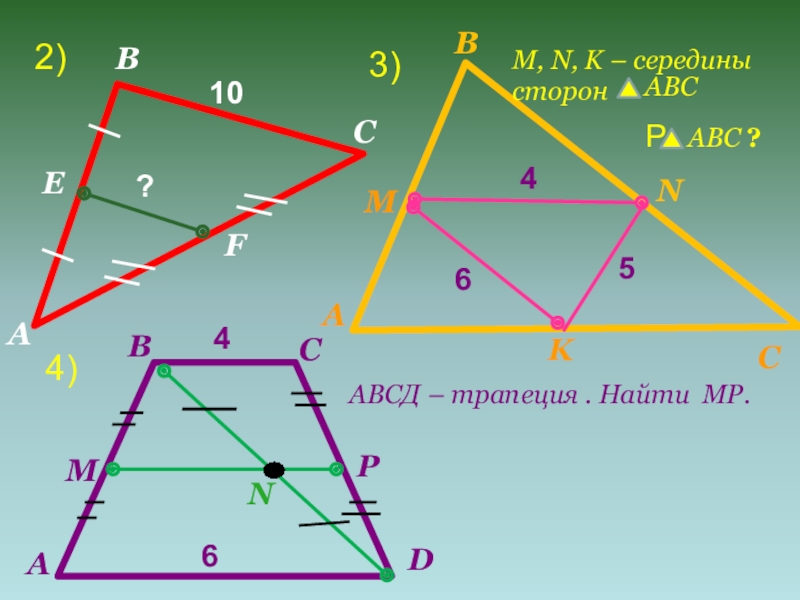
- 6. 2)АBCEF10?АBCMNK465M, N, K – середины сторон АВС PАВС ?АBCDMNP46АВСД – трапеция . Найти МР.3)4)
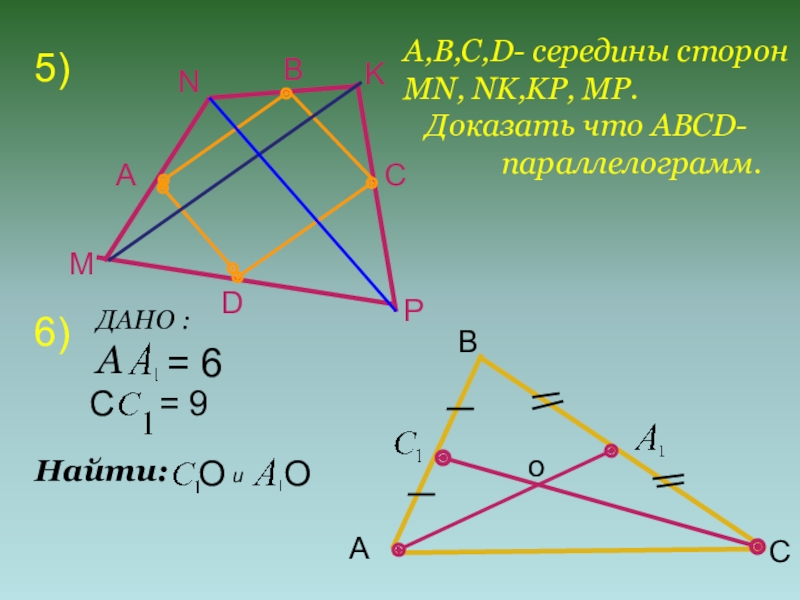
- 7. 5)МNKPАBCDА,В,С,D- середины сторон MN, NK,KP, MP.
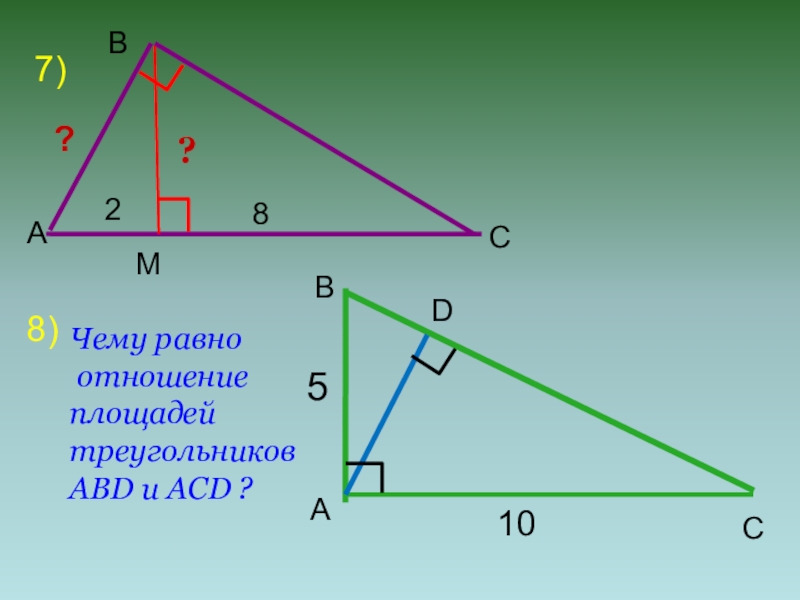
- 8. 7)МАBC?8)ABC28?D510Чему равно отношение площадей треугольниковABD и ACD ?
- 9. 1. Два треугольника подобны, если их углы
- 10. 3.Периметры подобных треугольников относятсякак квадраты сходственных сторон.
- 11. 5.Если отрезки гипотенузы, на которыеона делится высотой,
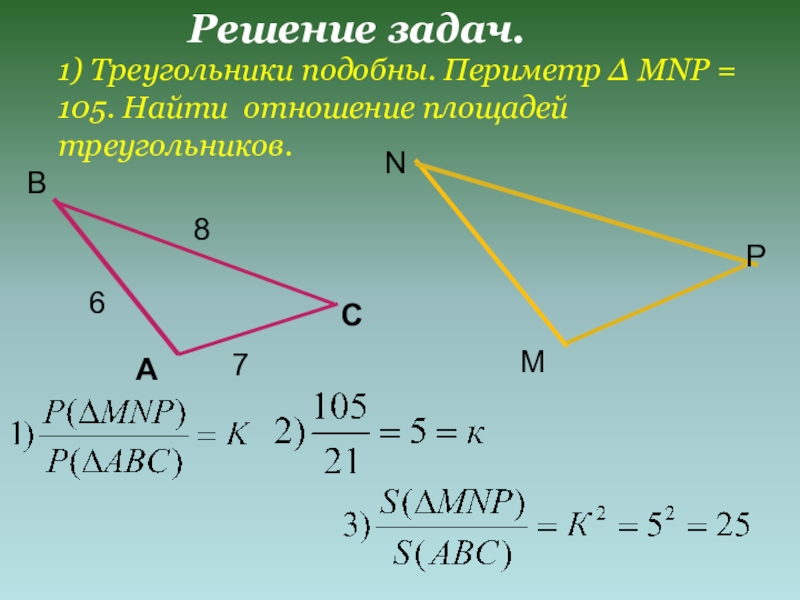
- 12. Решение задач.ABC687MNP1) Треугольники подобны. Периметр Δ MNP = 105. Найти отношение площадей треугольников.
- 13. Решение задач.ABC2) В прямоугольном треугольнике ABC
Тема урока Применение подобия треугольников к решению задач.
Слайд 1Классная работа
10.02.2012г.
Умение решать задачи- такое же практическое искусство, как умение плавать
Слайд 5Устная работа
1) Найдите пары подобных треугольников и
укажите признак подобия.
А
В
С
М
N
3
4
8
10
А
В
С
M
N
P
Слайд 62)
А
B
C
E
F
10
?
А
B
C
M
N
K
4
6
5
M, N, K – середины
сторон
АВС
P
АВС ?
А
B
C
D
M
N
P
4
6
АВСД
– трапеция . Найти МР.
3)
4)
Слайд 75)
М
N
K
P
А
B
C
D
А,В,С,D- середины сторон
MN, NK,KP, MP.
Доказать что ABCD-
параллелограмм.
6)
A
B
C
O
o
А
= 6
C
= 9
ДАНО :
Найти:
O
и
Слайд 91. Два треугольника подобны, если их углы
соответственно равны и сходственные
стороны пропорциональны.
1.Если три стороны одного треугольника
соответственно пропорциональны трем сторонам
другого треугольника, то треугольники подобны.
2. Стороны одного треугольника имеют длины
3см, 4см, 6см, стороны другого - 9см,14см,18см.
Подобны ли эти треугольники?
Тест на установление истинности
или ложности
2. Два равносторонних треугольника
всегда подобны.
Слайд 10
3.Периметры подобных треугольников относятся
как квадраты сходственных сторон.
3. Если два угла
одного треугольника
равны 60° и 50°, а два угла другого треугольника
равны 50° и 80°, то такие треугольники подобны.
равны 60° и 50°, а два угла другого треугольника
равны 50° и 80°, то такие треугольники подобны.
4. Два прямоугольных треугольника подобны,
если имеют по равному острому углу.
4. Два равнобедренных треугольника подобны,
если их боковые стороны пропорциональны.
Слайд 11
5.Если отрезки гипотенузы, на которые
она делится высотой, проведенной из
вершины прямого
угла равны 2 и 8 см,
то это высота равна 4 см.
то это высота равна 4 см.
5. Если медиана треугольника равна 9см,
то расстояние от вершины треугольника
до точки пересечения медиан равна 6см
да
да
да
нет
нет
да
да
нет
нет
да
Слайд 12
Решение задач.
A
B
C
6
8
7
M
N
P
1) Треугольники подобны. Периметр Δ MNP = 105. Найти
отношение площадей треугольников.
Слайд 13
Решение задач.
A
B
C
2) В прямоугольном треугольнике ABC к гипотенузе AC проведена
высота BD, BC=2 см, AD=3см. Найдите DC, BD, AB.
D
2
3
х
4= 3х+х²,
х²+3х-4=0,
х=-4; х=1. DC=1см
=2√3 см
