10 – 11.
Авторы: Л.С. Атанасян и другие.
10 класс
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Правильная пирамида разработана для урока математики в 10 классе по учебнику Л.С. Атанасяна.
Содержание
- 1. Презентация Правильная пирамида разработана для урока математики в 10 классе по учебнику Л.С. Атанасяна.
- 2. ПИРАМИДА. Правильная пирамида
- 3. Продолжите предложения:
- 4. SABCDOE1)Δ ABD– прямоугольный, где ABD =
- 5. BACDM45º12смMD=AD=AB=x, DB2=2AD2, MB2=MD2+DB2; 144= 2x2+x2, x2=48,x=4√3см, MD=
- 6. Свойства пирамид, имеющих равные боковые рёбраЕсли у
- 7. Свойства пирамид, имеющих равные апофемыЕсли у
- 8. SABCDOEПирамида называется правильной, если
- 9. SABCDOEВсе боковые рёбра правильной пирамиды равны, а боковые грани являются равными равнобедренными треугольниками.
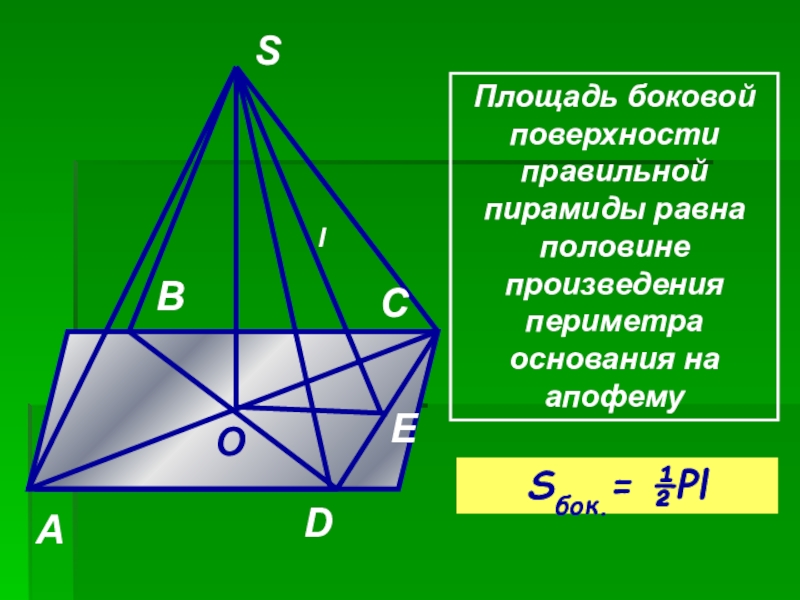
- 10. SABCDOEПлощадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофемуSбок.= ½Pll
- 11. Продолжите предложения.
- 12. Контрольные вопросы
- 13. 4.Вершина пирамиды проецируется в точку пересечения диагоналей
- 14. КОНТРОЛЬНЫ Й ТЕСТ
- 15. 4. Чему равна апофема правильной четырёхугольной пирамиды
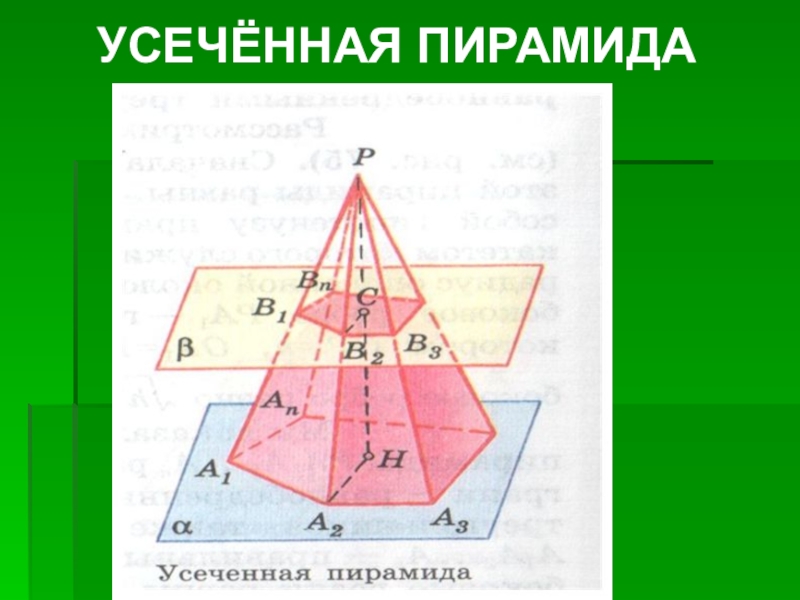
- 16. УСЕЧЁННАЯ ПИРАМИДА
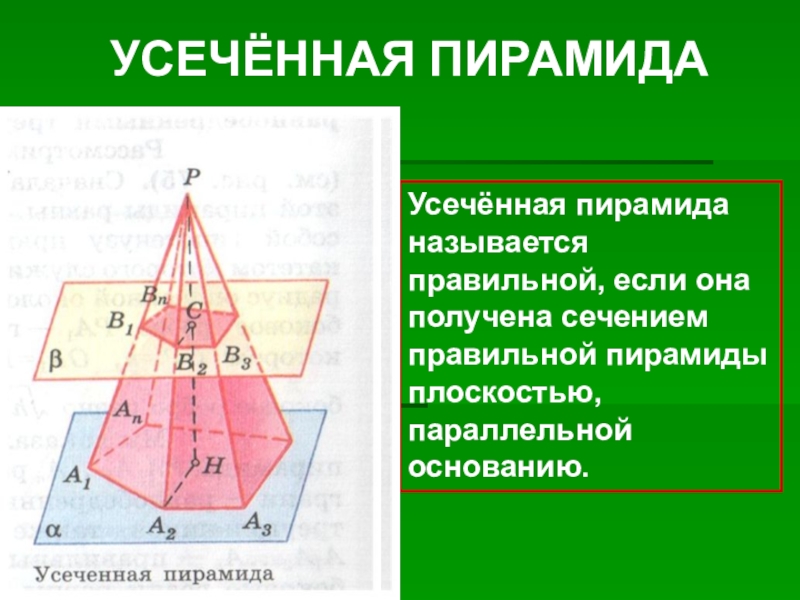
- 17. Усечённая пирамида называется правильной, если она получена сечением правильной пирамиды плоскостью, параллельной основанию.УСЕЧЁННАЯ ПИРАМИДА
- 18. Площадь боковой поверхности усечённой пирамиды равна сумме
ПИРАМИДА. Правильная пирамида
Слайд 1Презентация по геометрии учителя математики МКОУ СОШ №1 Розовой С М пгт. Палана Камчатский край Учебник геометрии
Слайд 3Продолжите предложения: 1.
Пирамидой называется многогранник… 2.Высотой пирамиды называется… 3. Площадь полной поверхности пирамиды равна … 4. Площадь боковой поверхности пирамиды равна …
Слайд 4
S
A
B
C
D
O
E
1)Δ ABD– прямоугольный, где ABD = BDC= 90º.
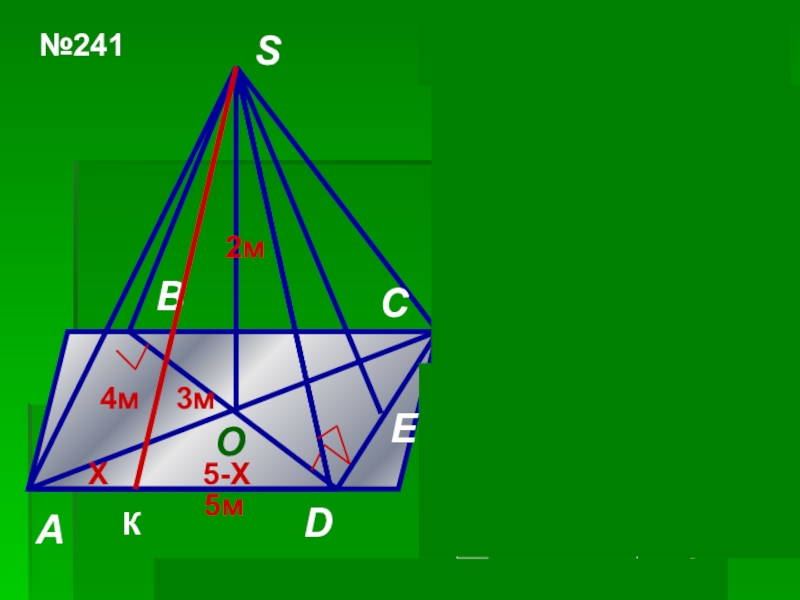
№241
5м
4м
3м
2) Sосн.=2·½·BD·CD=
12м2; SD2 = SO2+OD2=6,25, SD=2,5м. SΔSDC=½SD·CD= 5м2;
2м
К
3) AC2+BD2=2(AB2+AD2), AC2+9=2(16+25), AC2=73, AC =√73м; SA2=SO2+AO2=89/4,
4)SK2=AS2-AK2=SD2-KD2, 89/4-х2=25/4- (5-х)2, х =4,1; SK2=22,25 – 4,12=5,44, SK=2√34/5м; SΔSAD=½AD·SK=½·5·2√34/5==√34м2
X
5-X
Sп.п.=Sб.+Sосн. = 5·2+2·√34+12 = 22+2√34м2
Слайд 5
B
A
C
D
M
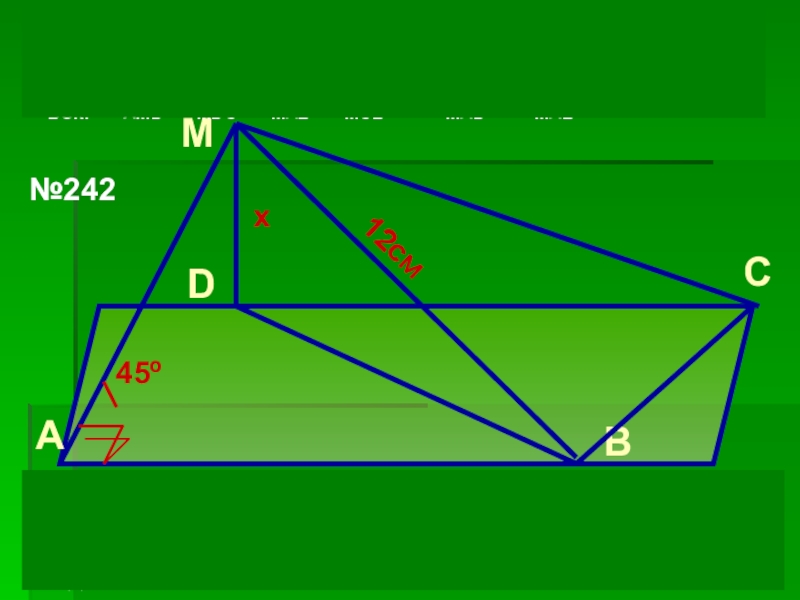
45º
12см
MD=AD=AB=x, DB2=2AD2, MB2=MD2+DB2; 144= 2x2+x2, x2=48,x=4√3см, MD= AB=AD=4√3см. SБОК.=SAMD+SMDC+SMAB+SMCB = 2SMAD+2SMAB
x
№242
SMAD=½AD·MD=½·4√3·4√3=24см2;
MA2=MB2-AB2, MA=4√6; SMAB=½MA·AB=½·4√3·4√6=24√2см2. Sбок.= 2·24+2·24√2=48+48√2cм2
Слайд 6Свойства пирамид, имеющих равные боковые рёбра
Если у пирамиды равны боковые рёбра,
то:
1) вершина пирамиды проецируется в центр описанной около основания окружности; для прямоугольного треугольника – это середина гипотенузы;
2) боковые рёбра составляют с плоскостью основания равные углы; 3) боковые рёбра составляют с высотой равные углы; верно и обратное.
1) вершина пирамиды проецируется в центр описанной около основания окружности; для прямоугольного треугольника – это середина гипотенузы;
2) боковые рёбра составляют с плоскостью основания равные углы; 3) боковые рёбра составляют с высотой равные углы; верно и обратное.
Слайд 7Свойства пирамид, имеющих равные апофемы
Если у пирамиды равны апофемы, то:
1)
вершина пирамиды проецируется в центр вписанной в основание окружности;
2) двугранные углы при рёбрах основания равны;
3) апофемы составляют с высотой пирамиды равные углы; верно и обратное.
2) двугранные углы при рёбрах основания равны;
3) апофемы составляют с высотой пирамиды равные углы; верно и обратное.
Слайд 8
S
A
B
C
D
O
E
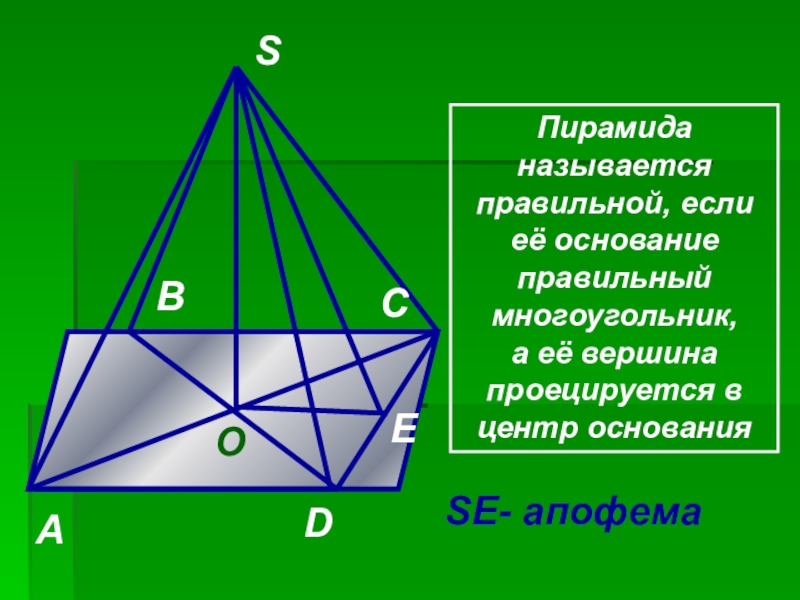
Пирамида называется правильной, если её
основание правильный многоугольник, а её вершина проецируется в центр основания
SE- апофема
Слайд 9
S
A
B
C
D
O
E
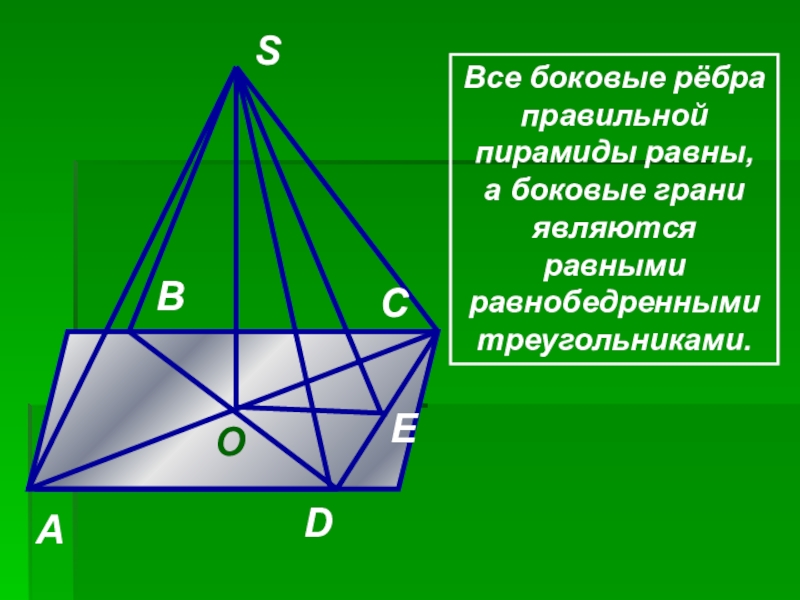
Все боковые рёбра правильной пирамиды равны, а боковые грани являются
равными равнобедренными треугольниками.
Слайд 10
S
A
B
C
D
O
E
Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на
апофему
Sбок.= ½Pl
l
Слайд 11Продолжите предложения.
У правильной пирамиды: 1) боковые рёбра… 2) боковые грани… 3) апофемы … 4) двугранные углы при основании… 5) каждая точка высоты равноудалена от всех … основания; 6) боковыми гранями являются…
Слайд 12Контрольные вопросы
1.Боковые ребра пирамиды равны между собой. Может ли основание пирамиды быть : 1) ромбом; 2) прямоугольником; 3) правильным шестиугольником?
2. Боковые ребра пирамиды равны между собой. Где находится проекция вершины пирамиды на основании, если основание: 1) прямоугольник;
2) прямоугольный треугольник?
3.Двугранные углы при основании пирамиды равны между собой. Может ли в основании пирамиды быть: 1) ромб; 2) прямоугольник; 3) правильный шестиугольник; 4) равнобедренный треугольник?
2. Боковые ребра пирамиды равны между собой. Где находится проекция вершины пирамиды на основании, если основание: 1) прямоугольник;
2) прямоугольный треугольник?
3.Двугранные углы при основании пирамиды равны между собой. Может ли в основании пирамиды быть: 1) ромб; 2) прямоугольник; 3) правильный шестиугольник; 4) равнобедренный треугольник?
Слайд 134.Вершина пирамиды проецируется в точку пересечения диагоналей основания. Что можно сказать
о двугранных углах при основании пирамиды, если основание: 1) ромб; 2) параллелограмм; 3) равнобедренная трапеция?
5. Основанием пирамиды служит прямоугольный треугольник. Медиана, проведенная к гипотенузе треугольника, равна 6см. Найти высоту пирамиду.
6. Основанием пирамиды служит ромб. Двугранные углы при ребрах пирамиды равны по 45º. Найдите высоту пирамиды, если высота ромба равна 6см.
5. Основанием пирамиды служит прямоугольный треугольник. Медиана, проведенная к гипотенузе треугольника, равна 6см. Найти высоту пирамиду.
6. Основанием пирамиды служит ромб. Двугранные углы при ребрах пирамиды равны по 45º. Найдите высоту пирамиды, если высота ромба равна 6см.
Слайд 14КОНТРОЛЬНЫ Й ТЕСТ
«ПРАВИЛЬНАЯ ПИРАМИДА»
1. Чему равна высота правильной треугольной пирамиды со стороной основания а и боковым ребром b?
2. Чему равна сторона основания правильной треугольной пирамиды, если её высота равна h и боковое ребро b?
3. Чему равна апофема правильной четырёхугольной пирамиды со стороной основания а и высотой h?
1. Чему равна высота правильной треугольной пирамиды со стороной основания а и боковым ребром b?
2. Чему равна сторона основания правильной треугольной пирамиды, если её высота равна h и боковое ребро b?
3. Чему равна апофема правильной четырёхугольной пирамиды со стороной основания а и высотой h?
Слайд 154. Чему равна апофема правильной четырёхугольной пирамиды со стороной основания а
и боковым ребром b?
5. Чему равна сторона основания правильной шестиугольной пирамиды ,если её высота равна h и боковое ребро b?
6. Чему равна высота правильной шестиугольной пирамиды со стороной основания а и боковым ребром b?
5. Чему равна сторона основания правильной шестиугольной пирамиды ,если её высота равна h и боковое ребро b?
6. Чему равна высота правильной шестиугольной пирамиды со стороной основания а и боковым ребром b?
Слайд 17Усечённая пирамида называется правильной, если она получена сечением правильной пирамиды плоскостью,
параллельной основанию.
УСЕЧЁННАЯ ПИРАМИДА
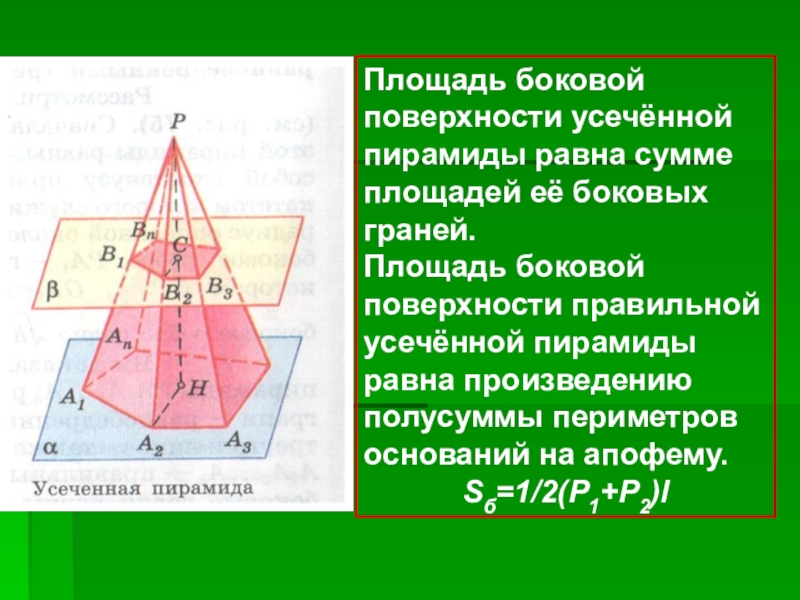
Слайд 18Площадь боковой поверхности усечённой пирамиды равна сумме площадей её боковых граней.
Площадь
боковой поверхности правильной усечённой пирамиды равна произведению полусуммы периметров оснований на апофему.
Sб=1/2(Р1+Р2)l
Sб=1/2(Р1+Р2)l
