а другое - деление отрезка в среднем и крайнем отношении… Первое можно сравнить с мерой золота; второе же больше напоминает драгоценный камень”.
Иоганн Кеплер
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Практическое применение теоремы Пифагора
Содержание
- 1. Презентация Практическое применение теоремы Пифагора
- 2. Практическое применение теоремы Пифагора
- 3. Диагональ d квадрата со стороной
- 4. Диагональ d прямоугольника со сторонами а и
- 5. На рисунке изображен куб, внутри которого проведена
- 6. Рассуждение, подобное этому, можно провести и для
- 7. Считать приложения теоремы Пифагора
- 8. В романской архитектуре часто встречается
- 9. В конце девятнадцатого века высказывались
- 10. Пифагоровы тройки
- 11. Изучение свойств натуральных чисел привело
- 12. Сегодня эта задача именуется задачей
- 13. Эти тройки можно найти по формулам: b=(a2-1)/2,
- 14. Древневавилонский клинописный текст, содержащий 15 наборов пифагоровых
- 15. И тем не менее вопрос
- 16. “Геометрия владеет двумя сокровищами: одно из них
- 17. Спасибо за внимание
Практическое применение теоремы Пифагора
Слайд 3 Диагональ d квадрата со стороной а можно рассматривать как
гипотенузу прямоугольного равнобедренного треугольника с катетом а. Таким образом:
d2=2a², d= a.
d2=2a², d= a.
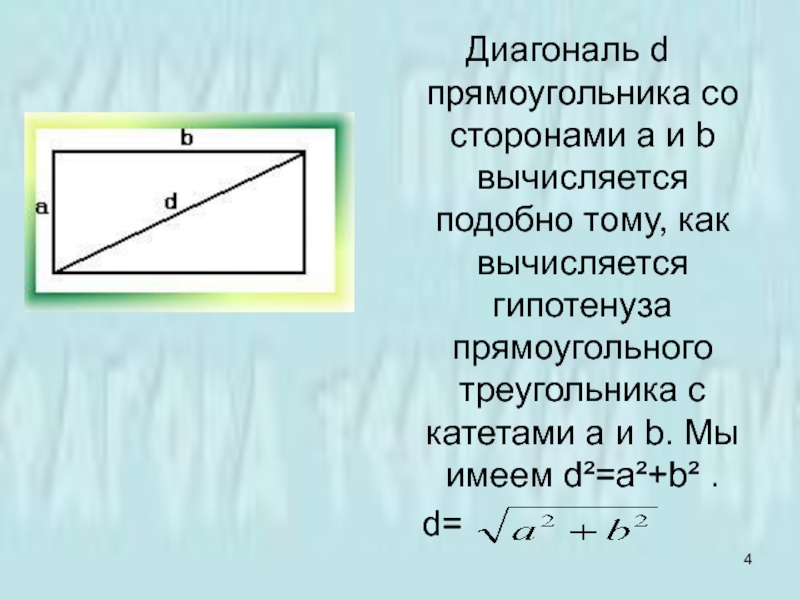
Слайд 4Диагональ d прямоугольника со сторонами а и b вычисляется подобно тому,
как вычисляется гипотенуза прямоугольного треугольника с катетами a и b. Мы имеем d²=a²+b² .
d=
d=
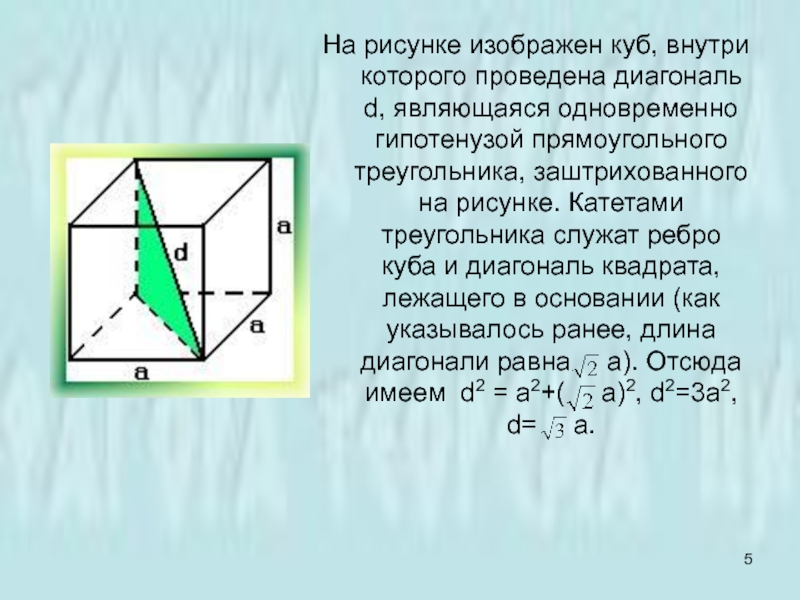
Слайд 5На рисунке изображен куб, внутри которого проведена диагональ d, являющаяся одновременно
гипотенузой прямоугольного треугольника, заштрихованного на рисунке. Катетами треугольника служат ребро куба и диагональ квадрата, лежащего в основании (как указывалось ранее, длина диагонали равна а). Отсюда имеем d2 = a2+( а)2, d2=3a2, d= a.
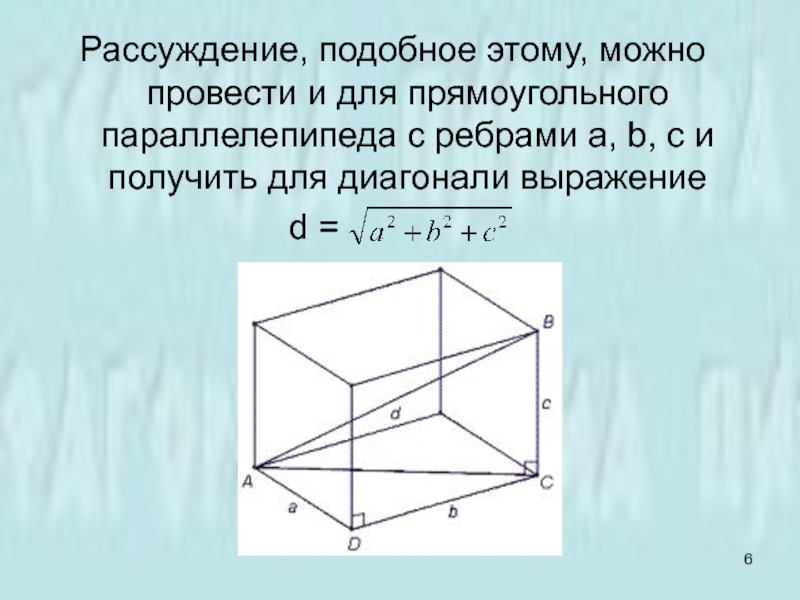
Слайд 6Рассуждение, подобное этому, можно провести и для прямоугольного параллелепипеда с ребрами
a, b, с и получить для диагонали выражение
d =
d =
Слайд 7 Считать приложения теоремы Пифагора только теоретическими - большая
ошибка. Заметим, что расчёт площади кровли можно заметно упростить, если воспользоваться одним очень простым правилом, справедливым во всех случаях, когда все скаты крыши, сколько бы их ни было, имеют одинаковый уклон. Оно гласит: "Чтобы найти поверхность крыши, все скаты которой имеют равный уклон, нужно умножить перекрываемую площадь на длину какого-нибудь стропила и разделить полученное произведение на проекцию этого стропила на перекрываемую площадь."
Слайд 8 В романской архитектуре часто встречается мотив, представленный на рисунке.
Если b по-прежнему обозначает ширину окна, то радиусы полуокружностей будут равны R = b / 2 и
r = b / 4. Радиус p внутренней окружности можно вычислить из прямоугольного треугольника, изображенного на рис. пунктиром p=b/6.
r = b / 4. Радиус p внутренней окружности можно вычислить из прямоугольного треугольника, изображенного на рис. пунктиром p=b/6.
Слайд 9 В конце девятнадцатого века высказывались разнообразные предположения о существовании
обитателей Марса подобных человеку, это явилось следствием открытий итальянского астронома Скиапарелли.
Естественно, что вопрос о том, можно ли с помощью световых сигналов объясняться с этими гипотетическими существами, вызвал оживленную дискуссию. Парижской академией наук была даже установлена премия в 100000 франков тому, кто первый установит связь с каким-нибудь обитателем другого небесного тела; эта премия все ещё ждет счастливца. В шутку, хотя и не совсем безосновательно, было решено передать обитателям Марса сигнал в виде теоремы Пифагора.
Неизвестно, как это сделать; но для всех очевидно, что математический факт, выражаемый теоремой Пифагора, имеет место всюду и поэтому похожие на нас обитатели другого мира должны понять такой сигнал.
Естественно, что вопрос о том, можно ли с помощью световых сигналов объясняться с этими гипотетическими существами, вызвал оживленную дискуссию. Парижской академией наук была даже установлена премия в 100000 франков тому, кто первый установит связь с каким-нибудь обитателем другого небесного тела; эта премия все ещё ждет счастливца. В шутку, хотя и не совсем безосновательно, было решено передать обитателям Марса сигнал в виде теоремы Пифагора.
Неизвестно, как это сделать; но для всех очевидно, что математический факт, выражаемый теоремой Пифагора, имеет место всюду и поэтому похожие на нас обитатели другого мира должны понять такой сигнал.
Слайд 11 Изучение свойств натуральных чисел привело пифагорейцев к ещё одной
«вечной» проблеме теоретической арифметики (теории чисел) — проблеме, ростки которой пробивались задолго до Пифагора в Древнем Египте и Древнем Вавилоне, а общее решение не найдено и поныне. Начнем с задачи, которую в современных терминах можно сформулировать так: решить в натуральных числах неопределенное уравнение
а2+b2=c2.
а2+b2=c2.
Слайд 12 Сегодня эта задача именуется задачей Пифагора, а её решения
— тройки натуральных чисел, удовлетворяющих уравнению (а2+b2=c2)— называются пифагоровыми тройками. В силу очевидной связи теоремы Пифагора с задачей Пифагора последней можно дать геометрическую формулировку: найти все прямоугольные треугольники с целочисленными катетами а, b и целочисленной гипотенузой c.
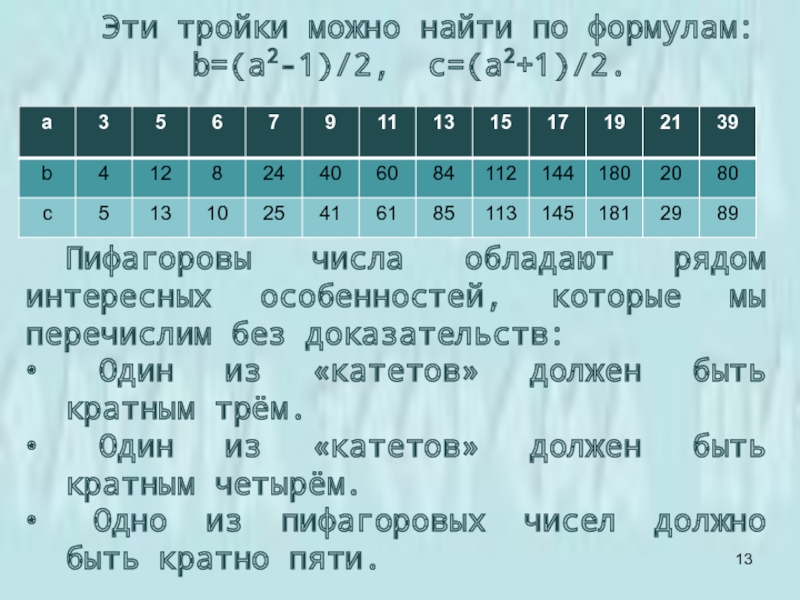
Слайд 13Эти тройки можно найти по формулам:
b=(a2-1)/2, c=(a2+1)/2.
Пифагоровы числа обладают рядом интересных
особенностей, которые мы перечислим без доказательств:
Один из «катетов» должен быть кратным трём.
Один из «катетов» должен быть кратным четырём.
Одно из пифагоровых чисел должно быть кратно пяти.
Один из «катетов» должен быть кратным трём.
Один из «катетов» должен быть кратным четырём.
Одно из пифагоровых чисел должно быть кратно пяти.
Слайд 14Древневавилонский клинописный текст, содержащий 15 наборов пифагоровых троек, среди которых (четвёртая
строка) есть тройка 12709, 13500, 18541:
12709 + 13500 = 18541.
Нью-Йорк. Плимптоновский фонд библиотеки
Колумбийского университета.
12709 + 13500 = 18541.
Нью-Йорк. Плимптоновский фонд библиотеки
Колумбийского университета.
Слайд 15 И тем не менее вопрос об общем решении уравнения
(а2+b2=c2) в натуральных числах был поставлен и решён только пифагорейцами. Общая постановка, какой бы то ни было математической задачи, была чужда как древним египтянам, так и древним вавилонянам. Только с Пифагора начинается становление математики как дедуктивной науки, и одним из первых шагов на этом пути было решение задачи о пифагоровых тройках. Первые решения уравнения (а2+b2=c2) античная традиция связывает с именами Пифагора и Платона.
Слайд 16
“Геометрия владеет двумя сокровищами: одно из них - это теорема Пифагора,
а другое - деление отрезка в среднем и крайнем отношении… Первое можно сравнить с мерой золота; второе же больше напоминает драгоценный камень”.
Иоганн Кеплер
Иоганн Кеплер