- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по внеурочной деятельности по математике Золотое сечение
Содержание
- 1. Презентация по внеурочной деятельности по математике Золотое сечение
- 2. « Геометрия владеет двумя сокровищами: одно из
- 3. ЕВКЛИД (III век до н.э.) ПИФАГОР (VI век до н.э.)
- 4. Античный циркуль золотого сечения
- 5. Леонардо да Винчи Лука Пачоли
- 6. Леонардо из Пизы,Леонардо Фибоначчи( сын Боначчи )
- 7. Ряд чисел Фибоначчи 1, 1, 2, 3,
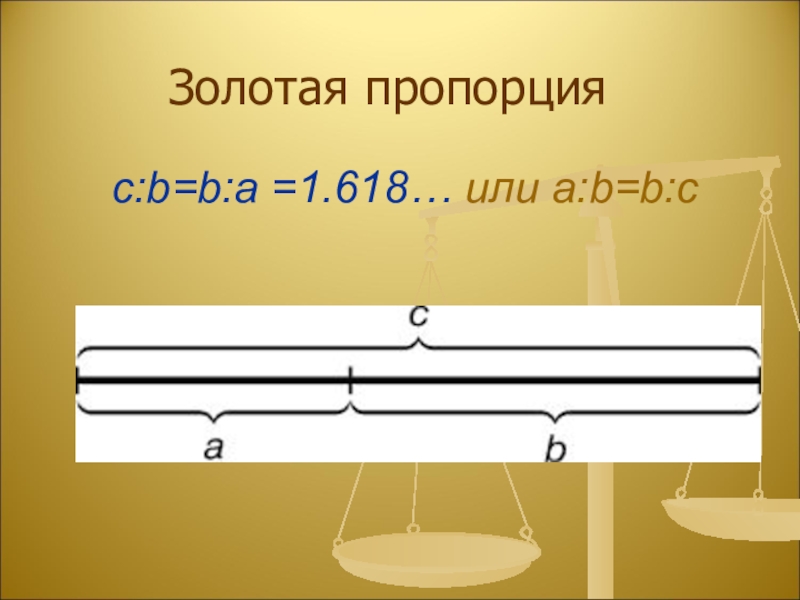
- 8. с:b=b:a =1.618… или a:b=b:сЗолотая пропорция
- 9. Деление отрезка в золотом отношенииАBC
- 10. Построение золотого прямоугольникаАВСДАВВС1,618
- 11. Из «золотых»треугольников состоит «орел»
- 12. В правильной пятиконечной звезде каждый сегмент делится
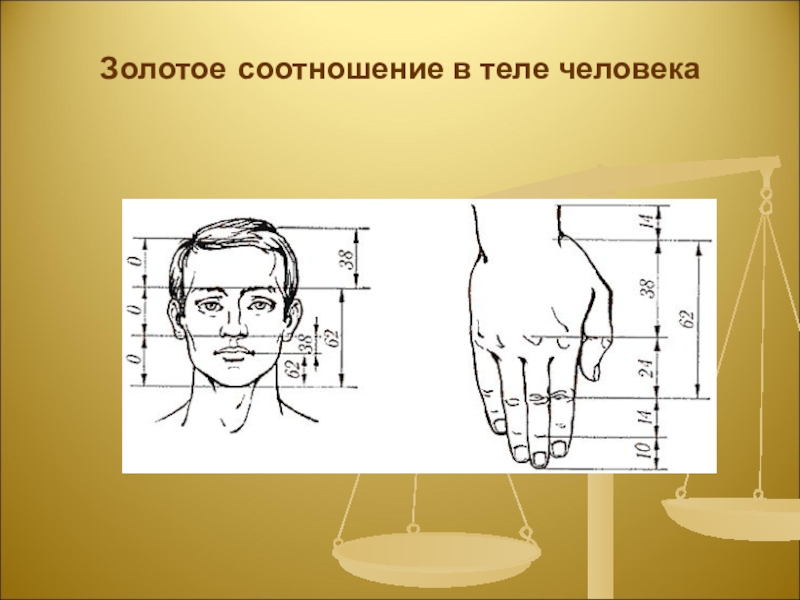
- 13. Золотое соотношение в теле человека
- 14. Спираль Архимеда
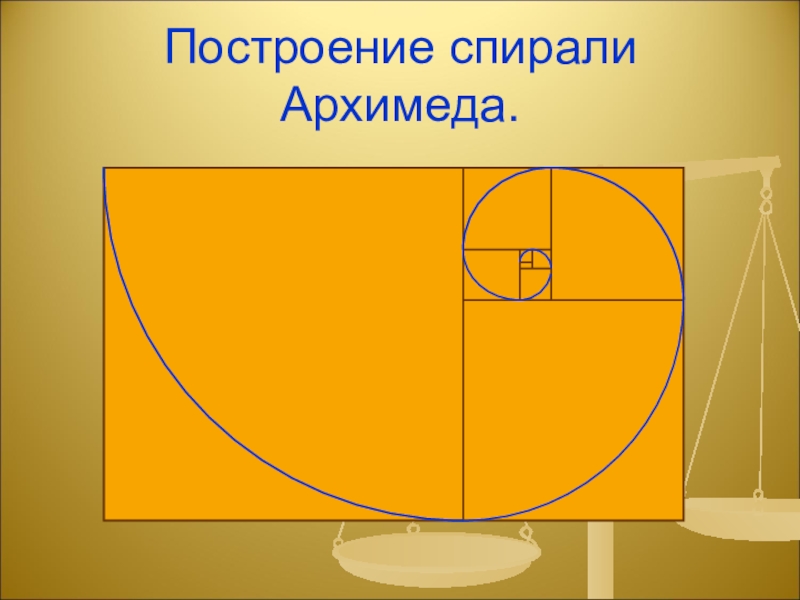
- 15. Построение спирали Архимеда.
- 16. "Золотые" спирали широко распространены в биологическом мире.
- 17. Слайд 17
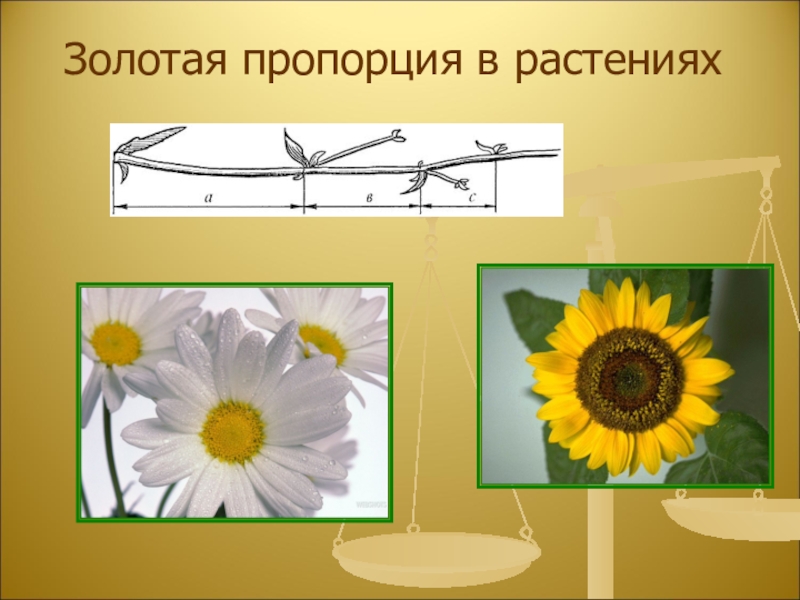
- 18. Золотая пропорция в растениях
- 19. Золотое отношение в животном мире
- 20. Музей Гармониии Золотого Сечения
« Геометрия владеет двумя сокровищами: одно из них- это теорема Пифагора, а другое – деление отрезка в среднем и крайнем отношении… Первое можно сравнить с мерой золота; второе же больше напоминает драгоценный камень.»
Слайд 2« Геометрия владеет двумя сокровищами: одно из них- это теорема Пифагора,
а другое – деление отрезка в среднем и крайнем отношении… Первое можно сравнить с мерой золота; второе же больше напоминает драгоценный камень.»
Иоганн Кеплер
Иоганн Кеплер
Слайд 7Ряд чисел Фибоначчи
1, 1, 2, 3, 5, 8, 13, 21,
34, 55 , 89, 144, 233, 377, 610, 987, 1 597, 2 584, 4181 и т.д.
- Каждое следующее число, начиная с третьего равно сумме предыдущих двух.
- Если какой-либо член последовательности Фибоначчи разделить на предшествующий ему (например, 13:8), результатом будет величина, колеблющаяся около иррационального значения 1,61803398875... ,то есть отношение равно золотой пропорции.
- Каждое следующее число, начиная с третьего равно сумме предыдущих двух.
- Если какой-либо член последовательности Фибоначчи разделить на предшествующий ему (например, 13:8), результатом будет величина, колеблющаяся около иррационального значения 1,61803398875... ,то есть отношение равно золотой пропорции.
Слайд 11 Из «золотых»треугольников состоит «орел»
5-конечной звезды, которую общество
пифагорейцев избрало своим символом. Такая звезда называется «Звёздчатым пятиугольником.»
Отношение M/m равно числу Ф
«Золотой»пятиугольник
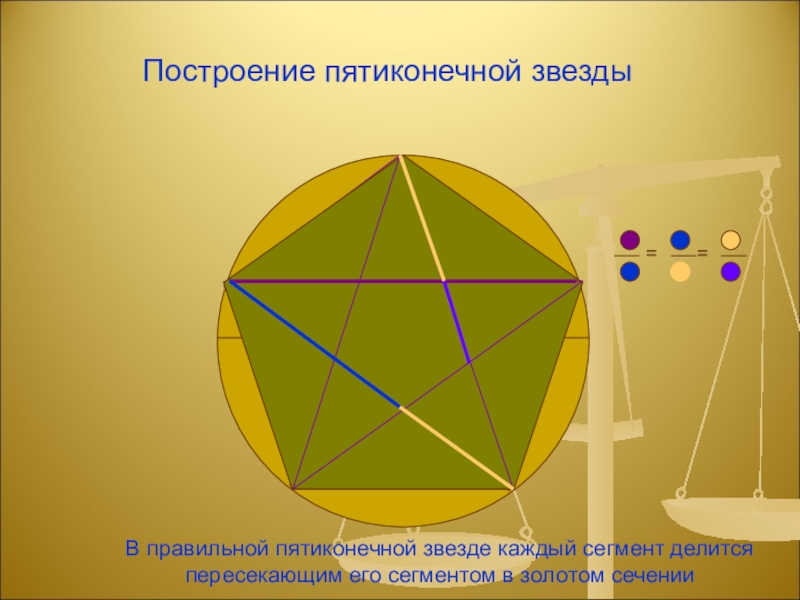
Слайд 12В правильной пятиконечной звезде каждый сегмент делится пересекающим его сегментом в
золотом сечении
Построение пятиконечной звезды
= =