Брянска
Ивашкин Даниил
Учитель математики: Тимофеева О.Л.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по теме Треугольники (8 класс)
Содержание
- 1. Презентация по теме Треугольники (8 класс)
- 2. Треугольник – это геометрическая фигура, которая состоит
- 3. Свойства углов треугольникаСумма углов треугольника равна 180˚.У
- 4. Соотношение между сторонами и углами треугольникаВ треугольнике:
- 5. Треугольник называется прямоугольным, если у него есть
- 6. Виды треугольниковТреугольник называется равнобедренным, если у него
- 7. Периметр треугольникаСумма длин трёх сторон треугольника называется
- 8. Биссектриса треугольника — это отрезок луча, исходящего
- 9. Медиана треугольника — это отрезок, соединяющий вершину
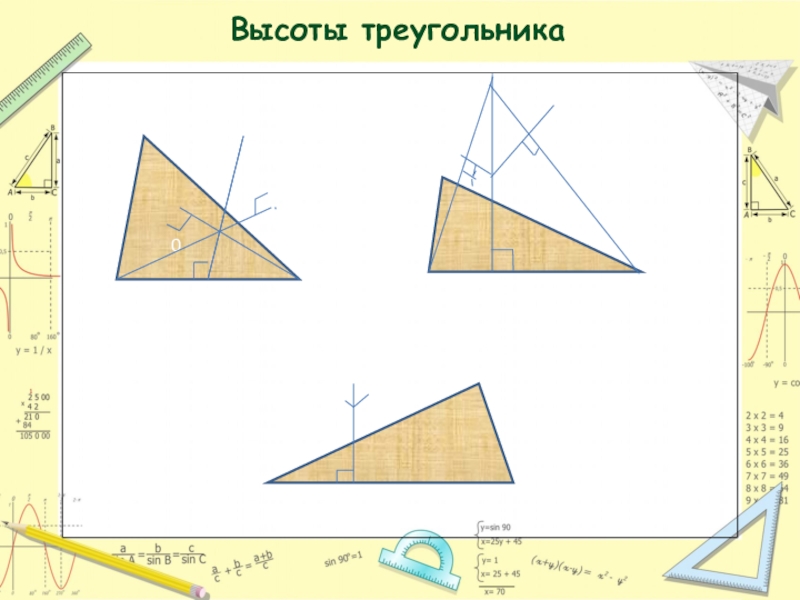
- 10. Высотой треугольника называется перпендикуляр, проведенный из вершины
- 11. Высоты треугольника0
- 12. Прямую, проходящую через середину отрезка перпендикулярно к
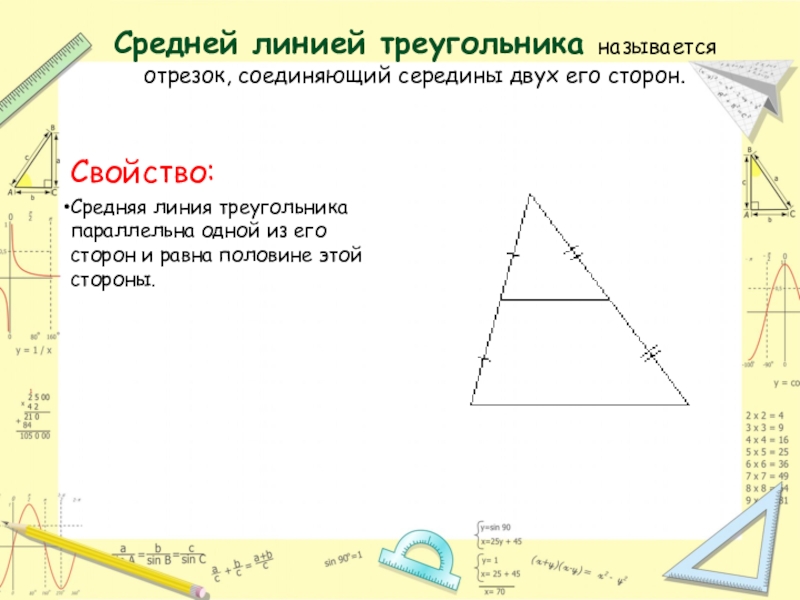
- 13. Средней линией треугольника называется отрезок, соединяющий середины
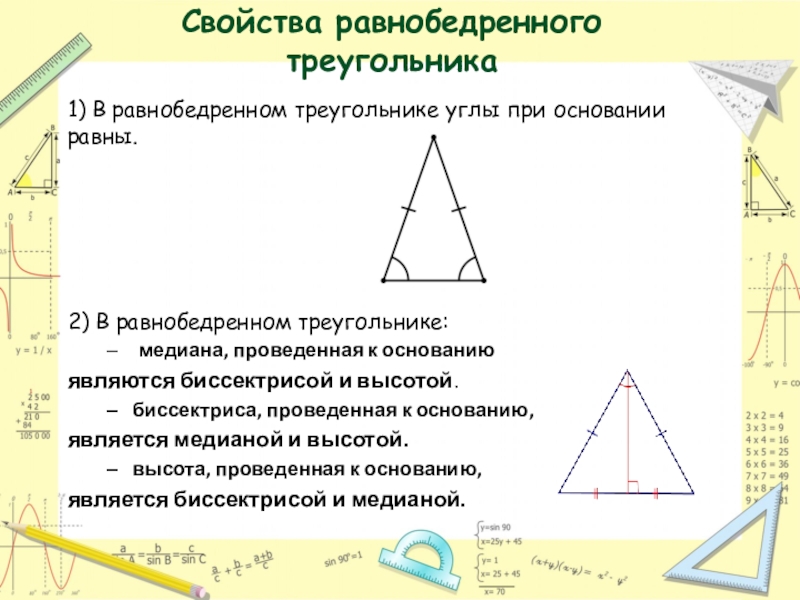
- 14. Свойства равнобедренного треугольника1) В равнобедренном треугольнике углы
- 15. Свойства прямоугольного треугольникаСумма двух острых углов прямоугольного
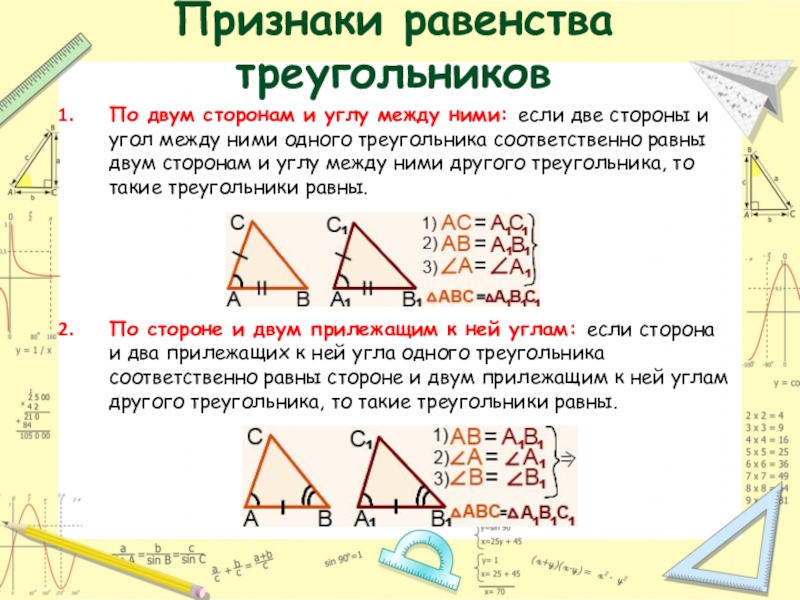
- 16. Признаки равенства треугольниковПо двум сторонам и углу
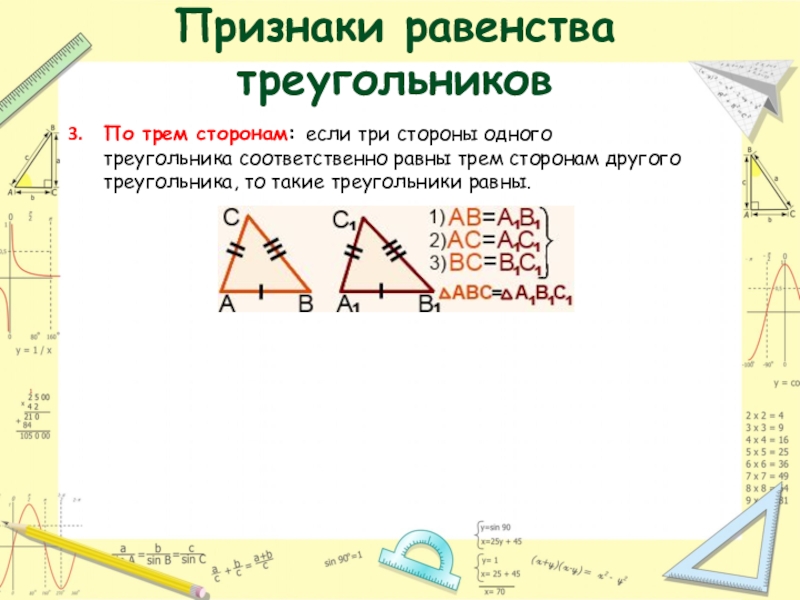
- 17. Признаки равенства треугольниковПо трем сторонам: если три
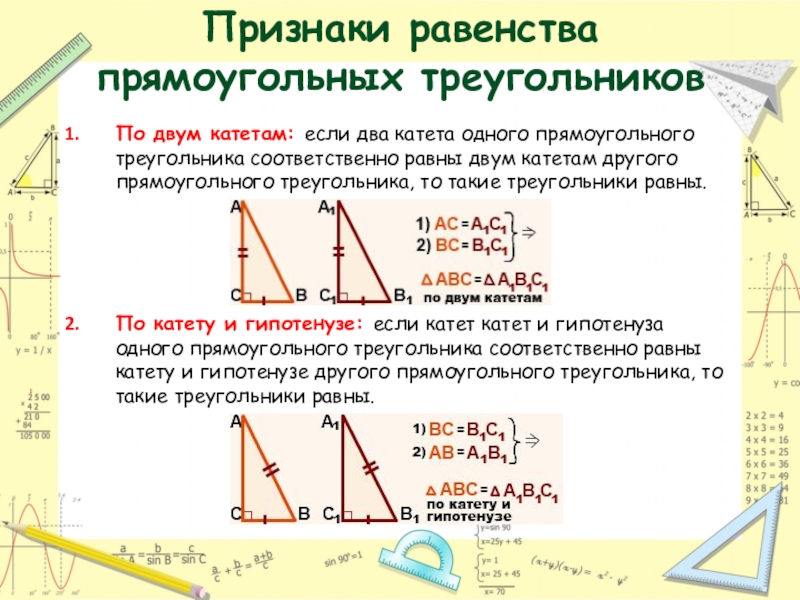
- 18. Признаки равенства прямоугольных треугольниковПо двум катетам: если
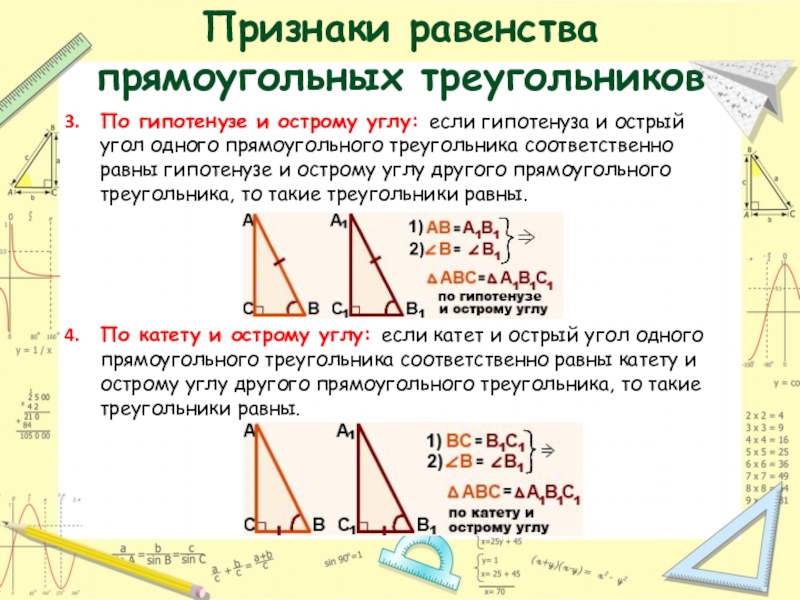
- 19. Признаки равенства прямоугольных треугольниковПо гипотенузе и острому
Треугольник – это геометрическая фигура, которая состоит из трёх точек, не лежащих на одной прямой (вершин треугольника) и трёх отрезков с концами в этих точках (сторон треугольника).
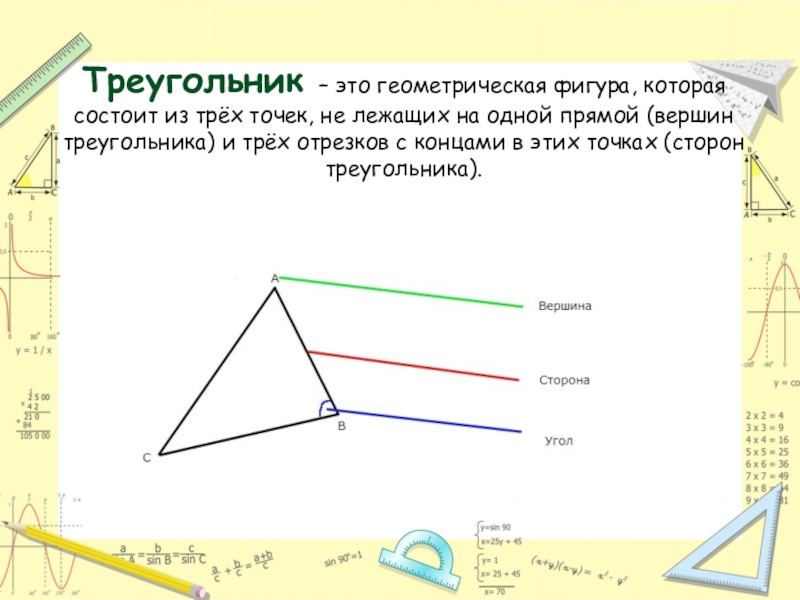
Слайд 2Треугольник – это геометрическая фигура, которая состоит из трёх точек, не
лежащих на одной прямой (вершин треугольника) и трёх отрезков с концами в этих точках (сторон треугольника).
Слайд 3Свойства углов треугольника
Сумма углов треугольника равна 180˚.
У любого треугольника хотя бы
два угла острые.
Внешний угол треугольника равен сумме двух внутренних, не смежных с ним.
Внешний угол треугольника равен сумме двух внутренних, не смежных с ним.
Слайд 4Соотношение между сторонами и углами треугольника
В треугольнике: 1) против большей стороны
лежит больший угол;
2) против большего угла лежит большая сторона.
Неравенство треугольника: 1)каждая сторона треугольника меньше суммы двух других сторон;
2) в прямоугольном треугольнике гипотенуза больше катета;
3)для любых трёх точек А, В и С, не лежащих на одной прямой, справедливы неравенства: АВ < АС + ВС,
АС < АВ + ВС,
ВС < ВА + АС.
2) против большего угла лежит большая сторона.
Неравенство треугольника: 1)каждая сторона треугольника меньше суммы двух других сторон;
2) в прямоугольном треугольнике гипотенуза больше катета;
3)для любых трёх точек А, В и С, не лежащих на одной прямой, справедливы неравенства: АВ < АС + ВС,
АС < АВ + ВС,
ВС < ВА + АС.
Слайд 5
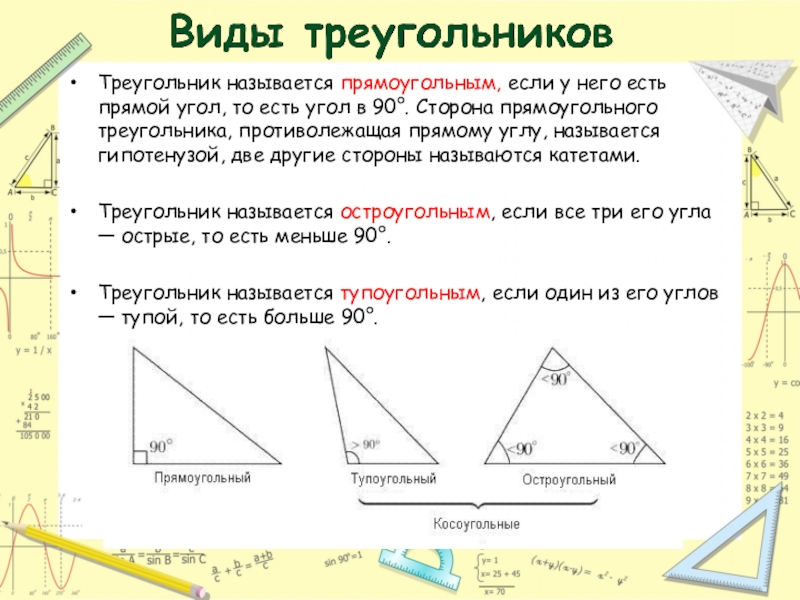
Треугольник называется прямоугольным, если у него есть прямой угол, то есть
угол в 90°. Сторона прямоугольного треугольника, противолежащая прямому углу, называется гипотенузой, две другие стороны называются катетами.
Треугольник называется остроугольным, если все три его угла — острые, то есть меньше 90°.
Треугольник называется тупоугольным, если один из его углов — тупой, то есть больше 90°.
Треугольник называется остроугольным, если все три его угла — острые, то есть меньше 90°.
Треугольник называется тупоугольным, если один из его углов — тупой, то есть больше 90°.
Слайд 6Виды треугольников
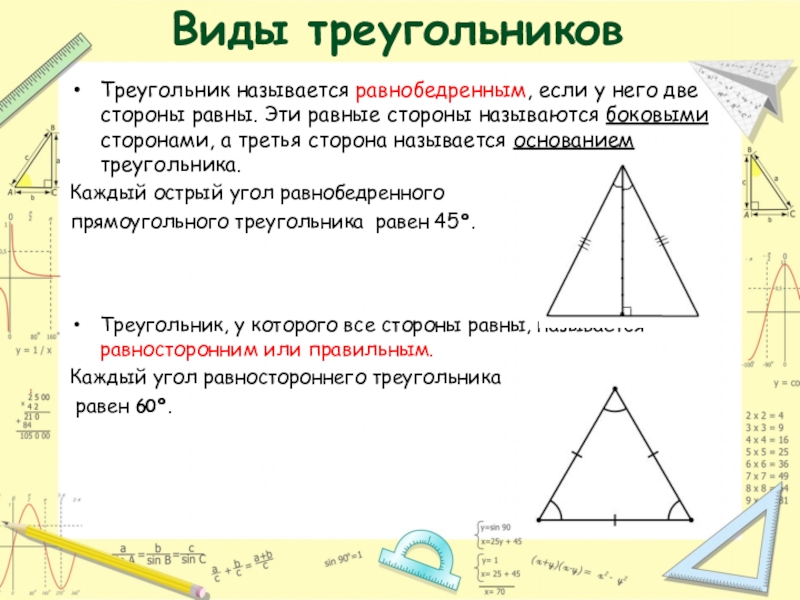
Треугольник называется равнобедренным, если у него две стороны равны. Эти
равные стороны называются боковыми сторонами, а третья сторона называется основанием треугольника.
Каждый острый угол равнобедренного
прямоугольного треугольника равен 45º.
Треугольник, у которого все стороны равны, называется равносторонним или правильным.
Каждый угол равностороннего треугольника
равен 60º.
Каждый острый угол равнобедренного
прямоугольного треугольника равен 45º.
Треугольник, у которого все стороны равны, называется равносторонним или правильным.
Каждый угол равностороннего треугольника
равен 60º.
Слайд 7Периметр треугольника
Сумма длин трёх сторон треугольника называется его периметром.
Для разностороннего
треугольника:
Р = АВ+АС+ВС
2. Для равнобедренного треугольника:
Р = 2АВ+АС, где АС – основание
Для равностороннего треугольника:
Р = 3АВ.
Р = АВ+АС+ВС
2. Для равнобедренного треугольника:
Р = 2АВ+АС, где АС – основание
Для равностороннего треугольника:
Р = 3АВ.
Слайд 8Биссектриса треугольника — это отрезок луча, исходящего из вершины треугольника к
противоположной стороне и делящий угол пополам
ЭЛЕМЕНТЫ ТРЕУГОЛЬНИКА
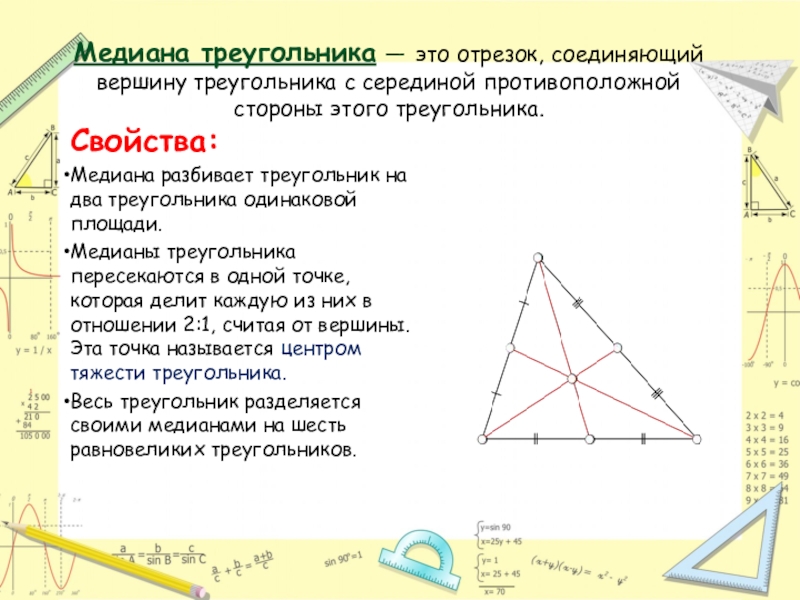
Слайд 9Медиана треугольника — это отрезок, соединяющий вершину треугольника с серединой противоположной
стороны этого треугольника.
Свойства:
Медиана разбивает треугольник на два треугольника одинаковой площади.
Медианы треугольника пересекаются в одной точке, которая делит каждую из них в отношении 2:1, считая от вершины. Эта точка называется центром тяжести треугольника.
Весь треугольник разделяется своими медианами на шесть равновеликих треугольников.
Слайд 10Высотой треугольника называется перпендикуляр, проведенный из вершины треугольника к прямой, содержащей
противоположную сторону этого треугольника.
Свойства:
В прямоугольном треугольнике высота, проведенная из вершины прямого угла, разбивает его на два треугольника, подобные исходному.
В остроугольном треугольнике две его высоты отсекают от него подобные треугольники.
Слайд 12Прямую, проходящую через середину отрезка перпендикулярно к нему, называют серединным перпендикуляром
к отрезку.
Свойства:
Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка. Верно и обратное утверждение: каждая точка, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к нему.
Точка пересечения серединных перпендикуляров, проведенных к сторонам треугольника, является центром окружности, описанной около этого треугольника.
Слайд 13Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.
Свойство:
Средняя линия
треугольника параллельна одной из его сторон и равна половине этой стороны.
Слайд 14Свойства равнобедренного треугольника
1) В равнобедренном треугольнике углы при основании равны.
2) В
равнобедренном треугольнике:
медиана, проведенная к основанию
являются биссектрисой и высотой.
биссектриса, проведенная к основанию,
является медианой и высотой.
высота, проведенная к основанию,
является биссектрисой и медианой.
медиана, проведенная к основанию
являются биссектрисой и высотой.
биссектриса, проведенная к основанию,
является медианой и высотой.
высота, проведенная к основанию,
является биссектрисой и медианой.
Слайд 15Свойства прямоугольного треугольника
Сумма двух острых углов прямоугольного треугольника равна 90º
Катет прямоугольного
треугольника, лежащий против угла в 30º, равен половине гипотенузы.
Слайд 16Признаки равенства треугольников
По двум сторонам и углу между ними: если две
стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
По стороне и двум прилежащим к ней углам: если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
По стороне и двум прилежащим к ней углам: если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
Слайд 17Признаки равенства треугольников
По трем сторонам: если три стороны одного
треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
Слайд 18Признаки равенства прямоугольных треугольников
По двум катетам: если два катета одного прямоугольного
треугольника соответственно равны двум катетам другого прямоугольного треугольника, то такие треугольники равны.
По катету и гипотенузе: если катет катет и гипотенуза одного прямоугольного треугольника соответственно равны катету и гипотенузе другого прямоугольного треугольника, то такие треугольники равны.
По катету и гипотенузе: если катет катет и гипотенуза одного прямоугольного треугольника соответственно равны катету и гипотенузе другого прямоугольного треугольника, то такие треугольники равны.
Слайд 19Признаки равенства прямоугольных треугольников
По гипотенузе и острому углу: если гипотенуза и
острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны.
По катету и острому углу: если катет и острый угол одного прямоугольного треугольника соответственно равны катету и острому углу другого прямоугольного треугольника, то такие треугольники равны.
По катету и острому углу: если катет и острый угол одного прямоугольного треугольника соответственно равны катету и острому углу другого прямоугольного треугольника, то такие треугольники равны.
