- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по теме сумма углов треугольника
Содержание
- 1. Презентация по теме сумма углов треугольника
- 2. Сумма углов треугольника равна 180 0.
- 3. Дано: ∆ АВСДоказать: ∠А +∠В +∠С =
- 4. Доказательство № 2 из учебника А.П.Киселева 1961
- 5. АВС1. Продолжим сторону АС.DПроведем СЕ ⎢⎢АВ.Е2. ∠А
- 6. В некоторых школах нашей страны геометрию изучают
- 7. Дано: ∆ АВСДоказать: ∠А +∠В +∠С =
- 8. Следствия из теоремы о сумме углов треугольника1.
- 9. Слайд 9
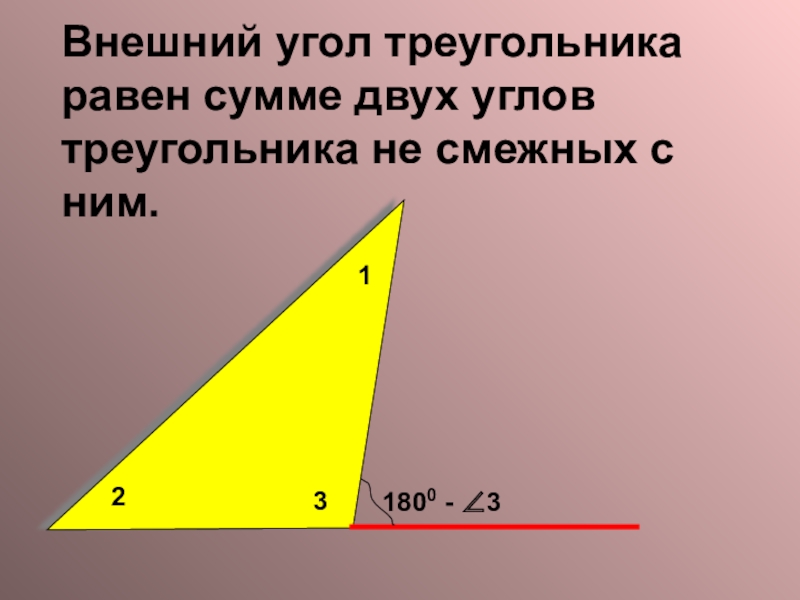
- 10. 1800 - ∠3321Внешний угол треугольника равен сумме двух углов треугольника не смежных с ним.
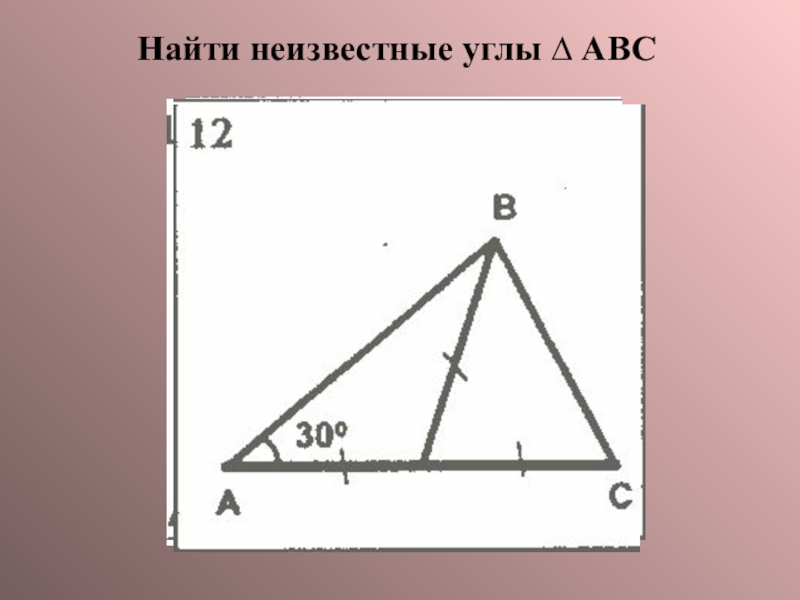
- 11. Найти неизвестные углы ∆ АВС
- 12. Домашнее задание: п.п.30 – 31, вопросы 1
- 13. Свойства прямоугольных треугольников1. Сумма острых углов прямоугольного треугольника равна 900.αβ=900-α
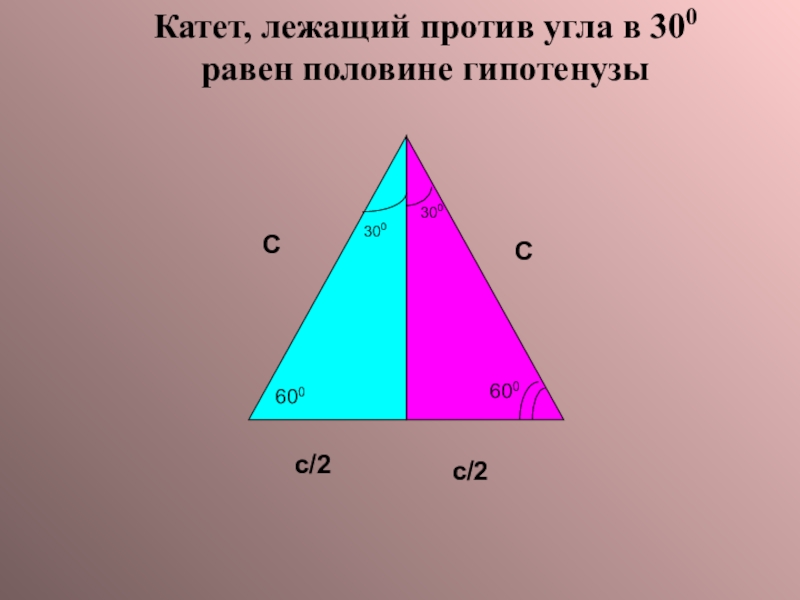
- 14. С300с/2600с/2С600Катет, лежащий против угла в 300 равен половине гипотенузы300
Слайд 3Дано: ∆ АВС
Доказать: ∠А +∠В +∠С = 1800
Доказательство:
2. ∠1 и ∠4
3. ∠3 и ∠5 – накрест лежащие при параллельных а и АС и секущей ВС.
1. Проведем через вершину В прямую а ⎢⎢АС.
4. Поэтому ∠4 = ∠1, ∠5 = ∠3. (1)
5. Очевидно, ∠4+∠2+∠5=1800.
6. Учитывая равенства (1), получаем
∠1+∠2 +∠3 = 1800, или ∠А +∠В +∠С = 1800.
Ч.т.д.
А
С
В
а
1
4
3
5
2
Слайд 4Доказательство № 2 из учебника А.П.Киселева 1961 год
А так эта книга
В 2017 г. исполнится 165 лет со дня рождения А.П.Киселева.
Его "Элементарная геометрия"
вышла в 1892 г.
В наше время книги Киселева стали
библиографической редкостью .
Слайд 5
А
В
С
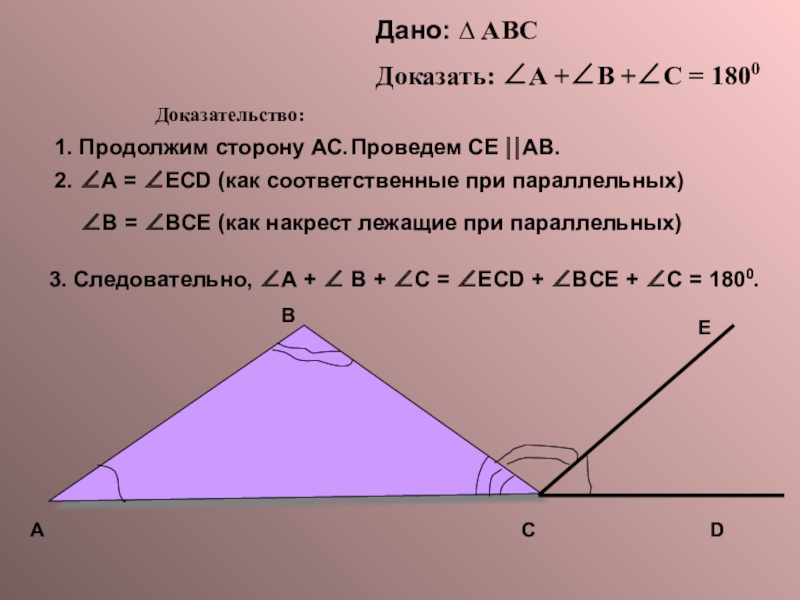
1. Продолжим сторону АС.
D
Проведем СЕ ⎢⎢АВ.
Е
2. ∠А = ∠ЕСD (как соответственные
∠В = ∠ВСЕ (как накрест лежащие при параллельных)
3. Следовательно, ∠А + ∠ В + ∠С = ∠ECD + ∠BCE + ∠C = 1800.
Дано: ∆ АВС
Доказать: ∠А +∠В +∠С = 1800
Доказательство:
Слайд 6В некоторых школах нашей страны геометрию изучают по учебнику А.В. Погорелова
В
еще одно
доказательство
теоремы о сумме углов
треугольника
Слайд 7
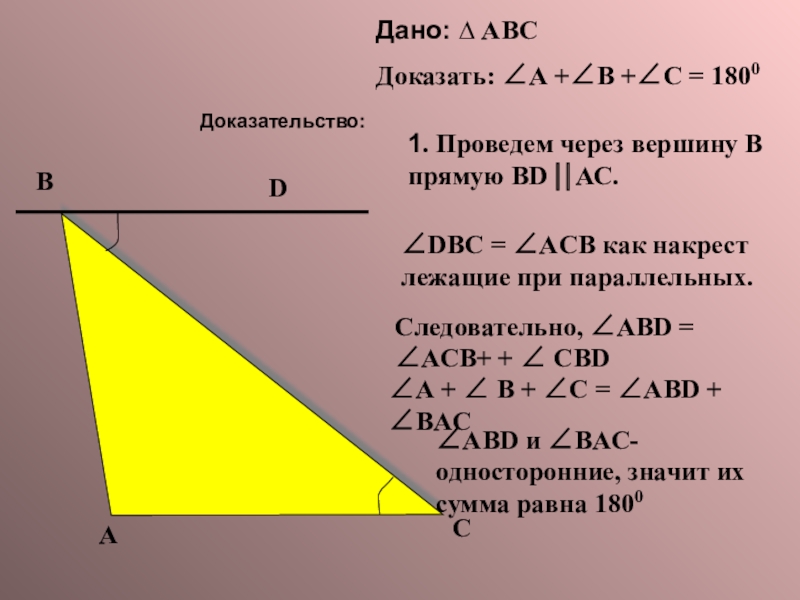
Дано: ∆ АВС
Доказать: ∠А +∠В +∠С = 1800
С
А
В
Доказательство:
1. Проведем через вершину
D
∠DBC = ∠ACB как накрест лежащие при параллельных.
Следовательно, ∠ABD = ∠АСВ+ + ∠ СВD
∠А + ∠ В + ∠С = ∠ABD + ∠BAC
∠ABD и ∠BAC- односторонние, значит их сумма равна 1800
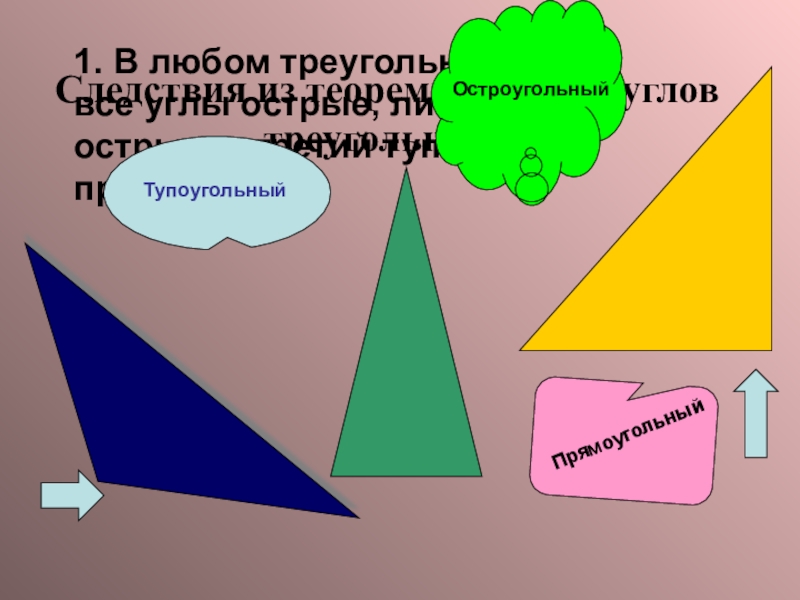
Слайд 8Следствия из теоремы о сумме углов треугольника
1. В любом треугольнике либо
Тупоугольный
Остроугольный
Прямоугольный