- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по теме: Решение задач на применение аксиом стереометрии и их следствий
Содержание
- 1. Презентация по теме: Решение задач на применение аксиом стереометрии и их следствий
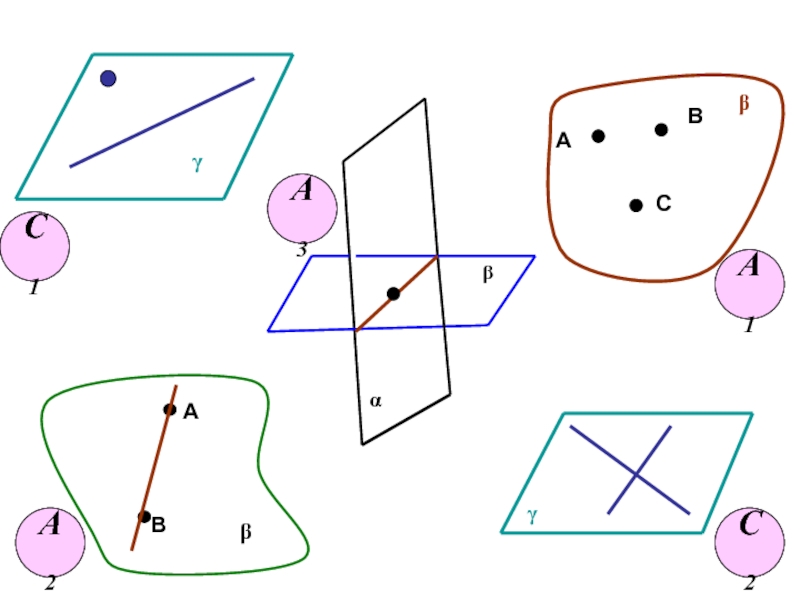
- 2. 12345А1А2А3С1С2
- 3. Дан куб АВСDA1B1C1D1.D1DС1СВ1ВА1АMТочка М лежит на ребре
- 4. Решение задач. №1.Дана треугольная призмаАВСА1В1С1. М
- 5. D1ВАDС1СВ1РА1Решение задач. №2.Дан куб АВСDА1В1С1D1Р принадлежит ВВ1.ВР
- 6. D1ВАDС1СВ1РА1Решение задач. №3.Дан куб АВСDА1В1С1D1Р принадлежит ВВ1.ВР
- 7. Домашнее задание: 1) Выполнить самостоятельную
- 8. Диктант.Необходимо ответить на вопросы:№1
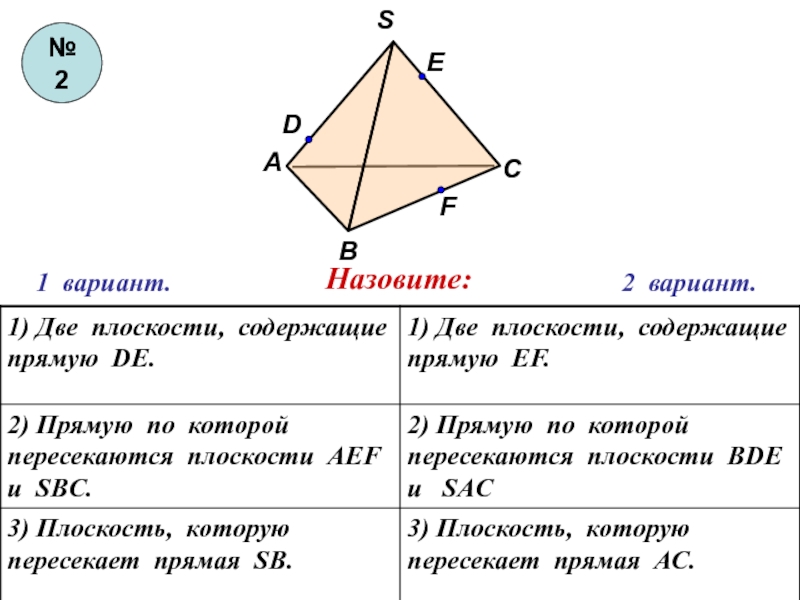
- 9. 1 вариант.2 вариант.Назовите:№2
12345А1А2А3С1С2
Слайд 3
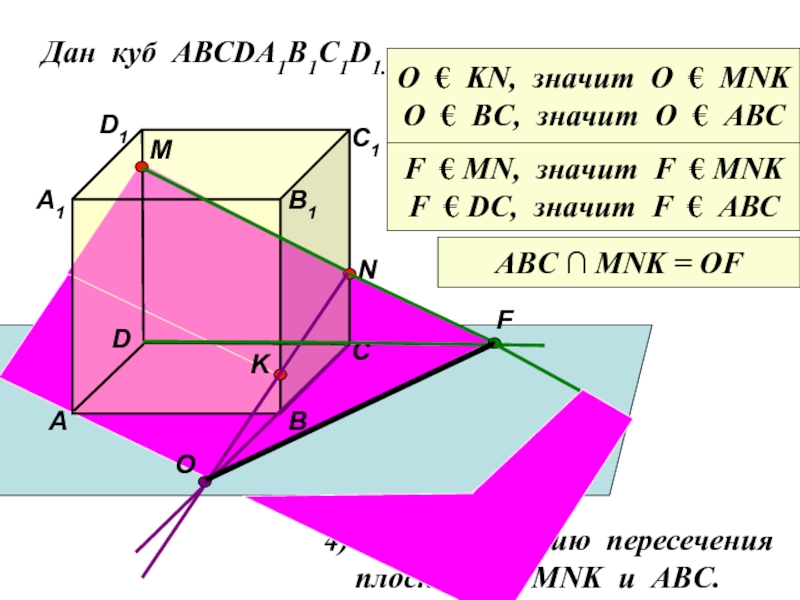
Дан куб АВСDA1B1C1D1.
D1
D
С1
С
В1
В
А1
А
M
Точка М лежит на
ребре DD1
N
Точка N лежит
на
ребре CC1
ребре CC1
K
Точка K лежит на
ребре BB1
O
F
4) Найдите линию пересечения
плоскостей MNK и ABC.
ABC ∩ MNK = OF
O € KN, значит О € МNK
O € ВC, значит О € АВС
F € MN, значит F € MNK
F € DC, значит F € АВС
Слайд 4
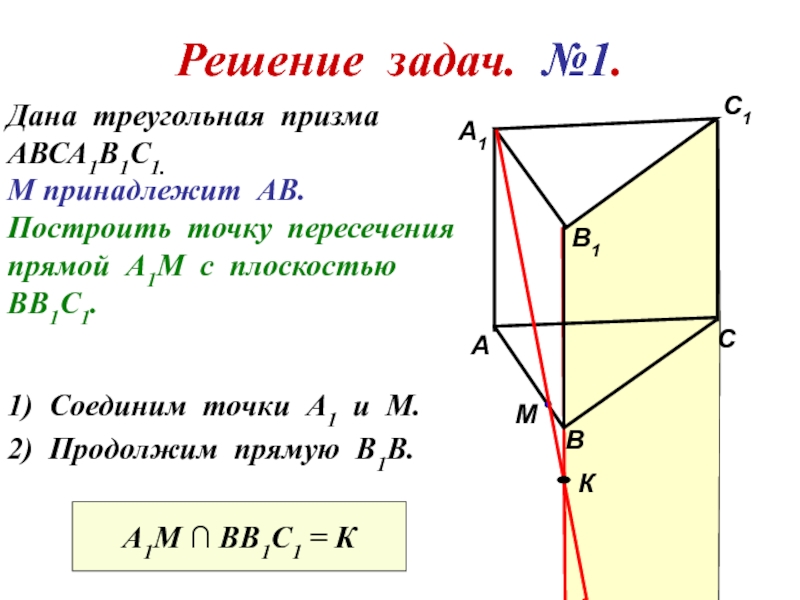
Решение задач. №1.
Дана треугольная призма
АВСА1В1С1.
М принадлежит АВ.
Построить точку пересечения
прямой
А1М с плоскостью
ВВ1С1.
ВВ1С1.
А
В
С1
С
В1
А1
М
1) Соединим точки А1 и М.
2) Продолжим прямую В1В.
К
А1М ∩ ВВ1С1 = К
Слайд 5
D1
В
А
D
С1
С
В1
Р
А1
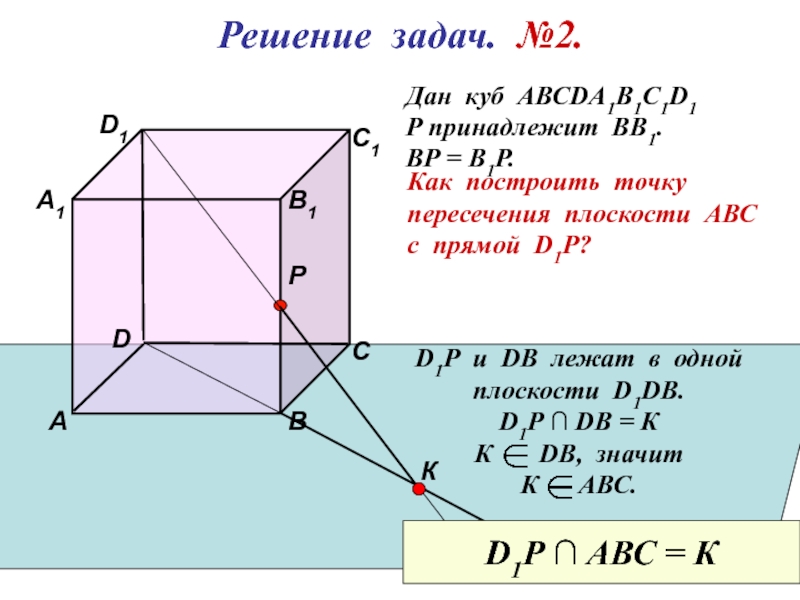
Решение задач. №2.
Дан куб АВСDА1В1С1D1
Р принадлежит ВВ1.
ВР = В1Р.
Как построить точку
пересечения плоскости АВС
с прямой D1P?
К
D1Р u DB лежат в одной
плоскости D1DB.
D1P ∩ DB = К
К DB, значит
К АВС.
D1P ∩ АВС = К
Слайд 6D1
В
А
D
С1
С
В1
Р
А1
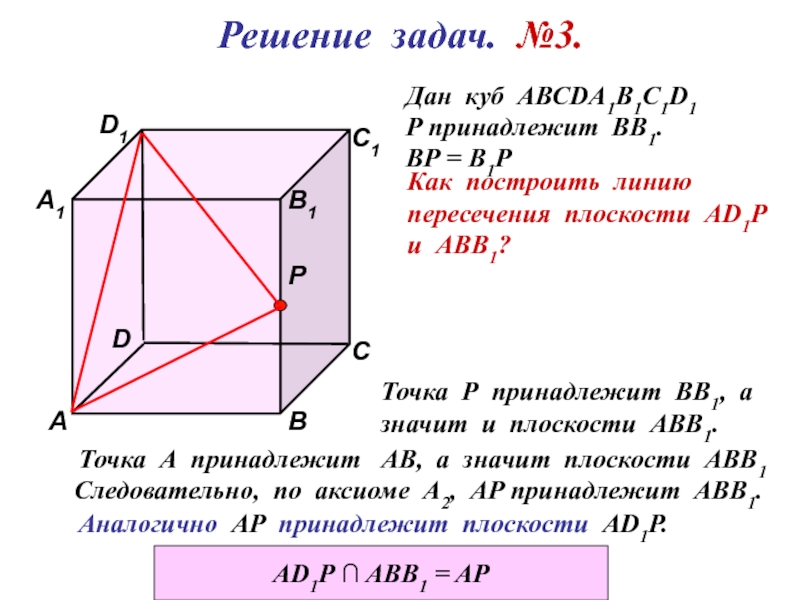
Решение задач. №3.
Дан куб АВСDА1В1С1D1
Р принадлежит ВВ1.
ВР = В1Р
Как построить линию
пересечения плоскости АD1Р
и АВВ1?
Точка Р принадлежит ВВ1, а
значит и плоскости АВВ1.
Точка А принадлежит АВ, а значит плоскости АВВ1
Следовательно, по аксиоме А2, АР принадлежит АВВ1.
Аналогично АР принадлежит плоскости АD1P.
АD1P ∩ ABB1 = AP
Слайд 7Домашнее задание:
1) Выполнить самостоятельную
работу в рабочей
тетради
на стр. 11 задания 1 – 4;
На стр. 17 – 18 №№ 1; 2; 3.
на стр. 11 задания 1 – 4;
На стр. 17 – 18 №№ 1; 2; 3.
Желаю успехов!
