- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по теме: Преобразование подобия (11 класс)
Содержание
- 1. Презентация по теме: Преобразование подобия (11 класс)
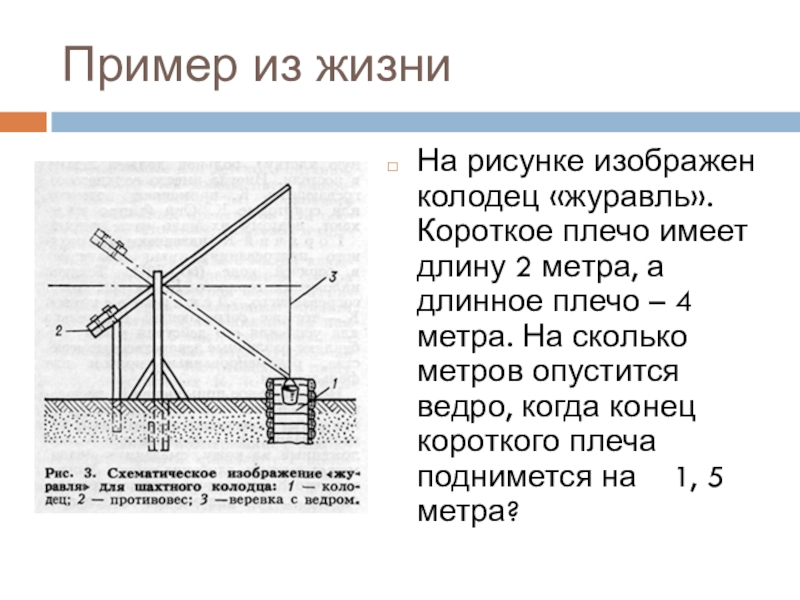
- 2. Пример из жизниНа рисунке изображен колодец «журавль».
- 3. Разделы Преобразование подобияПодобные фигуры и их свойстваПризнак
- 4. Преобразование подобияПреобразование одной фигуры в другую называется
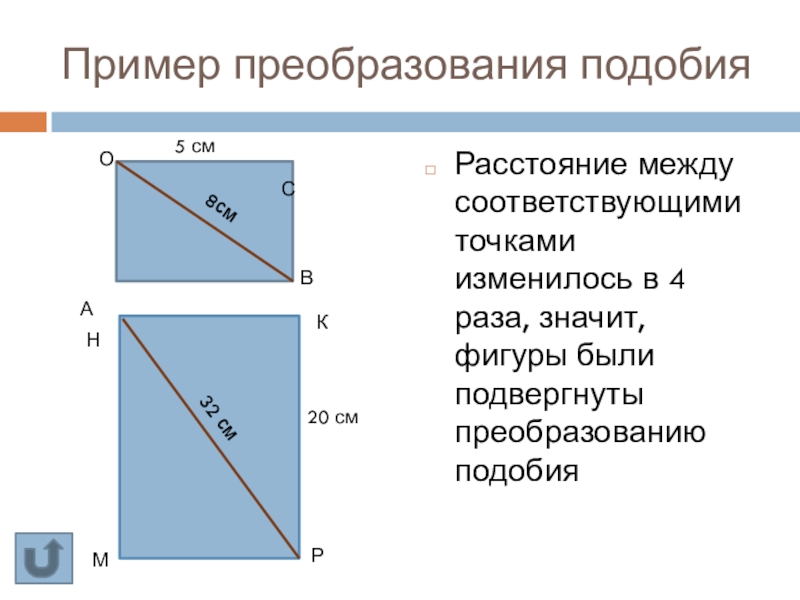
- 5. Пример преобразования подобияРасстояние между соответствующими точками изменилось
- 6. Свойства преобразования подобия Свойство 1:Преобразование подобия
- 7. Задание 1Квадрат F1 был подвергнут некоторому преобразованию.
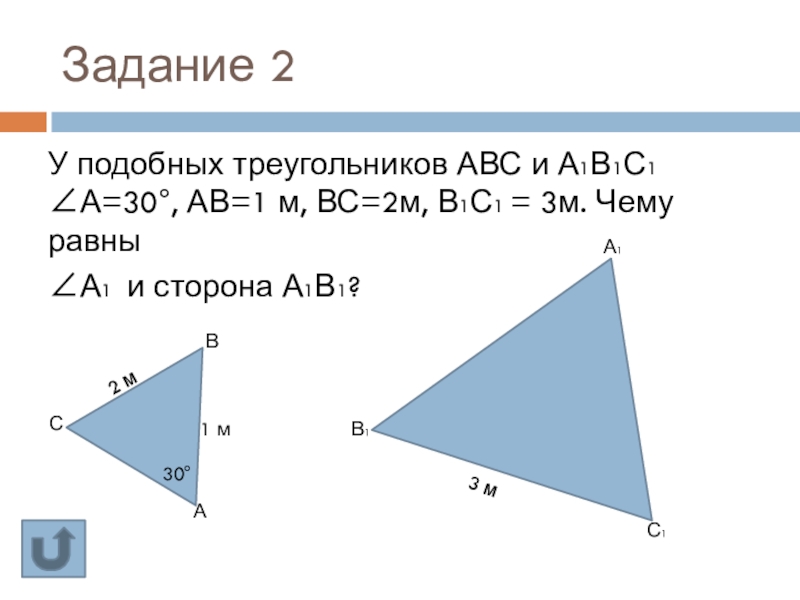
- 8. Задание 2У подобных треугольников АВС и А1В1С1
- 9. Проверь себяЧто такое преобразование подобия?Какие свойства преобразования подобия ты знаешь?Что такое коэффициент подобия?
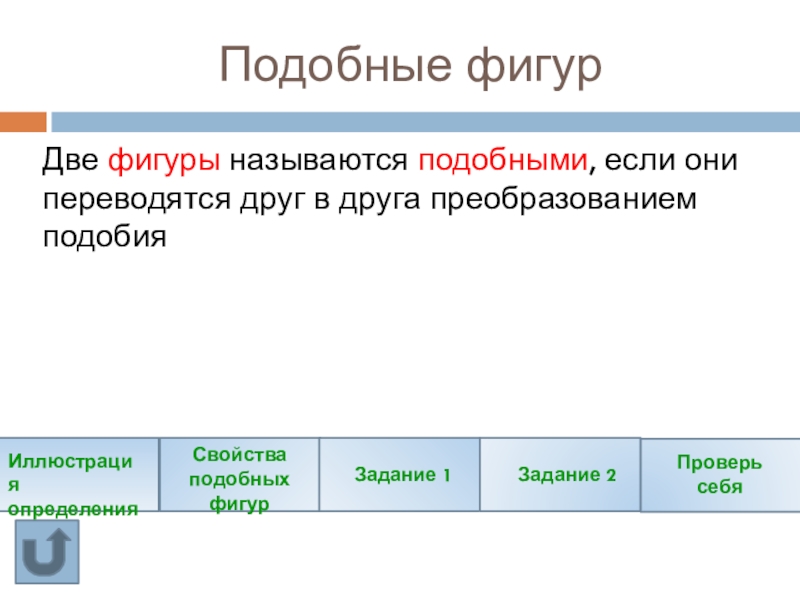
- 10. Подобные фигурДве фигуры называются подобными, если они
- 11. Подобные фигурыРасстояние между соответствующими точками изменилось в
- 12. Свойства подобных фигурЕсли фигура А подобна фигуре
- 13. Пример 1Квадрат А ∾ квадрату В, а
- 14. Пример 2 ∆АВС ∾
- 15. Задание 1Дано: ∆АРЕ ∾ ∆НРО Определите:
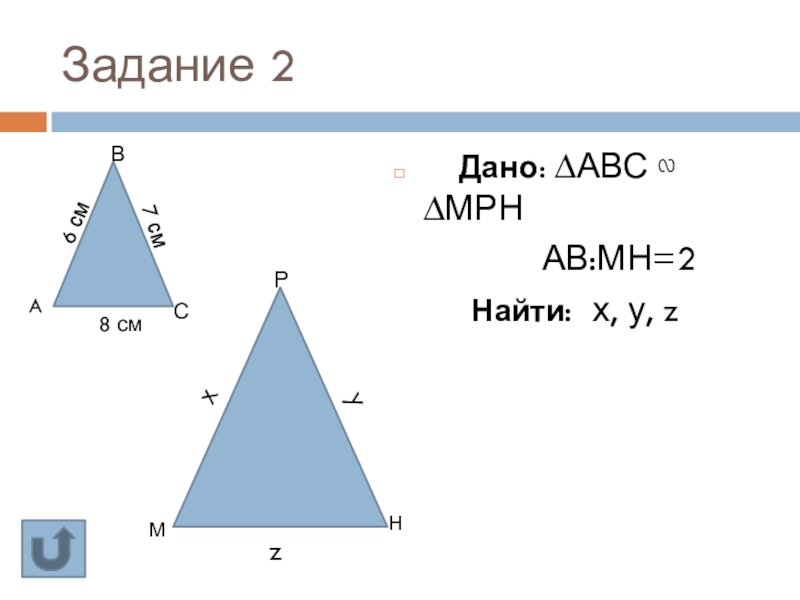
- 16. Задание 2 Дано: ∆АВС ∾ ∆МРН
- 17. Проверь себяКакие фигуры называются подобными?Каким знаком обозначается подобие фигур?Как записывается подобие треугольников?
- 18. Признак подобия треугольников по двум углам(
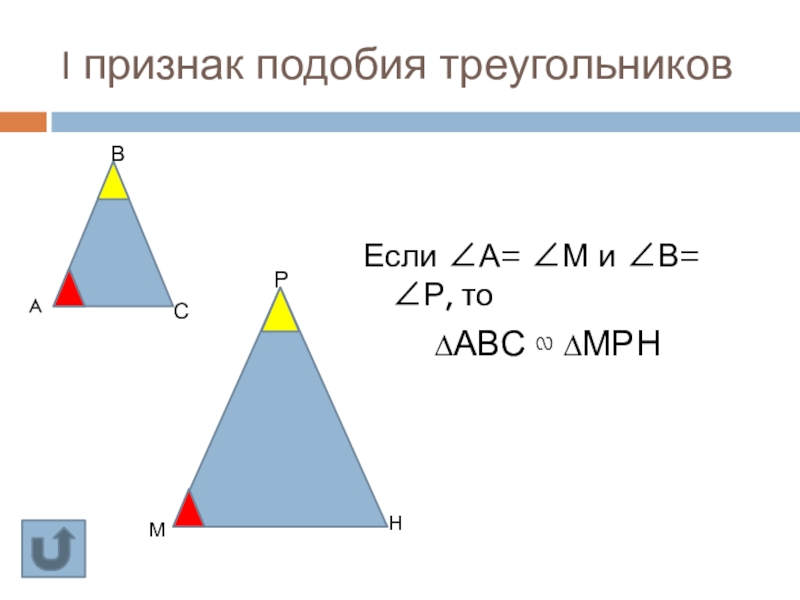
- 19. I признак подобия треугольников Если ∠А= ∠М
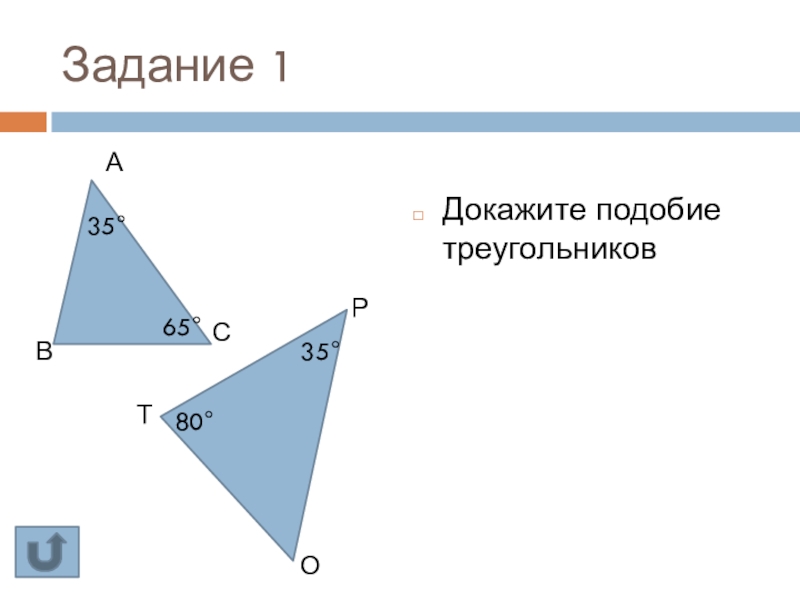
- 20. Задание 1Докажите подобие треугольниковАСВОРТ35°65°35°80°
- 21. Задание 2Докажите подобие треугольников и запишите равенство отношений соответствующих сторон.АРТСЕ
- 22. Задание 3Дано: АМРТ - трапеция МО=4см,
- 23. Проверь себяКакие условия должны выполняться для подобия
- 24. Признак подобия треугольников по двум сторонам и
- 25. II признак подобия треугольниковЕсли ∠В= ∠В1 и
- 26. Задание 1 А В
- 27. Задание 2 А В
- 28. Задание 3Дано: АО=2 см, ОС=5см, ЕО=4см, МО=10 см, АС=6 см Найти: длину МЕАОЕМС?
- 29. Проверь себя Перечисли условия для подобия треугольников
- 30. Признак подобия треугольников по трем сторонам (III
- 31. III признак подобия треугольниковЕсли ∆АВС ∾ ∆А1В1С1АВСС1В1А1
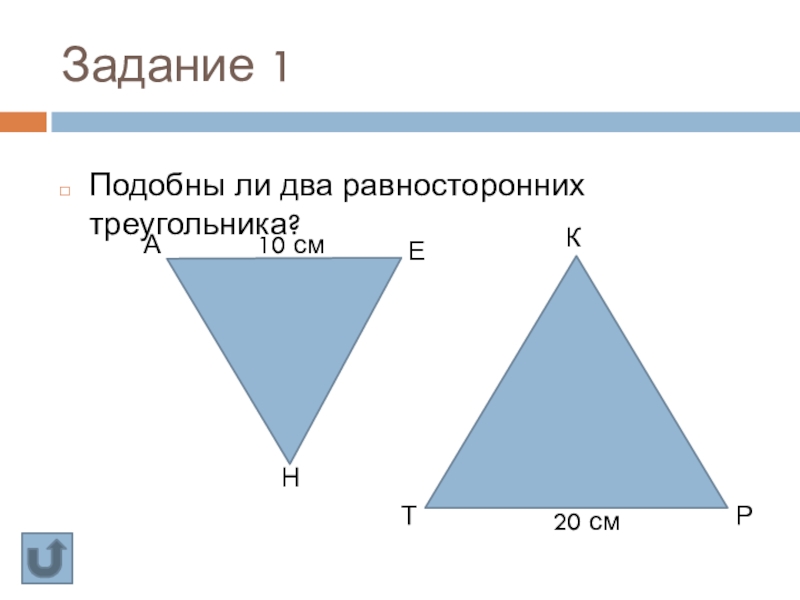
- 32. Задание 1Подобны ли два равносторонних треугольника?АНЕТРК10 см20 см
- 33. Задание 2Подобны ли треугольники АВС и МРК,
- 34. Задание 3Стороны треугольника равны 8 м, 16
- 35. Проверь себяСформулируй условие, при котором треугольники будут
- 36. Подобие прямоугольных треугольников Для подобия прямоугольных
- 37. Подобие прямоугольных треугольниковЕсли треугольники прямоугольные и
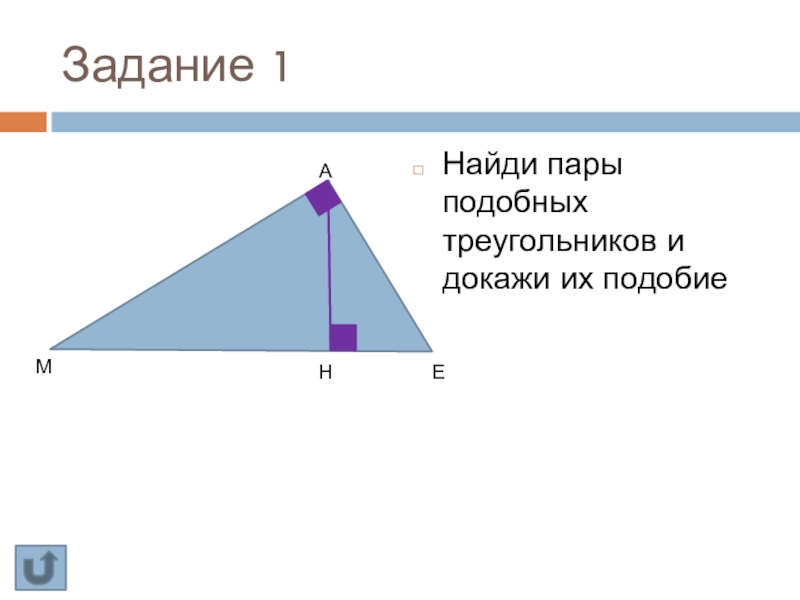
- 38. Задание 1Найди пары подобных треугольников и докажи их подобиеМЕАН
- 39. Задание 2В треугольнике МНК известны длины катетов
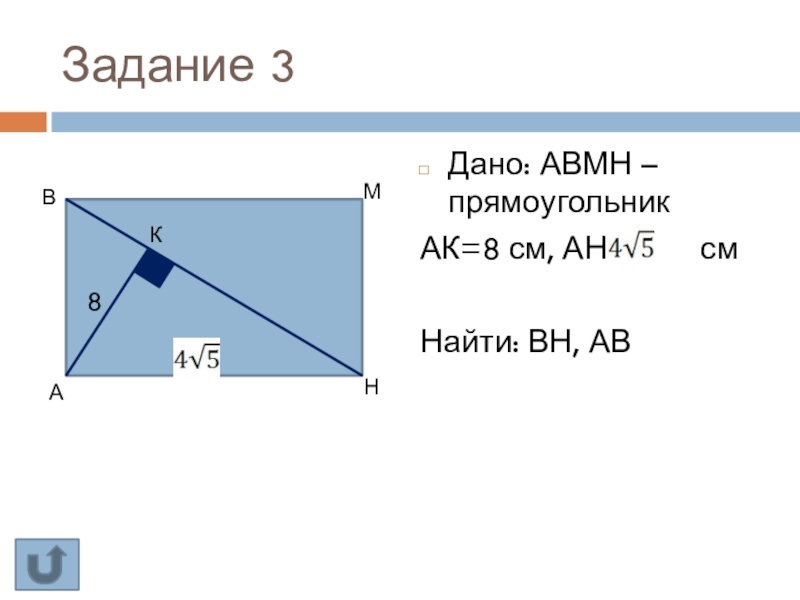
- 40. Задание 3Дано: АВМН – прямоугольникАК=8 см, АН= смНайти: ВН, АВАКНМВ8
- 41. Проверь себя Назовите условие, при котором прямоугольные
Пример из жизниНа рисунке изображен колодец «журавль». Короткое плечо имеет длину 2 метра, а длинное плечо – 4 метра. На сколько метров опустится ведро, когда конец короткого плеча поднимется на 1, 5 метра?
Слайд 2Пример из жизни
На рисунке изображен колодец «журавль». Короткое плечо имеет длину
2 метра, а длинное плечо – 4 метра. На сколько метров опустится ведро, когда конец короткого плеча поднимется на 1, 5 метра?
Слайд 3Разделы
Преобразование подобия
Подобные фигуры и их свойства
Признак подобия треугольников по двум
углам
Признак подобия треугольников по двум сторонам и углу между ними
Признак подобия треугольников по трем сторонам
Подобие прямоугольных треугольников
Признак подобия треугольников по двум сторонам и углу между ними
Признак подобия треугольников по трем сторонам
Подобие прямоугольных треугольников
Слайд 4Преобразование подобия
Преобразование одной фигуры в другую называется преобразованием подобия, если при
этом преобразовании расстояние между точками изменится в одно и то же число раз
Проверь себя
Свойства преобразования подобия
Задание 1
Задание 2
Иллюстрация определения
Слайд 5Пример преобразования подобия
Расстояние между соответствующими точками изменилось в 4 раза, значит,
фигуры были подвергнуты преобразованию подобия
А
Н
О
В
С
К
Р
М
8см
5 см
32 см
20 см
Слайд 6Свойства преобразования подобия
Свойство 1:
Преобразование подобия переводит прямые в прямые,
полупрямые в полупрямые, отрезки в отрезки;
Свойство 2:
Преобразование подобия сохраняет углы между полупрямыми
Свойство 2:
Преобразование подобия сохраняет углы между полупрямыми
Слайд 7Задание 1
Квадрат F1 был подвергнут некоторому преобразованию. В результате была получена
фигура F2. Будет ли данное преобразование являться преобразованием подобия? Свой ответ обоснуйте.
F1
F2
Слайд 8Задание 2
У подобных треугольников АВС и А1В1С1 ∠А=30°, АВ=1 м, ВС=2м,
В1С1 = 3м. Чему равны
∠А1 и сторона А1В1?
∠А1 и сторона А1В1?
С
В
А
А1
С1
В1
30°
1 м
3 м
2 м
Слайд 9Проверь себя
Что такое преобразование подобия?
Какие свойства преобразования подобия ты знаешь?
Что такое
коэффициент подобия?
Слайд 10Подобные фигур
Две фигуры называются подобными, если они переводятся друг в друга
преобразованием подобия
Проверь себя
Свойства подобных фигур
Задание 1
Задание 2
Иллюстрация определения
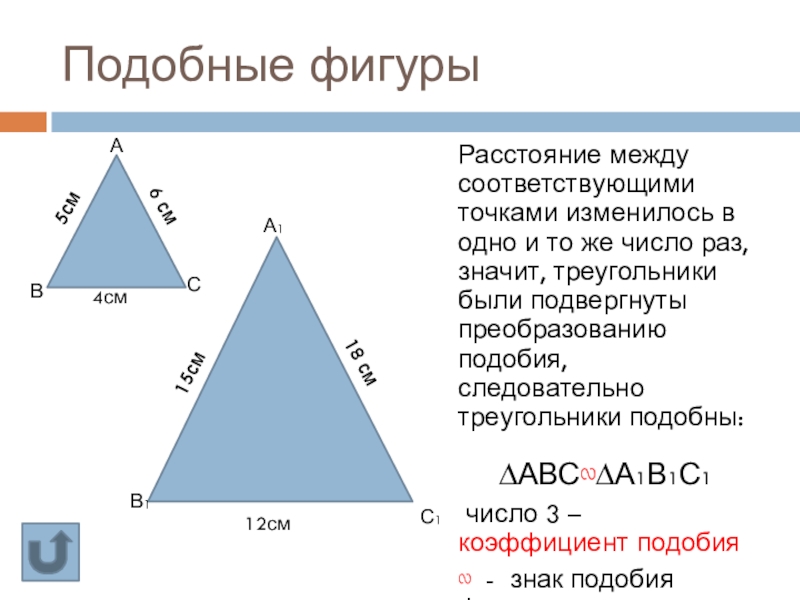
Слайд 11Подобные фигуры
Расстояние между соответствующими точками изменилось в одно и то же
число раз, значит, треугольники были подвергнуты преобразованию подобия, следовательно треугольники подобны:
∆АВС∾∆А1В1С1
число 3 – коэффициент подобия
∾ - знак подобия фигур
∆АВС∾∆А1В1С1
число 3 – коэффициент подобия
∾ - знак подобия фигур
А
А1
С
В
С1
В1
5см
15см
4см
12см
6 см
18 см
Слайд 12Свойства подобных фигур
Если фигура А подобна фигуре В, а фигура В
подобна фигуре С, то фигуры А и С подобны;
У подобных фигур соответствующие углы равны, а соответствующие отрезки пропорциональны.
У подобных фигур соответствующие углы равны, а соответствующие отрезки пропорциональны.
Пример 1
Пример 2
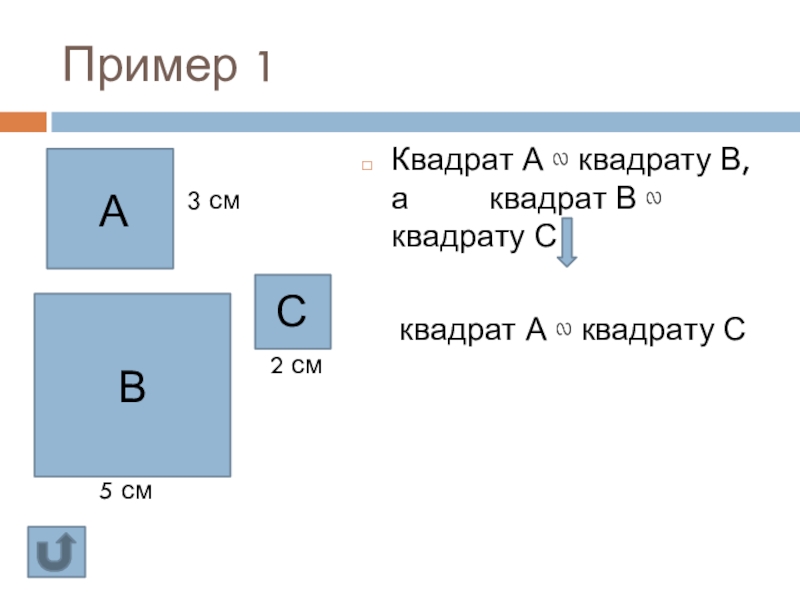
Слайд 13Пример 1
Квадрат А ∾ квадрату В, а
квадрат В ∾ квадрату С
квадрат А ∾ квадрату С
квадрат А ∾ квадрату С
А
С
В
3 см
2 см
5 см
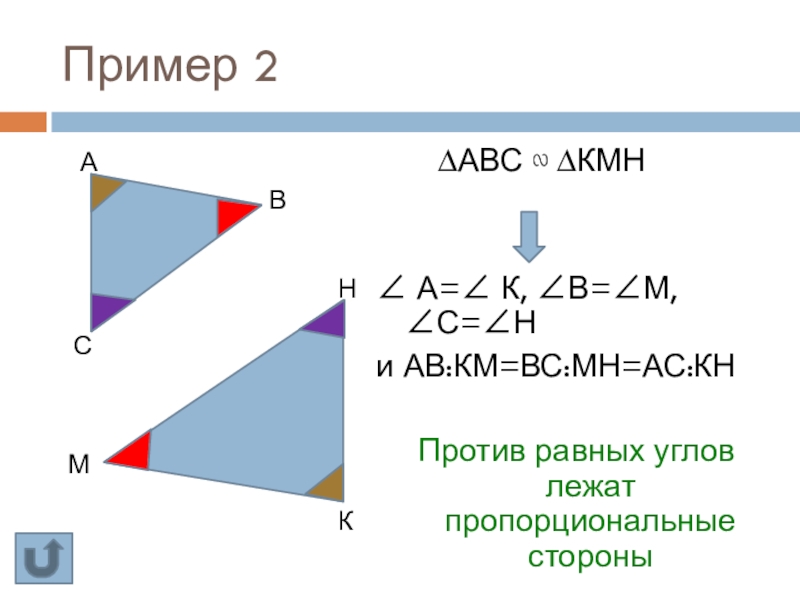
Слайд 14Пример 2
∆АВС ∾ ∆КМН
∠ А=∠ К, ∠В=∠М,
∠С=∠Н
и АВ:КМ=ВС:МН=АС:КН
Против равных углов лежат пропорциональные стороны
и АВ:КМ=ВС:МН=АС:КН
Против равных углов лежат пропорциональные стороны
А
С
В
К
Н
М
Слайд 15Задание 1
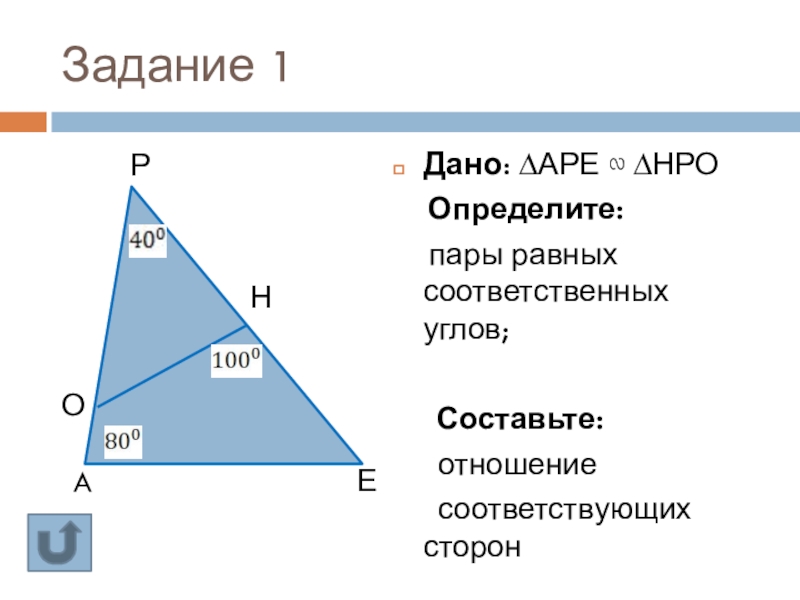
Дано: ∆АРЕ ∾ ∆НРО
Определите:
пары равных соответственных
углов;
Составьте:
отношение
соответствующих сторон
Составьте:
отношение
соответствующих сторон
A
Е
Р
О
Н
Слайд 17Проверь себя
Какие фигуры называются подобными?
Каким знаком обозначается подобие фигур?
Как записывается подобие
треугольников?
Слайд 18Признак подобия треугольников
по двум углам( I признак подобия)
Если два угла
одного треугольника равны двум углам другого треугольника, то такие треугольники подобны
Иллюстрация
I признака
Задание 1
Задание 3
Задание 2
Проверь себя
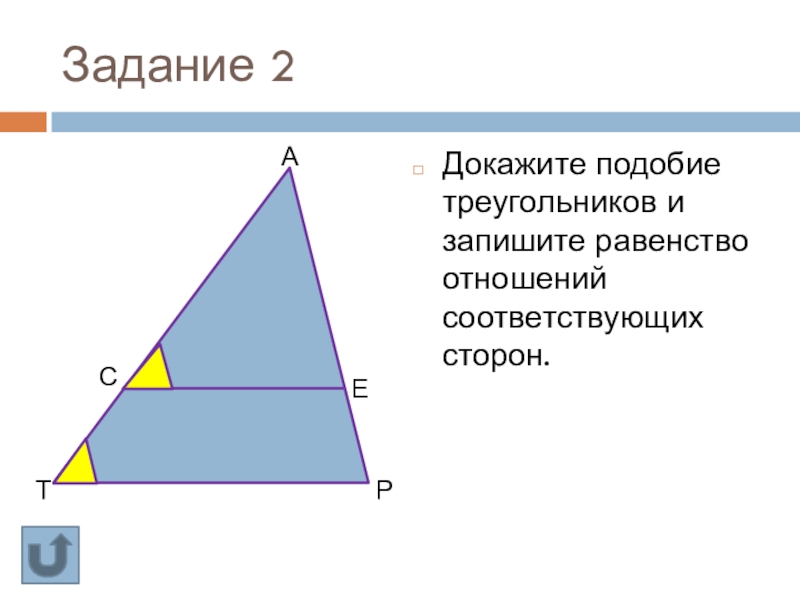
Слайд 21Задание 2
Докажите подобие треугольников и запишите равенство отношений соответствующих сторон.
А
Р
Т
С
Е
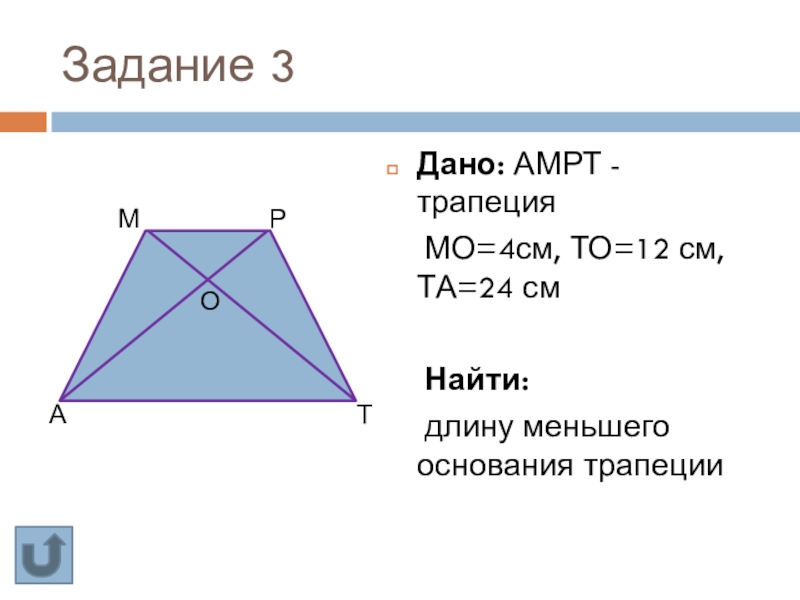
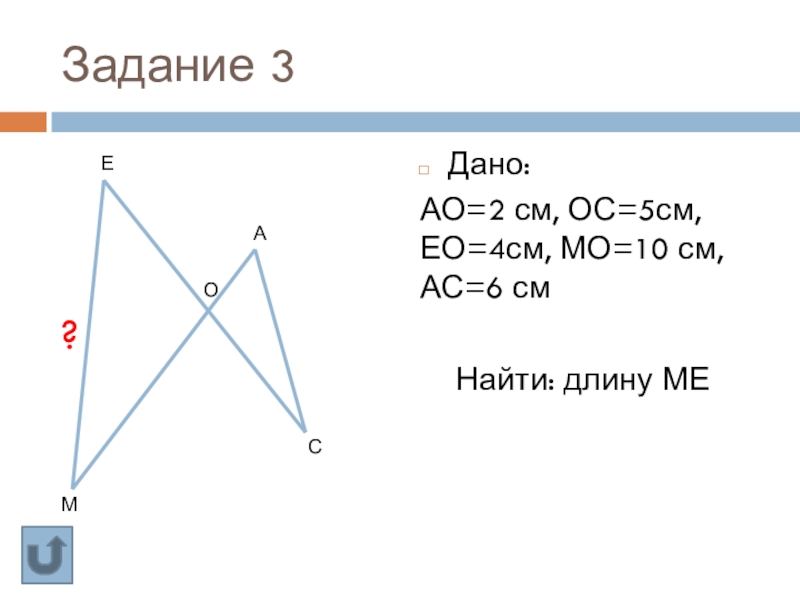
Слайд 22Задание 3
Дано: АМРТ - трапеция
МО=4см, ТО=12 см, ТА=24 см
Найти:
длину меньшего основания трапеции
А
Р
М
Т
О
Слайд 23Проверь себя
Какие условия должны выполняться для подобия треугольников по первому признаку?
Будут
ли подобны треугольники, если:
∆АВС: ∠А=65°, ∠В=80°, ∠С=35°
∆А1В1С1: ∠А1=35°, ∠В1=55°?
∆АВС: ∠А=65°, ∠В=80°, ∠С=35°
∆А1В1С1: ∠А1=35°, ∠В1=55°?
Слайд 24Признак подобия треугольников по двум сторонам и углу между ними (II
признак подобия)
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, образованные этими сторонами, равны, то треугольники подобны
Иллюстрация
II признака
Задание 1
Задание 2
Задание 3
Проверь себя
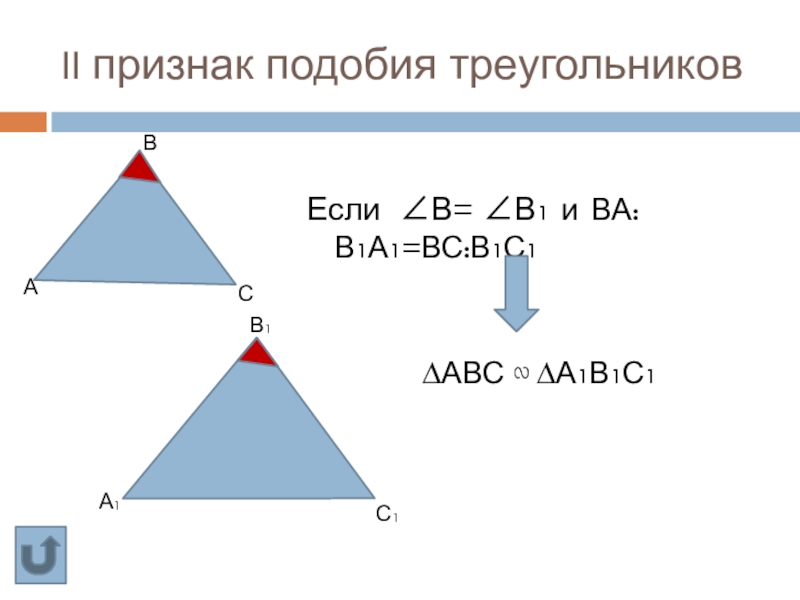
Слайд 25II признак подобия треугольников
Если ∠В= ∠В1 и ВА:В1А1=ВС:В1С1
А
В
С
А1
В1
С1
∆АВС ∾ ∆А1В1С1
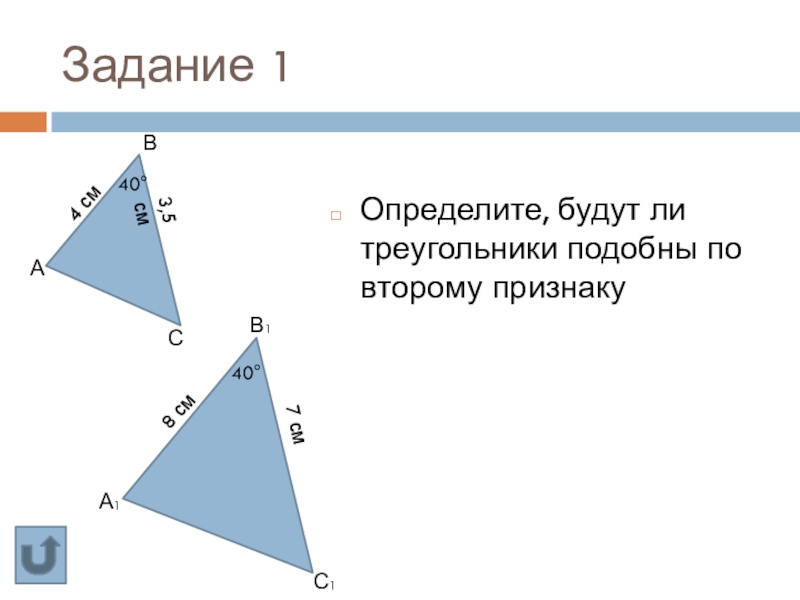
Слайд 26Задание 1
А
В
С
А1
В1
С1
Определите, будут ли треугольники подобны по второму признаку
40°
40°
4 см
3,5 см
8 см
7 см
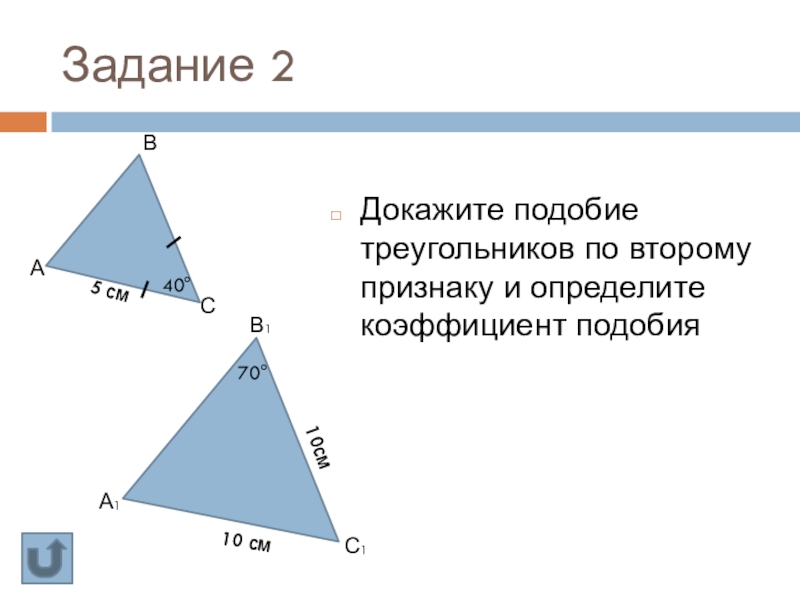
Слайд 27Задание 2
А
В
С
А1
В1
С1
Докажите подобие треугольников по второму признаку и определите коэффициент подобия
40°
70°
5 см
10 см
10см
Слайд 29Проверь себя
Перечисли условия для подобия треугольников по второму признаку.
Дополни условие
так, чтобы треугольники были подобны по второму признаку:
∆АВС: АВ=16 см, СА=20, ∠С=35°
∆А1В1С1: А1В1=4 см, ∠С1 =35°, С1А1= …
∆АВС: АВ=16 см, СА=20, ∠С=35°
∆А1В1С1: А1В1=4 см, ∠С1 =35°, С1А1= …
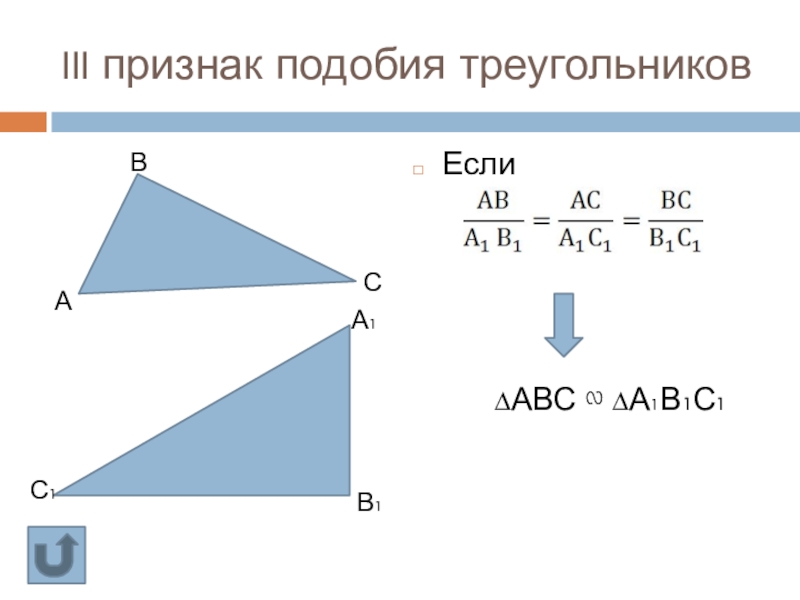
Слайд 30Признак подобия треугольников по трем сторонам (III признак подобия)
Если
стороны одного треугольника пропорциональны сторонам другого треугольника, то такие треугольники подобны
Иллюстрация III признака
Задание 1
Задание 2
Задание 3
Проверь себя
Слайд 33Задание 2
Подобны ли треугольники АВС и МРК, если:
АВ=1 м, АС=2 м,
ВС= 1,5 м и
МР=8м, МК=16 м, РК=12 м;
АВ=1 м, АС=2 м, ВС= 1,25 м и
МР=10м, МК=20 м, РК=13 м;
МР=8м, МК=16 м, РК=12 м;
АВ=1 м, АС=2 м, ВС= 1,25 м и
МР=10м, МК=20 м, РК=13 м;
Слайд 34Задание 3
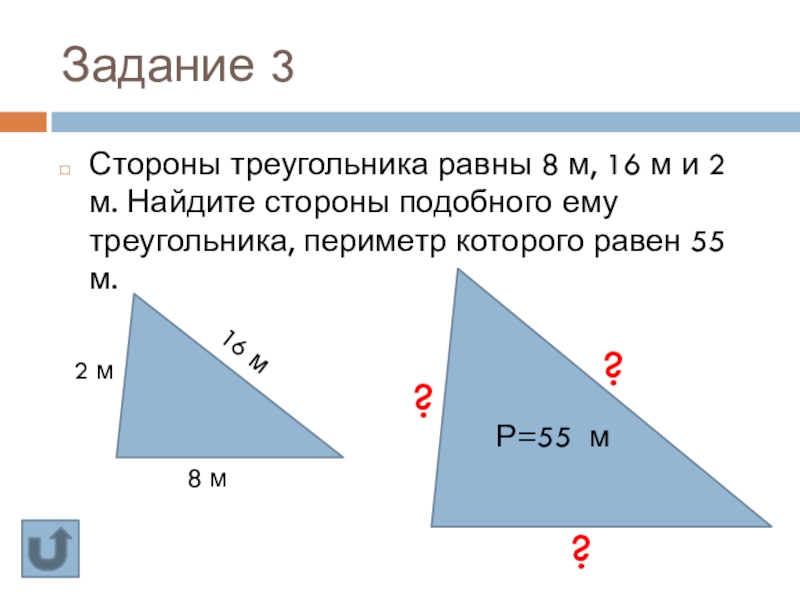
Стороны треугольника равны 8 м, 16 м и 2 м.
Найдите стороны подобного ему треугольника, периметр которого равен 55 м.
8 м
2 м
16 м
Р=55 м
?
?
?
Слайд 35Проверь себя
Сформулируй условие, при котором треугольники будут подобны по III признаку
подобия.
Измени условие так, чтобы треугольники были подобны по III признаку:
∆АВС : АВ=12 см, ВС=15 см, АС=18 см
∆А1В1С1 : А1В1 =24 см, С1А1 =45 см, В1С1 = 30 см
Измени условие так, чтобы треугольники были подобны по III признаку:
∆АВС : АВ=12 см, ВС=15 см, АС=18 см
∆А1В1С1 : А1В1 =24 см, С1А1 =45 см, В1С1 = 30 см
Слайд 36Подобие прямоугольных треугольников
Для подобия прямоугольных треугольников достаточно, чтобы у
них было по одному острому углу
Иллюстрация признака подобия
Задание 1
Задание 2
Задание 3
Проверь себя
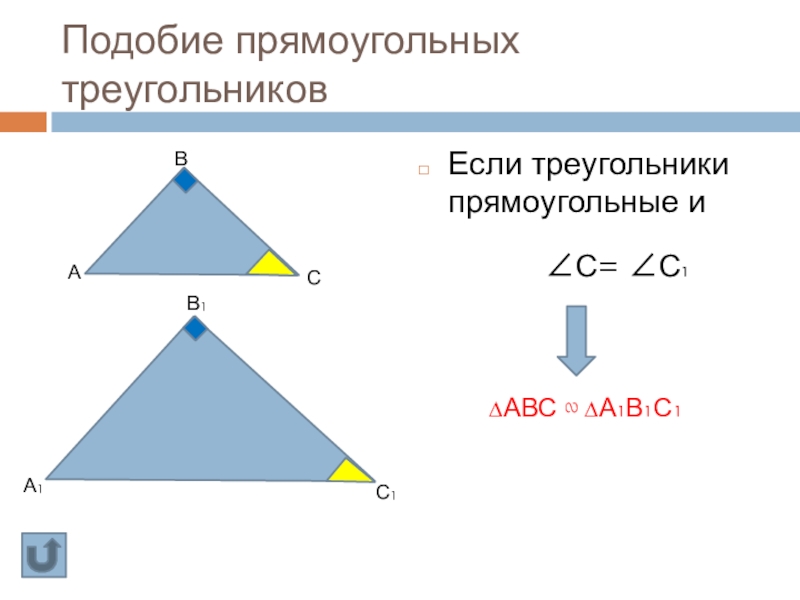
Слайд 37Подобие прямоугольных треугольников
Если треугольники прямоугольные и
∠С= ∠С1
А
А1
В
С
В1
С1
∆АВС ∾ ∆А1В1С1
Слайд 39Задание 2
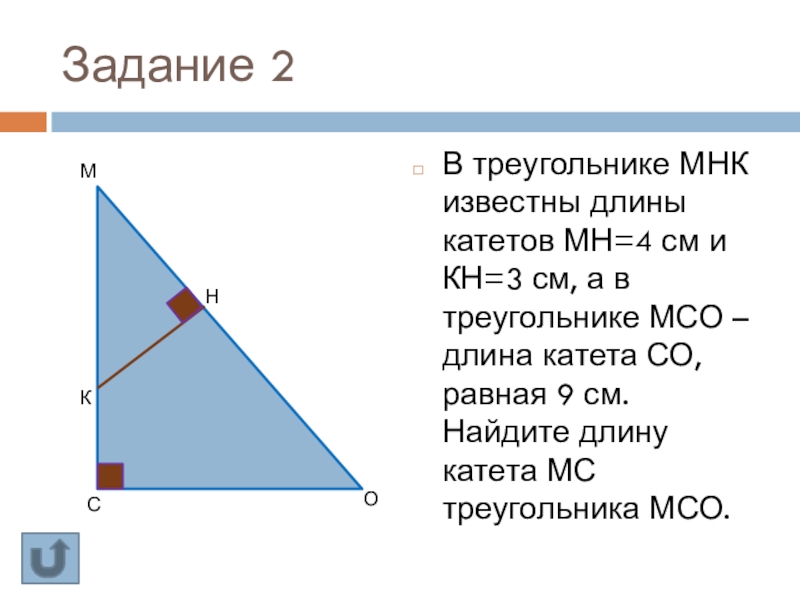
В треугольнике МНК известны длины катетов МН=4 см и КН=3
см, а в треугольнике МСО – длина катета СО, равная 9 см. Найдите длину катета МС треугольника МСО.
М
С
О
К
Н
Слайд 41Проверь себя
Назовите условие, при котором прямоугольные треугольники подобны.
Будут ли подобны
прямоугольные треугольники, если у одного острый угол равен 40°, а у другого – 50 °?
