- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по теме Правильные многогранники (тетраэдр)-10 кл
Содержание
- 1. Презентация по теме Правильные многогранники (тетраэдр)-10 кл
- 2. Понятие тетраэдраПирамида, в основании которой лежит треугольник,
- 3. Построение тетраэдраИзображают обычно тетраэдр как четырехугольник с диагоналями, одну из которых (соответствующую невидимому ребру) изображают пунктирно.АВСD
- 4. ТетраэдрDАВС – тетраэдрА, В, С, D –
- 5. Определения медианы, бимедианы и высоты тетраэдраОтрезок, соединяющий
- 6. Элементы симметрии тетраэдраТетраэдр имеет три оси симметрии,
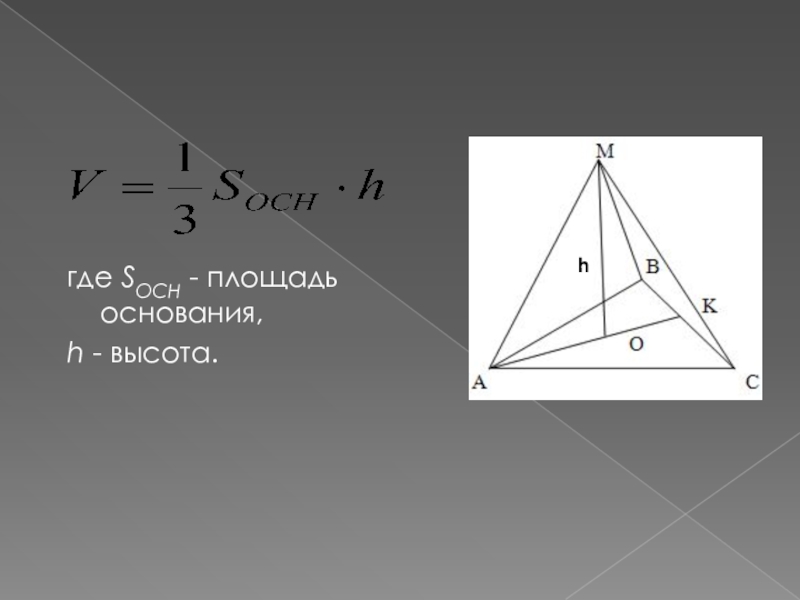
- 7. Объем пирамиды где SОСН - площадь основания, h - высота.h
- 8. Площадь поверхности пирамиды
- 9. Типы тетраэдровРавногранный тетраэдр – это тетраэдр, у
- 10. Правильный тетраэдрТетраэдр, все четыре грани которого —
- 11. Все четыре грани правильного тетраэдра – правильные
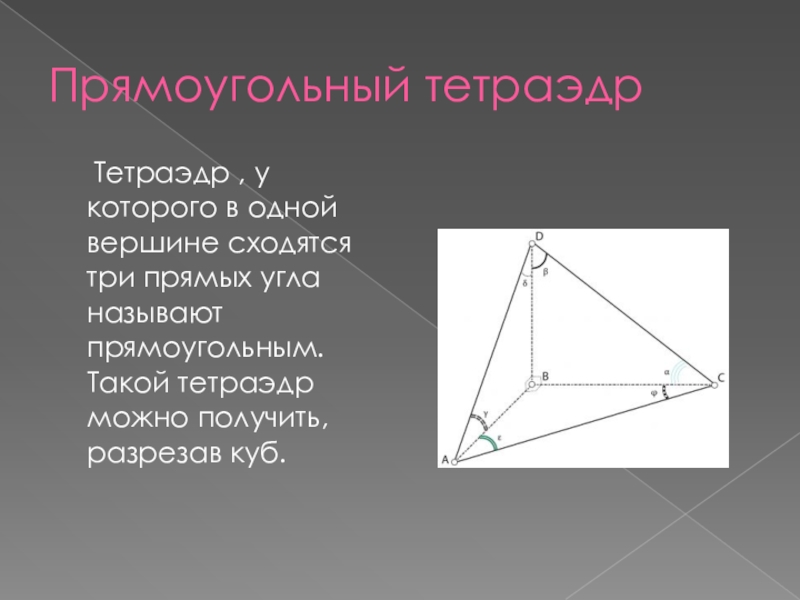
- 12. Прямоугольный тетраэдр Тетраэдр , у
- 13. Тетраэдры в живой природе
- 14. Тетраэдры в строительстве Тетраэдр
- 15. Тетраэдр в оптике Прямоугольный
- 16. Тетраэдры в микромиреМолекула метана СН4Молекула аммиака NH3Алмаз
- 17. Тетраэдры в производстве Форму тетраэдра
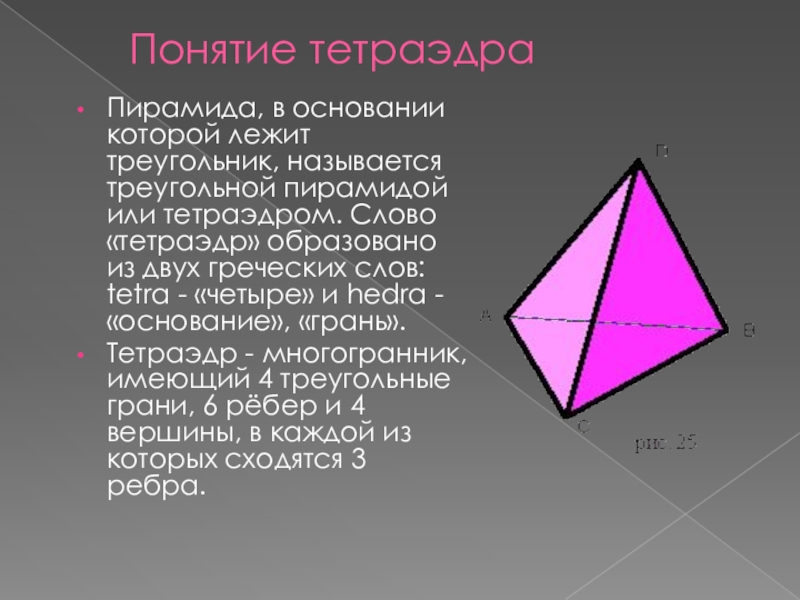
Понятие тетраэдраПирамида, в основании которой лежит треугольник, называется треугольной пирамидой или тетраэдром. Слово «тетраэдр» образовано из двух греческих слов: tetra - «четыре» и hedra - «основание», «грань». Тетраэдр - многогранник, имеющий 4 треугольные грани, 6 рёбер
Слайд 1Тетраэдр
Правильные многогранники
10 класс
Е.И.Мироненко
Учитель математики
Первая квалификационная категория
Слайд 2Понятие тетраэдра
Пирамида, в основании которой лежит треугольник, называется треугольной пирамидой или
тетраэдром. Слово «тетраэдр» образовано из двух греческих слов: tetra - «четыре» и hedra - «основание», «грань».
Тетраэдр - многогранник, имеющий 4 треугольные грани, 6 рёбер и 4 вершины, в каждой из которых сходятся 3 ребра.
Тетраэдр - многогранник, имеющий 4 треугольные грани, 6 рёбер и 4 вершины, в каждой из которых сходятся 3 ребра.
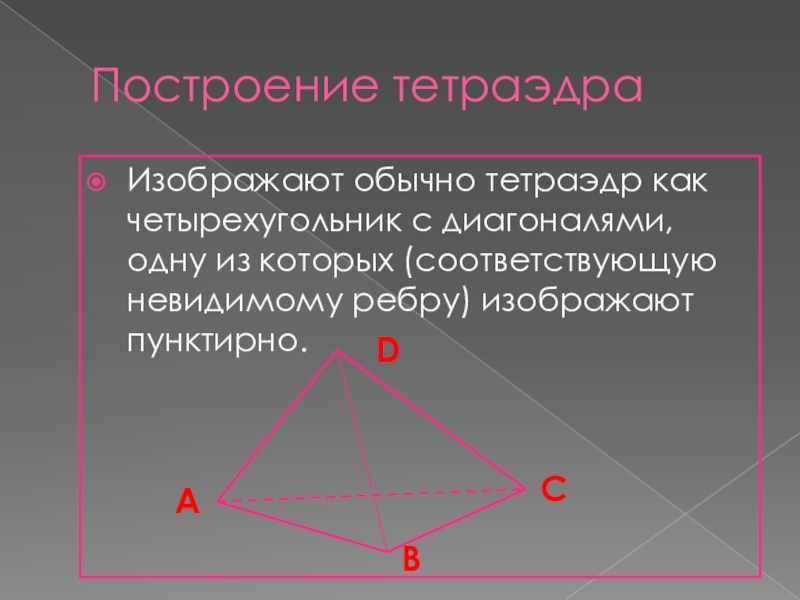
Слайд 3Построение тетраэдра
Изображают обычно тетраэдр как четырехугольник с диагоналями, одну из которых
(соответствующую невидимому ребру) изображают пунктирно.
А
В
С
D
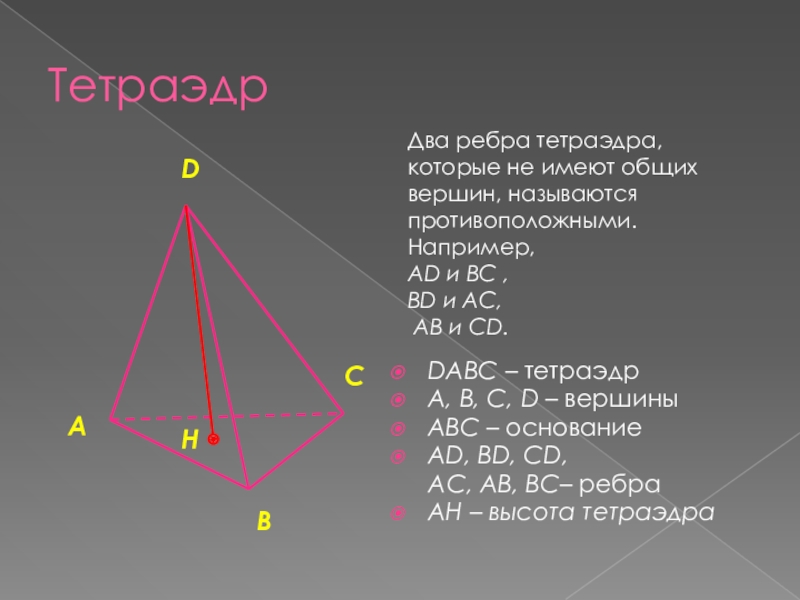
Слайд 4Тетраэдр
DАВС – тетраэдр
А, В, С, D – вершины
АВС – основание
АD, ВD,
СD,
АС, АВ, ВС– ребра
АH – высота тетраэдра
АС, АВ, ВС– ребра
АH – высота тетраэдра
C
A
B
D
H
Два ребра тетраэдра, которые не имеют общих вершин, называются противоположными. Например,
АD и ВС ,
ВD и АС,
АВ и СD.
Слайд 5Определения медианы, бимедианы и высоты тетраэдра
Отрезок, соединяющий вершину тетраэдра с точкой
пересечения медиан противоположной грани, называется его медианой, опущенной из данной вершины.
Отрезок, соединяющий середины скрещивающихся рёбер тетраэдра, называется его бимедианой, соединяющей данные рёбра.
Отрезок, соединяющий вершину с точкой противоположной грани и перпендикулярный этой грани, называется его высотой, опущенной из данной вершины.
Отрезок, соединяющий середины скрещивающихся рёбер тетраэдра, называется его бимедианой, соединяющей данные рёбра.
Отрезок, соединяющий вершину с точкой противоположной грани и перпендикулярный этой грани, называется его высотой, опущенной из данной вершины.
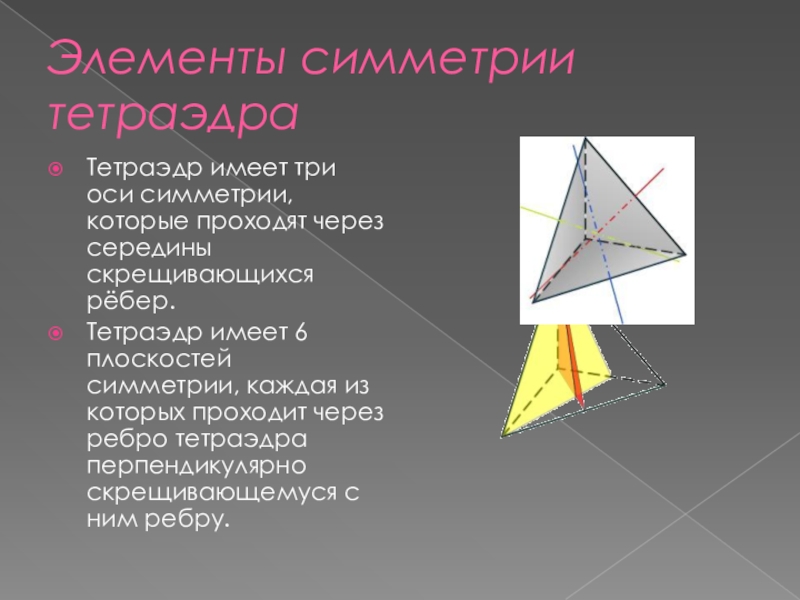
Слайд 6Элементы симметрии тетраэдра
Тетраэдр имеет три оси симметрии, которые проходят через середины
скрещивающихся рёбер.
Тетраэдр имеет 6 плоскостей симметрии, каждая из которых проходит через ребро тетраэдра перпендикулярно скрещивающемуся с ним ребру.
Тетраэдр имеет 6 плоскостей симметрии, каждая из которых проходит через ребро тетраэдра перпендикулярно скрещивающемуся с ним ребру.
Слайд 9Типы тетраэдров
Равногранный тетраэдр – это тетраэдр, у которого все грани –
равные между собой треугольники.
Ортоцентрический тетраэдр – это тетраэдр, у которого все высоты, опущенные из вершин на противоположные грани, пересекаются в одной точке.
Прямоугольный тетраэдр – это тетраэдр, у которого все ребра, прилежащие к одной из вершин, перпендикулярны между собой.
Правильный тетраэдр – это тетраэдр, у которого все грани — равносторонние треугольники.
Соразмерный тетраэдр, бивысоты которого равны.
Инцентрический тетраэдр –это тетраэдр, у которого отрезки, соединяющие вершины тетраэдра с центрами окружностей, вписанных в противоположные грани, пересекаются в одной точке.
Ортоцентрический тетраэдр – это тетраэдр, у которого все высоты, опущенные из вершин на противоположные грани, пересекаются в одной точке.
Прямоугольный тетраэдр – это тетраэдр, у которого все ребра, прилежащие к одной из вершин, перпендикулярны между собой.
Правильный тетраэдр – это тетраэдр, у которого все грани — равносторонние треугольники.
Соразмерный тетраэдр, бивысоты которого равны.
Инцентрический тетраэдр –это тетраэдр, у которого отрезки, соединяющие вершины тетраэдра с центрами окружностей, вписанных в противоположные грани, пересекаются в одной точке.
Слайд 10Правильный тетраэдр
Тетраэдр, все четыре грани которого — равные правильные треугольники, называется
правильным тетраэдром .
Правильный тетраэдр — это частный случай правильной треугольной пирамиды.
Правильный тетраэдр — это частный случай правильной треугольной пирамиды.
Слайд 11Все четыре грани правильного тетраэдра – правильные треугольники. Если длину ребра правильного
тетраэдра обозначить a, то можно вычислить:
Правильный тетраэдр
Слайд 12Прямоугольный тетраэдр
Тетраэдр , у которого в одной вершине
сходятся три прямых угла называют прямоугольным. Такой тетраэдр можно получить, разрезав куб.
Слайд 13Тетраэдры в живой природе
Некоторые плоды, находясь вчетвером
на одной кисти, располагаются в вершинах тетраэдра, близкого к правильному. Такая конструкция обусловлена тем, что центры четырёх одинаковых шаров, касающихся друг друга, находятся в вершинах правильного тетраэдра. Поэтому похожие на шар плоды образуют подобное взаимное расположение. Например, таким образом могут располагаться грецкие орехи.
Слайд 14Тетраэдры в строительстве
Тетраэдр образует жёсткую, статически определимую
конструкцию. Тетраэдр, выполненный из стержней, часто используется в качестве основы для пространственных несущих конструкций пролётов зданий, перекрытий, балок, ферм, мостов и т. д. Стержни испытывают только продольные нагрузки.
Слайд 15Тетраэдр в оптике
Прямоугольный тетраэдр используется в оптике.
Если грани, имеющие прямой угол, покрыть светоотражающим составом или весь тетраэдр выполнить из материала с сильным светопреломлением, чтобы возникал эффект полного внутреннего отражения, то свет, направленный в грань, противоположную вершине с прямыми углами, будет отражаться в том же направлении, откуда он пришёл. Это свойство используется для создания уголковых отражателей, катафотов.
Слайд 16Тетраэдры в микромире
Молекула метана СН4
Молекула аммиака NH3
Алмаз C — тетраэдр с
ребром равным 2,5220 ангстрем
Флюорит CaF2, тетраэдр с ребром равным 3, 8626 ангстрем
Сфалерит, ZnS, тетраэдр с ребром равным 3,823 ангстрем
Комплексные ионы [BF4] -, [ZnCl4]2-, [Hg(CN)4]2-, [Zn(NH3)4]2+
Силикаты, в основе структур которых лежит кремнекислородный тетраэдр [SiO4]4-
Флюорит CaF2, тетраэдр с ребром равным 3, 8626 ангстрем
Сфалерит, ZnS, тетраэдр с ребром равным 3,823 ангстрем
Комплексные ионы [BF4] -, [ZnCl4]2-, [Hg(CN)4]2-, [Zn(NH3)4]2+
Силикаты, в основе структур которых лежит кремнекислородный тетраэдр [SiO4]4-
Слайд 17Тетраэдры в производстве
Форму тетраэдра нельзя назвать удобной, но
и у нее есть применение, например, при изготовлении пакетов для молока. Оказалось, что на конвейере удобно склеивать подобные тетраэдры, отрезая заготовки для них от картонного “шланга”.