Ярославль, 2017
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по теме Правильные многогранники (11 класс)
Содержание
- 1. Презентация по теме Правильные многогранники (11 класс)
- 2. История
- 3. Древнейшие временаИстория правильных многогранников уходит в глубокую
- 4. Античная философия Начиная с 7 века до
- 5. Слайд 5
- 6. Античная философия Правильные многогранники характерны для философии
- 7. Слайд 7
- 8. ГеометрияЕвклид дал полное математическое описание правильных многогранников
- 9. Определение, свойства…
- 10. ОпределениеПравильный многогранник – выпуклый многогранник, грани которого
- 11. Пять типов правильных многогранниковРассмотрим правильный многогранник{p, q}По теореме Декарта-Эйлера:В-Р+Г=2Для Г-гранника с Р ребрами и В вершинами.
- 12. Пять типов правильных многогранников
- 13. Пять типов правильных многогранников
- 14. Пять типов правильных многогранников
- 15. Пять типов правильных многогранников
- 16. Правильный тетраэдр{3, 3}Г=4В=4Р=6
- 17. Правильный гексаэдр (куб){4, 3}Г=6В=8Р=12
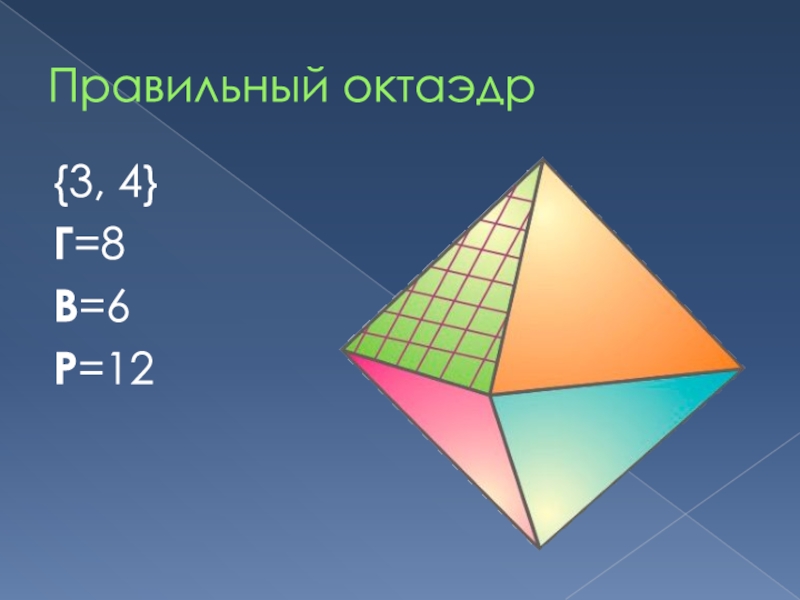
- 18. Правильный октаэдр{3, 4}Г=8В=6Р=12
- 19. {5, 3}Г=12В=20Р=30Правильный додекаэдр
- 20. {3, 5}Г=20В=12Р=30Правильный икосаэдр
- 21. СвойстваС каждым правильным многогранником связаны определённые углы,
- 22. СвойстваС каждым правильным многогранником связаны три концентрические
- 23. СвойстваРадиусы сфер: --------
- 24. СвойстваПлощадь поверхности S правильного многогранника {p, q}
- 25. СвойстваОбъём правильного многогранника вычисляется, как умноженный на
- 26. Слайд 26
- 27. Спасибо за внимание!
История
Слайд 1Правильные многогранники
Выполнил: Холявко Игорь,
ученик 11-1 класса
Руководитель: Иванова О.К.,
учитель
математики
Слайд 3Древнейшие времена
История правильных многогранников уходит в глубокую древность. Их орнаментные модели
можно найти на резных каменных шарах, созданных в период
позднего неолита.
В костях, которыми люди
играли на заре цивилизации,
уже угадываются формы
правильных многогранников.
позднего неолита.
В костях, которыми люди
играли на заре цивилизации,
уже угадываются формы
правильных многогранников.
Слайд 4Античная философия
Начиная с 7 века до нашей эры в Древней
Греции создаются философские школы. Одной из первых и самых известных школ была Пифагорейская, названная в честь своего основателя Пифагора.
Существование пяти
правильных многогранников пифагорейцы относили к строению материи и Вселенной.
Существование пяти
правильных многогранников пифагорейцы относили к строению материи и Вселенной.
Слайд 6Античная философия
Правильные многогранники характерны для философии Платона, в честь которого
они и получили название «Платоновы тела». Платон писал о них в своём трактате в 360г до н. э., где сопоставил каждую из четырёх стихий определённому правильному многограннику. Земля сопоставлялась кубу, воздух — октаэдру, вода — икосаэдру, а огонь — тетраэдру.
По поводу пятого элемента, додекаэдра, Платон сделал смутное замечание: «его бог определил для Вселенной и прибегнул к нему в качестве образца».
По поводу пятого элемента, додекаэдра, Платон сделал смутное замечание: «его бог определил для Вселенной и прибегнул к нему в качестве образца».
Слайд 8Геометрия
Евклид дал полное математическое описание правильных многогранников в последней, XIII книге
«Начал». . Для каждого многогранника Евклид нашёл отношение диаметра описанной сферы к длине ребра.
Слайд 10Определение
Правильный многогранник – выпуклый многогранник, грани которого являются равными правильными многоугольниками,
и в каждой вершине сходится одинаковое число ребер.
Правильный многогранник может быть описан символом Шлефли {p, q}
p – рёбер содержит одна грань
q – рёбер сходится в каждой вершине
Правильный многогранник может быть описан символом Шлефли {p, q}
p – рёбер содержит одна грань
q – рёбер сходится в каждой вершине
Слайд 11Пять типов правильных многогранников
Рассмотрим правильный многогранник
{p, q}
По теореме Декарта-Эйлера:
В-Р+Г=2
Для Г-гранника с
Р ребрами и В вершинами.
Слайд 21Свойства
С каждым правильным многогранником связаны определённые углы, характеризующие его свойства. Двугранный
угол между смежными гранями правильного многогранника {p, q} задаётся формулой:
Слайд 22Свойства
С каждым правильным многогранником связаны три концентрические сферы:
Описанная сфера, проходящая через
вершины многогранника;
Срединная сфера, касающаяся каждого его ребра в середине;
Вписанная сфера, касающаяся каждой его грани в её центре.
Срединная сфера, касающаяся каждого его ребра в середине;
Вписанная сфера, касающаяся каждой его грани в её центре.
Слайд 24Свойства
Площадь поверхности S правильного многогранника {p, q} вычисляется, как площадь правильного
p-угольника, умноженная на число граней Г:
Слайд 25Свойства
Объём правильного многогранника вычисляется, как умноженный на число граней объём правильной
пирамиды, основанием которой служит правильный p-угольник, а высотой — радиус вписанной сферы r: