и
Клипачёва Светлана
Ученица 9 класса «Г»
Учитель: И. А. Иванченко
Ростов 2019
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по теме Параллелограмм
Содержание
- 1. Презентация по теме Параллелограмм
- 2. Параллелограмм
- 3. Цель: 1) Обобщить тему «Параллелограм»Задачи:1)Узнать историю возникновения понятия
- 4. ОпределениеПараллелогра́мм — это четырёхугольник, у которого противоположные
- 5. История созданияТермин "ПАРАЛЛЕЛОГРАММ" греческого происхождения и был
- 6. Свойства параллелограмма 1)В параллелограмме противоположные стороны равны,
- 7. Свойства параллелограмма2)В параллелограмме диагонали точкой пересечения делятся
- 8. Признаки параллелограмма1)Если в четырехугольнике противоположные стороны равны,
- 9. Признаки параллелограмма2) Если в четырехугольнике диагонали точкой
- 10. Признаки параллелограмма 3)Если в четырехугольнике одна пара
- 11. Площади параллелограмма 1. Площадь параллелограмма равна произведению
- 12. Площади параллелограмма2. Если известны длины двух смежных
- 13. Площади параллелограмма3. Если заданы диагонали параллелограмма и
- 14. Периметр параллелограмма Периметр параллелограмма равен удвоенной сумме
- 15. Параллелограмм в жизни
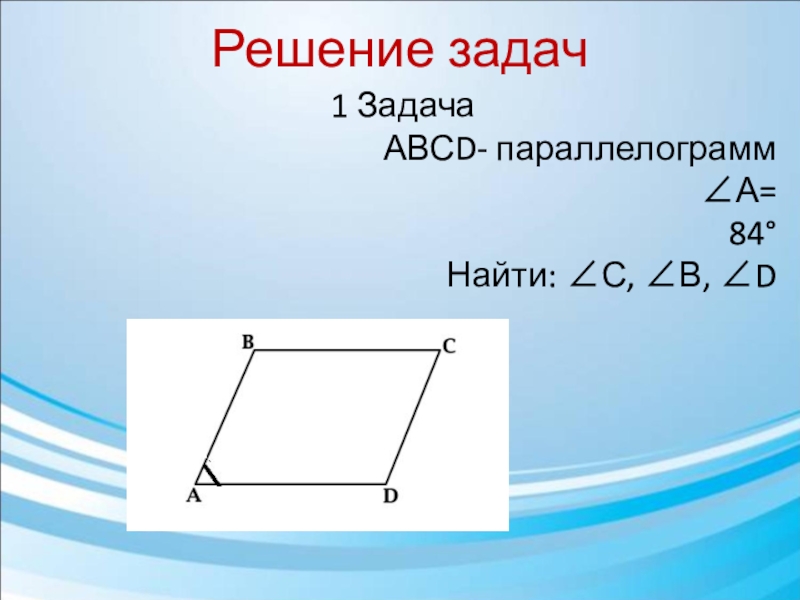
- 16. Решение задач1 Задача АВСD- параллелограмм
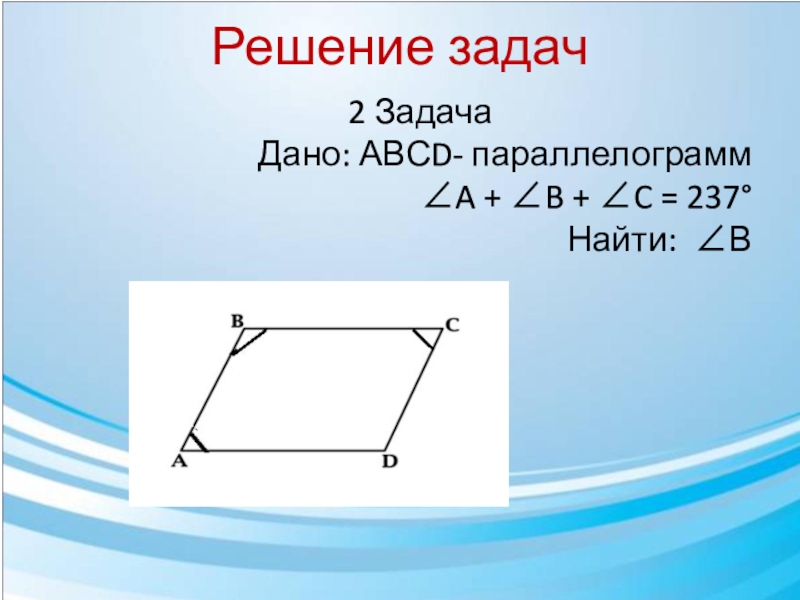
- 17. Решение задач 2 Задача
- 18. Решение задач3 ЗадачаДано: АВСD- параллелограмм∠САD=16°,∠ACD=37° Найти: ∠А, ∠В, ∠ C,∠D.
- 19. Решение задач4 ЗадачаВысота  ромба  делит
- 20. Решение задач 5 ЗадачаПлощадь параллелограмма ABCD равна
- 21. Решение задач 6 Задача Периметр параллелограмма АВСD
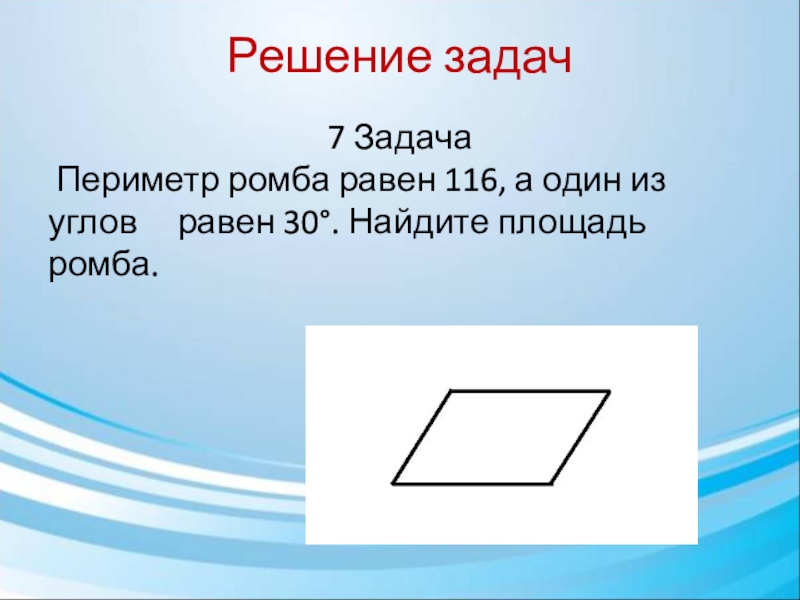
- 22. Решение задач 7 Задача Периметр ромба равен
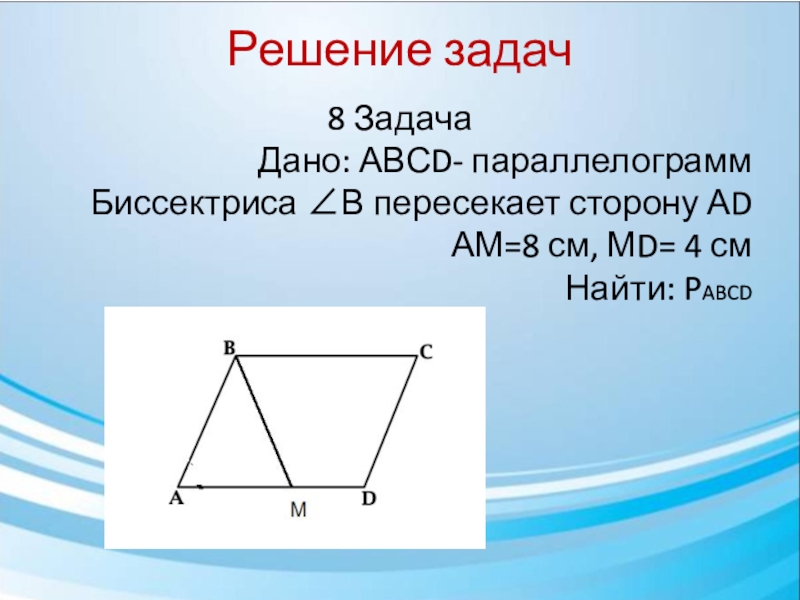
- 23. Решение задач 8 Задача Дано: АВСD- параллелограммБиссектриса ∠В пересекает сторону АDАМ=8 см, МD= 4 смНайти: PABCD
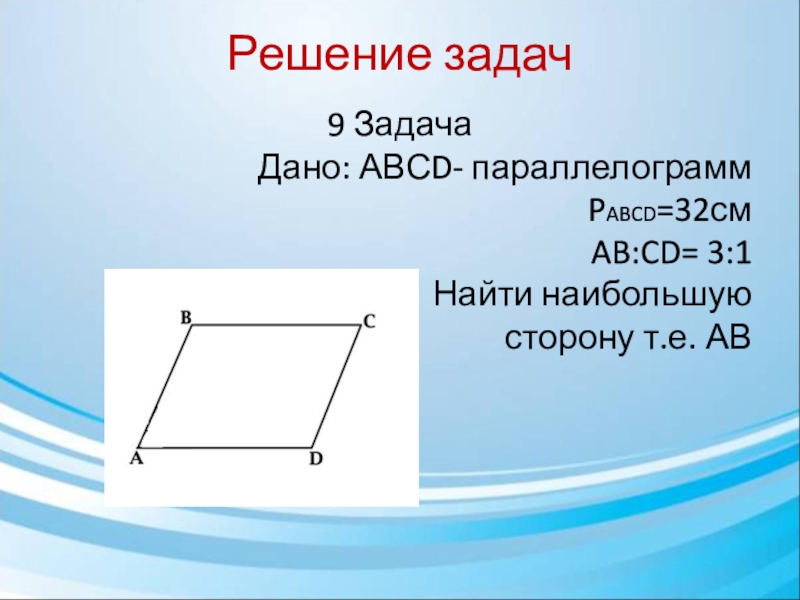
- 24. Решение задач 9 ЗадачаДано: АВСD- параллелограммPABCD=32смAB:CD= 3:1 Найти наибольшую сторону т.е. АВ
- 25. Решение задач 10 Задача Периметр параллелограмма ABCD
- 26. Решение1 Задача 1)ABCD - параллелограмм ⇒ ∠А
- 27. Решение2 Задача 1)Т.к. ∠A + ∠B +
- 28. Решение3 Задача 1)ABCD - параллелограмм ⇒ ∠А
- 29. Решение4 Задача Из прямоугольного треугольника  найдём
- 30. Решение5 Задача Диагональ параллелограмма делит его на
- 31. Решение6 Задача Проведём высоту BH.Треугольник AHB –
- 32. Решение 7 Задача Решение: Обозначим CD за
- 33. Решение 8 Задача AD= AM+MD= 8+4 =12AD
- 34. Решение 9 Задача Проведём высоту в ромбе
- 35. Решение 10 ЗадачаРABCD= 2*(AB+AD), поэтому AB+ AD=
- 36. Источникиhttp://worksbase.ru/matematika/formuly/1031-parallelogramm.htmlhttp://www.webmath.ru/poleznoe/formules13.phphttp://ru.solverbook.com/spravochnik/formuly-po-geometrii/formuly-perimetra/perimetr-parallelogramma/
Параллелограмм
Слайд 1МОУ гимназия имени А. Л. Кекина
Презентация на тему:
«Параллелограмм»
Выполнила: Клипачёва Полина
Слайд 3Цель:
1) Обобщить тему «Параллелограм»
Задачи:
1)Узнать историю возникновения понятия «параллелограмм».
2) Познакомиться с
понятием «Параллелограмм».
3)Изучить свойства и виды параллелограмма.
4)Показать применение свойств и признаков параллелограмма при решении задач.
3)Изучить свойства и виды параллелограмма.
4)Показать применение свойств и признаков параллелограмма при решении задач.
Слайд 4Определение
Параллелогра́мм — это четырёхугольник, у которого противоположные стороны попарно параллельны, то
есть лежат на параллельных прямых.
Параллелограммом являются:
Ромб
-Прямоугольник
-Квадрат
Параллелограммом являются:
Ромб
-Прямоугольник
-Квадрат
Слайд 5История создания
Термин "ПАРАЛЛЕЛОГРАММ" греческого происхождения и был введен Евклидом. Евклидом доказывается
теорема о том, что в параллелограмме противоположные стороны равны и противоположные углы равны, а диагональ разделяет его пополам, но Евклид не упоминает о том, что точка пересечения диагоналей делит их пополам.
Слайд 6Свойства параллелограмма
1)В параллелограмме противоположные стороны равны, противоположные углы равны.
Дано:
АВСD –
параллелограмм
Доказать:
AB = CD , BC = AD
∠A = ∠C , ∠B = ∠D
1. Построим диагональ BD
2. Треугольники ΔABD = ΔCBD равны :
1) BD - общая ; 2) ∠ADB = ∠CBD ; 3) ∠BDC = ∠DBA
3. Так как треугольники равны, то равны все соответственные элементы.
Доказать:
AB = CD , BC = AD
∠A = ∠C , ∠B = ∠D
1. Построим диагональ BD
2. Треугольники ΔABD = ΔCBD равны :
1) BD - общая ; 2) ∠ADB = ∠CBD ; 3) ∠BDC = ∠DBA
3. Так как треугольники равны, то равны все соответственные элементы.
Слайд 7Свойства параллелограмма
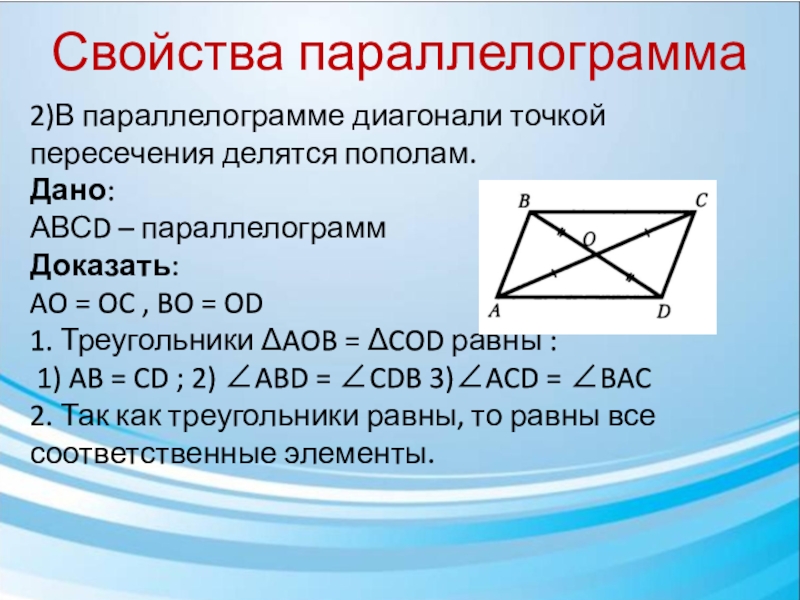
2)В параллелограмме диагонали точкой пересечения делятся пополам.
Дано:
АВСD – параллелограмм
Доказать:
AO
= OC , BO = OD
1. Треугольники ΔAOB = ΔCOD равны :
1) AB = CD ; 2) ∠ABD = ∠CDB 3)∠ACD = ∠BAC
2. Так как треугольники равны, то равны все соответственные элементы.
1. Треугольники ΔAOB = ΔCOD равны :
1) AB = CD ; 2) ∠ABD = ∠CDB 3)∠ACD = ∠BAC
2. Так как треугольники равны, то равны все соответственные элементы.
Слайд 8Признаки параллелограмма
1)Если в четырехугольнике противоположные стороны равны, то этот четырехугольник -параллелограмм
.
Дано:
ABCD – четырехугольник
AB = CD , BC = AD
Доказать :
АВСD – параллелограмм
Доказательство:
Рассмотрим ΔABС и ΔADC :
1)AC – общая ; 2) AB = CD ; 3) BC = AD (по условию) ⇒ ΔABС =ΔADC
(по 3 пр. равенства Δ)
∠1 = ∠2 ( н/л при прямых BC и AD и секущей AC ) ⇒ BC ∥ AD
∠3= ∠4 ( н/л при прямых CD и AB и секущей AC ) ⇒ CD ∥ AB
То BC ∥ AD ; CD ∥ AB ⇒ АВСD – параллелограмм
Дано:
ABCD – четырехугольник
AB = CD , BC = AD
Доказать :
АВСD – параллелограмм
Доказательство:
Рассмотрим ΔABС и ΔADC :
1)AC – общая ; 2) AB = CD ; 3) BC = AD (по условию) ⇒ ΔABС =ΔADC
(по 3 пр. равенства Δ)
∠1 = ∠2 ( н/л при прямых BC и AD и секущей AC ) ⇒ BC ∥ AD
∠3= ∠4 ( н/л при прямых CD и AB и секущей AC ) ⇒ CD ∥ AB
То BC ∥ AD ; CD ∥ AB ⇒ АВСD – параллелограмм
Слайд 9Признаки параллелограмма
2) Если в четырехугольнике диагонали точкой пересечения делятся пополам, то
этот четырехугольник- параллелограмм
Дано:
ABCD – четырехугольник
AC ∩ BD = O
BO = OD , AO = OC
Доказать :
АВСD – параллелограмм
Доказательство:
Рассмотрим ΔBOC и ΔAOD :
1)BO = OD (по условию) ; 2) AO = OC (по условию); 3) ∠BOC и ∠AOD (вертик.)
⇒ ΔBOC = ΔAOD (по 1-му признаку равенства Δ)
∠1 = ∠2 ( н/л при прямых BC и AD и секущей AC ) ⇒ BC ∥ AD
Рассмотрим ΔAOB и ΔCOD
1) ΔCOD = ΔBOA (вертик.) ; 2) ) AO = OC (по условию); 3) BO = OD (по условию)
⇒ ΔAOB = ΔCOD (по 1-му признаку равенства Δ)
∠3= ∠4 ( н/л при прямых CD и AB и секущей AC ) ⇒ CD ∥ AB
То BC ∥ AD ; CD ∥ AB ⇒АВСD – параллелограмм
Дано:
ABCD – четырехугольник
AC ∩ BD = O
BO = OD , AO = OC
Доказать :
АВСD – параллелограмм
Доказательство:
Рассмотрим ΔBOC и ΔAOD :
1)BO = OD (по условию) ; 2) AO = OC (по условию); 3) ∠BOC и ∠AOD (вертик.)
⇒ ΔBOC = ΔAOD (по 1-му признаку равенства Δ)
∠1 = ∠2 ( н/л при прямых BC и AD и секущей AC ) ⇒ BC ∥ AD
Рассмотрим ΔAOB и ΔCOD
1) ΔCOD = ΔBOA (вертик.) ; 2) ) AO = OC (по условию); 3) BO = OD (по условию)
⇒ ΔAOB = ΔCOD (по 1-му признаку равенства Δ)
∠3= ∠4 ( н/л при прямых CD и AB и секущей AC ) ⇒ CD ∥ AB
То BC ∥ AD ; CD ∥ AB ⇒АВСD – параллелограмм
Слайд 10Признаки параллелограмма
3)Если в четырехугольнике одна пара сторон равна и параллельна,
то этот четырехугольник- параллелограмм
Дано:
ABCD – четырехугольник
AB = CD, AB ∥ CD
Доказать :
АВСD – параллелограмм
Доказательство:
Рассмотрим ΔADB и ΔCDB :
BD - общая ; 2) AB = CD (по условию) ; 3) ∠1 = ∠2 ( н/л при прямых CD и AB и секущей BD)
⇒ ΔADB = ΔCDB (по 1 признаку равенства Δ)
∠3= ∠4 ( н/л при прямых BC и AD и секущей BD) ⇒ BC∥ AD
⇒АВСD – параллелограмм
Дано:
ABCD – четырехугольник
AB = CD, AB ∥ CD
Доказать :
АВСD – параллелограмм
Доказательство:
Рассмотрим ΔADB и ΔCDB :
BD - общая ; 2) AB = CD (по условию) ; 3) ∠1 = ∠2 ( н/л при прямых CD и AB и секущей BD)
⇒ ΔADB = ΔCDB (по 1 признаку равенства Δ)
∠3= ∠4 ( н/л при прямых BC и AD и секущей BD) ⇒ BC∥ AD
⇒АВСD – параллелограмм
Слайд 11Площади параллелограмма
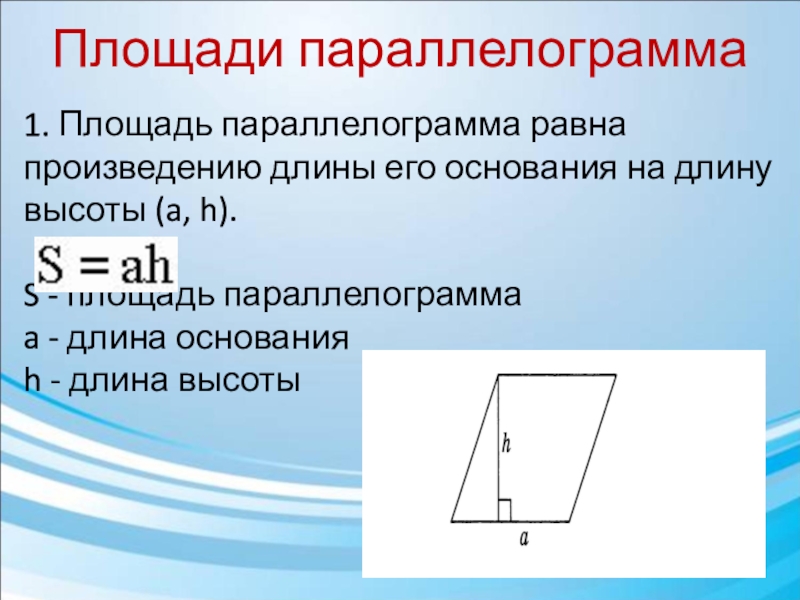
1. Площадь параллелограмма равна произведению длины его основания на
длину высоты (a, h).
S - площадь параллелограмма
a - длина основания
h - длина высоты
S - площадь параллелограмма
a - длина основания
h - длина высоты
Слайд 12Площади параллелограмма
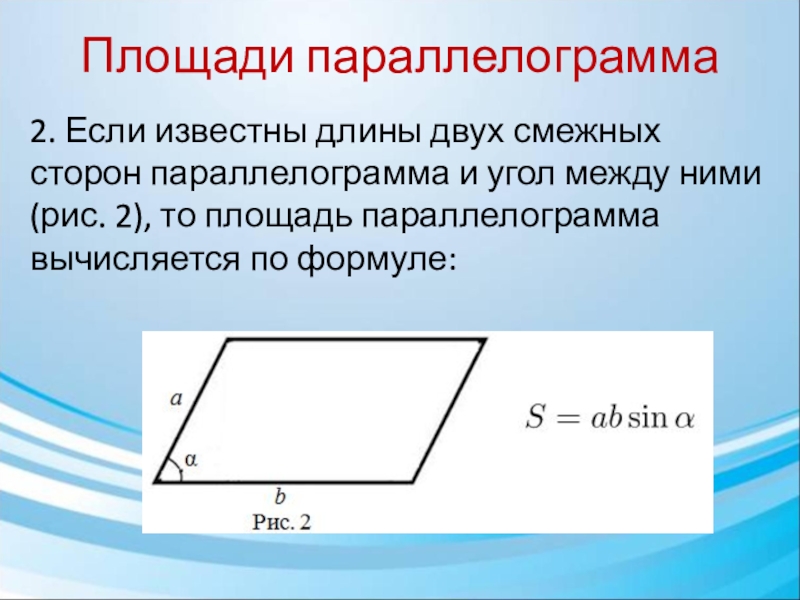
2. Если известны длины двух смежных сторон параллелограмма и угол
между ними (рис. 2), то площадь параллелограмма вычисляется по формуле:
Слайд 13Площади параллелограмма
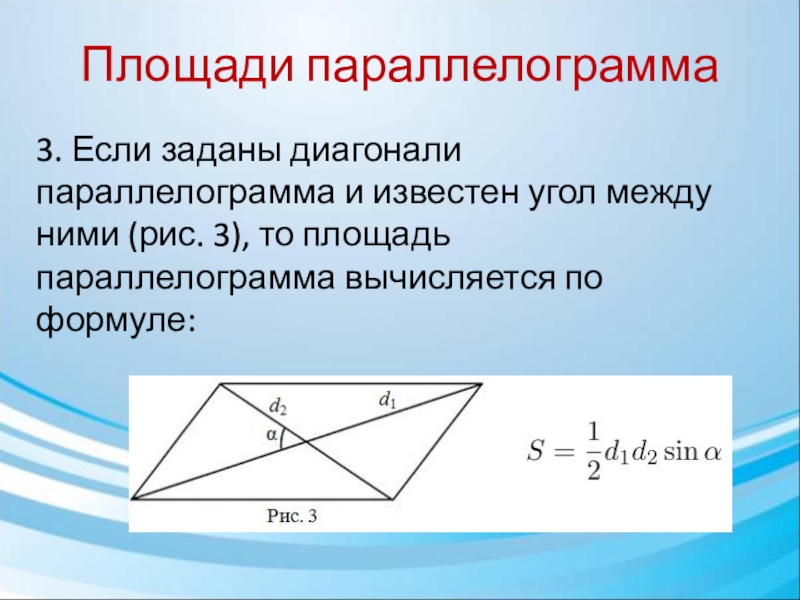
3. Если заданы диагонали параллелограмма и известен угол между ними
(рис. 3), то площадь параллелограмма вычисляется по формуле:
Слайд 14Периметр параллелограмма
Периметр параллелограмма равен удвоенной сумме 2-х его смежных сторон
(a, b).
P - периметр параллелограмм
a - длина 1-ой стороны параллелограмма
b - длина 2-ой стороны параллелограмма
P - периметр параллелограмм
a - длина 1-ой стороны параллелограмма
b - длина 2-ой стороны параллелограмма
Слайд 19Решение задач
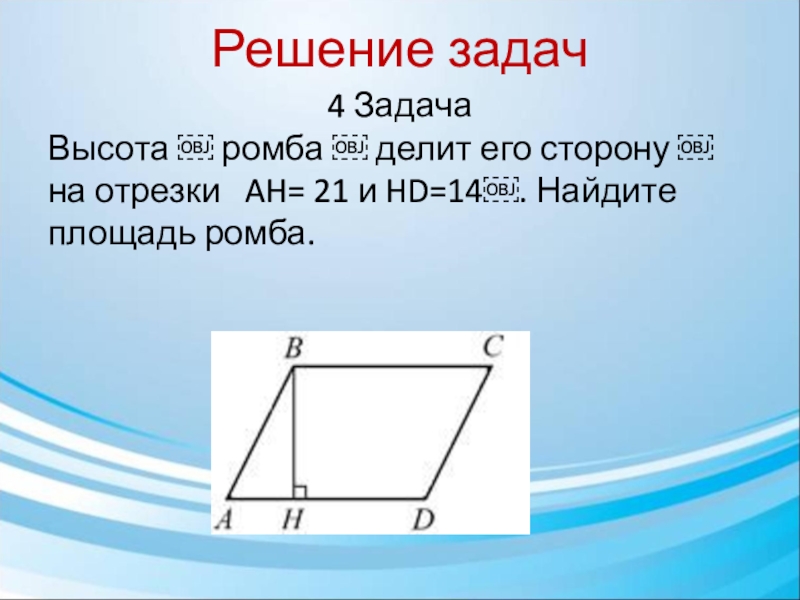
4 Задача
Высота  ромба  делит его сторону  на
отрезки AH= 21 и HD=14. Найдите площадь ромба.
Слайд 20Решение задач
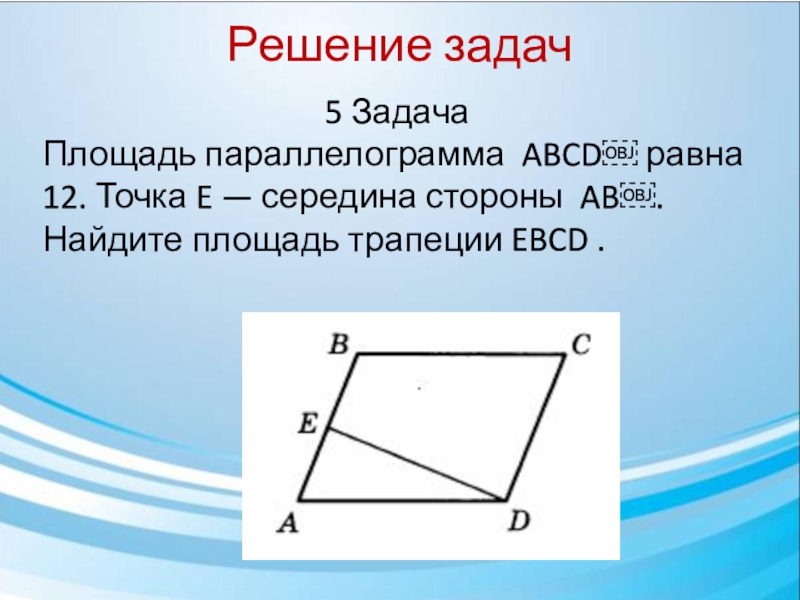
5 Задача
Площадь параллелограмма ABCD равна 12. Точка E —
середина стороны AB. Найдите площадь трапеции EBCD .
Слайд 21Решение задач
6 Задача
Периметр параллелограмма АВСD равен 50,
∠ С
= 30°,а перпендикуляр к стороне АD= 6,5 см. Найдите стороны параллелограмма.
Дано:
АBCD – параллелограмм
Р ABCD= 50 см.
∠ С = 30°
Найти :
АB, ВС, СD, АD.
Дано:
АBCD – параллелограмм
Р ABCD= 50 см.
∠ С = 30°
Найти :
АB, ВС, СD, АD.
Слайд 22Решение задач
7 Задача
Периметр ромба равен 116, а один
из углов равен 30°. Найдите площадь ромба.
Слайд 23Решение задач
8 Задача
Дано: АВСD- параллелограмм
Биссектриса ∠В пересекает сторону АD
АМ=8
см, МD= 4 см
Найти: PABCD
Найти: PABCD
Слайд 24Решение задач
9 Задача
Дано: АВСD- параллелограмм
PABCD=32см
AB:CD= 3:1
Найти наибольшую
сторону т.е.
АВ
Слайд 25Решение задач
10 Задача
Периметр параллелограмма ABCD равен 10 см. Найдите
длину диагонали BD, зная, что периметр треугольника ABD равен 8 см.
Слайд 26Решение
1 Задача
1)ABCD - параллелограмм ⇒ ∠А = ∠С и ∠В
= ∠D
(по свойству параллелограмма)
2) ∠А = ∠С = 84°
3) ∠А + ∠В = 180° (односторонние) ⇒ ∠В = 180°- 84°= =96° ⇒ ∠В = ∠D = 96°
Ответ: ∠С = 84°; ∠В = 96°; ∠D = 96°
(по свойству параллелограмма)
2) ∠А = ∠С = 84°
3) ∠А + ∠В = 180° (односторонние) ⇒ ∠В = 180°- 84°= =96° ⇒ ∠В = ∠D = 96°
Ответ: ∠С = 84°; ∠В = 96°; ∠D = 96°
Слайд 27Решение
2 Задача
1)Т.к. ∠A + ∠B + ∠C + ∠D =
360° ⇒
∠ D = 360°- 237°= 123°
2) ∠D = ∠B = 123°
Ответ: ∠В = 123°
∠ D = 360°- 237°= 123°
2) ∠D = ∠B = 123°
Ответ: ∠В = 123°
Слайд 28Решение
3 Задача
1)ABCD - параллелограмм ⇒ ∠А = ∠С и ∠В
= ∠D
(по свойству параллелограмма)
2)Рассмотрим треугольник ACD:
∠АCD + ∠СDA + ∠DAC = 180° ⇒ ∠СDA = 180°- (37°+ 16°) = 127° ⇒ ∠В = ∠D = 127°
3) ∠А + ∠В – односторонние ⇒ ∠А = 180°- 127°= 53°
∠А = ∠С = 53°
Ответ: ∠А =53°; ∠В = 127° ∠С = 53°; ∠D = 127°
(по свойству параллелограмма)
2)Рассмотрим треугольник ACD:
∠АCD + ∠СDA + ∠DAC = 180° ⇒ ∠СDA = 180°- (37°+ 16°) = 127° ⇒ ∠В = ∠D = 127°
3) ∠А + ∠В – односторонние ⇒ ∠А = 180°- 127°= 53°
∠А = ∠С = 53°
Ответ: ∠А =53°; ∠В = 127° ∠С = 53°; ∠D = 127°
Слайд 29Решение
4 Задача
Из прямоугольного треугольника  найдём 
BH=√AB²-AH²= √AD²- AH²= √
(AH+HD) ²- AH²= √1225-441= 28
Площадь ромба можно найти как произведение основания на высоту:
S= AD* BH= 35*28= 980
Ответ: 980.
Площадь ромба можно найти как произведение основания на высоту:
S= AD* BH= 35*28= 980
Ответ: 980.
Слайд 30Решение
5 Задача
Диагональ параллелограмма делит его на два равных треугольника, поэтому
SABD= 6. Медиана треугольника делит его на два равновеликих треугольника, поэтому SADE= ½ SACD.
Следовательно,
SEBCD=SABCD- SADE=12-3=9
Ответ: 9
Следовательно,
SEBCD=SABCD- SADE=12-3=9
Ответ: 9
Слайд 31Решение
6 Задача
Проведём высоту BH.
Треугольник AHB – прямоугольный. Угол A равен
углу C и равен 300(по свойству о противоположных углах в параллелограмме). 2BH=AB (по свойству катета, лежащего напротив угла в 300 в прямоугольном треугольнике). Значит AB = 13 см.
AB = CD, BC = AD (по свойству противоположных сторон в параллелограмме) Значит AB=CD=13см. Так как периметр параллелограмма равен 50 см, то BC=AD=(50 – 26):2=12см.
Ответ: AB = CD = 13 см, BC = AD = 12 см.
AB = CD, BC = AD (по свойству противоположных сторон в параллелограмме) Значит AB=CD=13см. Так как периметр параллелограмма равен 50 см, то BC=AD=(50 – 26):2=12см.
Ответ: AB = CD = 13 см, BC = AD = 12 см.
Слайд 32Решение
7 Задача
Решение: Обозначим CD за x, тогда АВ- 3x
Можем составить уравнение:
P= 2*3x+ 2*x
32= 6x+2x
32=8x
x=4
То сторона АВ= 3*4=12 cм
Ответ: 12см
Слайд 33Решение
8 Задача
AD= AM+MD= 8+4 =12
AD ∥ BC и AD=BC
⇒ BC=12 см
∠MBC= ∠BMA (т.к. н/л при прямых BC и AD и секущей BM)
Δ ABM – р/б ⇒ AM= AB =CD= 8см
PABCD= 12+12+8+8=40
Ответ: PABCD=40 см
∠MBC= ∠BMA (т.к. н/л при прямых BC и AD и секущей BM)
Δ ABM – р/б ⇒ AM= AB =CD= 8см
PABCD= 12+12+8+8=40
Ответ: PABCD=40 см
Слайд 34Решение
9 Задача
Проведём высоту в ромбе и введём обозначения как
показано на рисунке. Все стороны ромба равны, поэтому AB= P/4 =116/4= 29  Найдём BH из прямоугольного треугольника ABH:
BH= AB*sin30= 29 * ½= 14,5
Найдём площадь ромба как произведение стороны на высоту:
S= AD*BH= 29* 14,5= 420,5
Ответ: 420,5.
BH= AB*sin30= 29 * ½= 14,5
Найдём площадь ромба как произведение стороны на высоту:
S= AD*BH= 29* 14,5= 420,5
Ответ: 420,5.
Слайд 35Решение
10 Задача
РABCD= 2*(AB+AD), поэтому AB+ AD= ½PABCD=1/2 *10= 5 см
PABCD=AB+AD+BD=8см
Откуда BD=8 см –( AB+AD)= 8см – 5 см = 3см
Ответ: 3 см