50 города Макеевки»
Малышко Дарья
ученица 10 класса
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по теме Параллельность прямых, параллельность прямой и плоскости, параллельность плоскостей(Геометрия 10 класс)
Содержание
- 1. Презентация по теме Параллельность прямых, параллельность прямой и плоскости, параллельность плоскостей(Геометрия 10 класс)
- 2. ВСПОМНИМ ПЛАНИМЕТРИЮКаково может быть взаимное расположение двух прямых на плоскости?Какие прямые в планиметрии называются параллельными?
- 3. ВСПОМНИМ ПЛАНИМЕТРИЮАксиома параллельных прямых - ?Через точку,
- 4. ВСПОМНИМ ПЛАНИМЕТРИЮСледствия аксиомы параллельных прямых - ?Если
- 5. Стереометрия.Параллельность в пространстве.
- 6. Скрещивающиеся прямые.Прямые, которые не лежат в одной
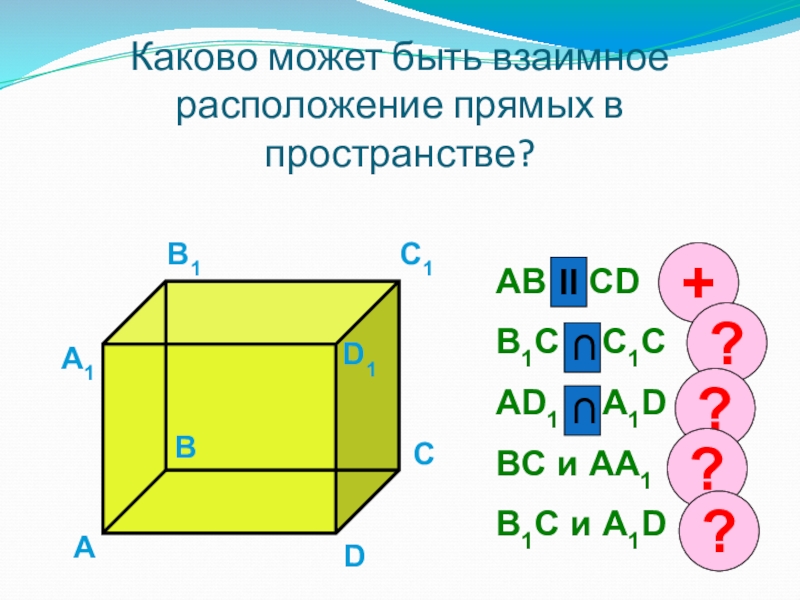
- 7. Каково может быть взаимное расположение прямых в
- 8. Какие прямые в пространстве называются параллельными?АBCDА1B1C1D1B1C и
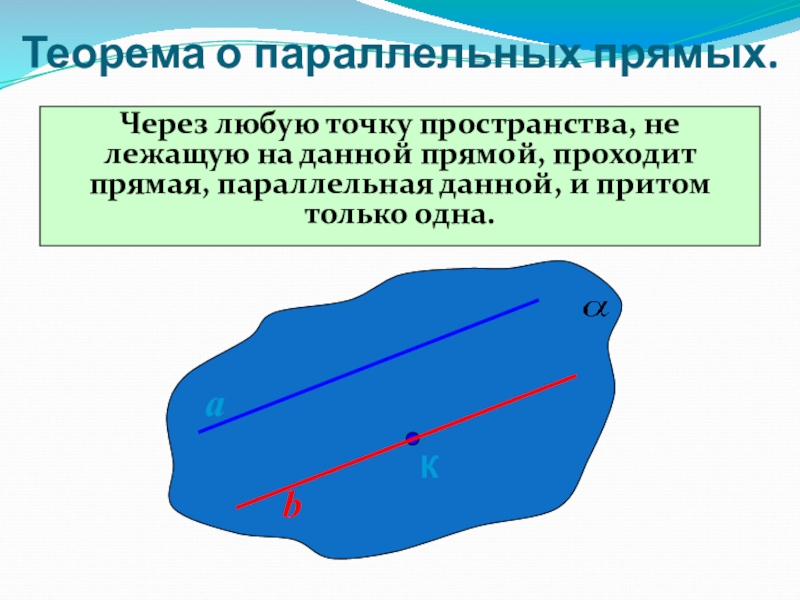
- 9. Теорема о параллельных прямых.Через любую точку пространства,
- 10. …они лежат на параллельных прямыхОтрезки в пространстве
- 11. Теорема о параллельности трех прямых в пространстве.Если две прямые параллельны третьей прямой, то они параллельныabсДано:Доказать:и
- 12. Параллельность прямой и плоскости.Прямая и плоскость называются
- 13. Параллельные плоскости.Две плоскости называются параллельными, если они
- 14. Свойства параллельных плоскостей.Если две параллельные плоскости пересекаются
- 15. Справедливо ли утверждение: а) Если прямая, лежащая
- 16. Ответьте на вопросы А) Прямая параллельна плоскости.
- 17. Справедливы ли утверждения:А) если прямая одной плоскости
- 18. Каким может быть взаимное расположение…плоскостей α и
- 19. Каково может быть взаимное расположение…плоскостей α и
- 20. Назовите прямые, проходящие через вершины куба A…D1 и параллельные прямой AC.Ответ: A1C1.
- 21. Сколько имеется пар параллельных прямых, содержащих ребра
- 22. Являются ли параллельными прямые AB и CD, проходящие через вершины тетраэдра ABCD?Ответ: Нет.
- 23. Сколько имеется пар параллельных прямых, содержащих ребра
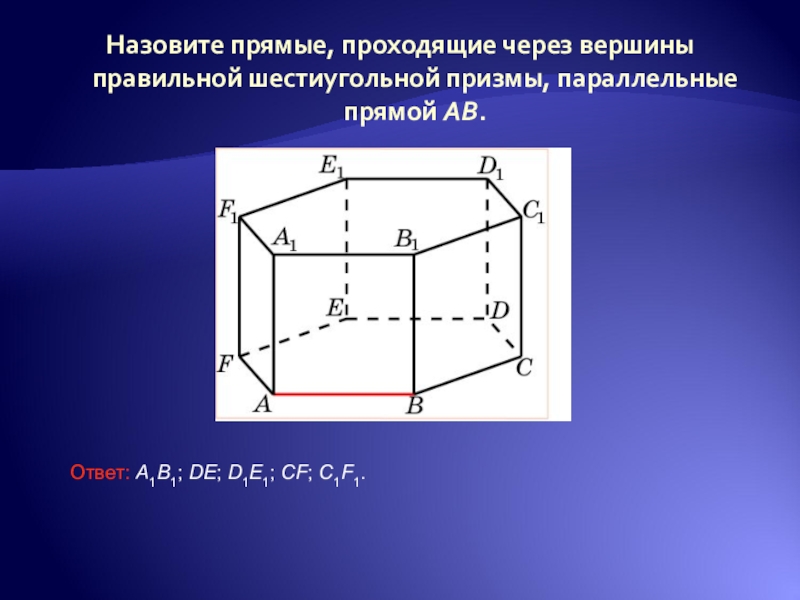
- 24. Назовите прямые, проходящие через вершины правильной шестиугольной призмы, параллельные прямой AB.Ответ: A1B1; DE; D1E1; CF; C1F1.
- 25. Сколько имеется пар параллельных прямых, содержащих ребра
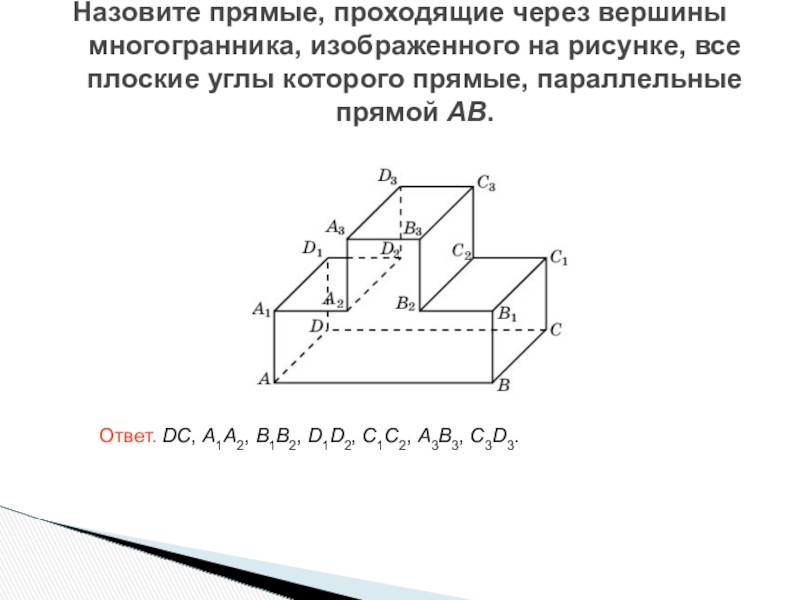
- 26. Назовите прямые, проходящие через вершины многогранника, изображенного
- 27. Сколько имеется пар параллельных прямых, содержащих ребра
- 28. Сколько имеется пар параллельных прямых, содержащих ребра
- 29. В пространстве даны n параллельных между собой
- 30. Практическая работа KMDMNKОбозначьте самостоятельно фигуру.Обозначьте самостоятельно фигуру.I вариантII вариант
- 31. Материалы для презентации взяты из открытых источников Интернета
ВСПОМНИМ ПЛАНИМЕТРИЮКаково может быть взаимное расположение двух прямых на плоскости?Какие прямые в планиметрии называются параллельными?
Слайд 2ВСПОМНИМ ПЛАНИМЕТРИЮ
Каково может быть взаимное расположение двух прямых на плоскости?
Какие прямые
в планиметрии называются параллельными?
Слайд 3
ВСПОМНИМ ПЛАНИМЕТРИЮ
Аксиома параллельных прямых - ?
Через точку, не лежащую на данной
прямой,
проходит прямая, параллельная данной и притом только одна
Слайд 4
ВСПОМНИМ ПЛАНИМЕТРИЮ
Следствия аксиомы параллельных прямых - ?
Если прямая пересекает одну из
параллельных прямых, то она пересекает и другую.
Если две прямые параллельны третьей прямой, то они параллельны.
Слайд 6Скрещивающиеся прямые.
Прямые, которые не лежат в одной плоскости и не пересекаются,
называются скрещивающимися.
Углом между скрещивающимися прямыми называется угол между пересекающимися параллельными им прямыми.
Общим перпендикуляром двух скрещивающихся прямых называется отрезок с концами на этих прямых, являющийся перпендикуляром к каждой из них.
Расстоянием между скрещивающимися прямыми называется длина их общего перпендикуляра.
Углом между скрещивающимися прямыми называется угол между пересекающимися параллельными им прямыми.
Общим перпендикуляром двух скрещивающихся прямых называется отрезок с концами на этих прямых, являющийся перпендикуляром к каждой из них.
Расстоянием между скрещивающимися прямыми называется длина их общего перпендикуляра.
Слайд 7Каково может быть взаимное расположение прямых в пространстве?
А
B
C
D
А1
B1
C1
D1
AB и CD
B1C и
C1C
AD1 и A1D
BC и AA1
B1C и A1D
AD1 и A1D
BC и AA1
B1C и A1D
II
+
∩
?
∩
?
?
?
Слайд 8Какие прямые в пространстве называются параллельными?
А
B
C
D
А1
B1
C1
D1
B1C и A1D
AB и СD
Параллельными
называются
прямые,
лежащие в одной
плоскости и не
имеющие точек
пересечения.
лежащие в одной
плоскости и не
имеющие точек
пересечения.
Слайд 9
Теорема о параллельных прямых.
Через любую точку пространства, не лежащую на данной
прямой, проходит прямая, параллельная данной, и притом только одна.
К
a
b
Слайд 10…они лежат на параллельных прямых
Отрезки в пространстве называются параллельными, если …
Лучи
в пространстве называются параллельными, если …
Параллельные отрезки,
параллельные лучи
в пространстве.
Слайд 11Теорема о параллельности трех прямых в пространстве.
Если две прямые параллельны третьей
прямой, то они параллельны
a
b
с
Дано:
Доказать:
и
Слайд 12Параллельность прямой и плоскости.
Прямая и плоскость называются параллельными ,если они не
пересекаются, т. е. не имеют общих точек.
Если прямая, не принадлежащая плоскости, параллельна какой-нибудь прямой в этой плоскости, то она параллельна и самой плоскости.
Если прямая, не принадлежащая плоскости, параллельна какой-нибудь прямой в этой плоскости, то она параллельна и самой плоскости.
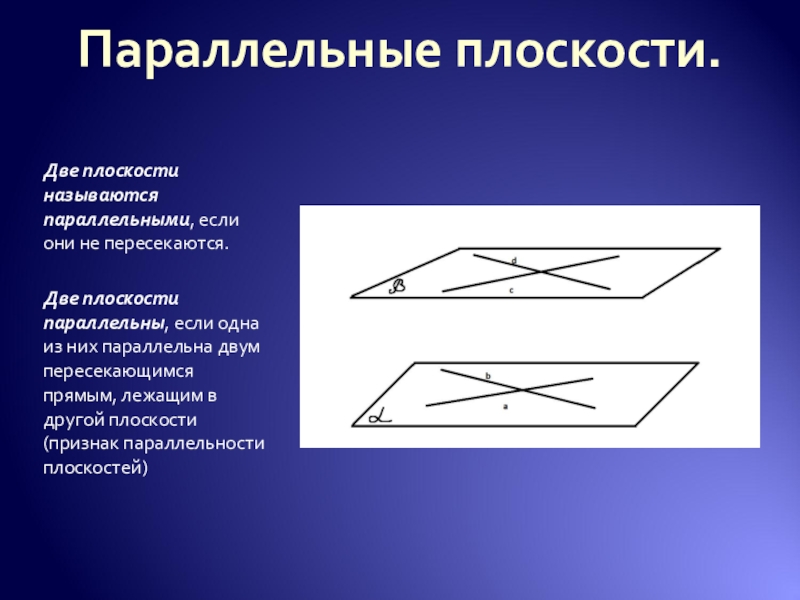
Слайд 13Параллельные плоскости.
Две плоскости называются параллельными, если они не пересекаются.
Две плоскости параллельны,
если одна из них параллельна двум пересекающимся прямым, лежащим в другой плоскости (признак параллельности плоскостей)
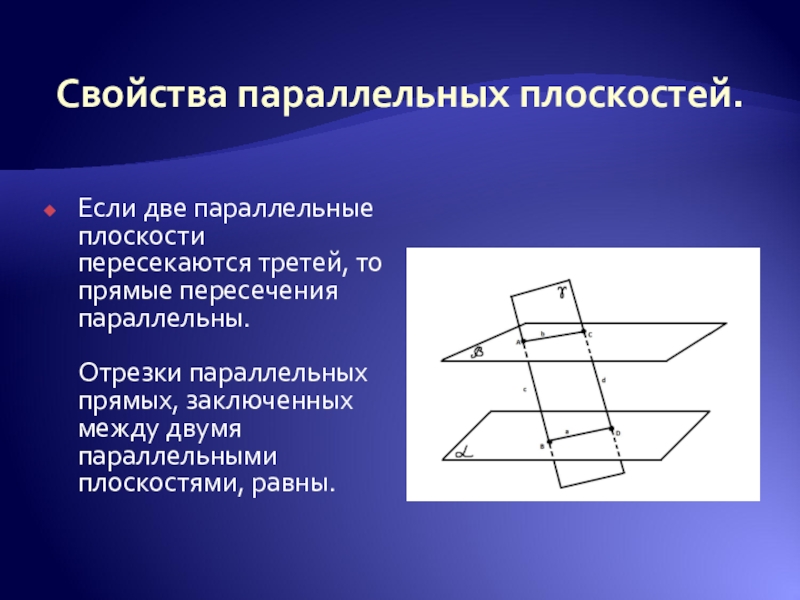
Слайд 14Свойства параллельных плоскостей.
Если две параллельные плоскости пересекаются третей, то прямые пересечения
параллельны.
Отрезки параллельных прямых, заключенных между двумя параллельными плоскостями, равны.
Слайд 15Справедливо ли утверждение:
а) Если прямая, лежащая вне плоскости, скрещивается с прямой,
лежащей в плоскости, то первая прямая параллельна плоскости
б) Если прямая а пересекает прямую b и пересекает плоскость α, то b может быть параллельна α.
Да, нет.
Нет, да.
Да, да.
Нет, нет.
б) Если прямая а пересекает прямую b и пересекает плоскость α, то b может быть параллельна α.
Да, нет.
Нет, да.
Да, да.
Нет, нет.
Слайд 16Ответьте на вопросы
А) Прямая параллельна плоскости. Как она может быть расположена
по отношению к прямой, лежащей в этой плоскости?
Б) Каждая из двух прямых а и b параллельна плоскости. Каким может быть взаимное расположение a и б ?
А) параллельна; Б) пересекаются, параллельны
А) параллельна, скрещивающаяся;Б) пересекаются, параллельны
А) параллельна, скрещивающаяся; Б) пересекаются
А) скрещивающаяся, пересекает; Б) пересекаются, параллельны
Б) Каждая из двух прямых а и b параллельна плоскости. Каким может быть взаимное расположение a и б ?
А) параллельна; Б) пересекаются, параллельны
А) параллельна, скрещивающаяся;Б) пересекаются, параллельны
А) параллельна, скрещивающаяся; Б) пересекаются
А) скрещивающаяся, пересекает; Б) пересекаются, параллельны
Слайд 17Справедливы ли утверждения:
А) если прямая одной плоскости параллельна прямой другой плоскости,
то плоскости параллельны.
Б) если две прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то плоскости параллельны
Нет, да.
Да, нет.
Да, да.
Нет, нет.
Б) если две прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то плоскости параллельны
Нет, да.
Да, нет.
Да, да.
Нет, нет.
Слайд 18Каким может быть взаимное расположение…
плоскостей α и β, если известно, что:
Некоторая
прямая а лежит в α и не лежит в β.
Только пересекаться.
Только быть параллельными.
Могут и пересекаться и быть параллельными.
прямая а лежит в α и не лежит в β.
Только пересекаться.
Только быть параллельными.
Могут и пересекаться и быть параллельными.
Слайд 19Каково может быть взаимное расположение…
плоскостей α и β, если прямая а:
пересекает α и
параллельна β?
Только пересекаться.
Только быть параллельными.
Могут и пересекаться и быть параллельными.
параллельна β?
Только пересекаться.
Только быть параллельными.
Могут и пересекаться и быть параллельными.
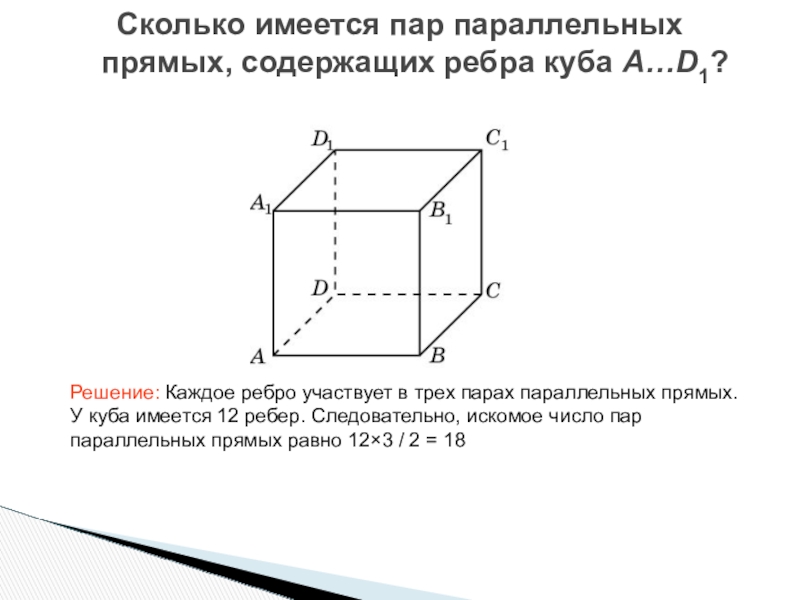
Слайд 21Сколько имеется пар параллельных прямых, содержащих ребра куба A…D1?
Решение: Каждое ребро
участвует в трех парах параллельных прямых. У куба имеется 12 ребер. Следовательно, искомое число пар параллельных прямых равно 12×3 / 2 = 18
Слайд 22Являются ли параллельными прямые AB и CD, проходящие через вершины тетраэдра
ABCD?
Ответ: Нет.
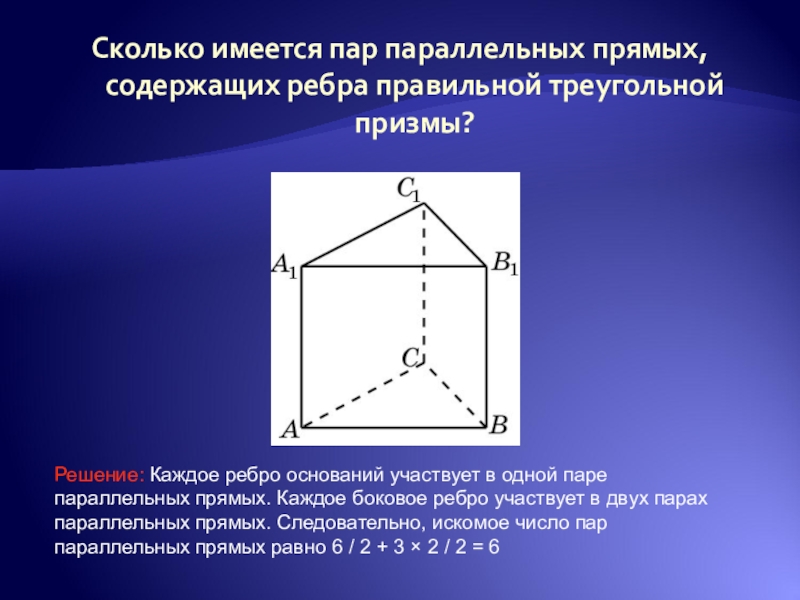
Слайд 23Сколько имеется пар параллельных прямых, содержащих ребра правильной треугольной призмы?
Решение: Каждое
ребро оснований участвует в одной паре параллельных прямых. Каждое боковое ребро участвует в двух парах параллельных прямых. Следовательно, искомое число пар параллельных прямых равно 6 / 2 + 3 × 2 / 2 = 6
Слайд 24Назовите прямые, проходящие через вершины правильной шестиугольной призмы, параллельные прямой AB.
Ответ:
A1B1; DE; D1E1; CF; C1F1.
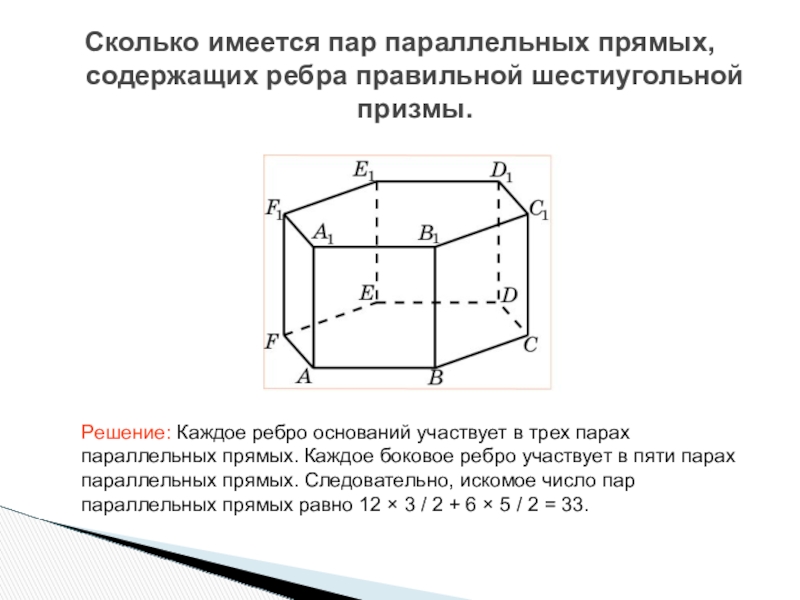
Слайд 25Сколько имеется пар параллельных прямых, содержащих ребра правильной шестиугольной призмы.
Решение:
Каждое ребро оснований участвует в трех парах параллельных прямых. Каждое боковое ребро участвует в пяти парах параллельных прямых. Следовательно, искомое число пар параллельных прямых равно 12 × 3 / 2 + 6 × 5 / 2 = 33.
Слайд 26Назовите прямые, проходящие через вершины многогранника, изображенного на рисунке, все плоские
углы которого прямые, параллельные прямой AB.
Ответ. DC, A1A2, B1B2, D1D2, C1C2, A3B3, C3D3.
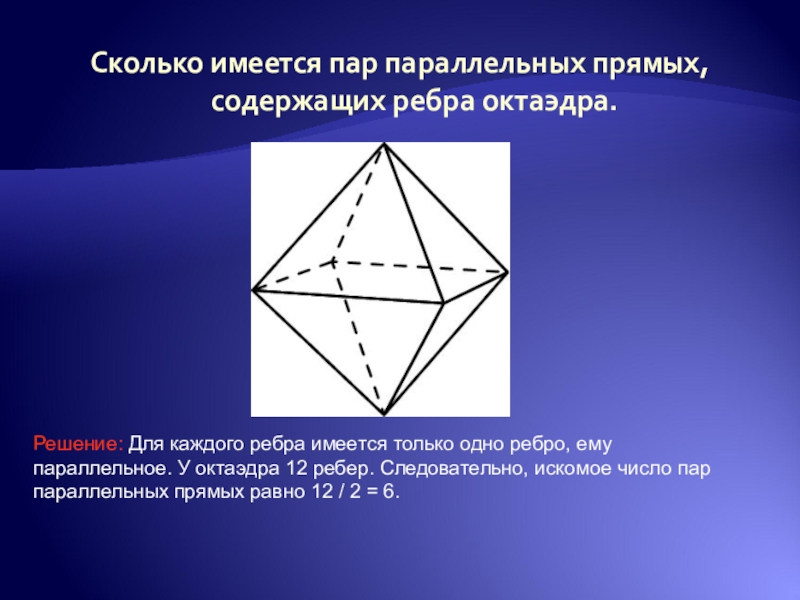
Слайд 27Сколько имеется пар параллельных прямых, содержащих ребра октаэдра.
Решение: Для каждого
ребра имеется только одно ребро, ему параллельное. У октаэдра 12 ребер. Следовательно, искомое число пар параллельных прямых равно 12 / 2 = 6.
Слайд 28Сколько имеется пар параллельных прямых, содержащих ребра икосаэдра.
Решение: Для каждого
ребра имеется только одно ребро, ему параллельное. У икосаэдра 30 ребер. Следовательно, искомое число пар параллельных прямых равно 30 / 2 = 15.
Слайд 29В пространстве даны n параллельных между собой прямых. Сколько плоскостей можно
провести через различные пары этих прямых, если известно, что никакие три из них не лежат в одной плоскости?
Ответ: n (n – 1) / 2
Слайд 30Практическая работа
K
M
D
M
N
K
Обозначьте самостоятельно фигуру.
Обозначьте самостоятельно фигуру.
I вариант
II вариант
