- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по теме Основные понятия стереометрии(1 урок)-10 класс
Содержание
- 1. Презентация по теме Основные понятия стереометрии(1 урок)-10 класс
- 2. ПЛАНИМЕТРИЯСТЕРЕОМЕТРИЯГЕОМЕТРИЯ на плоскостиГЕОМЕТРИЯ в пространстве«планиметрия» – наименование смешанного
- 3. Изучая СТЕРЕОМЕТРИЮ Мы проведем систематическое рассмотрение свойств
- 4. ГЕОМЕТРИЯ возникла из практических задач людей;ГЕОМЕТРИЯ лежит
- 5. Интуитивное, живое пространственное воображение в сочетании со
- 6. Учебный материал Что будем изучать
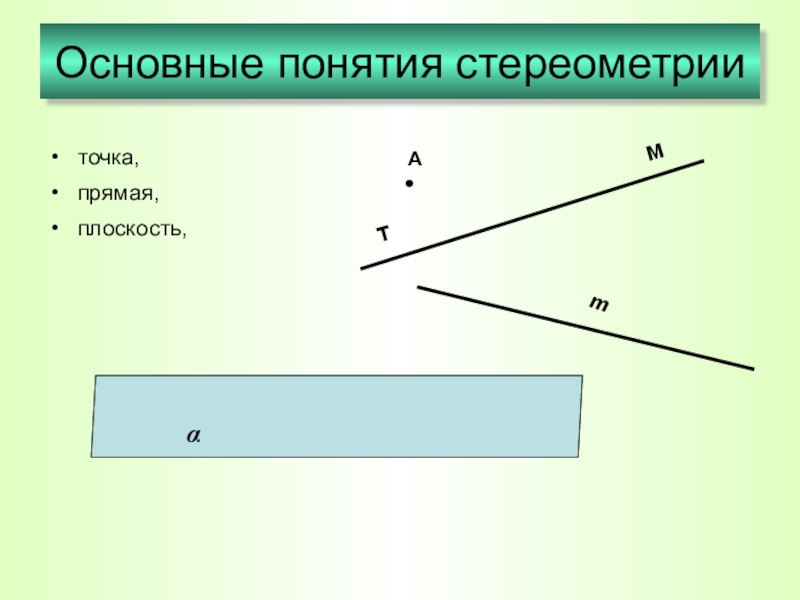
- 7. Основные понятия стереометрии точка,прямая,плоскость,
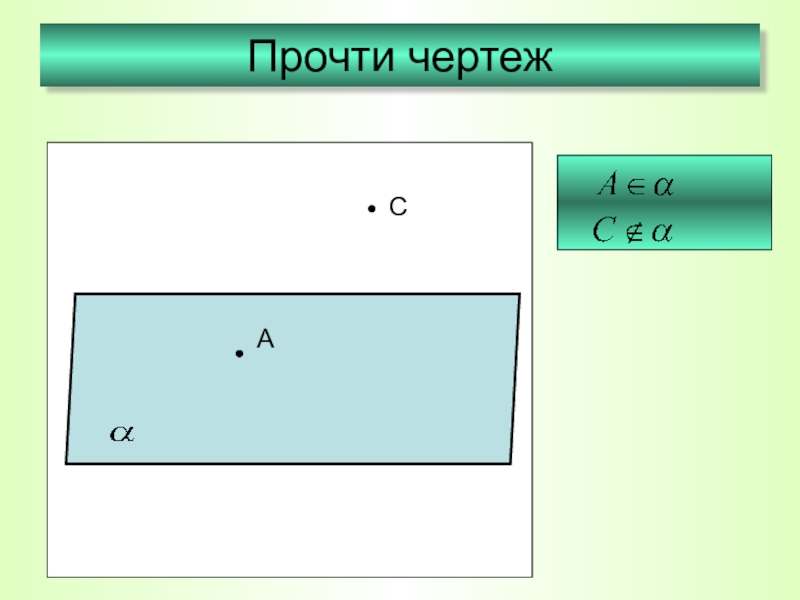
- 8. Прочти чертежAС
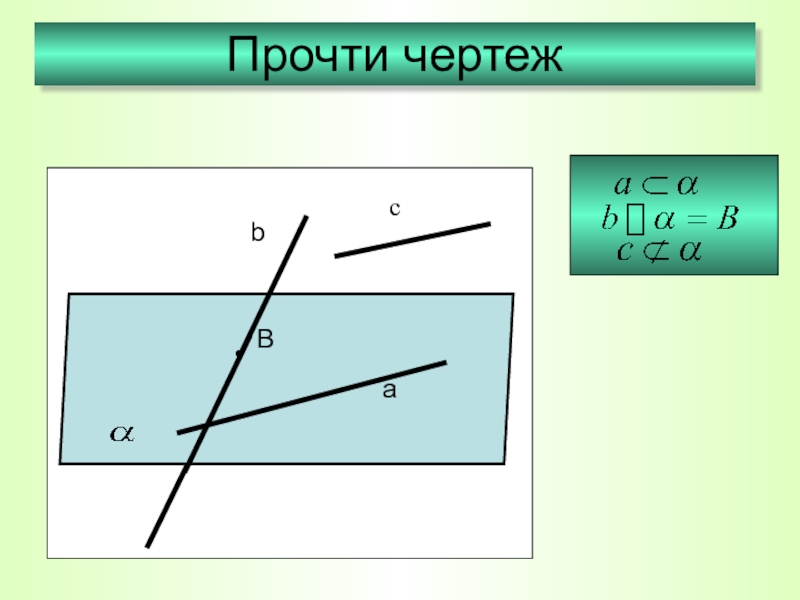
- 9. Прочти чертежBcba
- 10. Прочти чертеж
- 11. Аксиомы стереометрииСлово «аксиома» греческого происхождения и в
- 12. Аксиомы стереометрииА-1Какова бы ни была плоскость, существуют
- 13. Аксиомы стереометрииА-2Если две точки прямой лежат в
- 14. Аксиомы стереометрииА-3Если две плоскости имеют общую точку,
- 15. СЛЕДСТВИЯ ИЗ АКСИОМТ-1Через любую прямую и не
- 16. СЛЕДСТВИЯ ИЗ АКСИОМТ-2Через любые две пересекающиеся прямые
- 17. По трем точкам, не лежащим на одной
- 18. Любые три точки лежат в одной плоскости.Любые
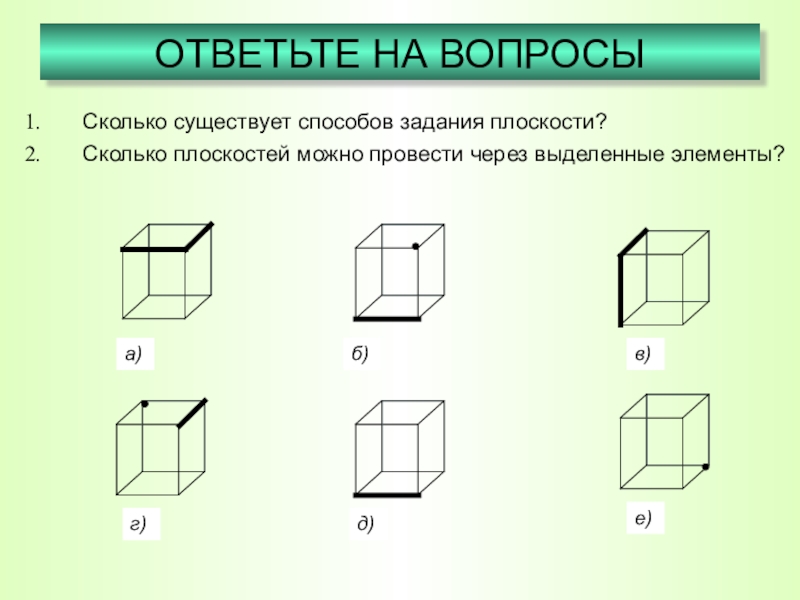
- 19. Сколько существует способов задания плоскости?Сколько плоскостей можно провести через выделенные элементы?ОТВЕТЬТЕ НА ВОПРОСЫ а)б)в)г)д)е)
- 20. « СЧИТАЙ НЕСЧАСТНЫМ ТОТ ДЕНЬ ИЛИ ЧАС,
- 21. СПАСИБО ЗА УРОК!
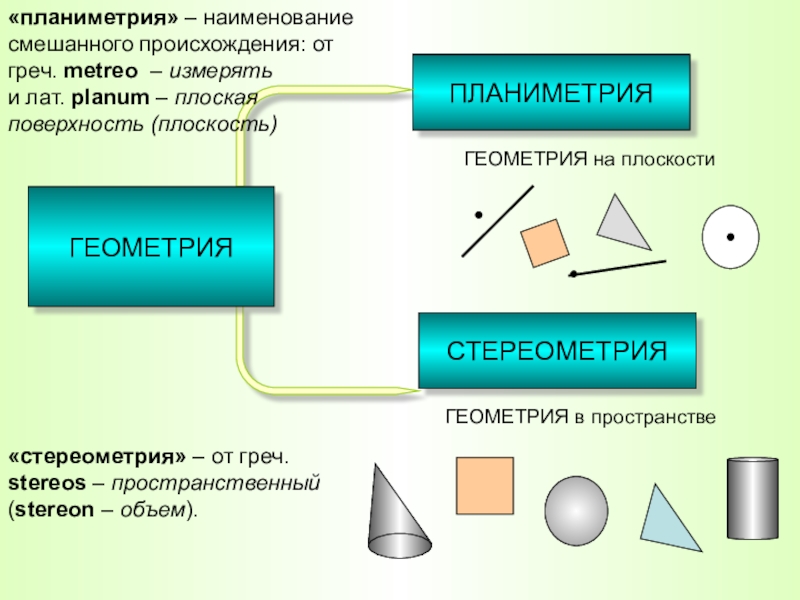
Слайд 2ПЛАНИМЕТРИЯ
СТЕРЕОМЕТРИЯ
ГЕОМЕТРИЯ на плоскости
ГЕОМЕТРИЯ в пространстве
«планиметрия» – наименование смешанного происхождения: от греч. metreo
«стереометрия» – от греч. stereos – пространственный (stereon – объем).
ГЕОМЕТРИЯ
Слайд 3Изучая СТЕРЕОМЕТРИЮ
Мы проведем систематическое рассмотрение
свойств геометрических тел в пространстве.
Освоим различные
При этом мы будем развивать пространственное воображение и логическое мышление
Слайд 4ГЕОМЕТРИЯ возникла из практических задач людей;
ГЕОМЕТРИЯ лежит в основе всей техники
ГЕОМЕТРИЯ нужна
технику,
инженеру,
рабочему,
архитектору,
модельеру …
Мы знаем, что
Слайд 5
Интуитивное, живое пространственное воображение в сочетании со строгой логикой мышления —
ВЫВОД:
«Мой карандаш, бывает еще остроумней моей головы»
Леонард Эйлер (1707—1783).
Слайд 11Аксиомы стереометрии
Слово «аксиома» греческого происхождения и в переводе означает истинное, исходное
Система аксиом стереометрии дает описание свойств пространства и основных его элементов
Понятия «точка», «прямая», «плоскость», «расстояние» принимаются без определений: их описание и свойства содержатся в аксиомах
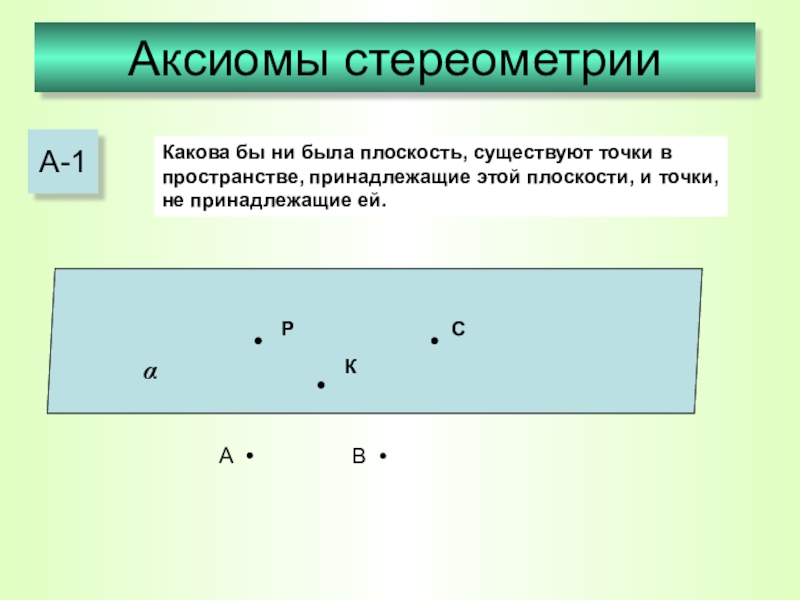
Слайд 12Аксиомы стереометрии
А-1
Какова бы ни была плоскость, существуют точки в пространстве, принадлежащие
А • В •
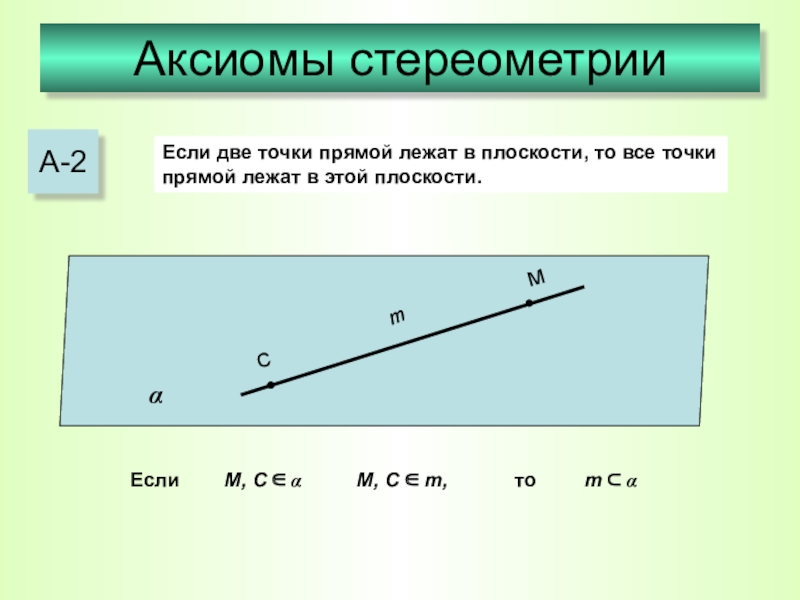
Слайд 13Аксиомы стереометрии
А-2
Если две точки прямой лежат в плоскости, то все точки
m
М, C ∈ α
m ⊂ α
М, C ∈ m,
Если
то
Слайд 14Аксиомы стереометрии
А-3
Если две плоскости имеют общую точку, то они имеют общую
М ∈ α, М ∈ β, М ∈ m
m ⊂ α, m ⊂ β
α ∩ β = m
Слайд 15СЛЕДСТВИЯ ИЗ АКСИОМ
Т-1
Через любую прямую и не принадлежащую ей точку можно
м
А
В
Дано: М∉m
Так как М∉m, то точки А, В и M не принадлежат одной прямой.
По А-1 через точки А, В и M проходит только одна плоскость — плоскость (ABM), Обозначим её α. Прямая m имеет с ней две общие точки — точки A и B, следовательно, по аксиоме А-2 эта прямая лежит в плоскости α..
Таким образом, плоскость α проходит через прямую m и точку M и является искомой.
Докажем, что другой плоскости, проходящей через прямую m и точку M, не существует. Предположим, что есть другая плоскость — β, проходящая через прямую m и точку M. Тогда плоскости α и β проходят через точки А, В и M, не принадлежащие одной прямой, а значит, совпадают. Следовательно, плоскость α единственна.
Теорема доказана
Доказательство
Пусть точки A, B ∈ m.
Слайд 16СЛЕДСТВИЯ ИЗ АКСИОМ
Т-2
Через любые две пересекающиеся прямые можно провести плоскость, и
N
Дано: m ∩ n = M
Доказательство
Отметим на прямой m произвольную точку N, отличную от М.
Рассмотрим плоскость α =(n, N). Так как M∈ α и N∈α, то по А-2 m ⊂ α. Значит обе прямые m, n лежат в плоскости α и следовательно α, является искомой
Докажем единственность плоскости α. Допустим, что есть другая, отличная от плоскости α и проходящая через прямые m и n, плоскость β.
Так как плоскость β проходит через прямую n и не принадлежащую ей точку N, то по T-1 она совпадает с плоскостью α. Единственность плоскости α доказана.
Теорема доказана
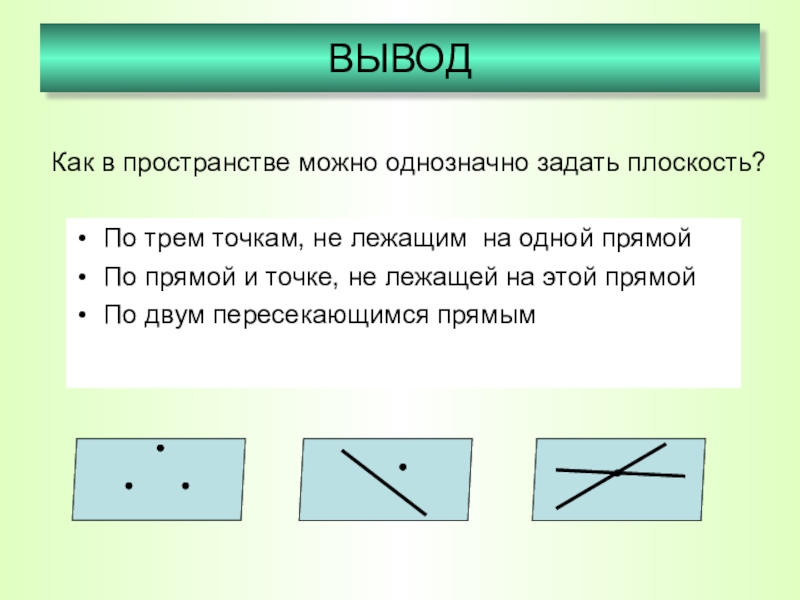
Слайд 17По трем точкам, не лежащим на одной прямой
По прямой и точке,
По двум пересекающимся прямым
ВЫВОД
Как в пространстве можно однозначно задать плоскость?
Слайд 18Любые три точки лежат в одной плоскости.
Любые четыре точки лежат в
Любые четыре точки не лежат в одной плоскости.
Через любые три точки проходит плоскость и при том только одна.
Если прямая пересекает 2 стороны треугольника, то она лежит в плоскости треугольника.
Если прямая проходит через вершину треугольника, то она лежит в плоскости треугольника.
Если прямые не пересекаются, то они параллельны.
Если плоскости не пересекаются, то они параллельны.
В стереометрии мы будем рассматривать ситуации, задающие различные расположения в пространстве основных фигур относительно друг друга
Определите: верно, ли суждение?
ДА
ДА
ДА
НЕТ
НЕТ
НЕТ
НЕТ
НЕТ
Слайд 19Сколько существует способов задания плоскости?
Сколько плоскостей можно провести через выделенные элементы?
ОТВЕТЬТЕ
а)
б)
в)
г)
д)
е)
Слайд 20« СЧИТАЙ НЕСЧАСТНЫМ ТОТ ДЕНЬ ИЛИ ЧАС, В КОТОРЫЙ ТЫ НЕ
Я. А. КОМЕНСКИЙ.