- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по теме: Осевая симметрия (11 класс)
Содержание
- 1. Презентация по теме: Осевая симметрия (11 класс)
- 2. Содержание Симметрия Осевая симметрияСимметрия в геометрии, природе, архитектуре, поэзииЗаключение
- 3. ОпределениеСимметрия (от греч. Symmetria – соразмерность), в
- 4. Осевая симметрияДве точки А и А1 называются
- 5. Фигура называется симметричной относительно прямой a, если
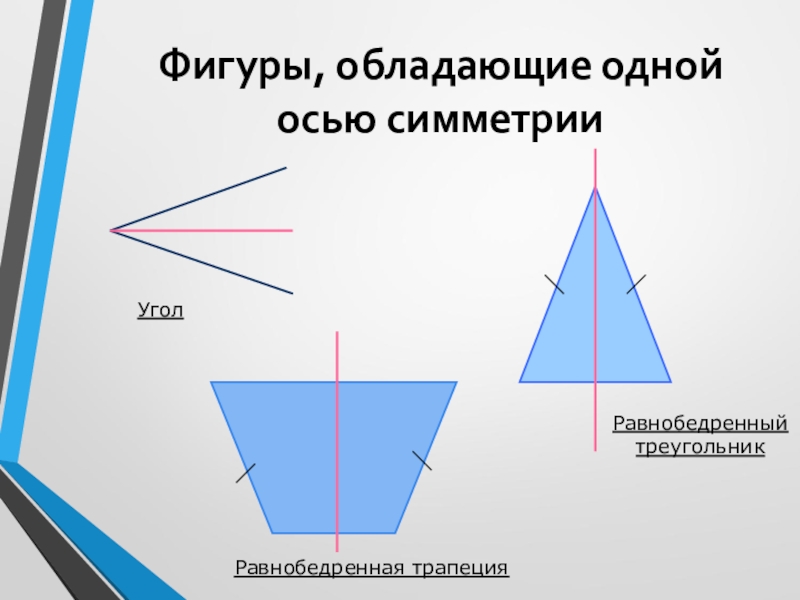
- 6. Фигуры, обладающие одной осью симметрииУголРавнобедренный треугольникРавнобедренная трапеция
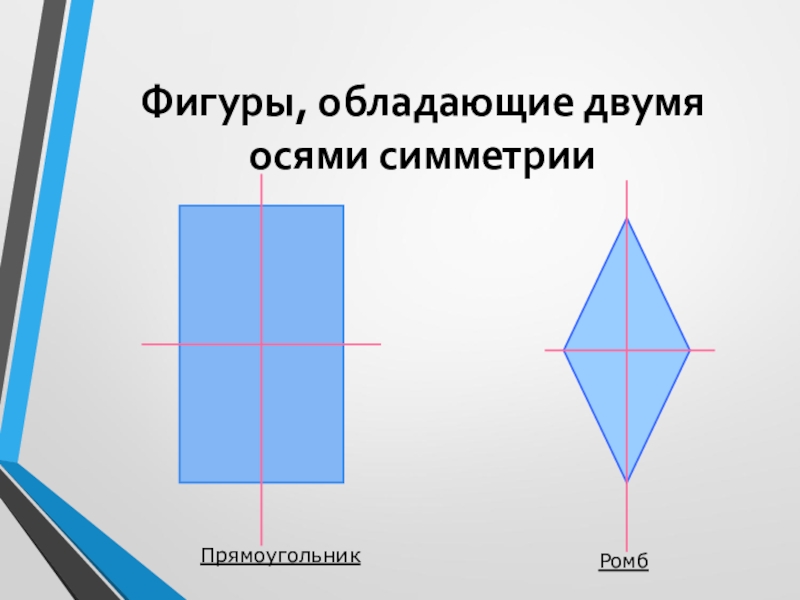
- 7. Фигуры, обладающие двумя осями симметрииПрямоугольникРомб
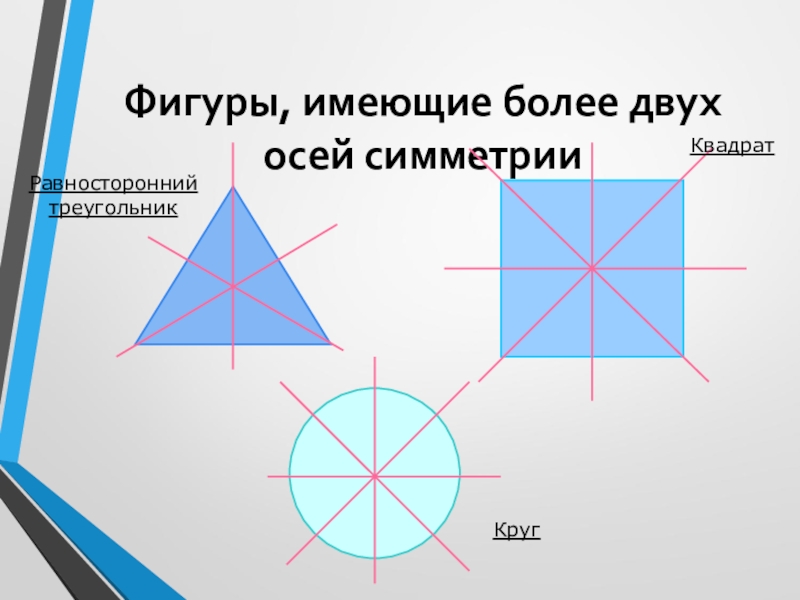
- 8. Фигуры, имеющие более двух осей симметрииРавносторонний треугольникКвадратКруг
- 9. Фигуры, не обладающие осевой симметриейПроизвольный треугольникПараллелограммНеправильный многоугольник
- 10. Построениеточки, симметричной даннойотрезка, симметричного данномутреугольника, симметричного данному
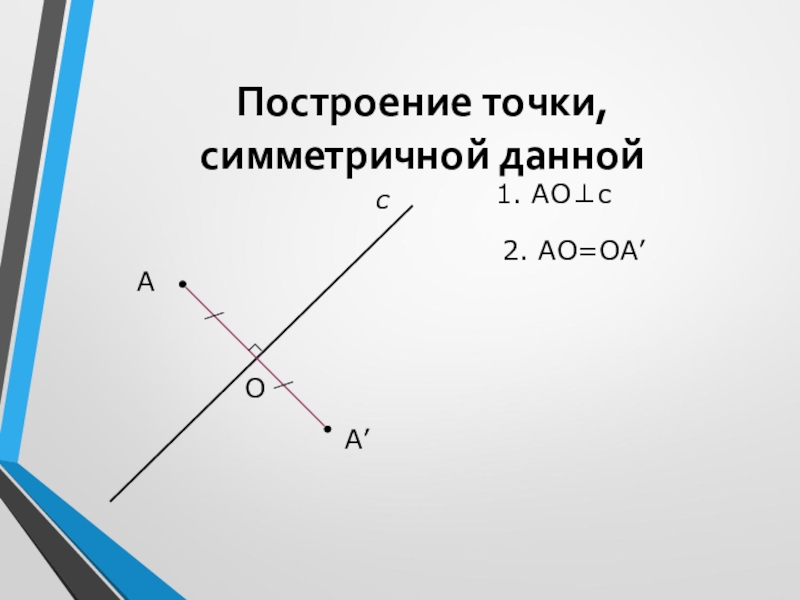
- 11. Построение точки, симметричной даннойАсА’1. АО⊥сО2. АО=ОА’
- 12. Построение отрезка, симметричного данномуАсА’ВВ’OO'АА’⊥с, АО=ОА’.ВВ’⊥с, ВО’=О’В’.3. А’В’ – искомый отрезок.
- 13. Построение треугольника, симметричного данномуАсА’ВВ’СС’1. AA’⊥c AO=OA’2. BB’⊥c BO’=O’B’3. СС’⊥c СO”=O”С’4. ΔA’B’С’ – искомый треугольник.OO”O’
- 14. Для каждого из случаев, представленных на
- 15. Для каждого из случаев, представленных на рисунке,
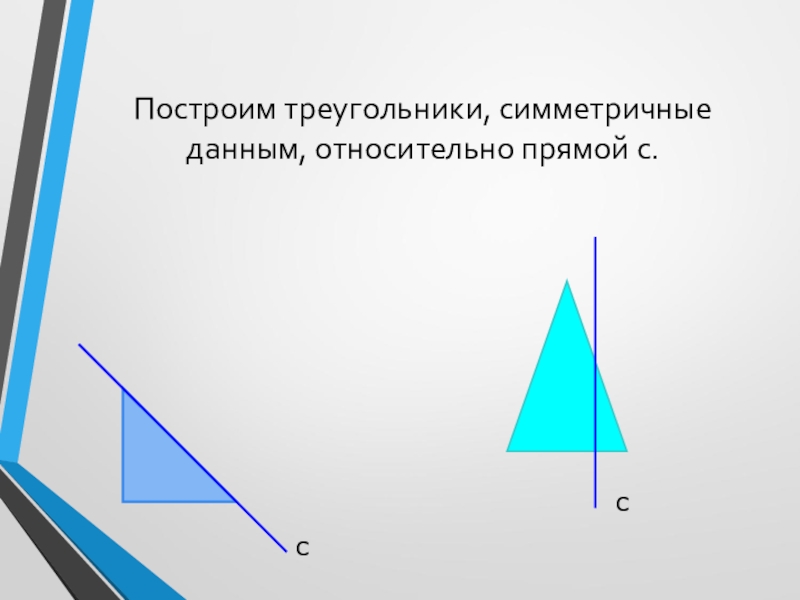
- 16. Построим треугольники, симметричные данным, относительно прямой с.сс
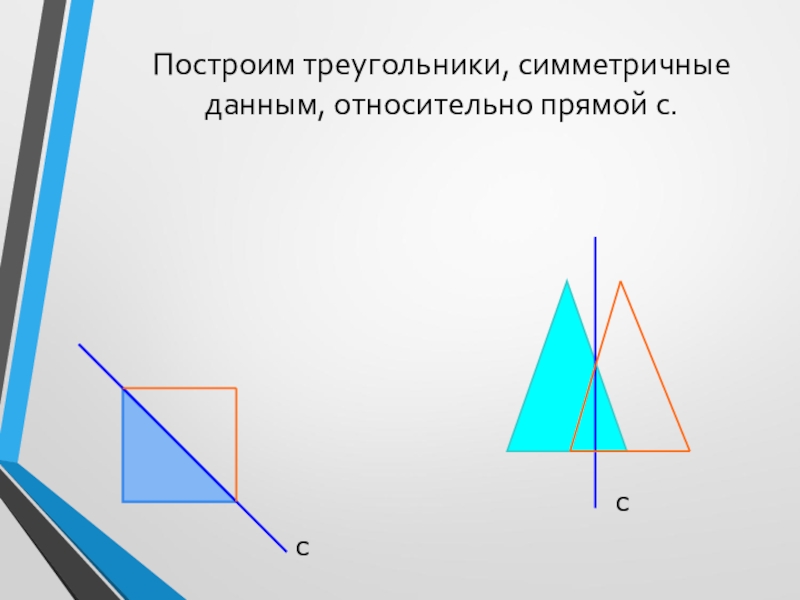
- 17. Построим треугольники, симметричные данным, относительно прямой с.сс
- 18. «Симметрия является той идеей, посредством которой
- 19. Симметрия в природе
- 20. В архитектуре
- 21. Симметрия в искусстве
- 22. Симметрия в поэзии Пушкин А.С. «Медный всадник»
- 23. ЗаключениеСимметрию можно обнаружить почти везде, если знать,
- 24. О симметрия! Гимн тебе пою! Тебя повсюду
Содержание Симметрия Осевая симметрияСимметрия в геометрии, природе, архитектуре, поэзииЗаключение
Слайд 2Содержание
Симметрия
Осевая симметрия
Симметрия в геометрии, природе, архитектуре, поэзии
Заключение
Слайд 3Определение
Симметрия (от греч. Symmetria – соразмерность), в широком смысле – неизменность
структуры материального объекта относительно его преобразований. Симметрия играет огромную роль в искусстве и архитектуре. Но ее можно заметить и в музыке, и в поэзии. Симметрия широко встречается в природе, в особенности у кристаллов, у растений и животных. Симметрия может встретиться и в других разделах математики, например при построении графиков функций.
Слайд 4Осевая симметрия
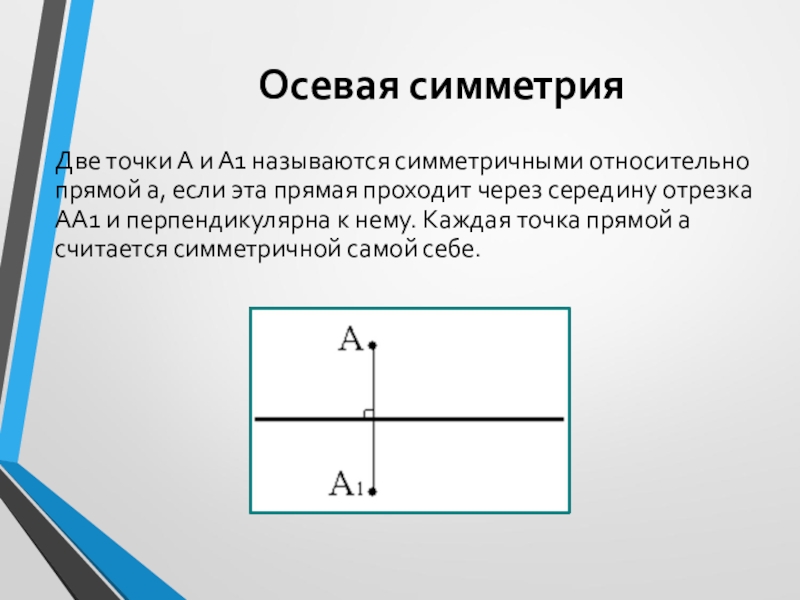
Две точки А и А1 называются симметричными относительно прямой а,
если эта прямая проходит через середину отрезка АА1 и перпендикулярна к нему. Каждая точка прямой а считается симметричной самой себе.
Слайд 5Фигура называется симметричной относительно прямой a, если для каждой точки фигуры
симметричная ей точка относительно прямой а также принадлежит этой фигуре.
Прямая а называется осью симметрии фигуры.
Говорят также, что фигура обладает осевой симметрией.
Прямая а называется осью симметрии фигуры.
Говорят также, что фигура обладает осевой симметрией.
а
Слайд 9Фигуры, не обладающие осевой симметрией
Произвольный треугольник
Параллелограмм
Неправильный многоугольник
Слайд 10Построение
точки, симметричной данной
отрезка, симметричного данному
треугольника, симметричного данному
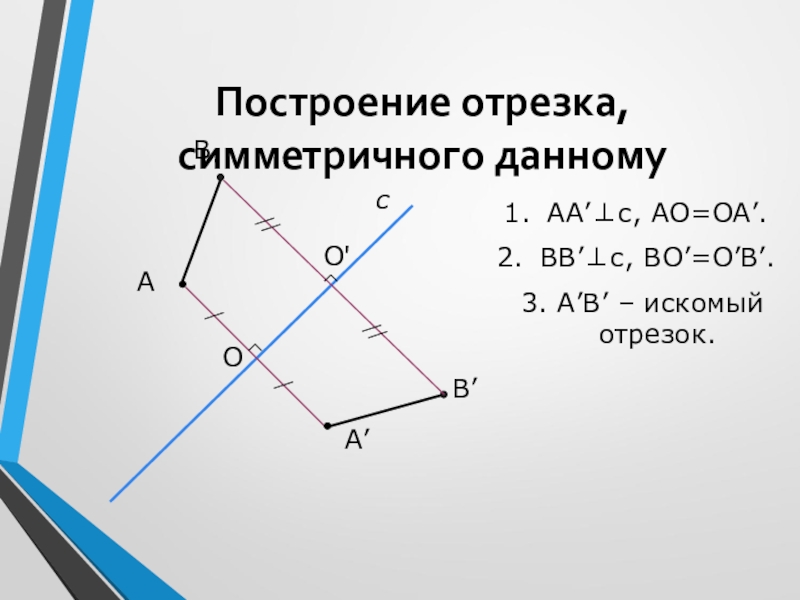
Слайд 12Построение отрезка, симметричного данному
А
с
А’
В
В’
O
O'
АА’⊥с, АО=ОА’.
ВВ’⊥с, ВО’=О’В’.
3. А’В’ – искомый отрезок.
Слайд 13Построение треугольника, симметричного данному
А
с
А’
В
В’
С
С’
1. AA’⊥c AO=OA’
2. BB’⊥c BO’=O’B’
3. СС’⊥c СO”=O”С’
4.
ΔA’B’С’ – искомый треугольник.
O
O”
O’
Слайд 14 Для каждого из случаев, представленных на рисунке, построим точки А'
и В', симметричные точкам А и В, относительно прямой с.
В
А
с
А
В
с
А
В
с
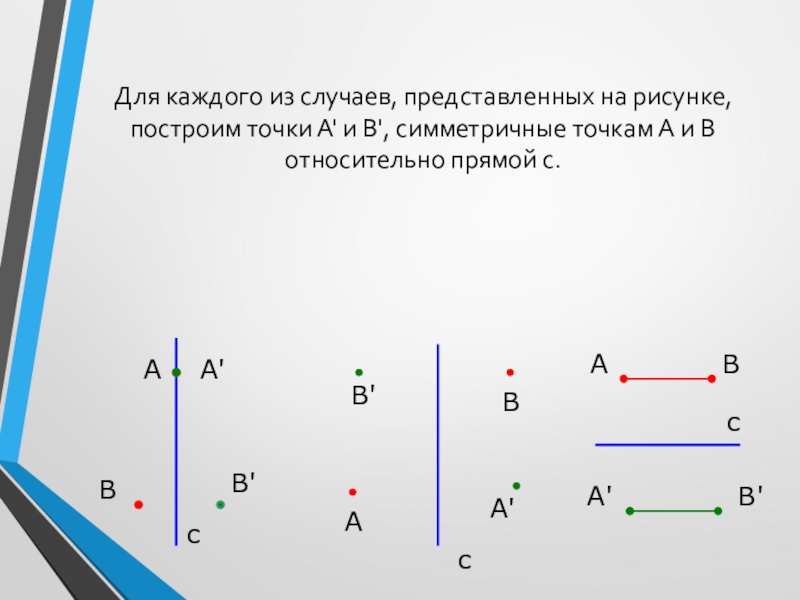
Слайд 15Для каждого из случаев, представленных на рисунке, построим точки А' и
В', симметричные точкам А и В относительно прямой с.
В
В'
А
А'
с
А
А'
В
В'
с
А
В
с
А'
В'
Слайд 18 «Симметрия является той идеей, посредством которой человек на протяжении веков
пытался постичь и создать порядок, красоту и совершенство.»
Г. Вейль
Г. Вейль
Слайд 22Симметрия в поэзии
Пушкин А.С. «Медный всадник»
…В гранит оделася Нева;
Мосты повисли
над водами;
Темнозелеными садами
Ее покрылись острова…
Темнозелеными садами
Ее покрылись острова…
Слайд 23Заключение
Симметрию можно обнаружить почти везде, если знать, как ее искать. Многие
народы с древнейших времен владели представлением о симметрии в широком смысле – как об уравновешенности и гармонии. Творчество людей во всех своих проявлениях тяготеет к симметрии. Посредством симметрии человек всегда пытался, по словам немецкого математика Германа Вейля, «постичь и создать порядок, красоту и совершенство».
Слайд 24О симметрия! Гимн тебе пою! Тебя повсюду в мире узнаю. Ты в Эйфелевой
башне, в малой мошке,
Ты в елочке, что у лесной дорожки!
С тобою в дружбе и тюльпан, и роза,
И снежный рой - творение мороза