- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по теме Объем шара Чувашевой Т.
Содержание
- 1. Презентация по теме Объем шара Чувашевой Т.
- 2. СОДЕРЖАНИЕ.1)Объем шара.2)Объем шарового сегмента.3)Объем шарового слоя.4)Объем шарового сектора.5)Решение задачи.6)Решение «жизненных» задач.7) «Шар вокруг нас».8)Используемая литература..
- 3. ОПРЕДЕЛЕНИЕ ШАРА. Шар - тело, ограниченное сферой..
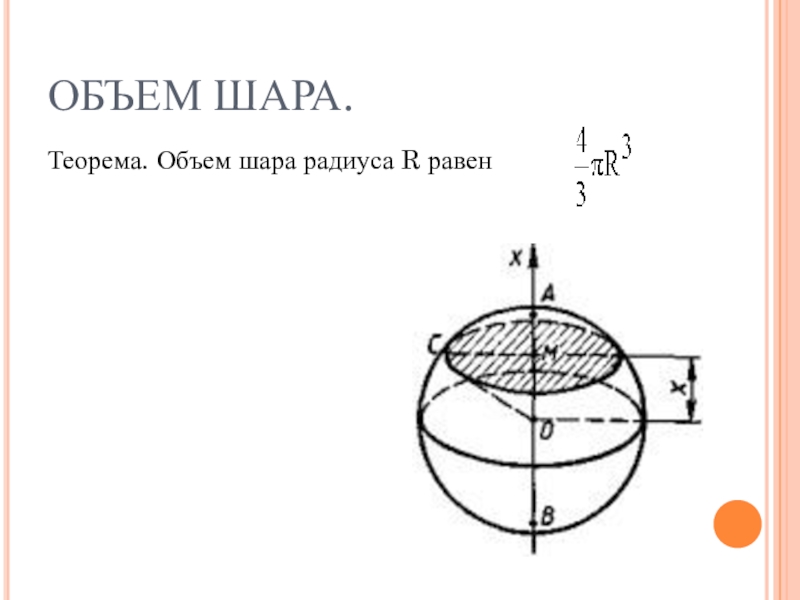
- 4. ОБЪЕМ ШАРА.Теорема. Объем шара радиуса R равен
- 5. ДОКАЗАТЕЛЬСТВО.Рассмотрим шар радиуса R с центром в
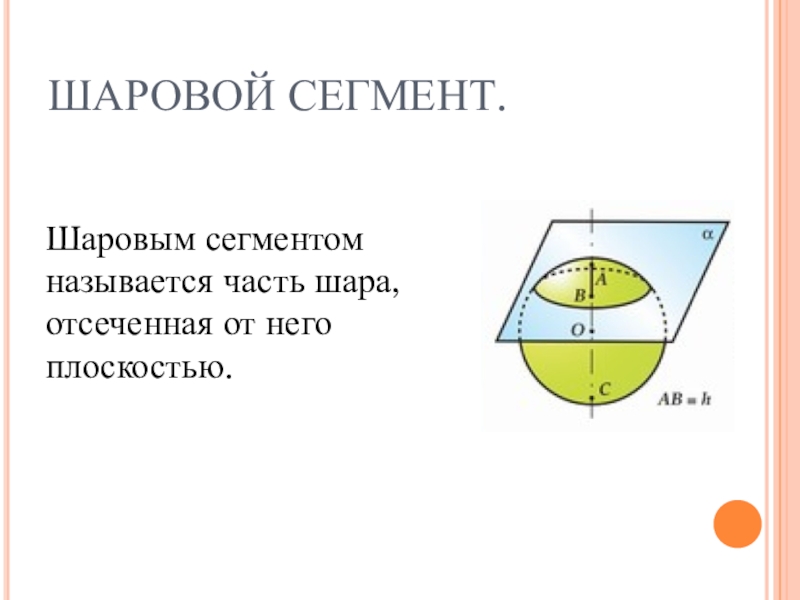
- 6. ШАРОВОЙ СЕГМЕНТ.Шаровым сегментом называется часть шара, отсеченная от него плоскостью.
- 7. ОБЪЕМ ШАРОВОГО СЕГМЕНТА.
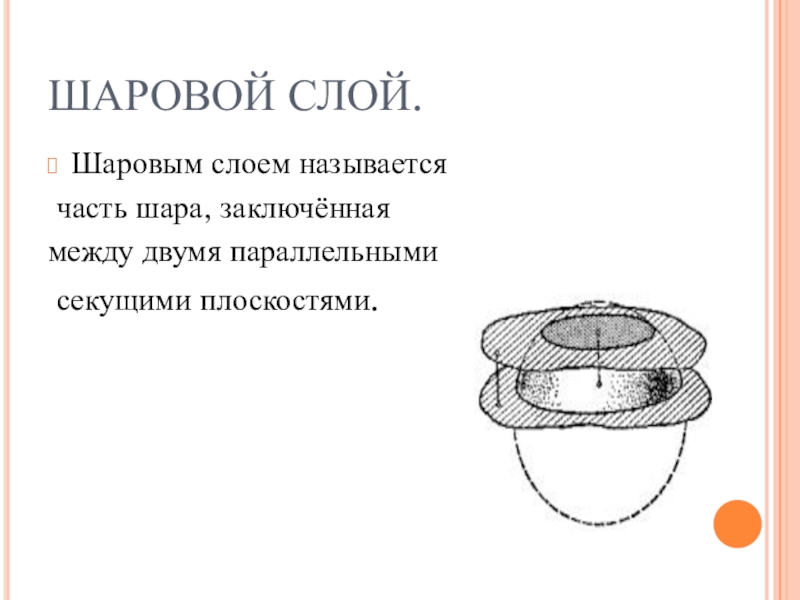
- 8. ШАРОВОЙ СЛОЙ.Шаровым слоем называется часть шара, заключённая между двумя параллельными секущими плоскостями.
- 9. ОБЪЕМ ШАРОВОГО СЛОЯ.Объём шарового слоя можно найти
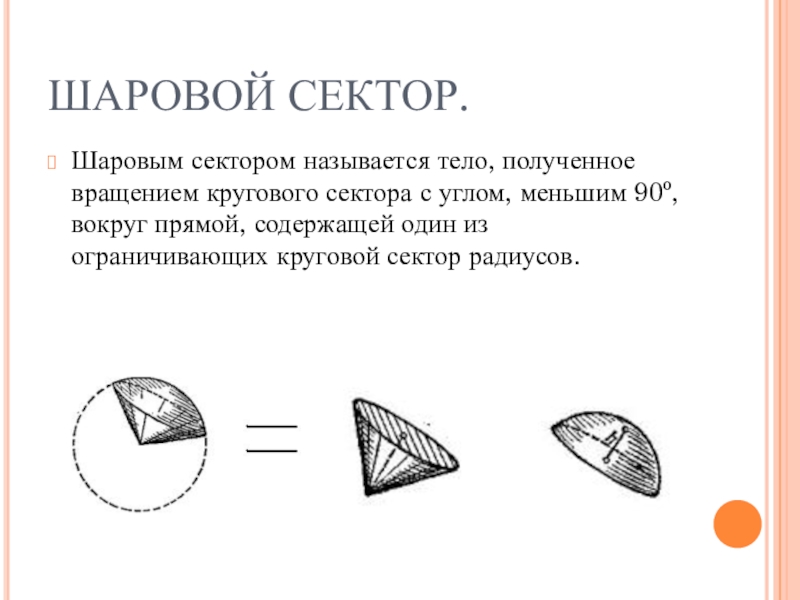
- 10. ШАРОВОЙ СЕКТОР.Шаровым сектором называется тело, полученное вращением
- 11. ОБЪЕМ ШАРОВОГО СЕКТОРА.
- 12. РЕШЕНИЕ ЗАДАЧИ.Задача №1. Найти объём сегмента, отсекаемого
- 13. РЕШЕНИЕ.Диагональ куба, вписанного в шар, является диаметром
- 14. РЕШЕНИЕ «ЖИЗНЕННЫХ» ЗАДАЧ.Чего больше на диске, изображенном на картинке — записанной информации или свободного места?
- 15. РЕШЕНИЕ.С точки зрения математики, и CD– и
- 16. ОТЧЕГО ЖЕ ВОЗНИКАЕТ ТАКОЙ ЭФФЕКТ? Для того,
- 17. НА ПЛОСКОСТИ ШАРОМ ЯВЛЯЕТСЯ КРУГ И, СООТВЕТСТВЕННО,
- 18. Чего больше по объёму в этом апельсине — кожуры или мякоти?
- 19. РЕШЕНИЕ.Кожура занимает, казалось бы, не очень толстый
- 20. «ШАР ВОКРУГ НАС».
- 21. СТЕКЛЯННОЕ ЗДАНИЕ-ШАР В ДРЕЗДЕНЕ
- 22. СВЕТОДИОДНЫЙ СВЕТИЛЬНИК В ФОРМЕ ШАРА LED BALL (OUTDOOR)
- 23. ФЕЙЕРВЕРКИ
- 24. КОМПЛЕКС АДМИНИСТРАТИВНЫХ ЗДАНИЙ ПРАВИТЕЛЬСТВА МОСКВЫ И МОСКОВСКОЙ ГОРОДСКОЙ ДУМЫ.
- 25. ДОМ-ГЛОБУС В ДРЕЗДЕНЕ (1928 Г.)
- 26. Слайд 26
- 27. Слайд 27
- 28. Слайд 28
- 29. Слайд 29
- 30. ИСПОЛЬЗУЕМАЯ ЛИТЕРАТУРА.1)Геометрия (учебник для 10-11 кл.) Л.С.Атанасян.
- 31. СПАСИБО ЗА ВНИМАНИЕ!!!
СОДЕРЖАНИЕ.1)Объем шара.2)Объем шарового сегмента.3)Объем шарового слоя.4)Объем шарового сектора.5)Решение задачи.6)Решение «жизненных» задач.7) «Шар вокруг нас».8)Используемая литература..
Слайд 2СОДЕРЖАНИЕ.
1)Объем шара.
2)Объем шарового сегмента.
3)Объем шарового слоя.
4)Объем шарового сектора.
5)Решение задачи.
6)Решение «жизненных» задач.
7)
«Шар вокруг нас».
8)Используемая литература.
8)Используемая литература.
.
Слайд 5ДОКАЗАТЕЛЬСТВО.
Рассмотрим шар радиуса R с центром в точке О и выберем
ось Ох произвольным образом. Сечение шара плоскостью, перпендикулярной к оси Ох и проходящей через точку М этой оси, является кругом с центром в точке М. Обозначим радиус этого круга через r, а его площадь через S(х), где х — абсцисса точки М. Выразим S(х) через х и R. Из прямоугольного треугольника ОМС находим:
Так как , то
Заметим, что эта формула верна для любого положения точки М на диаметре АВ, т. е. Для всех х, удовлетворяющих условию . Применяя основную формулу для вычисления объемов тел при , ,получим
Теорема доказана.
Так как , то
Заметим, что эта формула верна для любого положения точки М на диаметре АВ, т. е. Для всех х, удовлетворяющих условию . Применяя основную формулу для вычисления объемов тел при , ,получим
Теорема доказана.
Слайд 8ШАРОВОЙ СЛОЙ.
Шаровым слоем называется
часть шара, заключённая
между двумя параллельными
секущими
плоскостями.
Слайд 9ОБЪЕМ ШАРОВОГО СЛОЯ.
Объём шарового слоя можно найти как разность объёмов двух
шаровых сегментов, и запоминать отдельную формулу для его вычисления нет надобности.
Слайд 10ШАРОВОЙ СЕКТОР.
Шаровым сектором называется тело, полученное вращением кругового сектора с углом,
меньшим 90º, вокруг прямой, содержащей один из ограничивающих круговой сектор радиусов.
Слайд 12РЕШЕНИЕ ЗАДАЧИ.
Задача №1. Найти объём сегмента, отсекаемого от шара радиуса R
гранью вписанного в шар куба (при её продолжении).
Слайд 13РЕШЕНИЕ.
Диагональ куба, вписанного в шар, является диаметром шара. Отсюда имеем для
ребра куба
Стрелка сегмента, объём которого мы должны определить, равна
и по формуле для объёма сегмента находим
Ответ: Vсегм= .
Стрелка сегмента, объём которого мы должны определить, равна
и по формуле для объёма сегмента находим
Ответ: Vсегм= .
Слайд 14РЕШЕНИЕ «ЖИЗНЕННЫХ» ЗАДАЧ.
Чего больше на диске, изображенном на картинке — записанной
информации или свободного места?
Слайд 15РЕШЕНИЕ.
С точки зрения математики, и CD– и DVD–диск это кольцо. Радиус
внутренней окружности, ограничивающей круг, на который ничего не пишется, равен двум сантиметрам, а радиус всего стандартного диска — шести сантиметрам. Информация записывается по спиральной дорожке, разматывающейся от меньшей окружности к большей. Так как одинаковому количеству информации соответствует одинаковая длина дорожки, то объем информации, записанной на «болванку», пропорционален площади занятого кольца.
Слайд 16ОТЧЕГО ЖЕ ВОЗНИКАЕТ ТАКОЙ ЭФФЕКТ?
Для того, чтобы была занята ровно половина «болванки»,
внутреннее кольцо должно иметь ширину приблизительно равную 2,5 см, а внешнее кольцо — около 1,5 см.
Слайд 17НА ПЛОСКОСТИ ШАРОМ ЯВЛЯЕТСЯ КРУГ И, СООТВЕТСТВЕННО, ОБЪЁМ ЕСТЬ ПЛОЩАДЬ ЭТОГО
КРУГА. КАК ВЫ ВСЕ ХОРОШО ЗНАЕТЕ, ПЛОЩАДЬ КРУГА РАДИУСА R РАВНА Π•R². ЧТОБЫ ПОСЧИТАТЬ ПЛОЩАДЬ КОЛЬЦА НУЖНО ИЗ ПЛОЩАДИ БОЛЬШОГО КРУГА ВЫЧЕСТЬ ПЛОЩАДЬ НЕИСПОЛЬЗУЕМОГО МАЛЕНЬКОГО — Π•(R²-R²). И ТАК КАК ВСЕ ЗАВИСИТ ОТ РАДИУСА, ДА ЕЩЕ В КВАДРАТЕ, ТО, ЧЕМ БЛИЖЕ К БОЛЬШЕМУ РАДИУСУ ОПИСАНО КОЛЬЦО, ТЕМ БОЛЬШЕ, ПРИ ТОЙ ЖЕ ШИРИНЕ, ЕГО ВКЛАД В ПЛОЩАДЬ.
В нашем трехмерном пространстве объём шара зависит от радиуса, возведенного в третью степень. А значит, и рассматриваемый эффект становится еще более выраженным: большая часть объёма шара сосредоточена рядом с границей!
Слайд 19РЕШЕНИЕ.
Кожура занимает, казалось бы, не очень толстый слой, но он расположен
рядом с границей шара. И его объём на приведенном рисунке равен объёму всей вкусной части апельсина. Покупая апельсин с толстой кожурой, по объёму Вы приобретаете в основном кожуру.(!!!)
Слайд 30ИСПОЛЬЗУЕМАЯ ЛИТЕРАТУРА.
1)Геометрия (учебник для 10-11 кл.) Л.С.Атанасян. М. «Просвещение» 1994 г.
2)»Математика
в формулах и таблицах» 5-11 кл. Справочное пособие. Дрофа 2002 г.
3) «Энциклопедический словарь юного математика». М. «Педагогика» 1989 г.
4)Ресурсы интернета.
3) «Энциклопедический словарь юного математика». М. «Педагогика» 1989 г.
4)Ресурсы интернета.