- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по теме Н.И. Лобаческий
Содержание
- 1. Презентация по теме Н.И. Лобаческий
- 2. ЛобачевскийН.И. Лобачевский родился в Нижнем Новгороде в
- 3. Будучи студентом, он пользовался особенным расположением профессора Бартельса, который заметил в нем необыкновенные дарование к математике.Лобачевский
- 4. В 1811 году он был утвержден магистром
- 5. В 1811 году он был утвержден магистром
- 6. В 1816 году он занял кафедру чистой
- 7. Он присутствовал на всех заседаниях, которых
- 8. Все его сочинения были направлены
- 9. Случайно на важность системы Лобачевского указали
- 10. Труды Лобачевского
- 11. Через данную точку вне данной прямой
- 12. Предложение 10.Параллельные прямые сближаются неопределенно по направлению
- 13. Если какую-нибудь поверхность будем изгибать
- 14. Постоянная кривизна поверхности может быть
- 15. Плоскости Лобачевского
- 16. К сожалению Лобачевский умер непризнанным.Но сейчас
- 17. В честь Лобачевского назван кратер на
ЛобачевскийН.И. Лобачевский родился в Нижнем Новгороде в 1793 году.Воспитывался в Казанской гимназии В 1807 году поступил в Казанский университет в числе студентов математического факультета
Слайд 2Лобачевский
Н.И. Лобачевский родился в Нижнем Новгороде в 1793 году.
Воспитывался в Казанской
гимназии
В 1807 году поступил в Казанский университет в числе студентов математического факультета
В 1807 году поступил в Казанский университет в числе студентов математического факультета
Слайд 3
Будучи студентом, он пользовался особенным расположением профессора Бартельса, который заметил в
нем необыкновенные дарование к математике.
Лобачевский
Слайд 4
В 1811 году он был утвержден магистром математических наук и начал
свою преподавательскую деятельность в Университете изложением Небесной Механики Лапласа и Disquisitiones arifmeticae Гаусса.
Лобачевский
Слайд 5
В 1811 году он был утвержден магистром математических наук и начал
свою преподавательскую деятельность в Университете изложением Небесной Механики Лапласа и Disquisitiones arifmeticae Гаусса.
Лобачевский
Слайд 6
В 1816 году он занял кафедру чистой математики и с этого
времени начинаются ученые труды Лобачевского.
Он был 6 раз сряду избираем ректором университета, пробыл в этой должности 19 лет
Он был 6 раз сряду избираем ректором университета, пробыл в этой должности 19 лет
Лобачевский
Слайд 7 Он присутствовал на всех заседаниях, которых было в то время
очень много.
Читал лекции за всех профессоров, посылаемых за границу.
Присутствовал на всех экзаменах и был не строг, но иногда своенравен, требовал ответов не бойких, но показывающих развитие.
Читал лекции за всех профессоров, посылаемых за границу.
Присутствовал на всех экзаменах и был не строг, но иногда своенравен, требовал ответов не бойких, но показывающих развитие.
Лобачевский
Слайд 8 Все его сочинения были направлены на то, чтобы восполнить
пробел в Евклидовой геометрической системе.
Для восполнения этого пробела он предпринял построение системы, независимой от одиннадцатой аксиомы.
Сорок лет его сочинения были в забвении…
Для восполнения этого пробела он предпринял построение системы, независимой от одиннадцатой аксиомы.
Сорок лет его сочинения были в забвении…
Труды Лобачевского
Слайд 9 Случайно на важность системы Лобачевского указали Гаусс, а потом Риман,
Бельтрами, Гельмгольц.
Тогда его сочинения были переведены на немецкий, французский, и итальянский языки.
Имя Лобачевского сделалось европейским.
Тогда его сочинения были переведены на немецкий, французский, и итальянский языки.
Имя Лобачевского сделалось европейским.
Труды Лобачевского
Слайд 11 Через данную точку вне данной прямой можно провести по крайней
мере одну прямую, не встречающую данную.
Если эта прямая
-единственная, то мы
имеем плоскую геометрию, геометрию Евклида.
Если мы можем провести несколько таких прямых, то получим систему Лобачевского или Неевклидову геометрию.
Если эта прямая
-единственная, то мы
имеем плоскую геометрию, геометрию Евклида.
Если мы можем провести несколько таких прямых, то получим систему Лобачевского или Неевклидову геометрию.
Система Лобачевского
Слайд 12Предложение 10.
Параллельные прямые сближаются неопределенно по направлению их параллельности.
Предложение 11.
Геометрическое место
равно отстоящих точек от данной прямой есть кривая линия.
Система Лобачевского
Слайд 13 Если какую-нибудь поверхность будем изгибать всеми возможными способами, но
такими, при которых не образовались бы ни складки ни разрывы, то получим все поверхности, которые могут быть навиты одна на другую. Так как при выгибании поверхности, кривизна её в каждой точке не изменяется, следовательно , чтобы одна поверхность была навита на другую, необходимо, чтобы в соответствующих точках, кривизны поверхностей были равны.
Кривизна
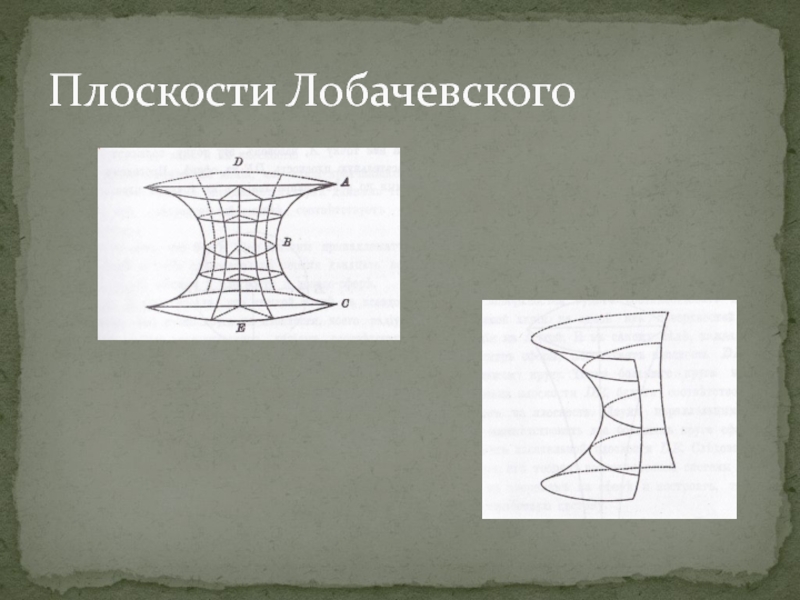
Слайд 14 Постоянная кривизна поверхности может быть нуль, положительная и отрицательная.
Тип поверхностей с кривизной раной нулю служит плоскость.
Тип поверхностей с положительной кривизной служит сфера.
Тип поверхностей с отрицательной кривизной служит псевдо-сфера или плоскость Лобачевского.
Тип поверхностей с положительной кривизной служит сфера.
Тип поверхностей с отрицательной кривизной служит псевдо-сфера или плоскость Лобачевского.
Кривизна
Слайд 16 К сожалению Лобачевский умер непризнанным.
Но сейчас правда восторжествовала.
Лобачевский признан в
всем мире и является гордостью России.
Его имя стоит наравне с Евклидом и другими великими математиками.
Его имя стоит наравне с Евклидом и другими великими математиками.
Лобачевский
Слайд 17
В честь Лобачевского назван кратер на Луне.
Его имя носят также
улицы в Москве и Казани, научная библиотека Казанского университета.
Лобачевский
