- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по теме Методы решения геометрических задач по математике (10 - 11 классы)
Содержание
- 1. Презентация по теме Методы решения геометрических задач по математике (10 - 11 классы)
- 2. Трудности решения геометрических задач обусловлены как объективными,
- 3. Необходимые условия успеха при решении
- 4. Метод дополнительных построенийРазновидности:Продолжение отрезка (отрезков) на определенное
- 5. Задача 1В основании четырехугольной пирамиды SABCD лежит
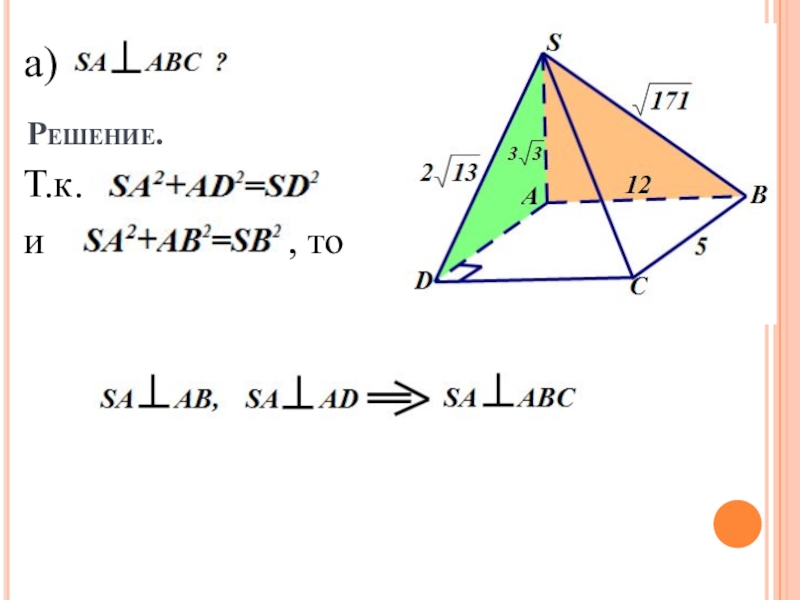
- 6. Решение.а)Т.к. и, то
- 7. На прямой AD отложим отрезок DE=AD. Тогда
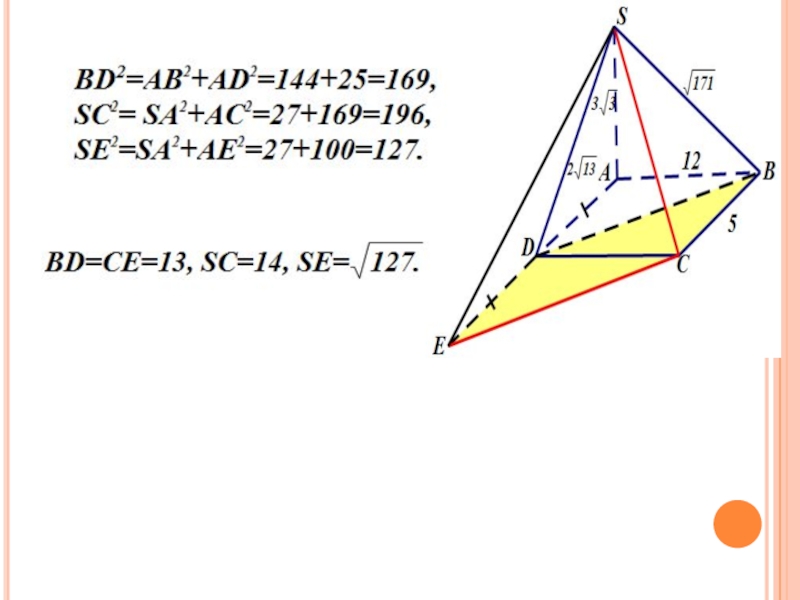
- 8. Слайд 8
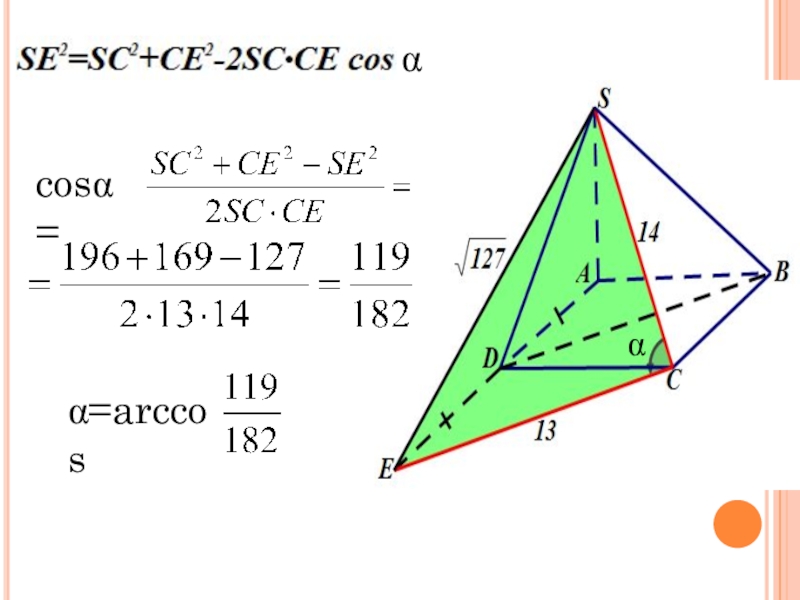
- 9. ααcosα=α=arccos
- 10. Метод подобия
- 11. Задача 2На ребрах AA1, СС1, С1D1 прямоугольного
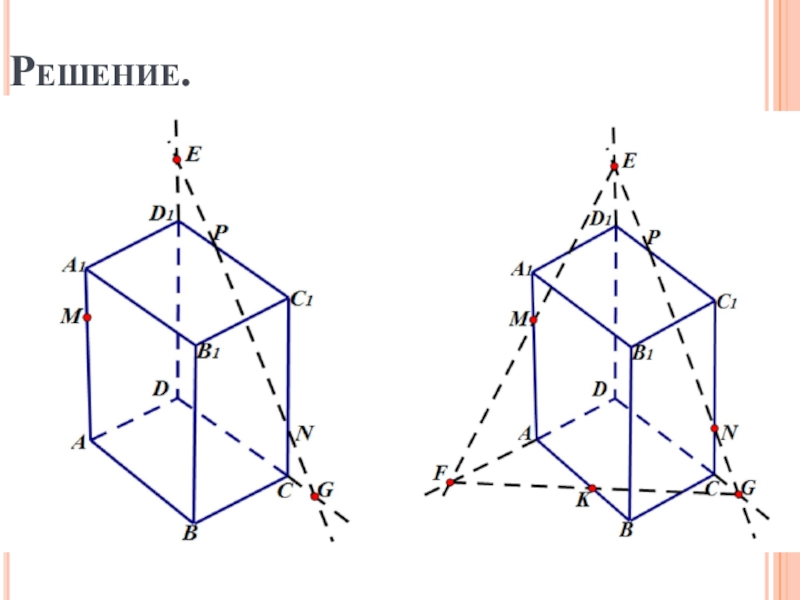
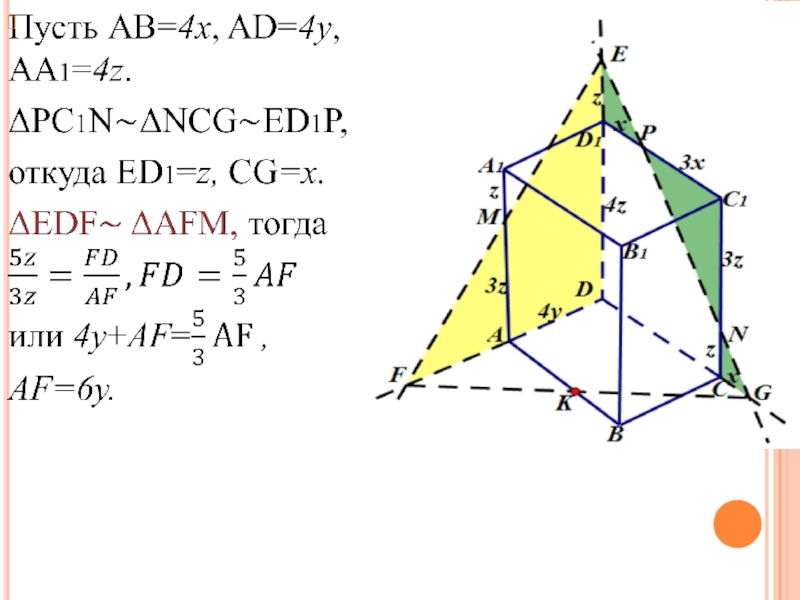
- 12. Решение.
- 13. Слайд 13
- 14. Слайд 14
- 15. Метод координатМетод координат и векторный метод -
- 16. Расстояние от точки до плоскостиввести удобную для
- 17. Задача 3В правильной треугольной пирамиде SABC высота
- 18. Решение.Построить плоскость α :PTα,α ||SH.а) В плоскостях
- 19. б) α=PTT0.Из ∆ SHB1 по теореме Пифагора
- 20. Расстояние от точки M(x0,y0) до прямой, заданной
- 21. Угол между прямымиввести удобную для данной фигуры
- 22. Угол между прямой и плоскостьюввести удобную для
- 23. Угол между плоскостямиввести удобную для данной фигуры
- 24. «Лучше решить задачу десятью способами, чем десять задач одним».
Слайд 2Трудности решения геометрических задач обусловлены как объективными, так и субъективными факторами,
Неалгоритмичность задач
Необходимость выбора метода решения задачи и теоремы для решения конкретной задачи (нескольких теорем) из большого набора известных фактов
Нужно решить довольно много задач (чтобы научиться их решать) за небольшое время
Слайд 3Необходимые условия успеха
при решении задач по геометрии
Уверенное владение основными
Знание основных методов и приемов решения задач;
Умение комбинировать методы и приемы решения задач;
Наличие опыта решения задач.
Слайд 4Метод дополнительных построений
Разновидности:
Продолжение отрезка (отрезков) на определенное расстояние или до пересечения
Проведение прямой через две заданные точки.
Проведение через заданную точку прямой, параллельной данной прямой, или перпендикулярной данной прямой.
Слайд 5Задача 1
В основании четырехугольной пирамиды SABCD лежит прямоугольник со сторонами AB=12,
а) Докажите, что SA – высота пирамиды;
б) Найдите угол между SC и BD.
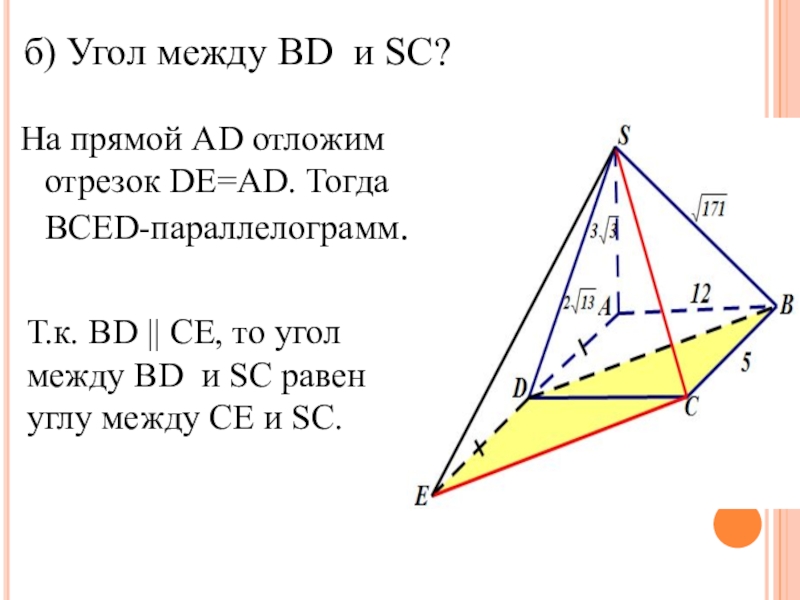
Слайд 7На прямой AD отложим отрезок DE=AD. Тогда BCED-параллелограмм.
б) Угол между BD
Т.к. BD || CE, то угол между BD и SC равен углу между СE и SC.
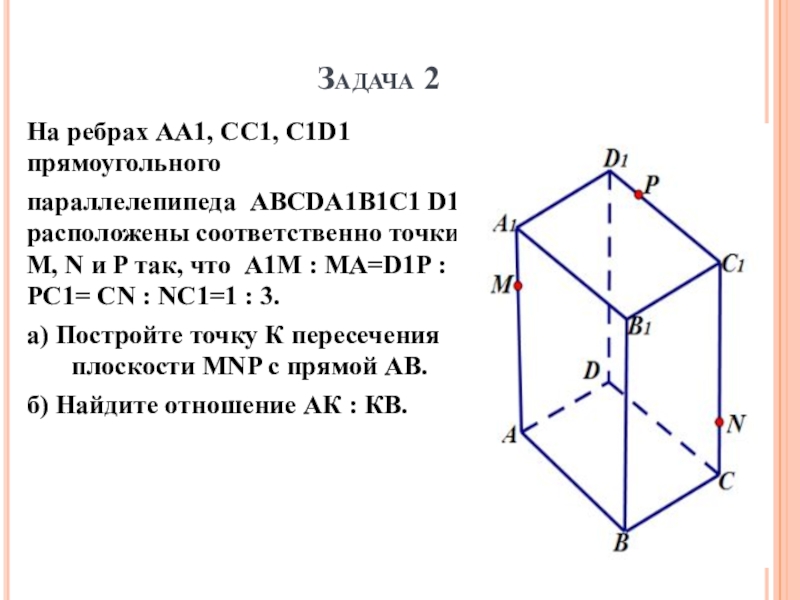
Слайд 11Задача 2
На ребрах AA1, СС1, С1D1 прямоугольного
параллелепипеда ABCDA1B1С1 D1 расположены
а) Постройте точку К пересечения плоскости MNP с прямой АВ.
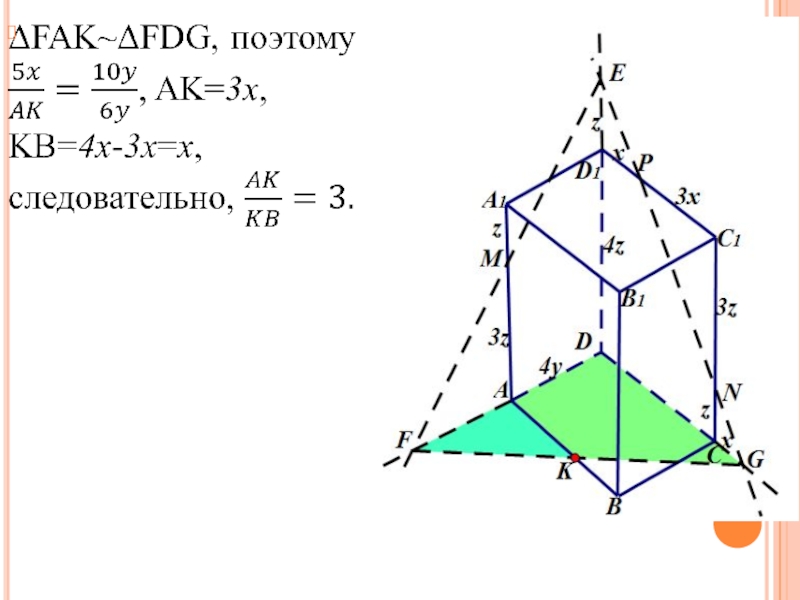
б) Найдите отношение АК : КВ.
Слайд 15Метод координат
Метод координат и векторный метод - самые универсальные методы геометрии.
Главное - удачно выбрать систему координат.
I тип – задачи на нахождение зависимости между элементами данной фигуры;
II тип – задачи на составление уравнения данной фигуры, если известны характеристические свойства точек данной фигуры.
Слайд 16Расстояние от точки до плоскости
ввести удобную для данной фигуры прямоугольную систему
задать координаты трех точек плоскости и точки, от которой необходимо найти расстояние
составить уравнение плоскости
по формуле расстояния вычислить его
Слайд 17Задача 3
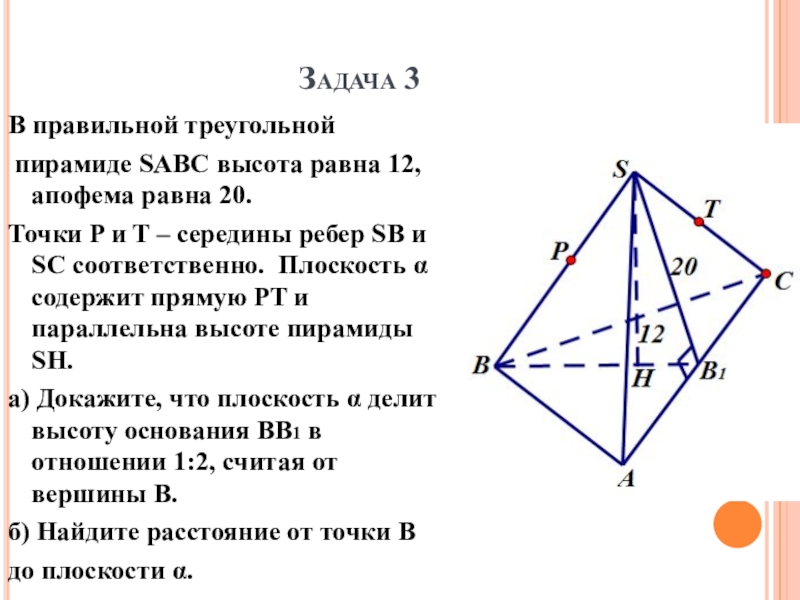
В правильной треугольной
пирамиде SABC высота равна 12, апофема равна
Точки P и T – середины ребер SB и SC соответственно. Плоскость α содержит прямую PT и параллельна высоте пирамиды SH.
а) Докажите, что плоскость α делит высоту основания BB1 в отношении 1:2, считая от вершины В.
б) Найдите расстояние от точки В
до плоскости α.
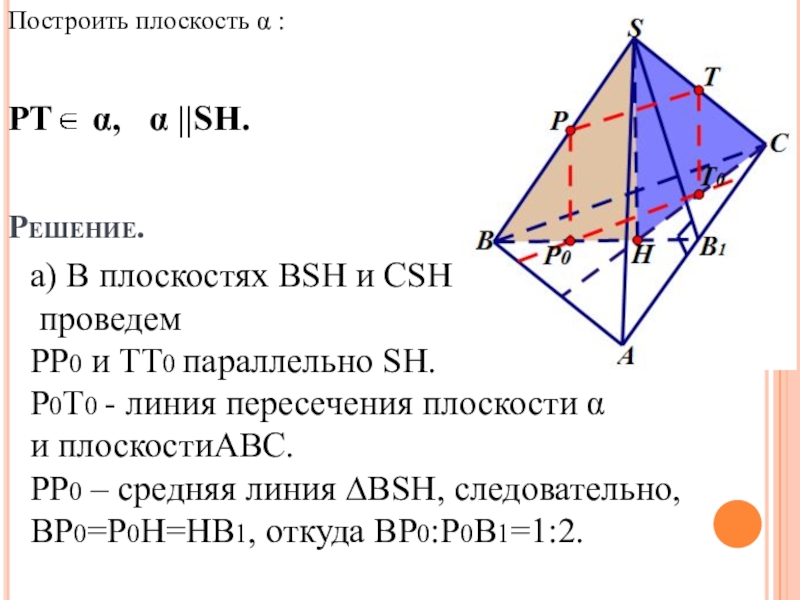
Слайд 18Решение.
Построить плоскость α :
PT
α,
α ||SH.
а) В плоскостях BSH и CSH
проведем
PP0 и TT0 параллельно SH.
P0T0 - линия пересечения плоскости α
и плоскостиABC.
PP0 – средняя линия ∆BSH, следовательно,
BP0=P0H=HB1, откуда BP0:P0B1=1:2.
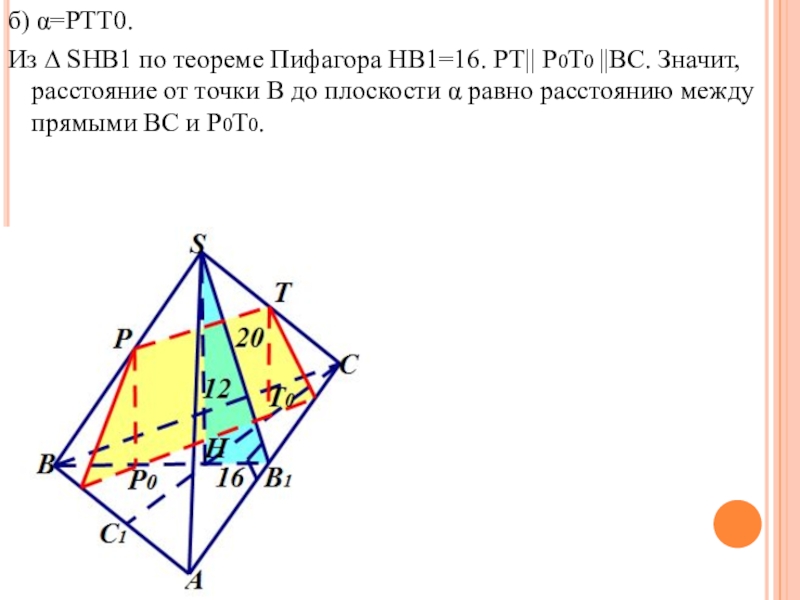
Слайд 19б) α=PTT0.
Из ∆ SHB1 по теореме Пифагора HB1=16. PT|| P0T0 ||BC.
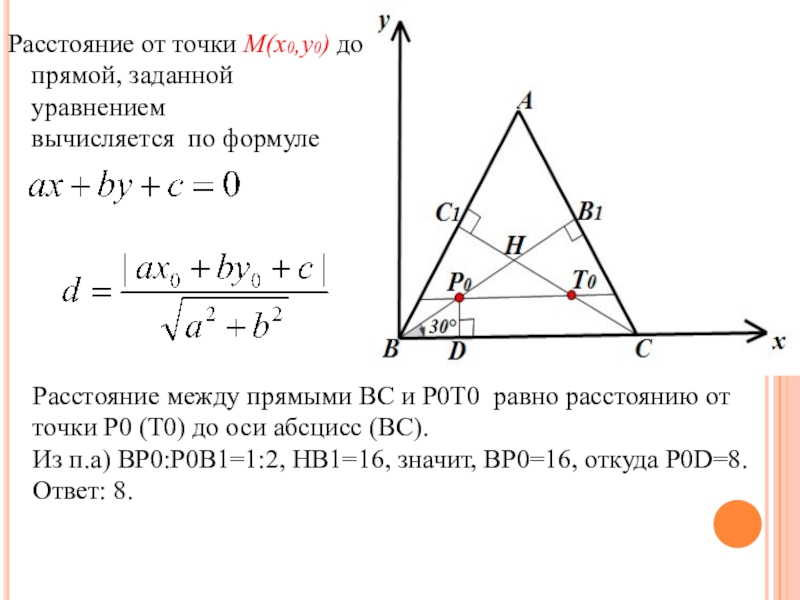
Слайд 20Расстояние от точки M(x0,y0) до прямой, заданной уравнением
Расстояние между прямыми BC и P0T0 равно расстоянию от точки P0 (T0) до оси абсцисс (ВС).
Из п.а) BP0:P0B1=1:2, HB1=16, значит, BP0=16, откуда P0D=8.
Ответ: 8.
Слайд 21Угол между прямыми
ввести удобную для данной фигуры прямоугольную систему координат
определить направляющие
вычислить координаты направляющих векторов
по формуле вычисления косинуса угла между векторами определить искомый угол
Слайд 22Угол между прямой и плоскостью
ввести удобную для данной фигуры прямоугольную систему
определить нормаль плоскости (вектор, перпендикулярный к плоскости) и вычислить его координаты
вычислить координаты направляющего вектора прямой
по формуле вычисления косинуса угла между векторами определить искомый угол, так как синус угла между прямой и плоскостью будет равен косинусу угла между нормалью и направляющим вектором прямой.
Слайд 23Угол между плоскостями
ввести удобную для данной фигуры прямоугольную систему координат
определить нормали
по формуле вычисления косинуса угла между векторами определить искомый угол. Косинус угла между плоскостями равен модулю косинуса угла между их нормальными векторами.