- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по теме Конус. Площадь поверхности конуса
Содержание
- 1. Презентация по теме Конус. Площадь поверхности конуса
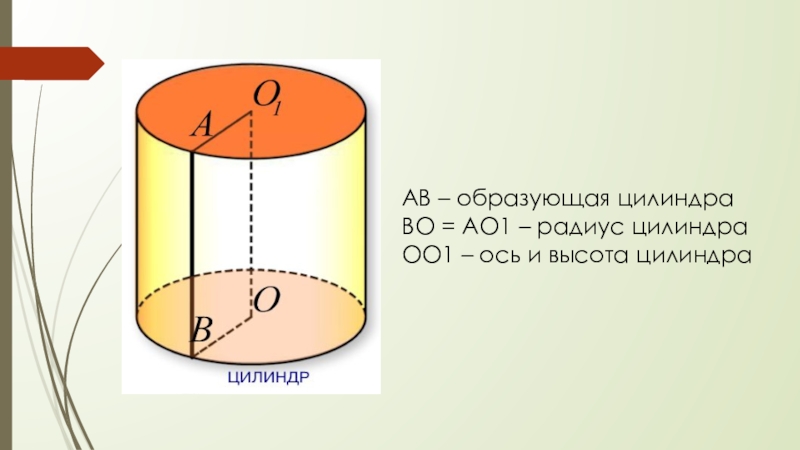
- 2. АВ – образующая цилиндраВО = АО1 – радиус цилиндраОО1 – ось и высота цилиндра
- 3. Вопрос №1: Какая фигура является основанием цилиндра?а) Овалб) Кругв) Квадрат
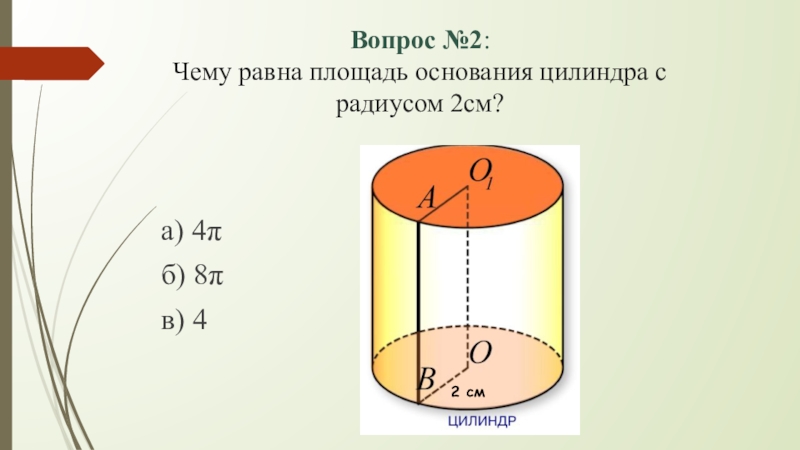
- 4. Вопрос №2: Чему равна площадь основания цилиндра с радиусом 2см?а) 4πб) 8πв) 42 см
- 5. Вопрос №3: Как называется отрезок АВ?а) диагональ цилиндраб) апофема цилиндрав)образующая цилиндра
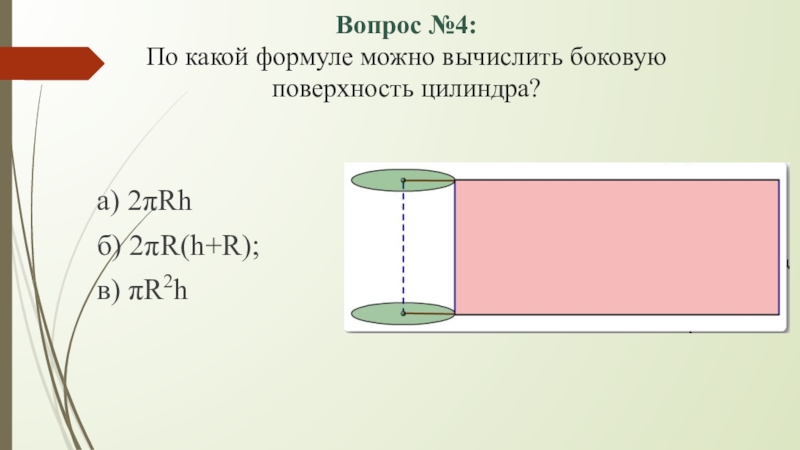
- 6. Вопрос №4: По какой формуле можно вычислить боковую поверхность цилиндра?а) 2πRhб) 2πR(h+R); в) πR2h
- 7. Вопрос №5: По какой формуле можно вычислить полную поверхность цилиндра?а) πR2hб) 2πRh в) 2πR(h+R)
- 8. Вопрос №6: Вычислите боковую поверхность данного цилиндра.а) 15π см2б) 30π см2в) 48π см25 см3 см
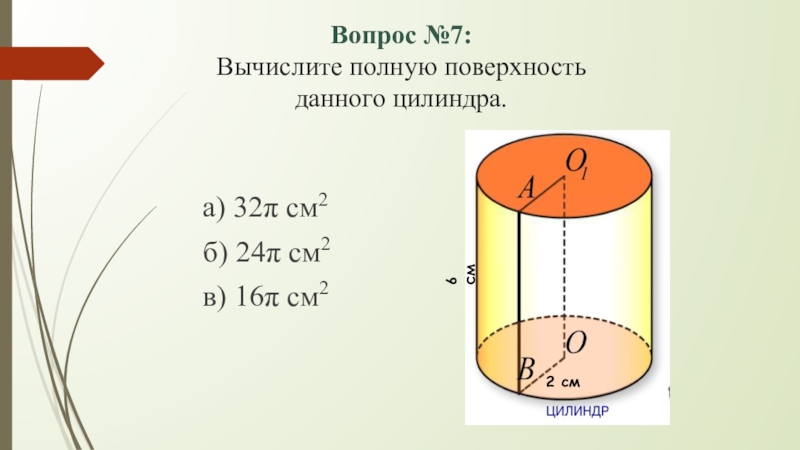
- 9. Вопрос №7: Вычислите полную поверхность данного цилиндра.а) 32π см2б) 24π см2в) 16π см26 см2 см
- 10. Вопрос №8: Чему равна площадь осевого сечения
- 11. Правильные ответы:На оценку «5»-8 правильных ответов.На оценку
- 12. Конус в переводе с греческого «konos» означает
- 13. Архимед(287 до н. э. — 212 до
- 14. Демокрит (470-380 гг. до н.э.)Демокрит получил формулу для вычисления объема пирамиды и конуса.
- 15. Платон (428-348 гг. до н.э.). Школе Платона
- 16. Аполлоний Пергский(260-170 гг. до н.э.) Написал большой трактат о конических сечениях
- 17. Конус выноса (геология)Конус выноса — Это форма
- 18. КОНУС НАРАСТАНИЯ (биология) Конус нарастания: 1
- 19. Конусы – ядовитые моллюски?Конусы – это представители
- 20. Название «конусы» эти моллюски получили за идеально
- 21. Построение конуса с помощью образующейКоническая поверхностьКонус -
- 22. Построение конуса с помощью прямоугольного треугольникаКатет ВС
- 23. Сечение конусаОсевое сечениеСечение плоскостью,
- 24. Развертка конуса Sбок= πRLSосн= πR2Sполн= πRL + πR2
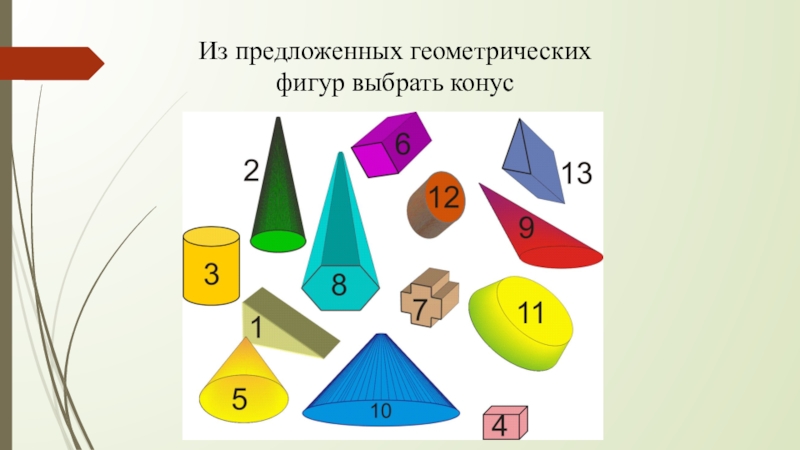
- 25. Из предложенных геометрических фигур выбрать конус
- 26. Оценка 5 – все выполнено верно. Оценка
- 27. Оценка 5 – все выполнено верно. Оценка
АВ – образующая цилиндраВО = АО1 – радиус цилиндраОО1 – ось и высота цилиндра
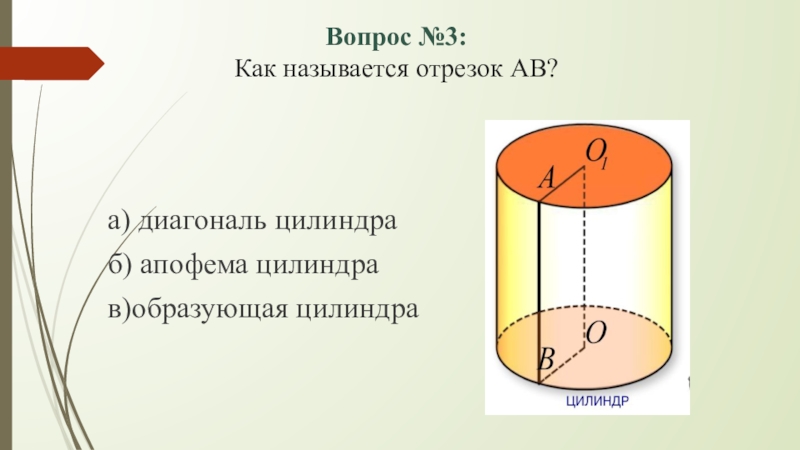
Слайд 5Вопрос №3:
Как называется отрезок АВ?
а) диагональ цилиндра
б) апофема цилиндра
в)образующая цилиндра
Слайд 6Вопрос №4:
По какой формуле можно вычислить боковую поверхность цилиндра?
а) 2πRh
б) 2πR(h+R);
в) πR2h
Слайд 7Вопрос №5:
По какой формуле можно вычислить полную поверхность цилиндра?
а) πR2h
б) 2πRh
в) 2πR(h+R)
Слайд 8Вопрос №6:
Вычислите боковую поверхность
данного цилиндра.
а) 15π см2
б) 30π см2
в) 48π
см2
5 см
3 см
Слайд 9Вопрос №7:
Вычислите полную поверхность
данного цилиндра.
а) 32π см2
б) 24π см2
в) 16π
см2
6 см
2 см
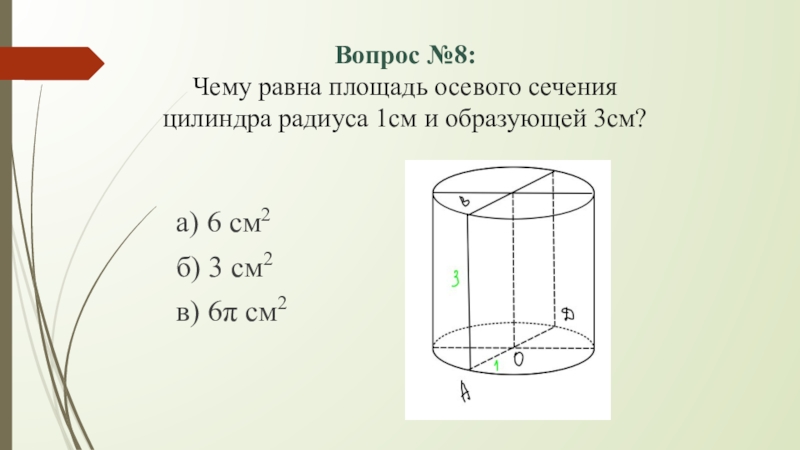
Слайд 10Вопрос №8: Чему равна площадь осевого сечения цилиндра радиуса 1см и образующей
3см?
а) 6 см2
б) 3 см2
в) 6π см2
Слайд 11Правильные ответы:
На оценку «5»-8 правильных ответов.
На оценку «4»- 6-7 правильных ответов.
На
оценку «3»- 5 правильных ответов.
На оценку «2»- 4 и менее правильных ответов.
На оценку «2»- 4 и менее правильных ответов.
Слайд 12Конус в переводе с греческого «konos» означает «кегля», «верхушка шлема»
«сосновая шишка»,
остроконечный предмет.
Этот термин встречается у Евклида и Архимеда.
Этот термин встречается у Евклида и Архимеда.
Историческая справка о конусе
Слайд 13Архимед
(287 до н. э. — 212 до н. э.)
В 1906 году
была обнаружена книга Архимеда (287-212 гг. до н.э.) “О методе”, в которой дается решение задачи об объеме общей части пересекающихся цилиндров.
Слайд 14Демокрит
(470-380 гг. до н.э.)
Демокрит получил формулу для вычисления объема пирамиды
и конуса.
Слайд 15Платон
(428-348 гг. до н.э.).
Школе Платона принадлежит:
а) исследование свойств
призмы, пирамиды, цилиндра и конуса;
б) изучение конических сечений.
б) изучение конических сечений.
Слайд 17Конус выноса (геология)
Конус выноса — Это форма рельефа, образованная скоплением обломочных
пород (гальки, гравия, песка), вынесенными горными реками на предгорную равнину или в более плоскую широкую долину.
Слайд 18КОНУС НАРАСТАНИЯ (биология)
Конус нарастания: 1 — внешний вид верхушки побега
водяной сосенки; 2, 3 — конус нарастания её стебля с поверхности и в разрезе.
Это верхушка побега и корня растений, состоящая из клеток образовательной ткани.
Слайд 19Конусы – ядовитые моллюски?
Конусы – это представители брюхоногих моллюсков, они получили
известность среди ученых не только за свои невообразимые окрасы и формы, но и за свою ядовитость.
Слайд 20Название «конусы» эти моллюски получили за идеально правильную форму своих раковин.
Их «домик», который они всегда носят на себе, имеет вид закрученной спирали.
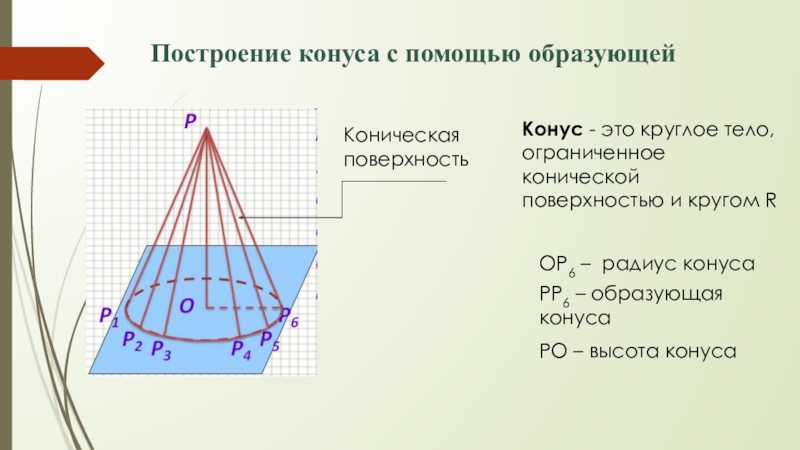
Слайд 21Построение конуса с помощью образующей
Коническая поверхность
Конус - это круглое тело, ограниченное
конической поверхностью и кругом R
ОP6 – радиус конуса
PP6 – образующая конуса
PO – высота конуса
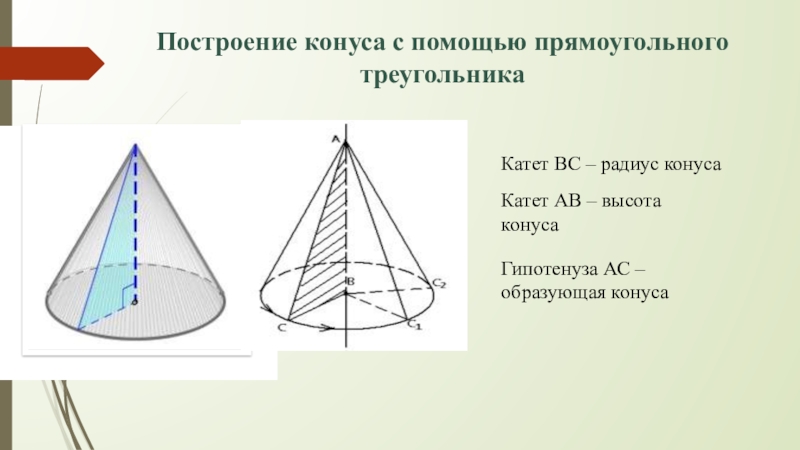
Слайд 22Построение конуса с помощью прямоугольного треугольника
Катет ВС – радиус конуса
Катет АВ
– высота конуса
Гипотенуза АС – образующая конуса
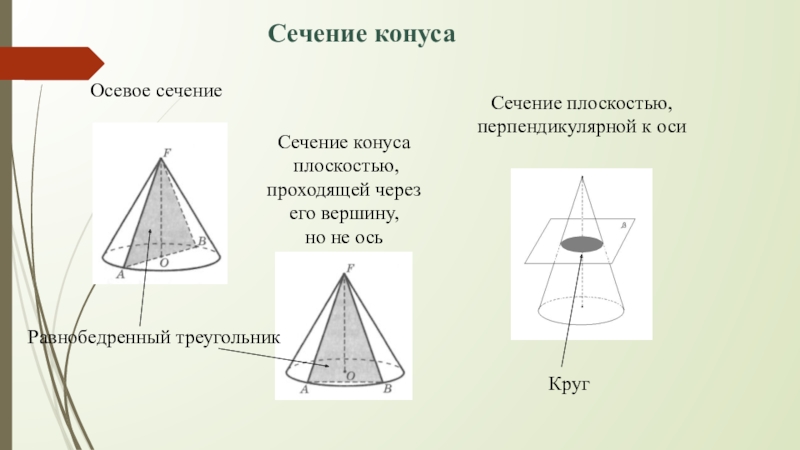
Слайд 23Сечение конуса
Осевое сечение
Сечение плоскостью, перпендикулярной к оси
Сечение конуса
плоскостью,
проходящей через его вершину,
но не ось
Круг
Равнобедренный треугольник
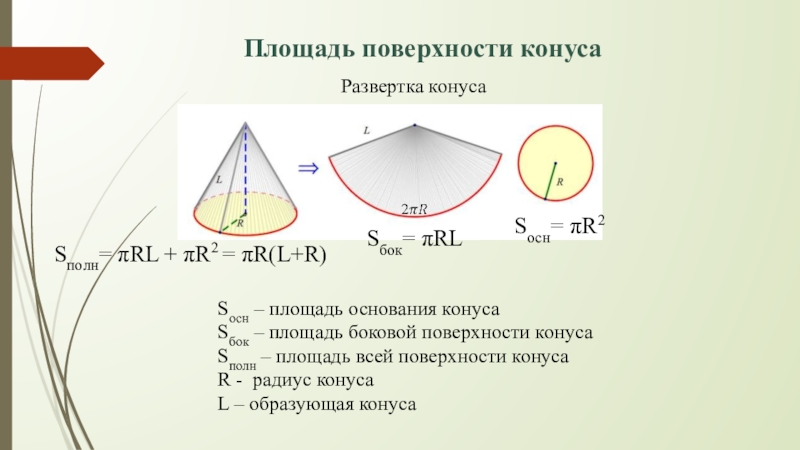
Слайд 24Развертка конуса
Sбок= πRL
Sосн= πR2
Sполн= πRL + πR2 = πR(L+R)
Площадь поверхности конуса
Sосн
– площадь основания конуса
Sбок – площадь боковой поверхности конуса
Sполн – площадь всей поверхности конуса
R - радиус конуса
L – образующая конуса
Sбок – площадь боковой поверхности конуса
Sполн – площадь всей поверхности конуса
R - радиус конуса
L – образующая конуса
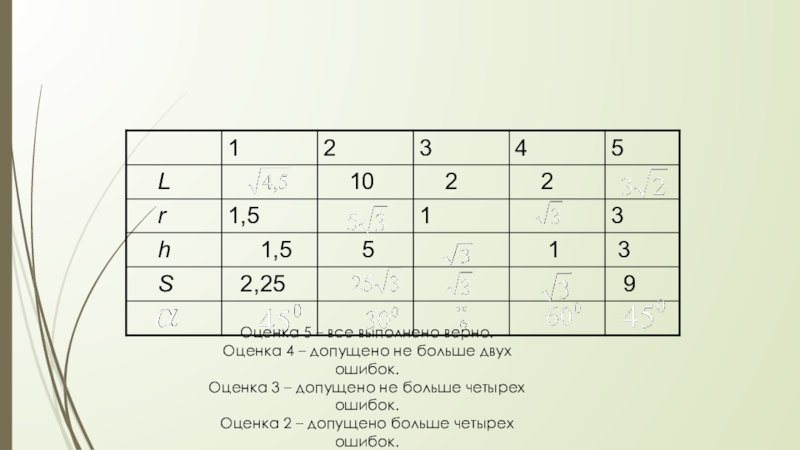
Слайд 26Оценка 5 – все выполнено верно.
Оценка 4 – допущено не
больше двух ошибок.
Оценка 3 – допущено не больше четырех ошибок.
Оценка 2 – допущено больше четырех ошибок.
Оценка 3 – допущено не больше четырех ошибок.
Оценка 2 – допущено больше четырех ошибок.
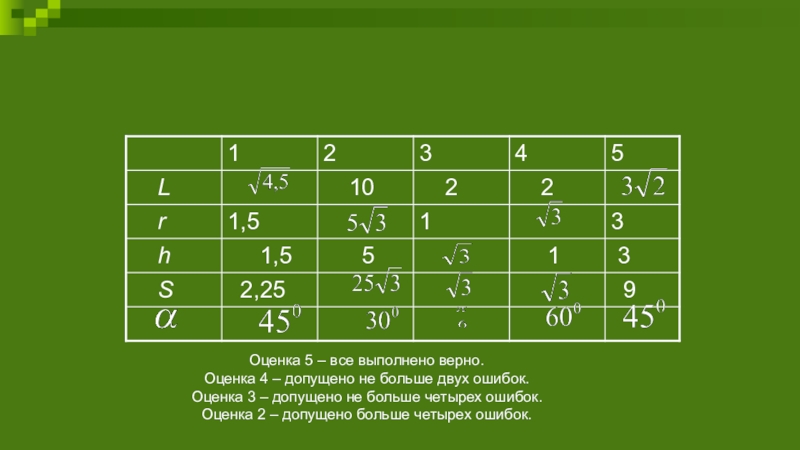
Слайд 27Оценка 5 – все выполнено верно.
Оценка 4 – допущено не
больше двух ошибок.
Оценка 3 – допущено не больше четырех ошибок.
Оценка 2 – допущено больше четырех ошибок.
Оценка 3 – допущено не больше четырех ошибок.
Оценка 2 – допущено больше четырех ошибок.
