Опарина Татьяна Викторовна
МКОУ СОШ п.Комсомольский Котельничского района
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по теме Изучение нового материала по теме Соотношения между сторонами и улами треугольника в 7 классе на основе деятельностного подхода.
Содержание
- 1. Презентация по теме Изучение нового материала по теме Соотношения между сторонами и улами треугольника в 7 классе на основе деятельностного подхода.
- 2. Особенности деятельностного подходаЗнания добываются, создаются учеником в
- 3. Сумма углов треугольника Лабораторная работаЦель:
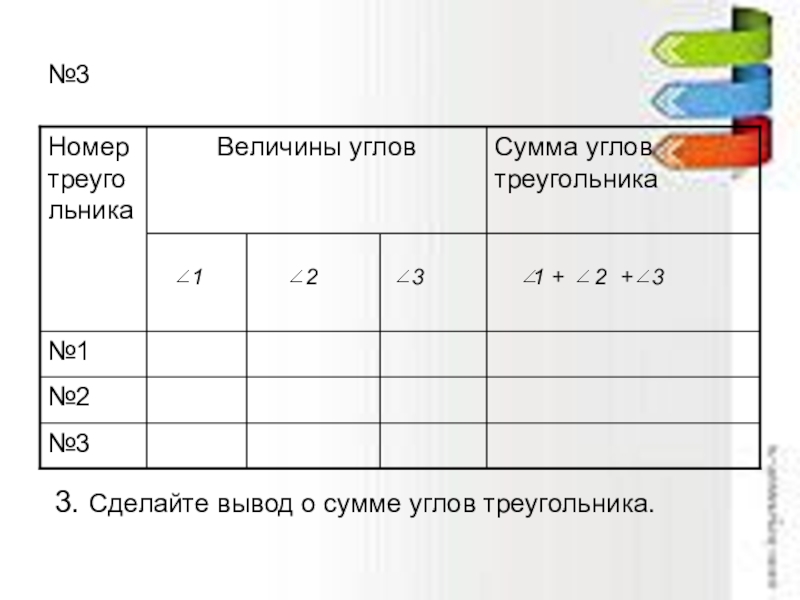
- 4. №33. Сделайте вывод о сумме углов треугольника.
- 5. Практическая работа Перед вами на столе
- 6. Положите желтый треугольник на стол,
- 7. Посмотрите внимательно, что у вас получилось? Какой
- 8. Доказательство теоремы о сумме углов треугольникаЦель: доказать
- 9. Дано: _____ Доказать:
- 10. Внешний угол треугольникаЦель: исследовать свойство внешнего угла
- 11. 65° Заполните таблицу
- 12. Проверка
- 13. Какую закономерность вы заметили? (Сравните внешний угол
- 14. Составление кластераКластер (англ. «сluster» - скопление) –
- 15. Задание: составить кластер по теме «Виды треугольников»Сначала
- 16. Виды треугольниковВиды треугольниковРавностороннийРавнобедренныйРазностороннийОстроугольныйПрямоугольныйТупоугольный
- 17. В ΔАВС известны
- 18. 81°Запишите в таблице буквы, соответствующие найденным ответам,
- 19. Лабораторная работа «Соотношения между сторонами и углами
- 20. N=
- 21. Сделайте вывод о соотношении между наибольшей стороной
- 22. Признак равнобедренного треугольникаЦель: сформулировать признак равнобедренного треугольника.Задание:Начертите равнобедренный ΔАВС.АСВ
- 23. ФормулировкаСформулируйте свойство углов при основании равнобедренного треугольника
- 24. А Учащимся предлагается рисунок и
- 25. Неравенство треугольника Практическая работа
- 26. Сделайте вывод о существовании треугольника.Измерьте длины сторон
- 27. Знает даже младший школьник,Что такое треугольник.Каждый знает
- 28. Некоторые свойства прямоугольных треугольников Лабораторная работаЦель:
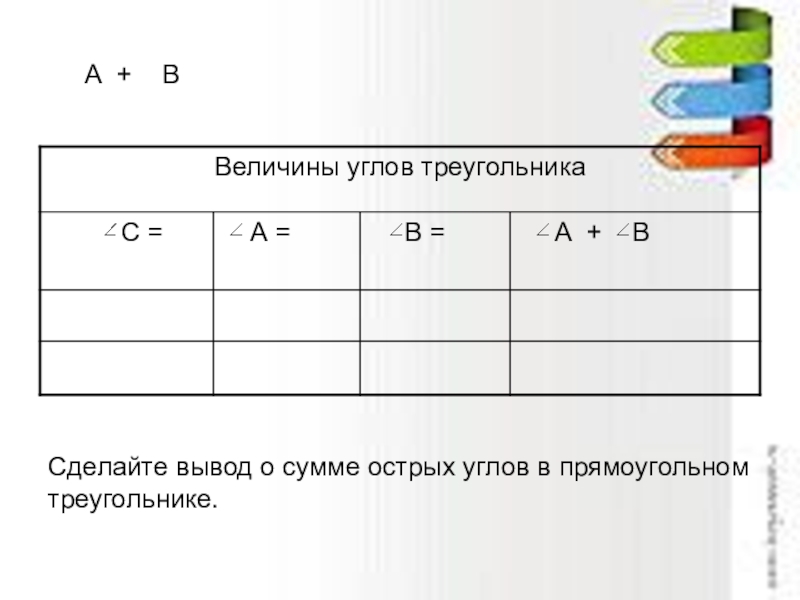
- 29. А + ВСделайте вывод о сумме острых углов в прямоугольном треугольнике.
- 30. Лабораторная работа Цель: определить свойство катета
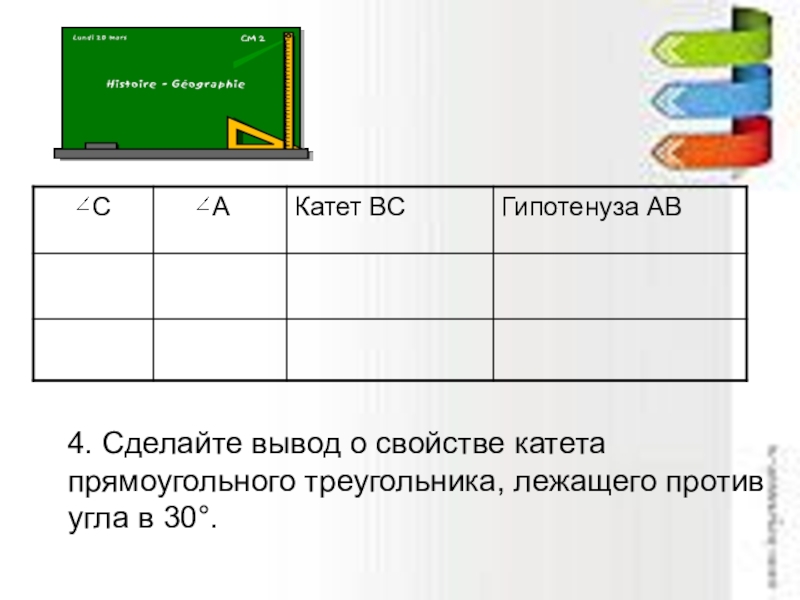
- 31. 4. Сделайте вывод о свойстве катета прямоугольного треугольника, лежащего противугла в 30°.
- 32. Поднимите каждый свой треугольник. Легко заметить, что
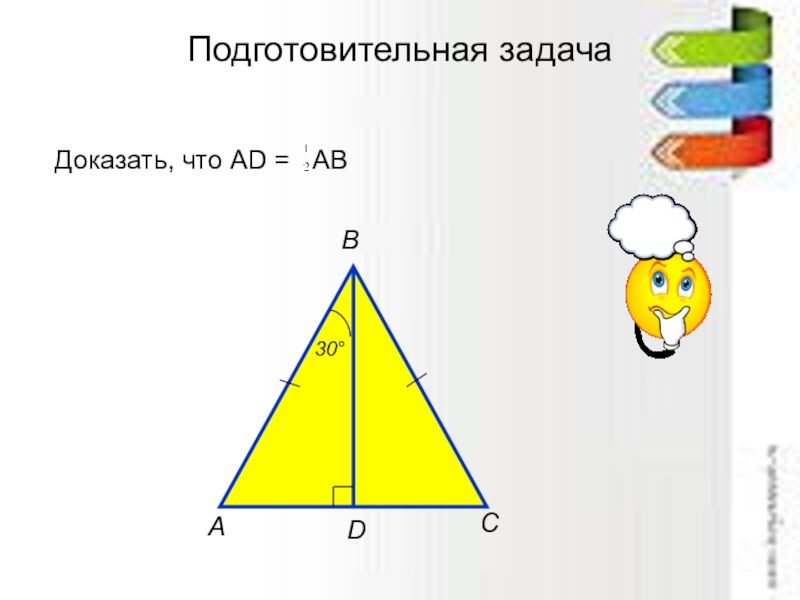
- 33. Подготовительная задача Доказать, что АD = АВ30°АВСD
- 34. Третье свойство прямоугольных треугольников Используя
- 35. 4 Выберите треугольники, которые обладают указанным свойством485105,5111234,28,5147102045630°30°30°30°30°60°
- 36. Признаки равенства прямоугольных треугольников Учащиеся
- 37. Задание:Сформулируй теорему.Выполни рисунок.Запиши, что дано, что
- 38. По готовому чертежу формулируем признак равенства прямоугольных
- 39. Синквейн – стих по математике
- 40. Правила написания «синквейна»Первая строка – слово (существительное,
- 41. Прямоугольный треугольникРавнобедренный, равный.Чертить, доказывать, находить углы.Длина гипотенузы больше катета.Фигура.
- 42. Расстояние от точки до прямой
- 43. Инструкция для учащихся 1. Используя
- 44. АИспользуя рисунок, укажите:Отрезок, который является перпендикуляром, проведённым
- 45. 3. Сделайте записи:АС – перпендикуляр, АВ, АD
- 46. Основные приёмы, использованные при изучении темыЛабораторная работа;Практическая
- 47. Видишь ли у нас тут надобежать изо
Слайд 1Изучение нового материала по теме «Соотношения между сторонами и углами треугольника»
Слайд 2Особенности деятельностного подхода
Знания добываются, создаются учеником в процессе личной работы (под
Учебный процесс выстраивается на систематическом включении разных творческих заданий, необходимых для формирования личности ученика, его качеств и умений;
Учитываются индивидуальные особенности учащихся и их субъектный опыт;
Ведётся обучение умениям работать с алгоритмами.
Слайд 3Сумма углов треугольника
Лабораторная работа
Цель: определить сумму углов треугольника.
Оборудование:
Задание:
Измерьте углы треугольников №1, №2, №3.
Результаты измерений запишите в таблицу.
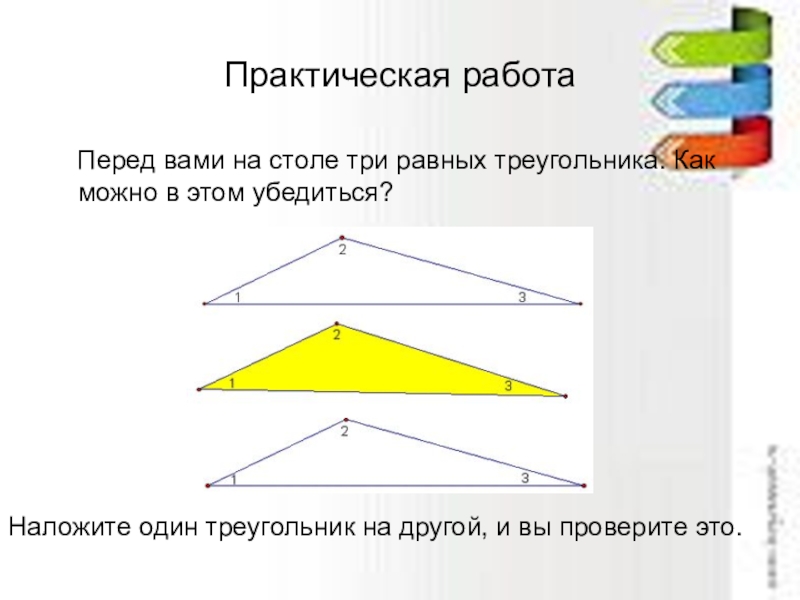
Слайд 5Практическая работа
Перед вами на столе три равных треугольника. Как
Наложите один треугольник на другой, и вы проверите это.
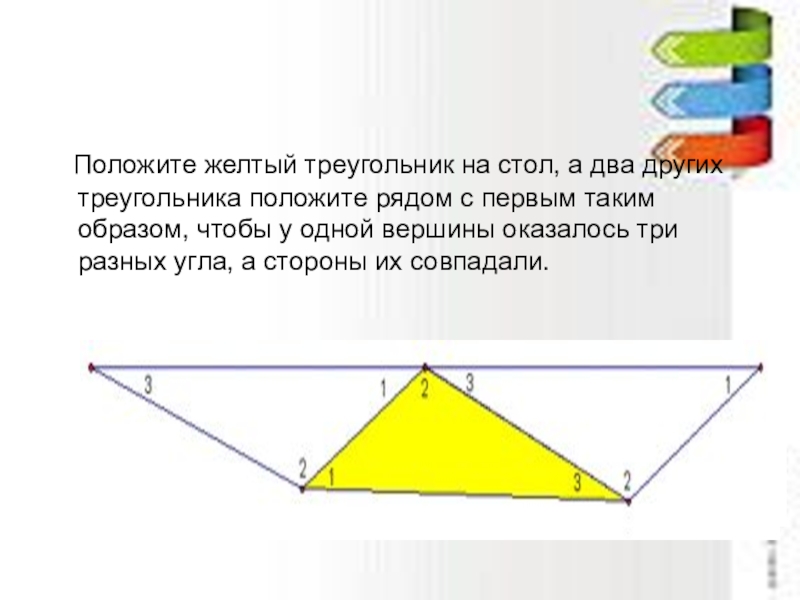
Слайд 6
Положите желтый треугольник на стол, а два других треугольника
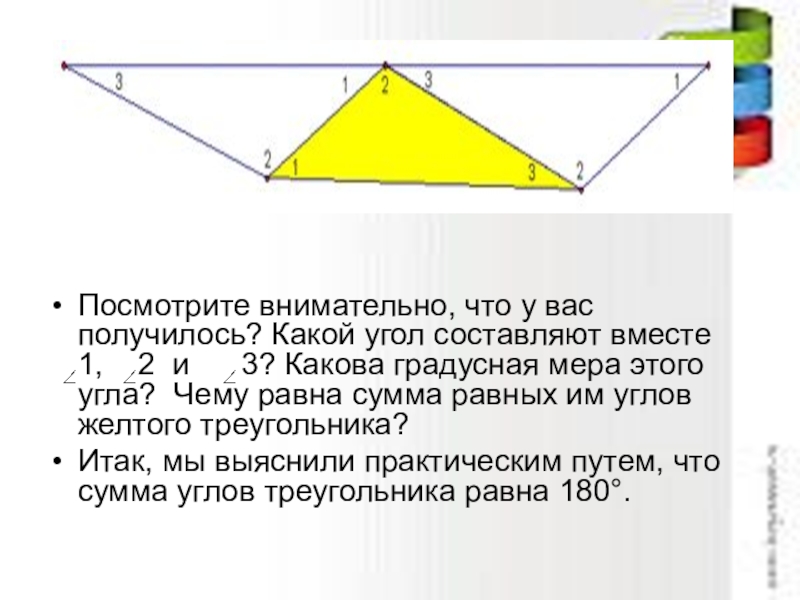
Слайд 7
Посмотрите внимательно, что у вас получилось? Какой угол составляют вместе
Итак, мы выяснили практическим путем, что сумма углов треугольника равна 180°.
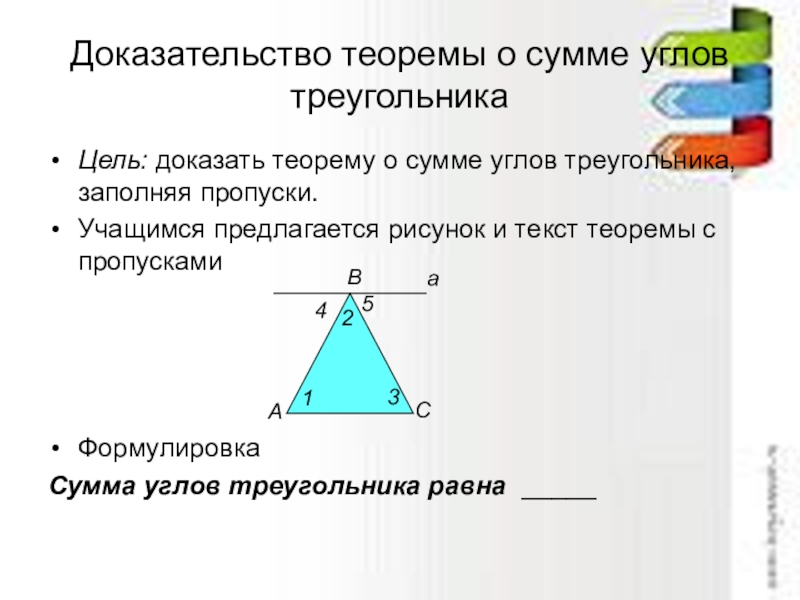
Слайд 8Доказательство теоремы о сумме углов треугольника
Цель: доказать теорему о сумме углов
Учащимся предлагается рисунок и текст теоремы с пропусками
Формулировка
Сумма углов треугольника равна _____
А
В
С
1
2
3
4
5
a
Слайд 9
Дано: _____
Доказать: А + B +
Доказательство:
Проведём через вершину __, прямую а, параллельную прямой ___.
4 = 1, так как это накрест _______ углы при АС II __ и секущей __.
5 = 3, так как это _______ _____ ____
при __ II __ и _______ __.
4 + 2 + 5 = ___, так как они составляют ____________ угол.
Заменим 4 на 1, 5 на __ , получим ______ =180°.
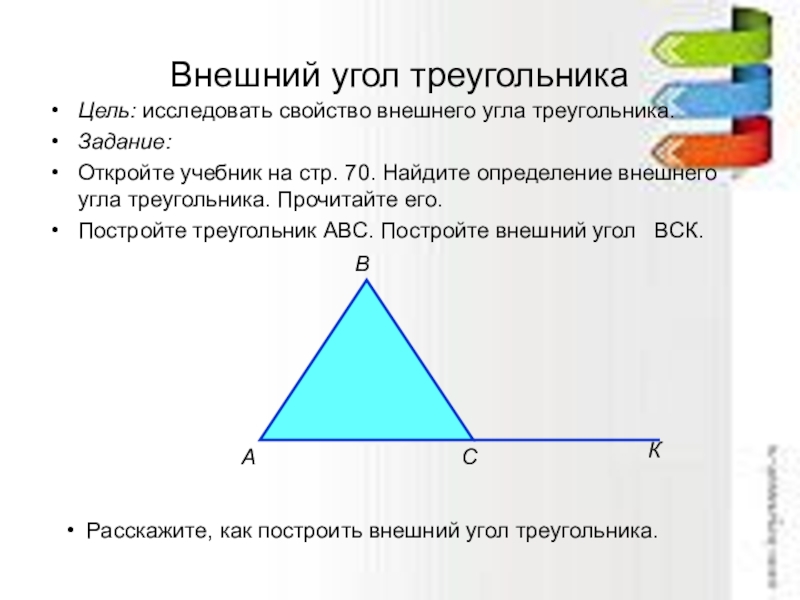
Слайд 10Внешний угол треугольника
Цель: исследовать свойство внешнего угла треугольника.
Задание:
Откройте учебник на
Постройте треугольник АВС. Постройте внешний угол ВСК.
А
В
С
К
Расскажите, как построить внешний угол треугольника.
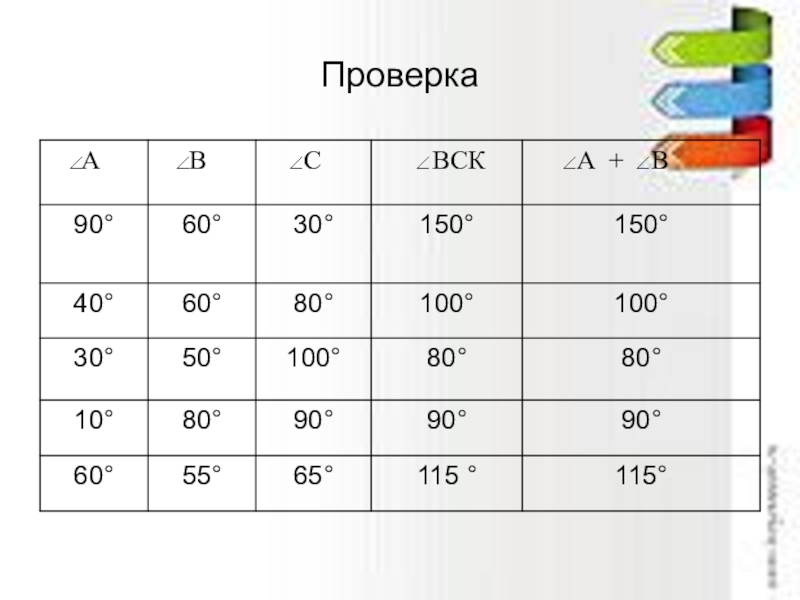
Слайд 13Какую закономерность вы заметили? (Сравните внешний угол треугольника и сумму углов
Измерьте А, В и ВСК вашего треугольника.
Сравните результат, сделайте вывод.
А
А
В
С
К
Слайд 14Составление кластера
Кластер (англ. «сluster» - скопление) – объединение нескольких однородных элементов,
Кластеры – рисуночная форма, суть которой заключается в том, что в середине листа записывается или зарисовывается основное слово (идея, тема), а по сторонам от него фиксируются идеи (слова, рисунки), с ним связанные.
Слайд 15Задание: составить кластер по теме «Виды треугольников»
Сначала данную работу учащиеся выполняют
Затем читают п.31 учебника «Остроугольный, прямоугольный и тупоугольный треугольники» и продолжают работу по составлению кластера, это позволит сделать кластер более полным.
Домашнее задание: Составьте кластер по теме «Прямоугольный треугольник»
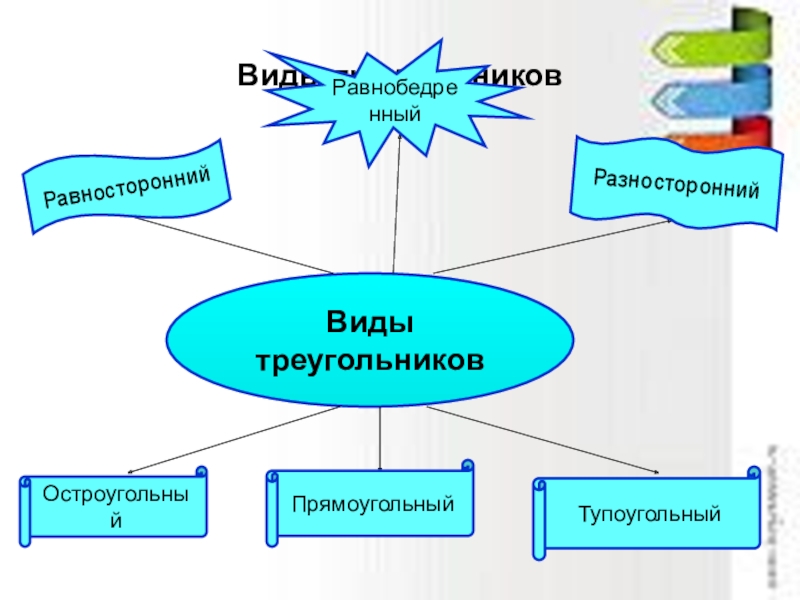
Слайд 16Виды треугольников
Виды треугольников
Равносторонний
Равнобедренный
Разносторонний
Остроугольный
Прямоугольный
Тупоугольный
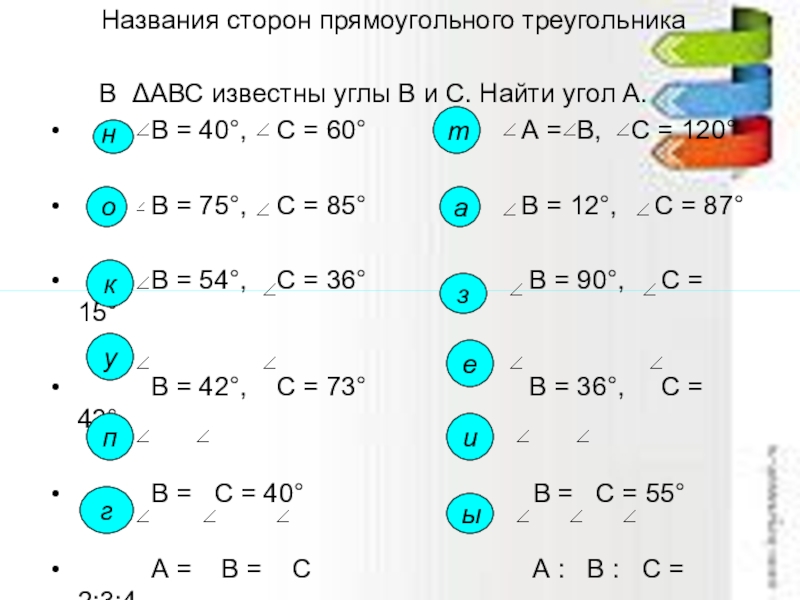
Слайд 17 В ΔАВС известны углы В и С.
В = 40°, С = 60° А = В, С = 120°
В = 75°, С = 85° В = 12°, С = 87°
В = 54°, С = 36° В = 90°, С = 15°
В = 42°, С = 73° В = 36°, С = 43°
В = С = 40° В = С = 55°
А = В = С А : В : С = 2:3:4
н
о
к
у
п
г
т
а
з
е
и
ы
Названия сторон прямоугольного треугольника
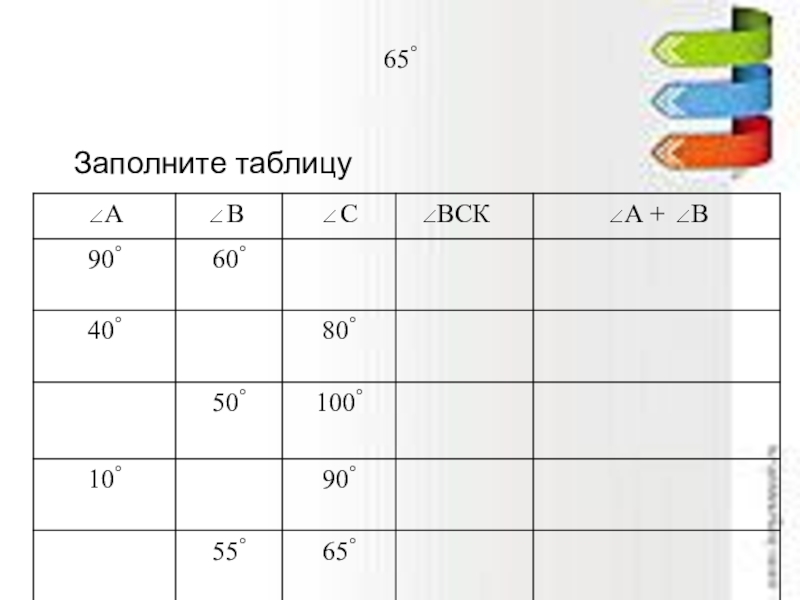
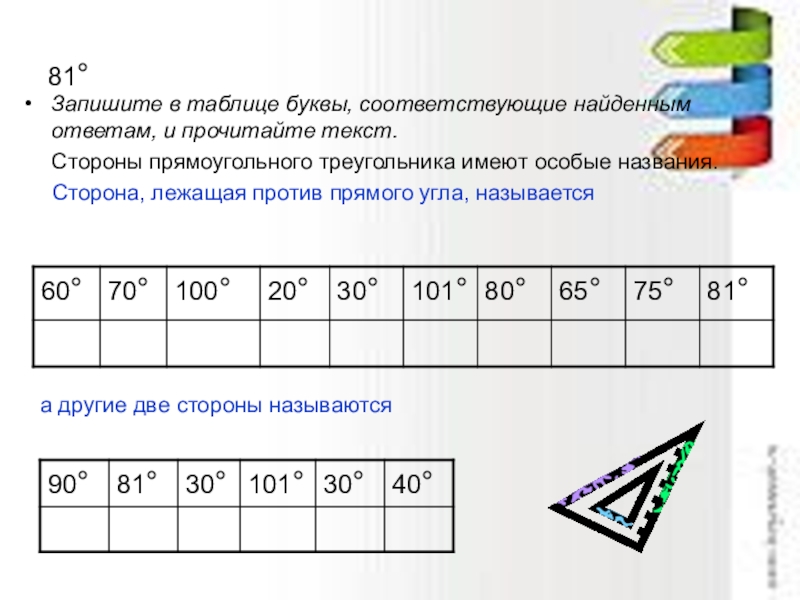
Слайд 1881°
Запишите в таблице буквы, соответствующие найденным ответам, и прочитайте текст.
Сторона, лежащая против прямого угла, называется
а другие две стороны называются
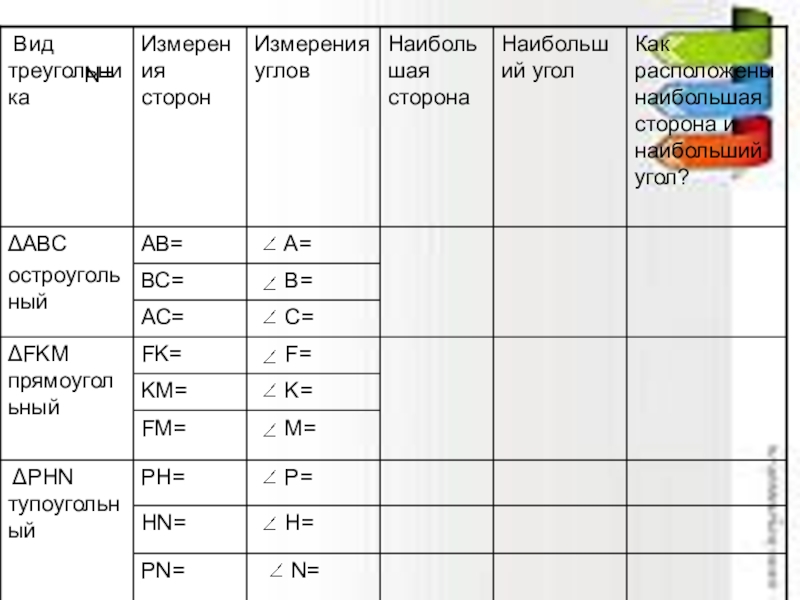
Слайд 19Лабораторная работа «Соотношения между сторонами и углами треугольника»
Цель: установить зависимость между
Задание:
1 ряд: Начертите ΔАВС – остроугольный
2 ряд: Начертите ΔFKM – прямоугольный
3 ряд: Начертите ΔPHN – тупоугольный
Измерьте стороны и углы треугольников.
Результаты измерений запишите в таблицу.
Слайд 21
Сделайте вывод о соотношении между наибольшей стороной и наибольшим углом в
Сделайте вывод о соотношении между гипотенузой и катетом в прямоугольном треугольнике.
Слайд 22Признак равнобедренного треугольника
Цель: сформулировать признак равнобедренного треугольника.
Задание:
Начертите равнобедренный ΔАВС.
А
С
В
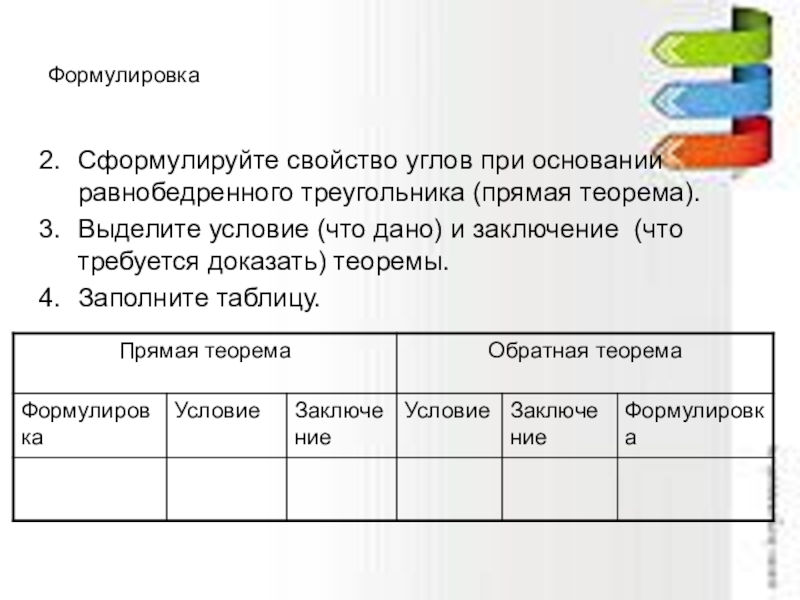
Слайд 23Формулировка
Сформулируйте свойство углов при основании равнобедренного треугольника (прямая теорема).
Выделите условие (что
Заполните таблицу.
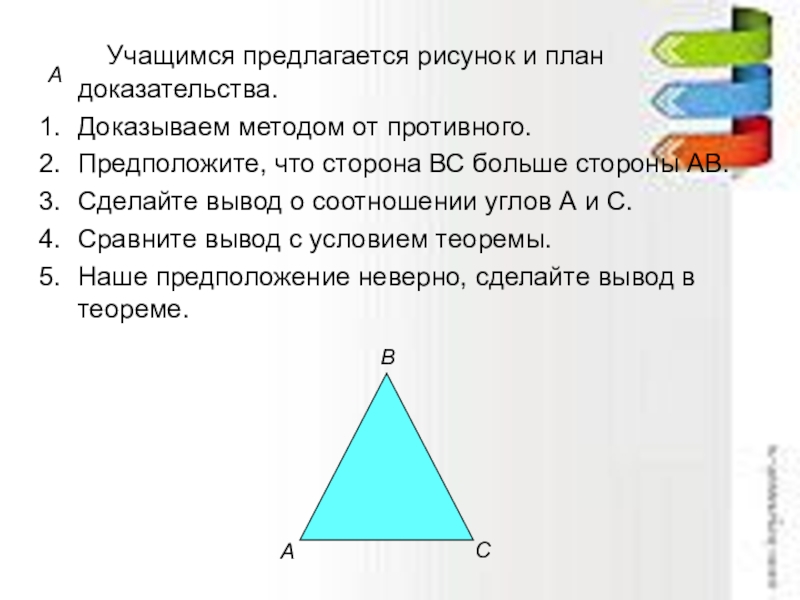
Слайд 24А
Учащимся предлагается рисунок и план доказательства.
Доказываем методом от
Предположите, что сторона ВС больше стороны АВ.
Сделайте вывод о соотношении углов А и С.
Сравните вывод с условием теоремы.
Наше предположение неверно, сделайте вывод в теореме.
А
В
С
Слайд 25Неравенство треугольника
Практическая работа
Цель: выяснить
Учащимся раздаются полоски
Зелёные длиной: 3см; 4см и 5 см
Синие длиной: 4см; 2см и 7см
Красные длиной: 4см; 2см и 6см
Задание:
Постройте 3 треугольника: зелёный, синий и красный.
Слайд 26
Сделайте вывод о существовании треугольника.
Измерьте длины сторон в зелёном треугольнике.
Выберите наибольшую
Отметьте три точки А, В и С, не лежащие на одной прямой, соедините их отрезками.
Измерьте длины отрезков АВ, АС и ВС.
Запишите неравенства для отрезков АВ, АС и ВС.
Каждое из этих неравенств называется неравенством треугольника.
Слайд 27
Знает даже младший школьник,
Что такое треугольник.
Каждый знает то, что он
Состоит из
Но совсем не каждый знает
Замечательный закон:
Сторона его большая
(Даже самая большая!)
Меньше суммы двух сторон.
Слайд 28Некоторые свойства прямоугольных треугольников
Лабораторная работа
Цель: установить зависимость между некоторыми
Оборудование: прямоугольные треугольники из белого и цветного картона, транспортир.
Работа в парах.
Задание:
Возьмите треугольники, вырезанные из белого картона. Измерьте острые углы этих треугольников и вычислите сумму их градусных мер.
Запишите результаты измерений в таблицу.
Учащиеся заполняют таблицу, изображённую на доске.
Слайд 30Лабораторная работа
Цель: определить свойство катета прямоугольного треугольника, лежащего против
Задание:
Возьмите цветные треугольники, измерьте длину гипотенузы и катета, лежащего против угла в 30°.
Результаты измерений запишите в таблицу, изображённую на доске.
Слайд 32
Поднимите каждый свой треугольник. Легко заметить, что у каждого из вас
Учащимся выдаётся второй треугольник, равный данному.
Составьте план доказательства теоремы, пользуясь учебником, стр.76.
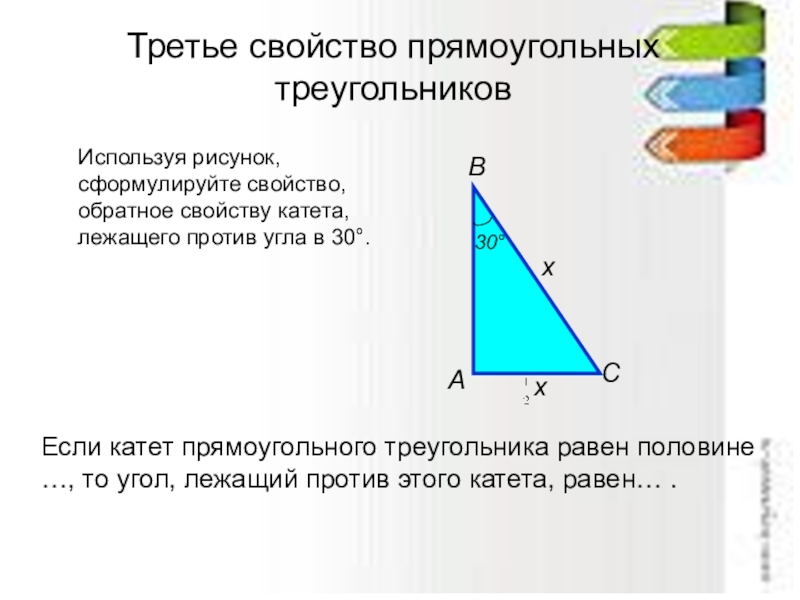
Слайд 34Третье свойство прямоугольных треугольников
Используя рисунок, сформулируйте свойство, обратное
А
В
С
30°
x
x
Если катет прямоугольного треугольника равен половине
…, то угол, лежащий против этого катета, равен… .
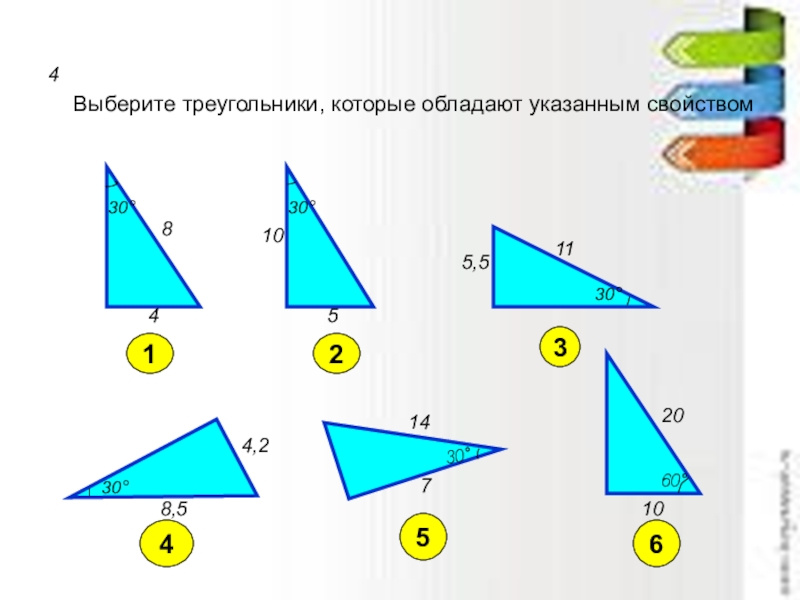
Слайд 354
Выберите треугольники, которые обладают указанным свойством
4
8
5
10
5,5
11
1
2
3
4,2
8,5
14
7
10
20
4
5
6
30°
30°
30°
30°
30°
60°
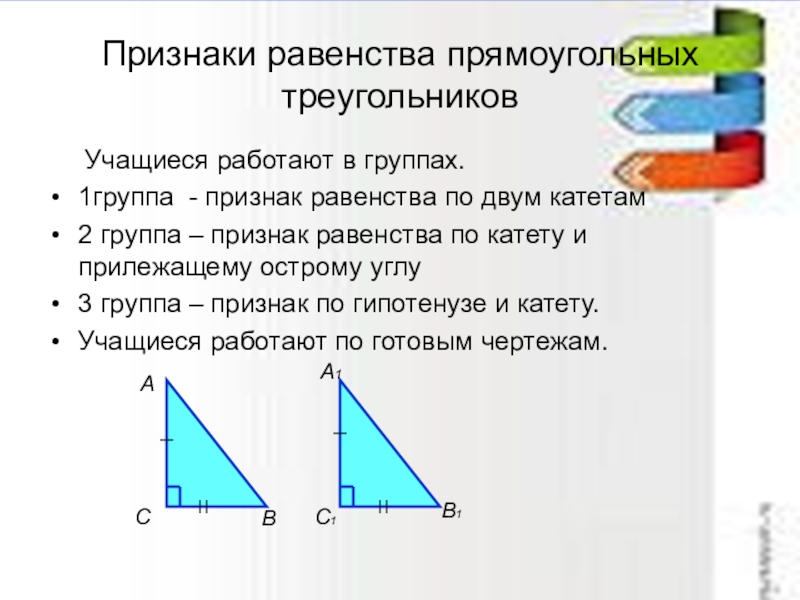
Слайд 36Признаки равенства прямоугольных треугольников
Учащиеся работают в группах.
1группа -
2 группа – признак равенства по катету и прилежащему острому углу
3 группа – признак по гипотенузе и катету.
Учащиеся работают по готовым чертежам.
А
С
В
А1
С1
В1
Слайд 37
Задание:
Сформулируй теорему.
Выполни рисунок.
Запиши, что дано, что требуется доказать в теореме.
Докажи
После работы в группах, обсуждаем доказательство каждого признака
Слайд 38
По готовому чертежу формулируем признак равенства прямоугольных треугольников по гипотенузе и
Его доказательство можно рассмотреть, используя ЭОР
Слайд 39 Синквейн – стих по математике
Выразить свои чувства, мысли,
Слайд 40Правила написания «синквейна»
Первая строка – слово (существительное, местоимение), обозначающее объект или
Во второй строке – два слова (прилагательные, причастия) для описания признаков и свойств выбранного объекта.
Третья строка – три глагола, описывающие характерные действия над объектом.
Четвертая строка – фраза из четырех слов, выражающая личное отношение автора синквейна к описываемому объекту.
В пятой строке содержится одно слово, характеризующее суть объекта.
Слайд 41Прямоугольный треугольник
Равнобедренный, равный.
Чертить, доказывать, находить углы.
Длина гипотенузы больше катета.
Фигура.
Слайд 42Расстояние от точки до прямой
Проблемная ситуация
Вы
А
.
Слайд 43Инструкция для учащихся
1. Используя предметный указатель учебника, повторите:
Какие
Что называют перпендикуляром, проведённым из данной точки к данной прямой?
Сколько перпендикуляров можно провести из точки, не лежащей на данной прямой, к данной пря мой?
Слайд 44А
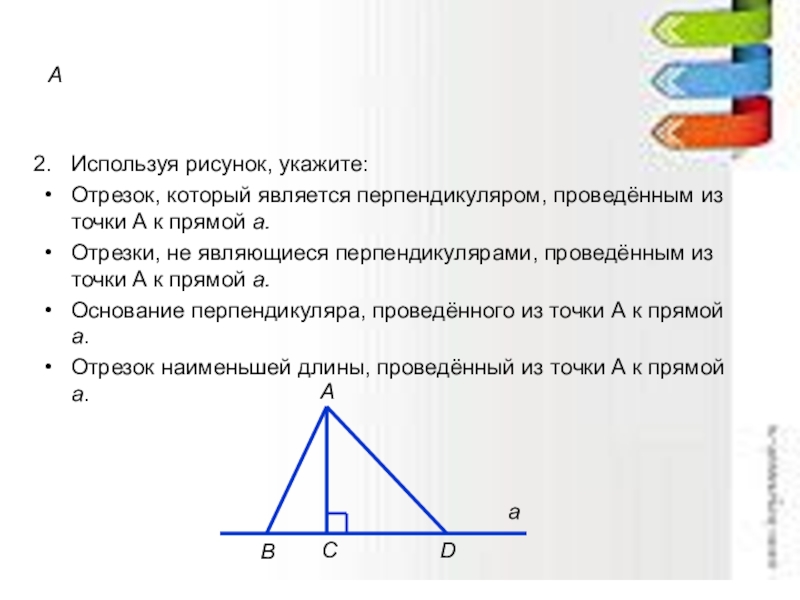
Используя рисунок, укажите:
Отрезок, который является перпендикуляром, проведённым из точки А к
Отрезки, не являющиеся перпендикулярами, проведённым из точки А к прямой а.
Основание перпендикуляра, проведённого из точки А к прямой а.
Отрезок наименьшей длины, проведённый из точки А к прямой a.
А
В
С
D
a
Слайд 45
3. Сделайте записи:
АС – перпендикуляр, АВ, АD – наклонные.
Сравните длину перпендикуляра
Сделайте вывод о длине перпендикуляра, проведённого из точки к прямой, и длине наклонной, проведённой из той же точки к этой прямой.
Длина перпендикуляра, проведённого из точки к прямой называется расстоянием от точки до прямой.
Запишите определение в тетрадь: «Расстояние от точки до прямой – это…»
Слайд 46Основные приёмы, использованные при изучении темы
Лабораторная работа;
Практическая работа;
Доказательство теоремы с пропусками;
Доказательство
Работа с учебником;
Работа с алгоритмом;
Задания по готовым чертежам;
Зашифрованные задания;
Работа с ЭОР;
Составление кластера;
Составление синквейна
Слайд 47
Видишь ли у нас тут надо
бежать изо всех сил, чтобы
оставаться на
А если хочешь попасть куда-
нибудь, надо бежать ещё
быстрее.
Льюис Кэррол
«Алиса в стране чудес»