- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по теме: Элементы симметрии в правильных многогранниках
Содержание
- 1. Презентация по теме: Элементы симметрии в правильных многогранниках
- 2. Правильные многогранники Выпуклые многогранник называется правильным ,если
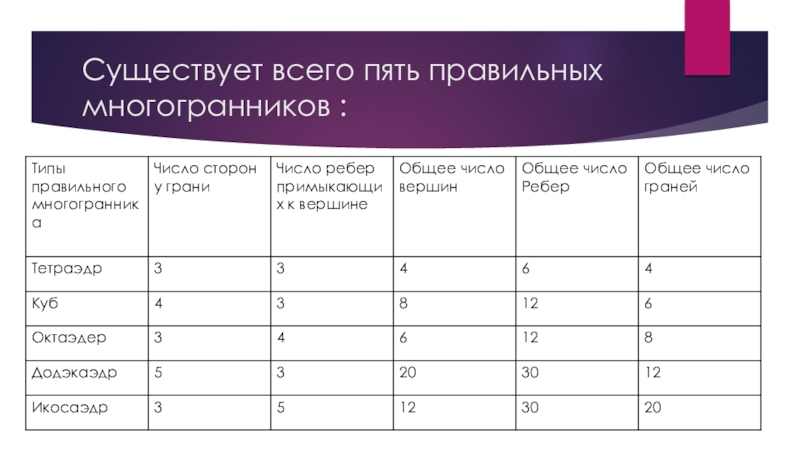
- 3. Существует всего пять правильных многогранников :
- 4. Правильный тетраэдрПравильный тетраэдр составлен из четырех равносторонних
- 5. Элементы симметрии Тетраэдр имет три оси симметрии и шесть пплоскостей ,но не иимеет центра симметрии.
- 6. Оси симметрии тетраэдраПрямая проходящая через середину двух противоположных ребер,является его осью симметрии.
- 7. Плоскость симметрии тетраэдра.Плоскость L, ппроходящая через ребро
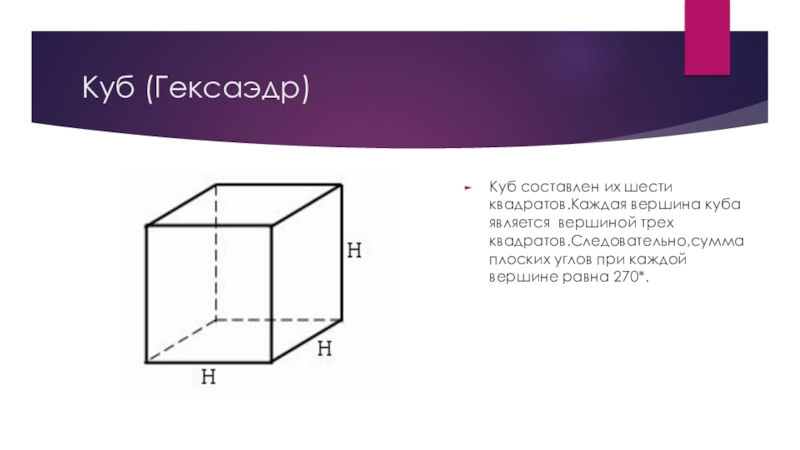
- 8. Куб (Гексаэдр)Куб составлен их шести квадратов.Каждая вершина
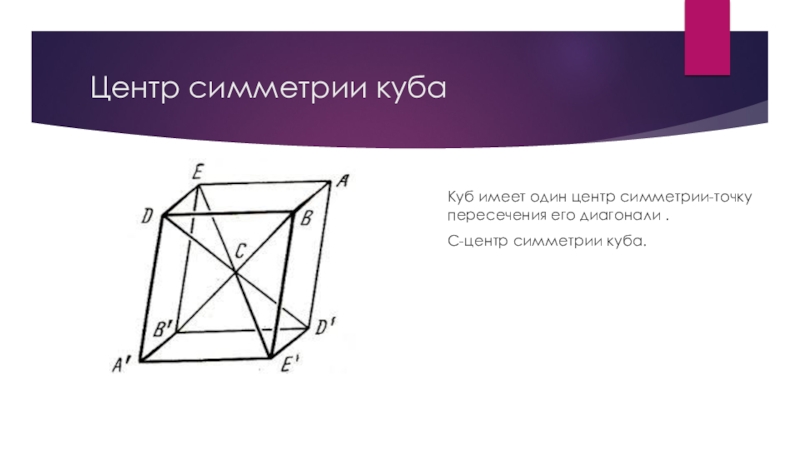
- 9. Центр симметрии кубаКуб имеет один центр симметрии-точку пересечения его диагонали .С-центр симметрии куба.
- 10. Оси симметрии кубаПрямые а и b проходящие
- 11. Плоскость симметрии кубаПлоскость симметрии куба является плоскостью,проходящая
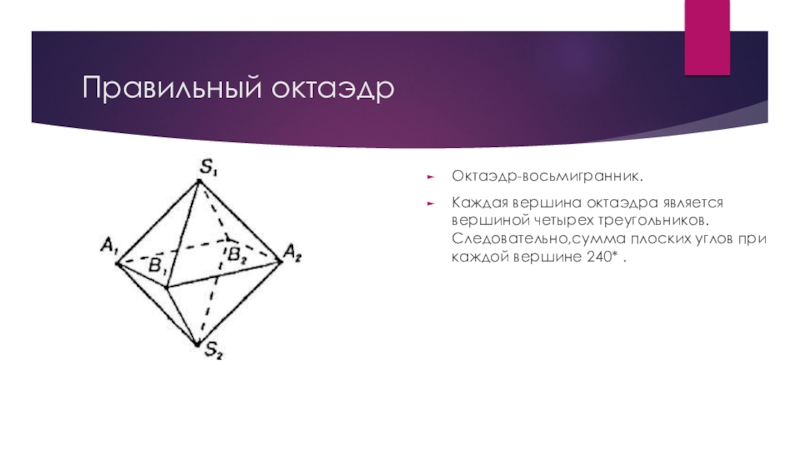
- 12. Правильный октаэдрОктаэдр-восьмигранник.Каждая вершина октаэдра является вершиной четырех треугольников. Следовательно,сумма плоских углов при каждой вершине 240* .
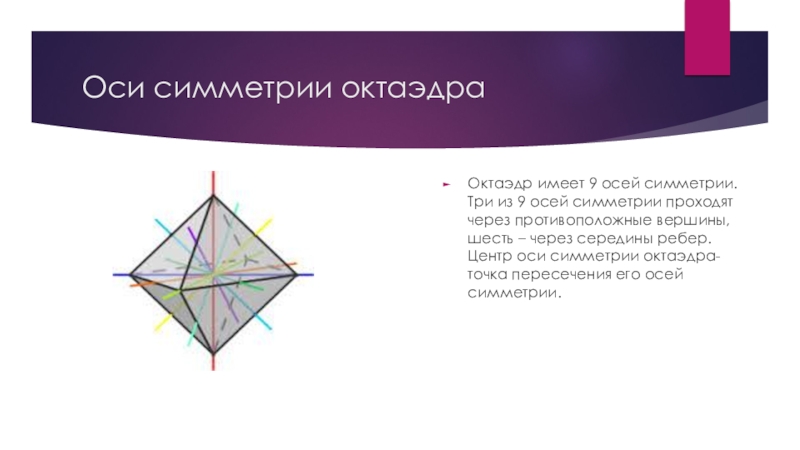
- 13. Оси симметрии октаэдраОктаэдр имеет 9 осей симметрии.
- 14. Плоскость симметрии октаэдраОктаэдр имеет 9 плоскостей симметрии.
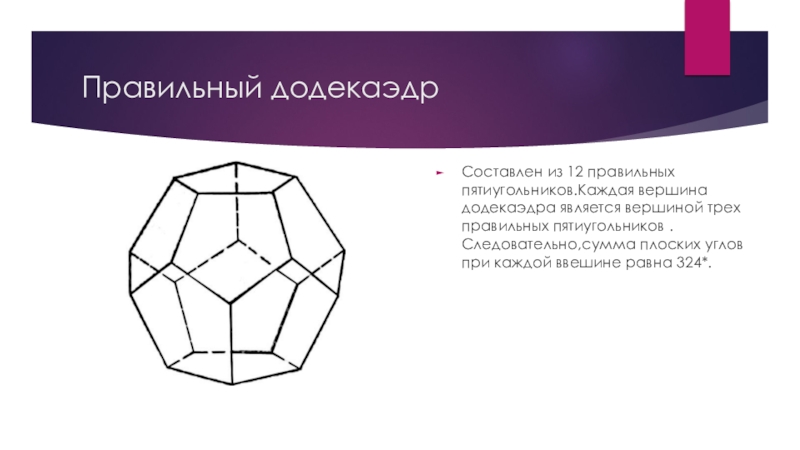
- 15. Правильный додекаэдрСоставлен из 12 правильных пятиугольников.Каждая вершина
- 16. Элементы симметрии додэкаэдраДодэкайдер имеет 15 осей симметрии и 15 плоскостей симметрии.
- 17. Правильный икосаэдрСоставлен из 20 треугольников. Каждая вершина
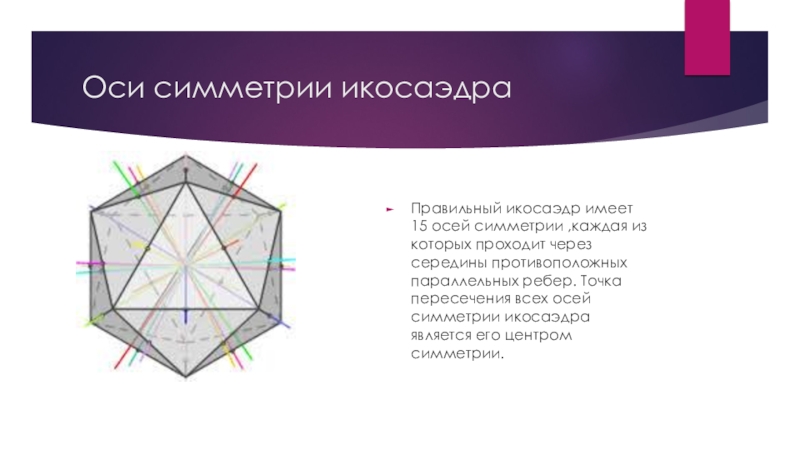
- 18. Оси симметрии икосаэдраПравильный икосаэдр имеет 15 осей
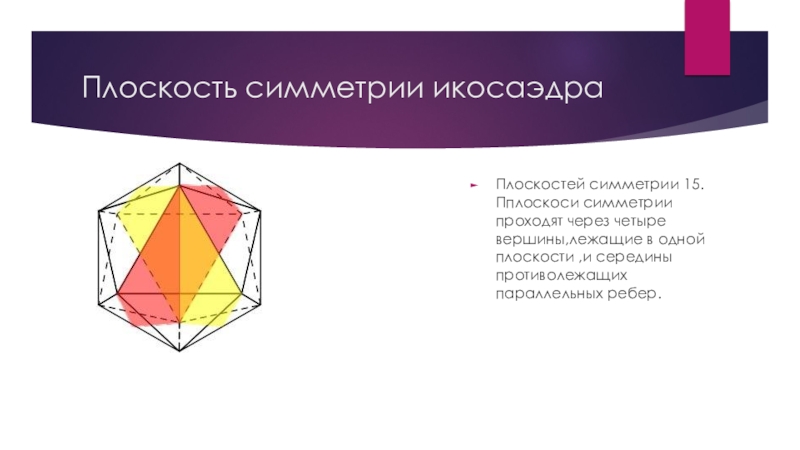
- 19. Плоскость симметрии икосаэдраПлоскостей симметрии 15. Пплоскоси симметрии
Правильные многогранники Выпуклые многогранник называется правильным ,если все его грани –равные правильные многоугольники и в каждой его вершине сходится одно и тоже число ребер .
Слайд 2Правильные многогранники
Выпуклые многогранник называется правильным ,если все его грани –равные
правильные многоугольники и в каждой его вершине сходится одно и тоже число ребер .
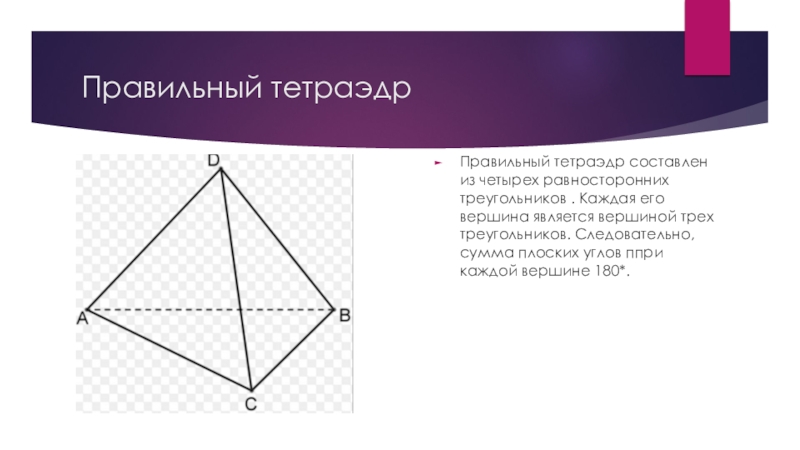
Слайд 4Правильный тетраэдр
Правильный тетраэдр составлен из четырех равносторонних треугольников . Каждая его
вершина является вершиной трех треугольников. Следовательно,сумма плоских углов ппри каждой вершине 180*.
Слайд 5Элементы симметрии
Тетраэдр имет три оси симметрии и шесть пплоскостей ,но
не иимеет центра симметрии.
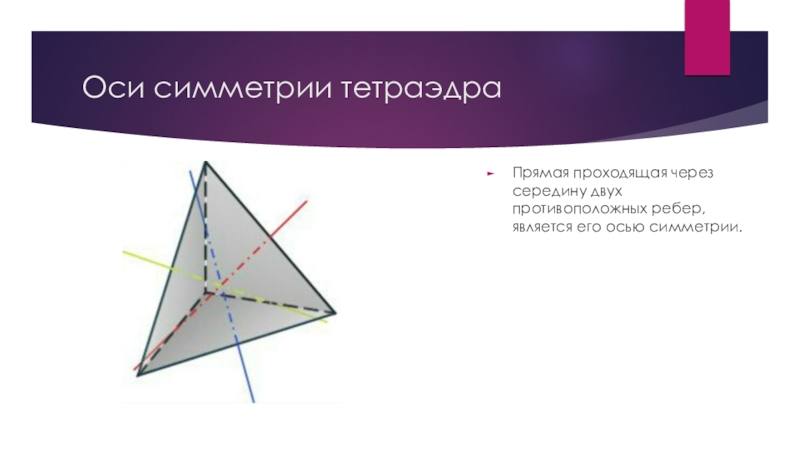
Слайд 6Оси симметрии тетраэдра
Прямая проходящая через середину двух противоположных ребер,является его осью
симметрии.
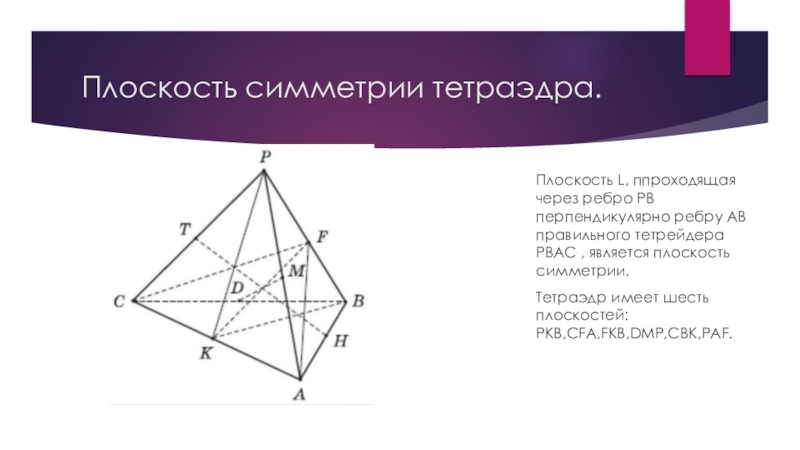
Слайд 7Плоскость симметрии тетраэдра.
Плоскость L, ппроходящая через ребро РВ перпендикулярно ребру АВ
правильного тетрейдера РВАС , является плоскость симметрии.
Тетраэдр имеет шесть плоскостей: PKB,CFA,FKB,DMP,CBK,PAF.
Тетраэдр имеет шесть плоскостей: PKB,CFA,FKB,DMP,CBK,PAF.
Слайд 8Куб (Гексаэдр)
Куб составлен их шести квадратов.Каждая вершина куба является вершиной трех
квадратов.Следовательно,сумма плоских углов при каждой вершине равна 270*.
Слайд 9 Центр симметрии куба
Куб имеет один центр симметрии-точку пересечения его диагонали
.
С-центр симметрии куба.
С-центр симметрии куба.
Слайд 10Оси симметрии куба
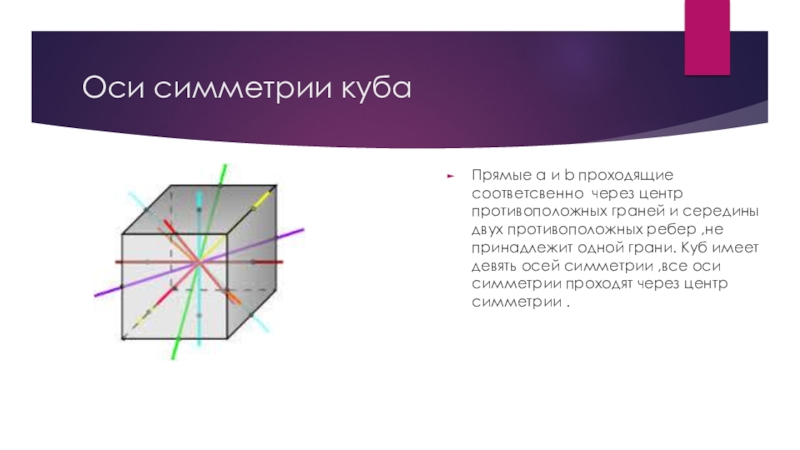
Прямые а и b проходящие соответсвенно через центр противоположных
граней и середины двух противоположных ребер ,не принадлежит одной грани. Куб имеет девять осей симметрии ,все оси симметрии проходят через центр симметрии .
Слайд 11Плоскость симметрии куба
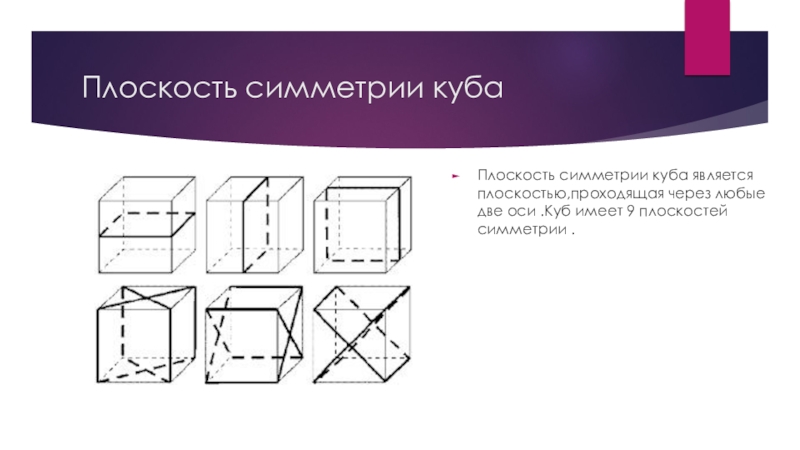
Плоскость симметрии куба является плоскостью,проходящая через любые две оси
.Куб имеет 9 плоскостей симметрии .
Слайд 12Правильный октаэдр
Октаэдр-восьмигранник.
Каждая вершина октаэдра является вершиной четырех треугольников. Следовательно,сумма плоских углов
при каждой вершине 240* .
Слайд 13Оси симметрии октаэдра
Октаэдр имеет 9 осей симметрии. Три из 9 осей
симметрии проходят через противоположные вершины,шесть – через середины ребер.Центр оси симметрии октаэдра-точка пересечения его осей симметрии.
Слайд 14Плоскость симметрии октаэдра
Октаэдр имеет 9 плоскостей симметрии. Три из 9 плоскостей
симметрии т етраэдра проходят через каждые 4 вершины октаэдра , Лежащие в одной плоскости. Шесть плоскостей симметрии проходят через две вершины,не принадлежащие одной грани ,и середины противоположных ребер.
Слайд 15Правильный додекаэдр
Составлен из 12 правильных пятиугольников.Каждая вершина додекаэдра является вершиной трех
правильных пятиугольников . Следовательно,сумма плоских углов при каждой ввешине равна 324*.
Слайд 17Правильный икосаэдр
Составлен из 20 треугольников. Каждая вершина икосаэдра является вершиной пяти
треугольников.
Следовательно, сумма плоских углов и каждой вершин равна 300*.
Следовательно, сумма плоских углов и каждой вершин равна 300*.
Слайд 18Оси симметрии икосаэдра
Правильный икосаэдр имеет 15 осей симметрии ,каждая из которых
проходит через середины противоположных параллельных ребер. Точка пересечения всех осей симметрии икосаэдра является его центром симметрии.
Слайд 19Плоскость симметрии икосаэдра
Плоскостей симметрии 15. Пплоскоси симметрии проходят через четыре вершины,лежащие
в одной плоскости ,и середины противолежащих параллельных ребер.