- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по теме Четырехугольники
Содержание
- 1. Презентация по теме Четырехугольники
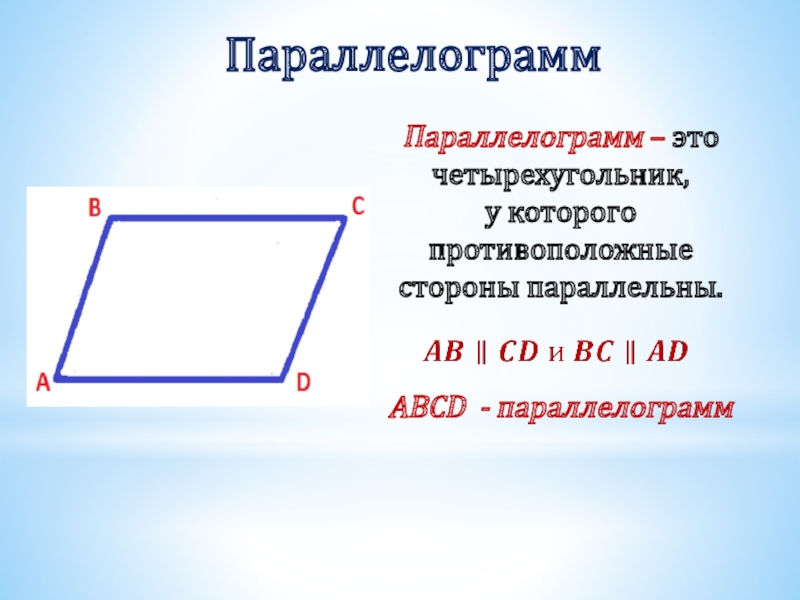
- 2. ПараллелограммABCD - параллелограмм
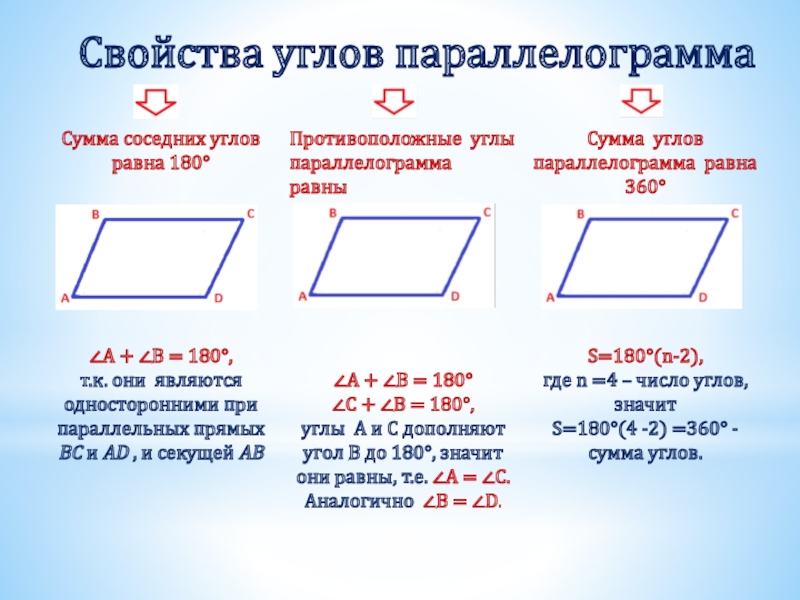
- 3. Свойства углов параллелограмма
- 4. Свойство сторон параллелограммаПротивоположные стороны параллелограмма равны.Проведем диагональ
- 5. Свойство диагоналей параллелограммаДиагонали параллелограмма пересекаются и точкой
- 6. Параллелограмм. Решение задачЗадача: В параллелограмме ABCD проведена
- 7. Параллелограмм. Решение задачЗадача: Найдите стороны параллелограмма,
- 8. Параллелограмм. Решение задачЗадача: в параллелограмме ABCD
- 9. Параллелограмм. Решение задачЗадача: ABCD – параллелограмм. Высота
- 10. Решение задач по готовым чертежам с последующей самопроверкой
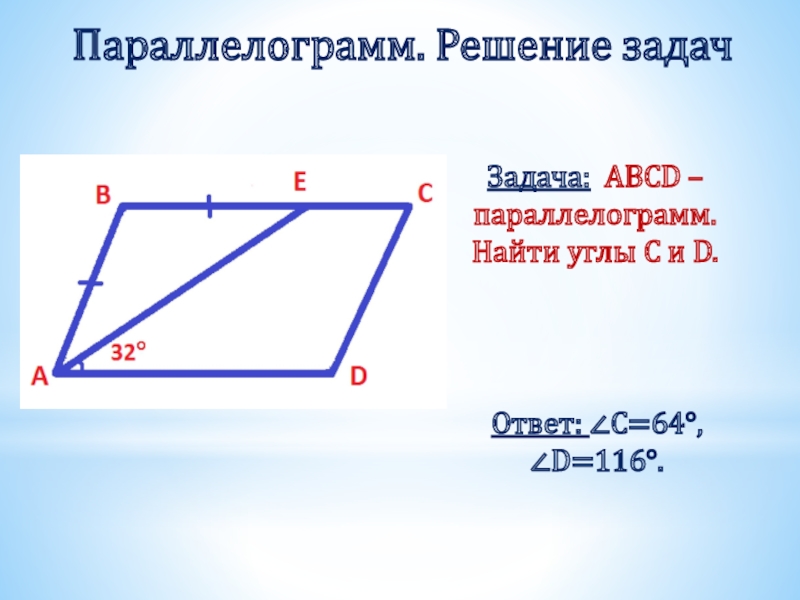
- 11. Параллелограмм. Решение задачЗадача: ABCD – параллелограмм. Найти углы C и D.Ответ: ∠C=64°,∠D=116°.
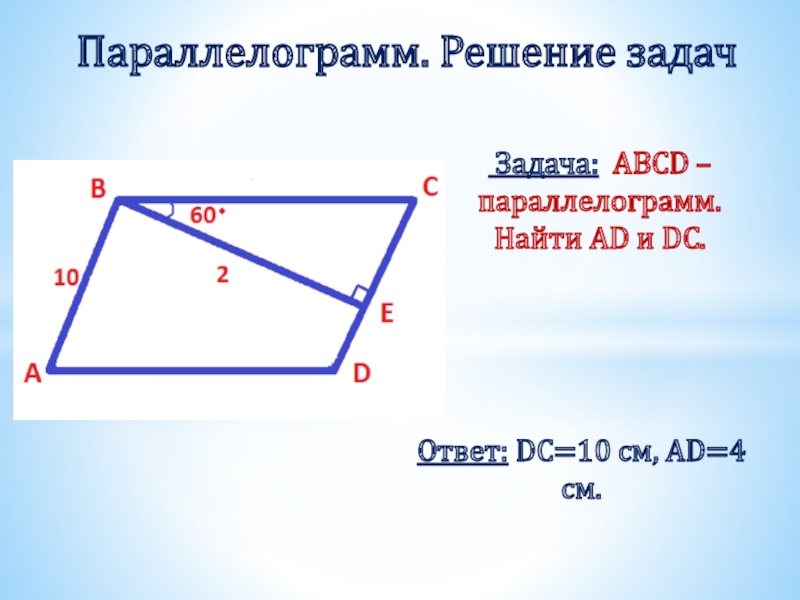
- 12. Задача: ABCD – параллелограмм. Найти AD и DC.Параллелограмм. Решение задачОтвет: DC=10 см, AD=4 см.
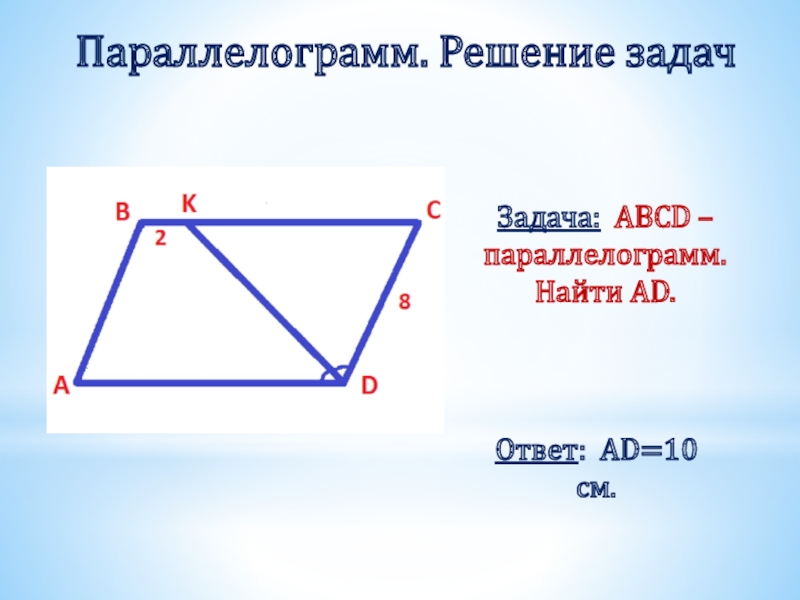
- 13. Параллелограмм. Решение задачЗадача: ABCD – параллелограмм. Найти AD.Ответ: AD=10 см.
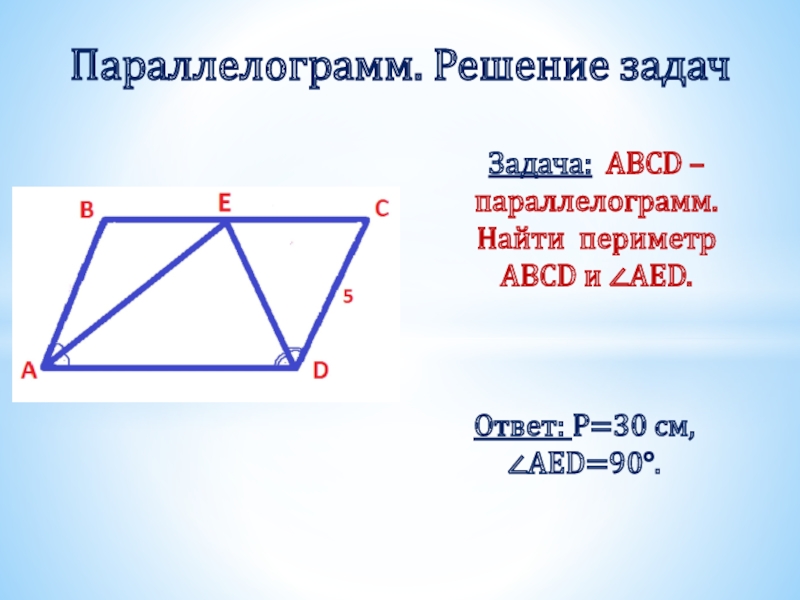
- 14. Задача: ABCD – параллелограмм. Найти периметр ABCD и ∠AED.Параллелограмм. Решение задачОтвет: Р=30 см, ∠AED=90°.
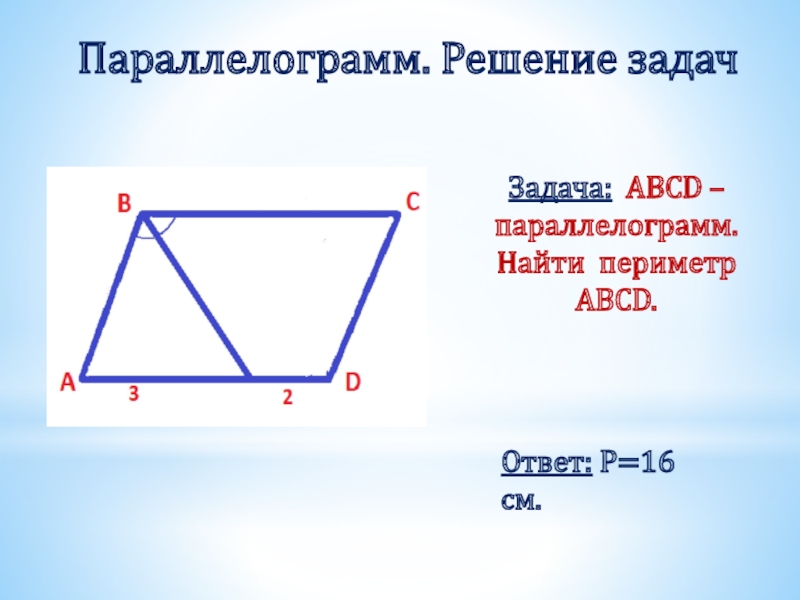
- 15. Задача: ABCD – параллелограмм. Найти периметр ABCD. Параллелограмм. Решение задачОтвет: Р=16 см.
- 16. Задача: ABCD – параллелограмм. Найти периметр ΔCOD. Параллелограмм. Решение задачОтвет: Р=28 см
- 17. ПрямоугольникПрямоугольник – это параллелограмм, у которого все углы прямые.∠A=∠B=∠C=∠D=90°
- 18. Свойства прямоугольникаПротивоположные стороны равныВсе углы прямыеДиагонали равныДиагонали точкой пересечения делятся пополам
- 19. Свойство диагоналей прямоугольникаДиагонали прямоугольника равны.Доказательство:Прямоугольные треугольники BAD
- 20. Прямоугольник. Решение задачЗадача: ABCD – прямоугольник. Найти ∠COD, если BD=12 см, AB=6 см.Ответ: 60°
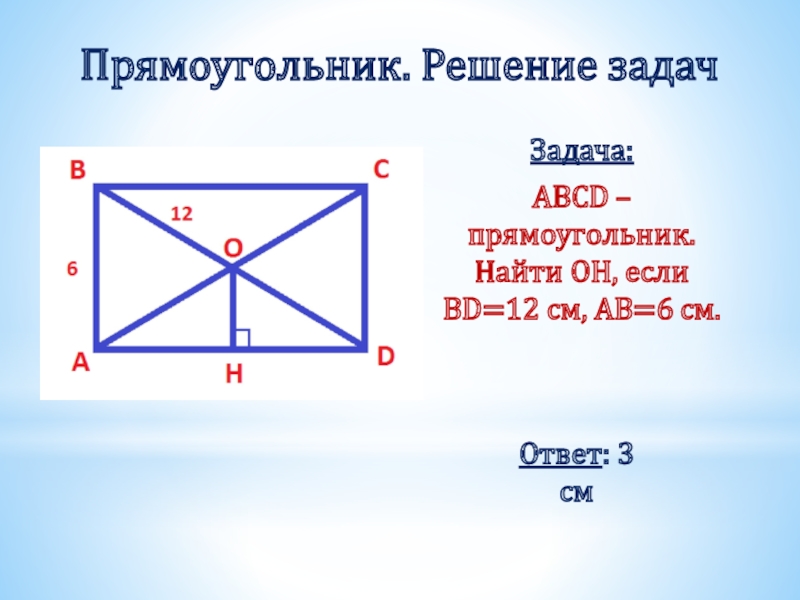
- 21. Прямоугольник. Решение задачЗадача: ABCD – прямоугольник. Найти OН, если BD=12 см, AB=6 см.Ответ: 3 см
- 22. Прямоугольник. Решение задачЗадача: ABCD – прямоугольник. АК
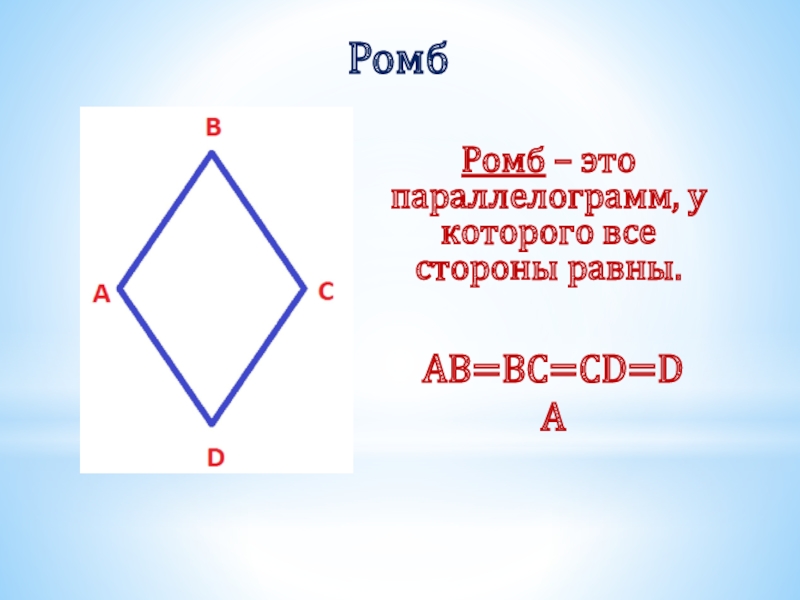
- 23. РомбРомб – это параллелограмм, у которого все стороны равны.AB=BC=CD=DA
- 24. Свойства ромбаВсе стороны равныПротивоположные углы равныДиагонали ромба перпендикулярныДиагонали ромба – биссектрисы углов ромба
- 25. Свойства диагоналей ромбаДиагонали ромба взаимно перпендикулярны и
- 26. Ромб. Решение задачЗадача: ABCD – ромб. Найдите углы ромба, если AB=ACОтвет: 60°,60°,120°,12O°
- 27. Ромб. Решение задачЗадача: ABCD – ромб. Найдите
- 28. Ромб. Решение задачЗадача: ABCD – ромб. Найдите
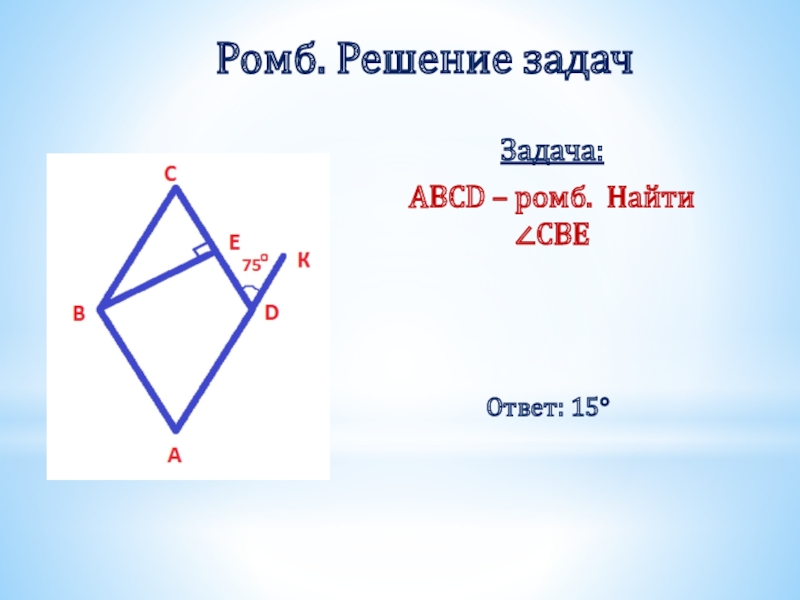
- 29. Ромб. Решение задач Задача: ABCD – ромб. Найти ∠CBE Ответ: 15°
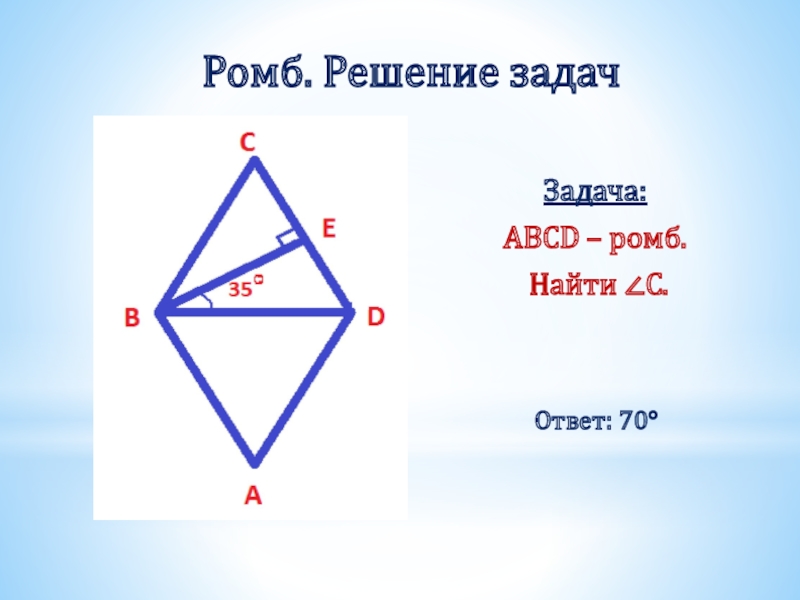
- 30. Ромб. Решение задачЗадача: ABCD – ромб. Найти ∠С.Ответ: 70°
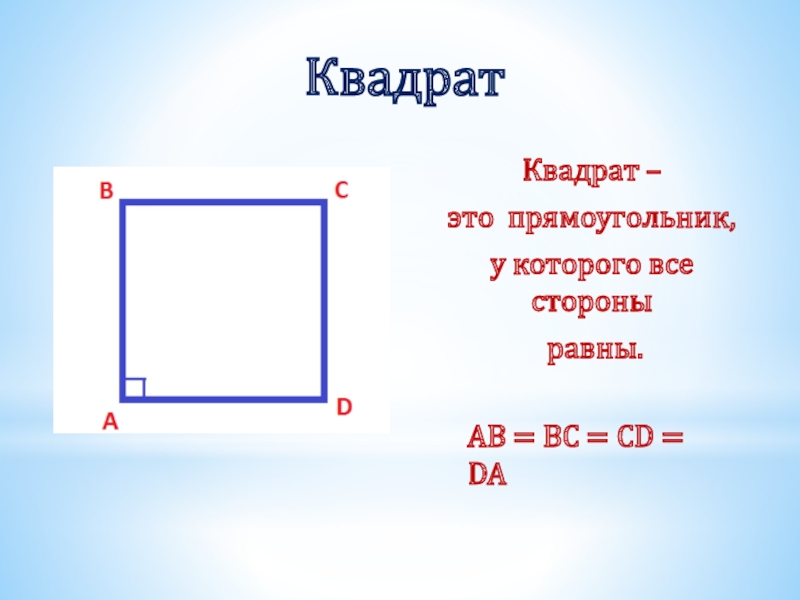
- 31. КвадратКвадрат – это прямоугольник, у которого все стороны равны.AB = BC = CD = DA
- 32. Квадрат. Свойства квадратаВсе стороны равныДиагонали равныВсе углы
Слайд 1Четырехугольники.
Свойства четырехугольников.
Решение задач
МБОУ гимназия г. Зернограда
Автор:
Якименко Виктория Владимировна,
учитель математики
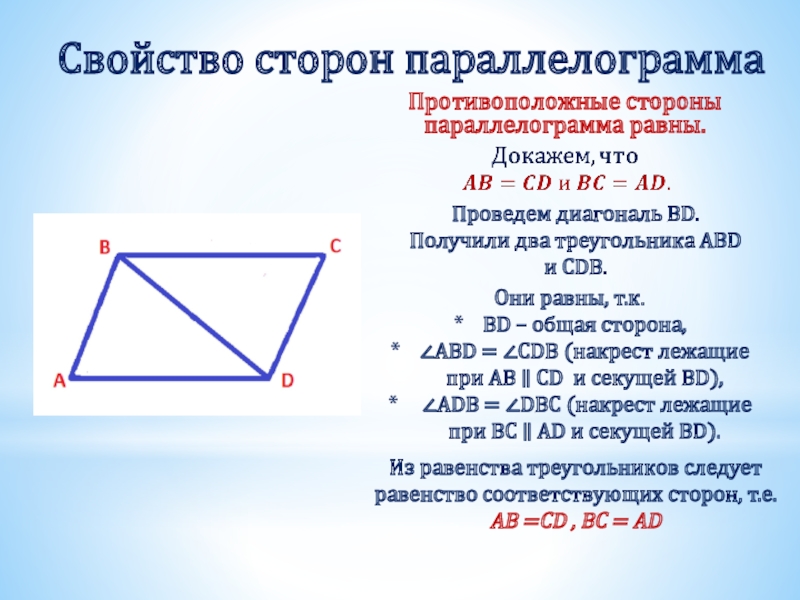
Слайд 4Свойство сторон параллелограмма
Противоположные стороны параллелограмма равны.
Проведем диагональ BD. Получили два треугольника
Они равны, т.к.
BD – общая сторона,
∠ABD = ∠CDB (накрест лежащие при AB ∥ CD и секущей BD),
∠ADB = ∠DBC (накрест лежащие при BС ∥ AD и секущей BD).
Из равенства треугольников следует равенство соответствующих сторон, т.е. AB =CD , BC = AD
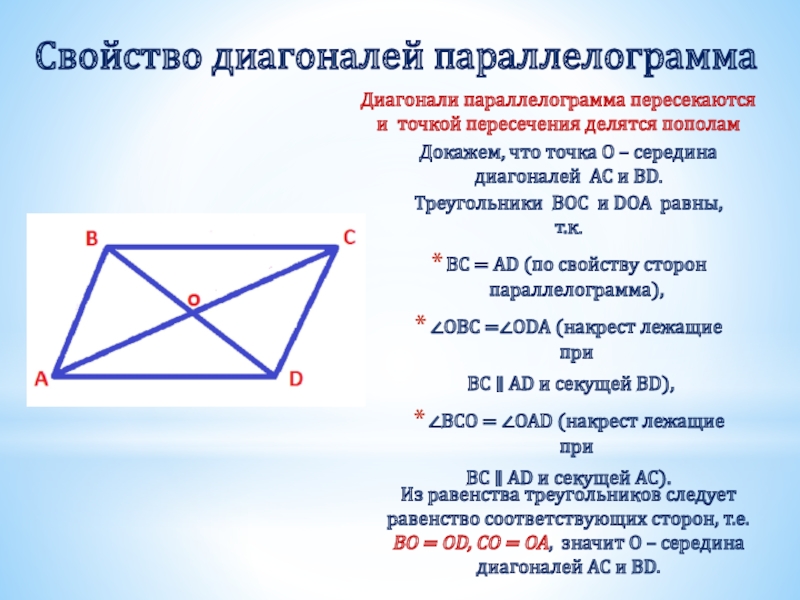
Слайд 5Свойство диагоналей параллелограмма
Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам
Докажем, что
Треугольники BOC и DOA равны, т.к.
BC = AD (по свойству сторон параллелограмма),
∠OBC =∠ODA (накрест лежащие при
BC ∥ AD и секущей BD),
∠BCO = ∠OAD (накрест лежащие при
BC ∥ AD и секущей AC).
Из равенства треугольников следует равенство соответствующих сторон, т.е. BO = OD, CO = OA, значит O – середина диагоналей AC и BD.
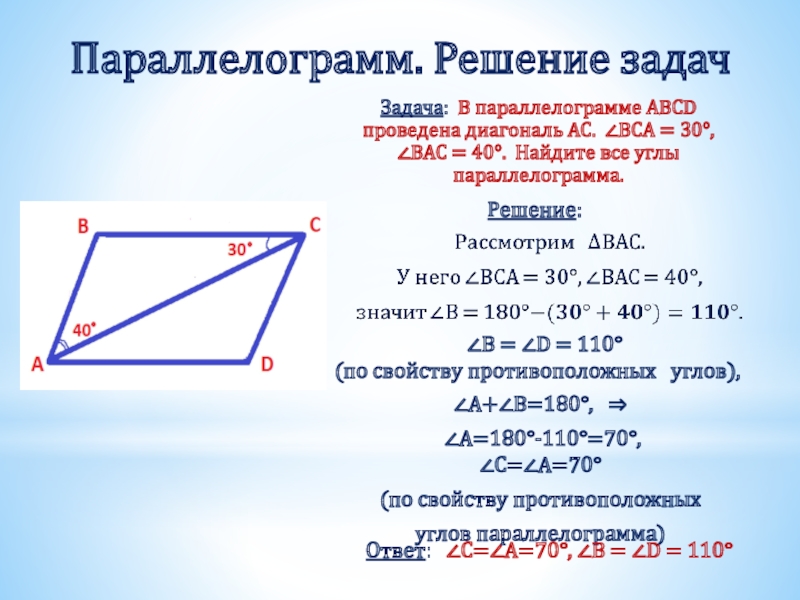
Слайд 6Параллелограмм. Решение задач
Задача: В параллелограмме ABCD проведена диагональ AC. ∠BCA =
Решение:
∠B = ∠D = 110°
(по свойству противоположных углов),
∠A+∠B=180°, ⇒
∠A=180°-110°=70°, ∠C=∠A=70°
(по свойству противоположных
углов параллелограмма)
Ответ: ∠C=∠A=70°, ∠B = ∠D = 110°
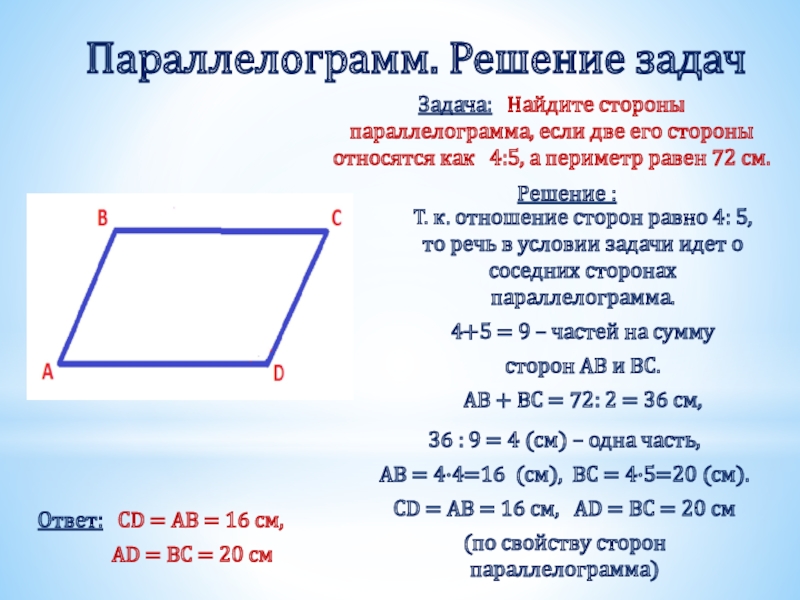
Слайд 7Параллелограмм. Решение задач
Задача: Найдите стороны параллелограмма, если две его стороны
Решение :
Т. к. отношение сторон равно 4: 5, то речь в условии задачи идет о соседних сторонах параллелограмма.
4+5 = 9 – частей на сумму
сторон AB и BC.
AB + BC = 72: 2 = 36 см,
36 : 9 = 4 (см) – одна часть,
AB = 4·4=16 (см), BC = 4·5=20 (см).
CD = AB = 16 см, AD = BC = 20 см
(по свойству сторон параллелограмма)
Ответ: CD = AB = 16 см,
AD = BC = 20 см
Слайд 8Параллелограмм. Решение задач
Задача: в параллелограмме ABCD проведена биссектриса угла А.
Решение:
∠3=∠2, т.к. АH – биссектриса,
∠1=∠3 (накрест лежащие
при BC∥AD и секущей AH), ⇒ ∠1=∠2,
ΔABH – равнобедренный ( по признаку),
⇒ AB = BH = 6cм.
BC = AD = 10 cм, AB = CD = 6 cм.
Р = 2·(10+6) = 32 см.
Ответ: P=32 см.
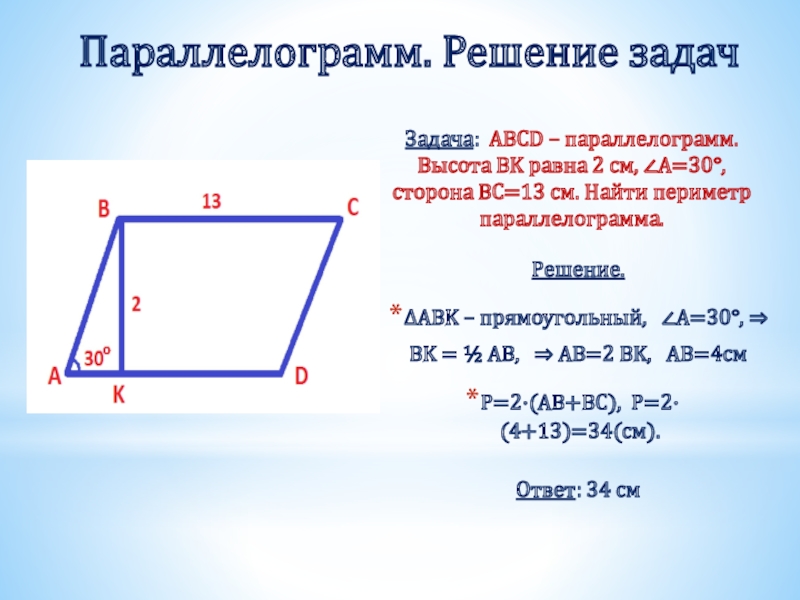
Слайд 9Параллелограмм. Решение задач
Задача: ABCD – параллелограмм. Высота BK равна 2 см,
Решение.
ΔABK – прямоугольный, ∠A=30°, ⇒
BK = ½ AB, ⇒ AB=2 BK, AB=4см
P=2·(AB+BC), Р=2·(4+13)=34(см).
Ответ: 34 см
Слайд 11Параллелограмм. Решение задач
Задача: ABCD – параллелограмм. Найти углы C и D.
Ответ:
Слайд 12 Задача: ABCD – параллелограмм. Найти AD и DC.
Параллелограмм. Решение задач
Ответ:
Слайд 14Задача: ABCD – параллелограмм. Найти периметр ABCD и ∠AED.
Параллелограмм. Решение задач
Ответ:
Слайд 15
Задача: ABCD – параллелограмм. Найти периметр ABCD.
Параллелограмм. Решение задач
Ответ: Р=16 см.
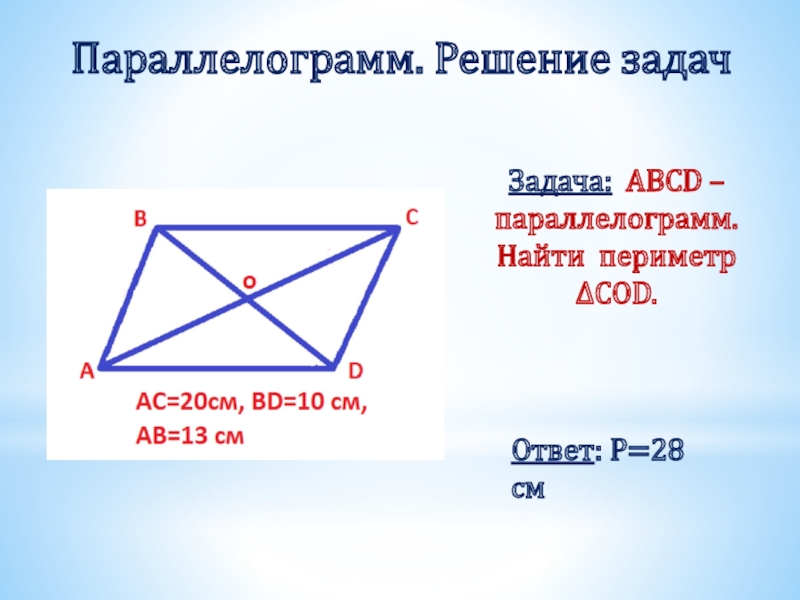
Слайд 16
Задача: ABCD – параллелограмм. Найти периметр
ΔCOD.
Параллелограмм. Решение задач
Ответ: Р=28 см
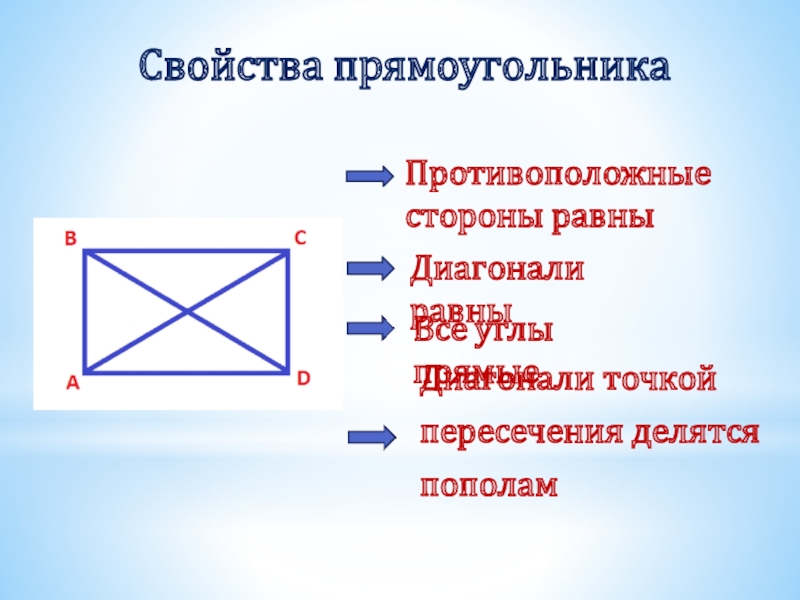
Слайд 18Свойства прямоугольника
Противоположные стороны равны
Все углы прямые
Диагонали равны
Диагонали точкой
пересечения делятся
пополам
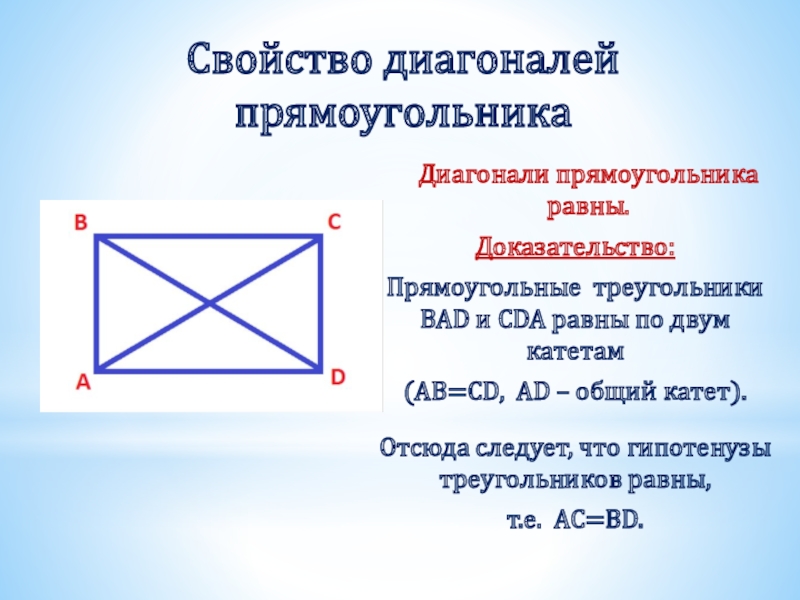
Слайд 19Свойство диагоналей прямоугольника
Диагонали прямоугольника равны.
Доказательство:
Прямоугольные треугольники BAD и CDA равны по
(AB=CD, AD – общий катет).
Отсюда следует, что гипотенузы треугольников равны,
т.е. AC=BD.
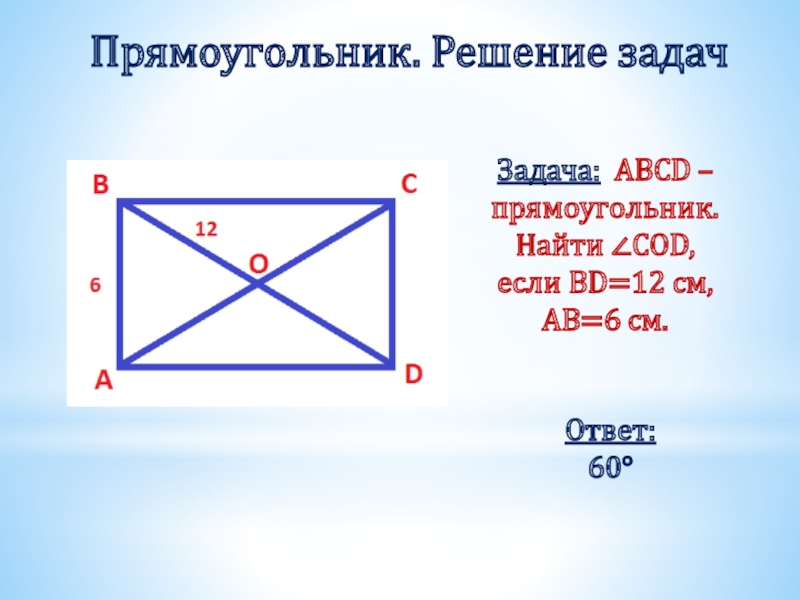
Слайд 20Прямоугольник. Решение задач
Задача: ABCD – прямоугольник. Найти ∠COD, если BD=12 см,
Ответ: 60°
Слайд 21Прямоугольник. Решение задач
Задача:
ABCD – прямоугольник. Найти OН, если BD=12 см,
Ответ: 3 см
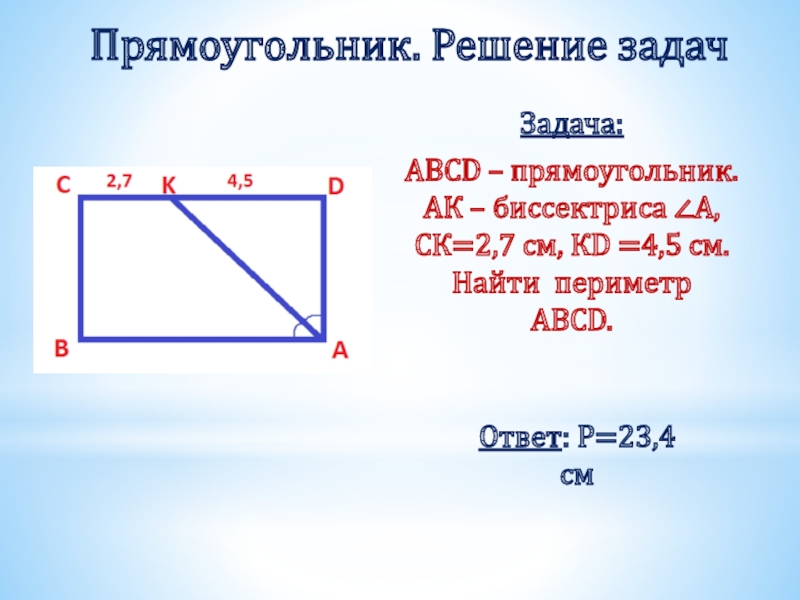
Слайд 22Прямоугольник. Решение задач
Задача:
ABCD – прямоугольник. АК – биссектриса ∠A, СК=2,7
Ответ: Р=23,4 см
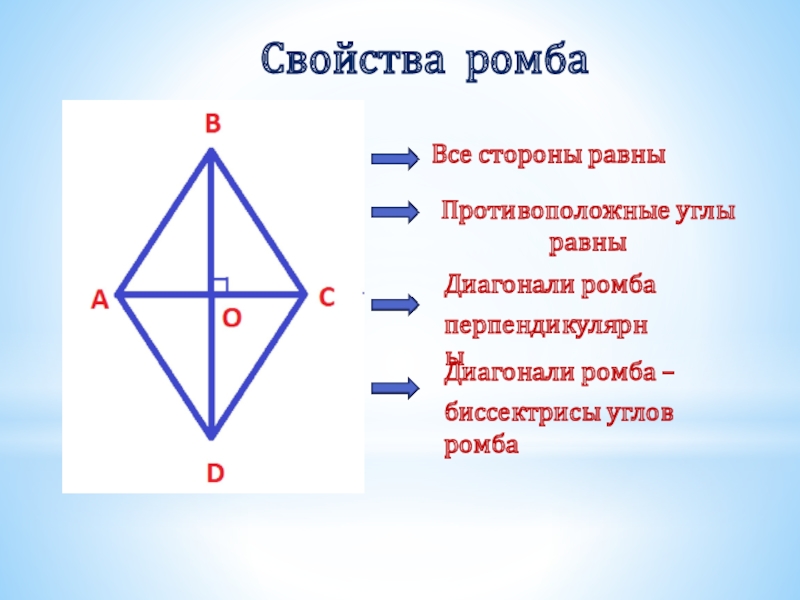
Слайд 24Свойства ромба
Все стороны равны
Противоположные углы равны
Диагонали ромба
перпендикулярны
Диагонали ромба –
биссектрисы
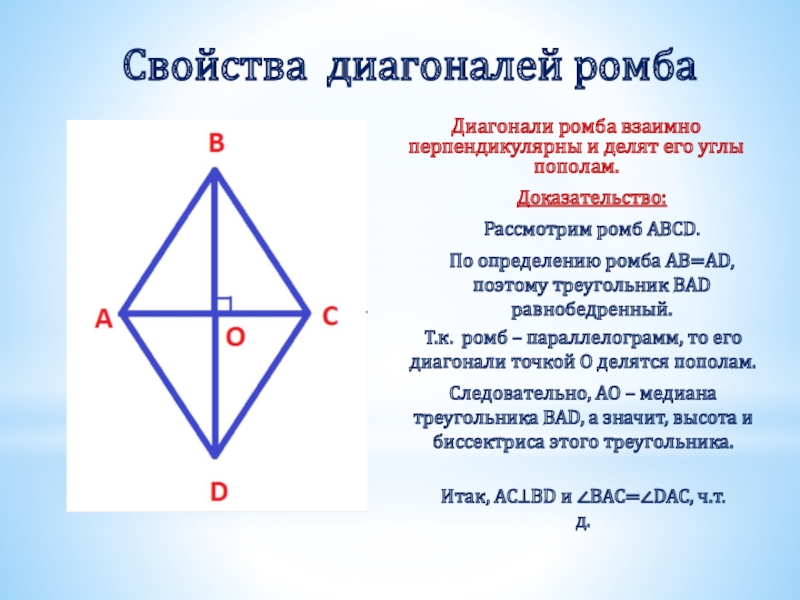
Слайд 25Свойства диагоналей ромба
Диагонали ромба взаимно перпендикулярны и делят его углы пополам.
Доказательство:
Рассмотрим
По определению ромба AB=AD, поэтому треугольник BAD равнобедренный.
Т.к. ромб – параллелограмм, то его диагонали точкой О делятся пополам.
Следовательно, АО – медиана треугольника BAD, а значит, высота и биссектриса этого треугольника.
Итак, AC⊥BD и ∠BAC=∠DAC, ч.т.д.
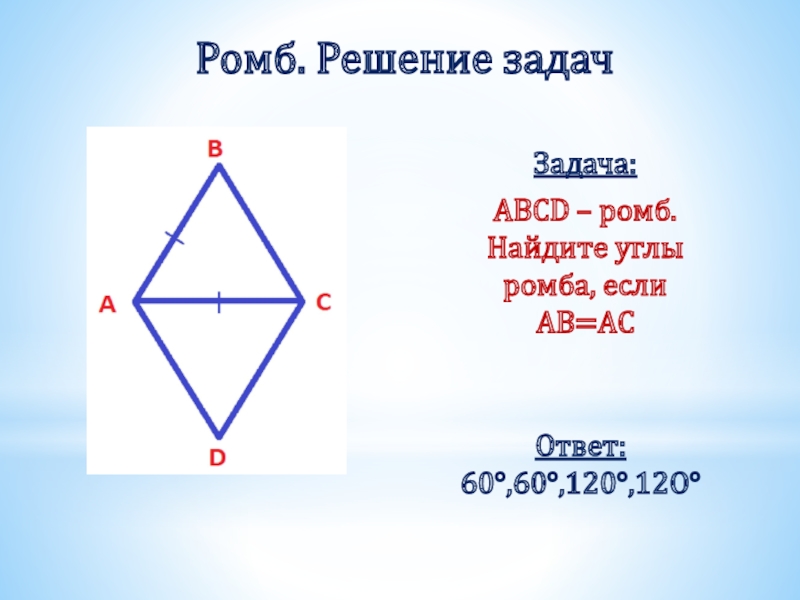
Слайд 26Ромб. Решение задач
Задача:
ABCD – ромб. Найдите углы ромба, если AB=AC
Ответ:
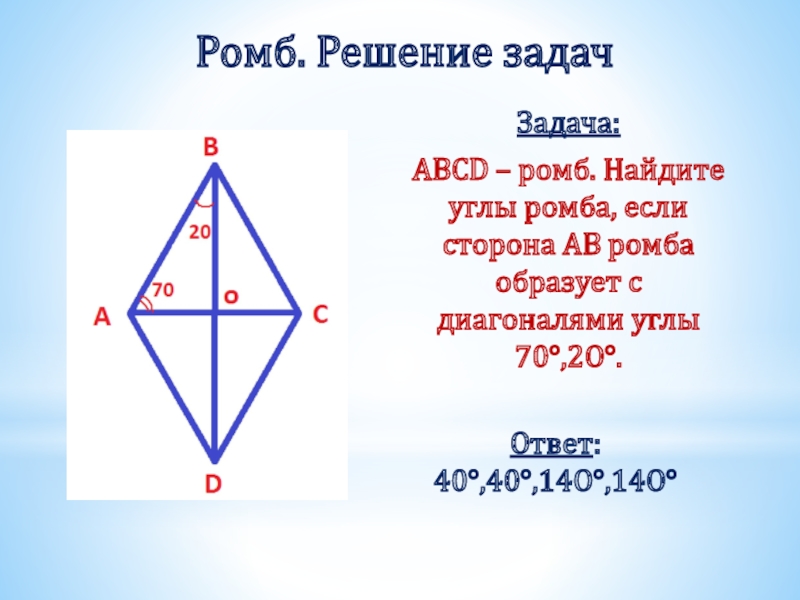
Слайд 27Ромб. Решение задач
Задача:
ABCD – ромб. Найдите углы ромба, если сторона
Ответ: 40°,40°,14O°,14O°
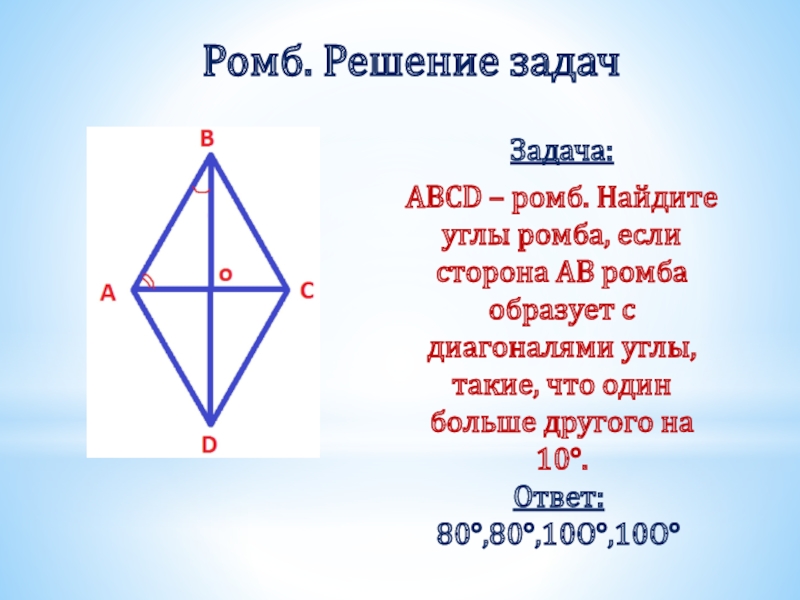
Слайд 28Ромб. Решение задач
Задача:
ABCD – ромб. Найдите углы ромба, если сторона
Ответ: 80°,80°,10O°,10O°
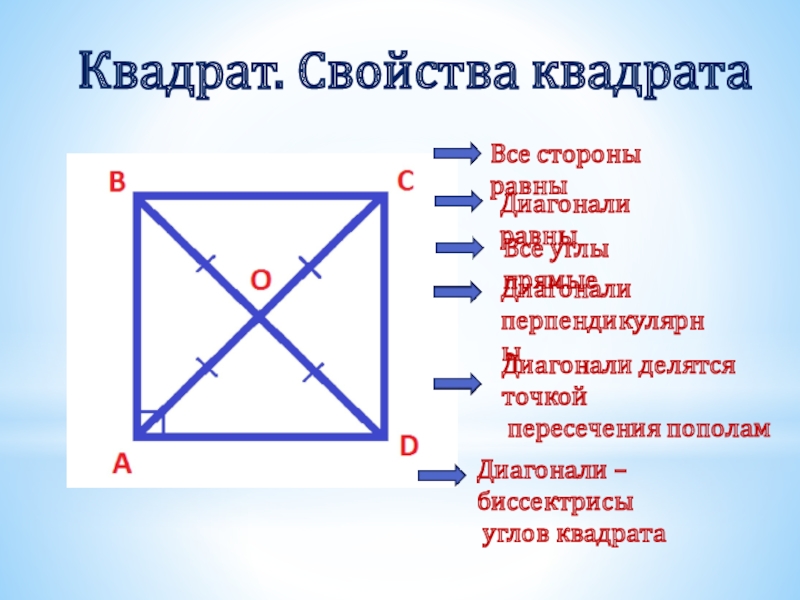
Слайд 32Квадрат. Свойства квадрата
Все стороны равны
Диагонали равны
Все углы прямые
Диагонали
перпендикулярны
Диагонали делятся точкой
Диагонали – биссектрисы
углов квадрата