- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по подготовке ГВЭ в Коррекционной школе
Содержание
- 1. Презентация по подготовке ГВЭ в Коррекционной школе
- 2. Цели работы:Выяснение существования иной, отличной от школьной программы, формулы нахождения площади решетчатого многоугольника.Области применения искомой формулы.
- 3. Введение. Математическое образование, получаемое в общеобразовательных школах, является
- 4. Задание В6. На клетчатой бумаге с клетками размером
- 5. Итак, чтобы все-таки решить это задание мне
- 6. Историческая справка. Георг Александр Пик (10 августа, 1859
- 7. Теорема Пика. Теорема Пика — классический результат комбинаторной
- 8. Доказательство теоремы Пика. Любой такой многоугольник легко разбить
- 9. Применение. Итак, вернемся к заданию В6. Теперь, зная
- 10. По той же формуле мы можем найти
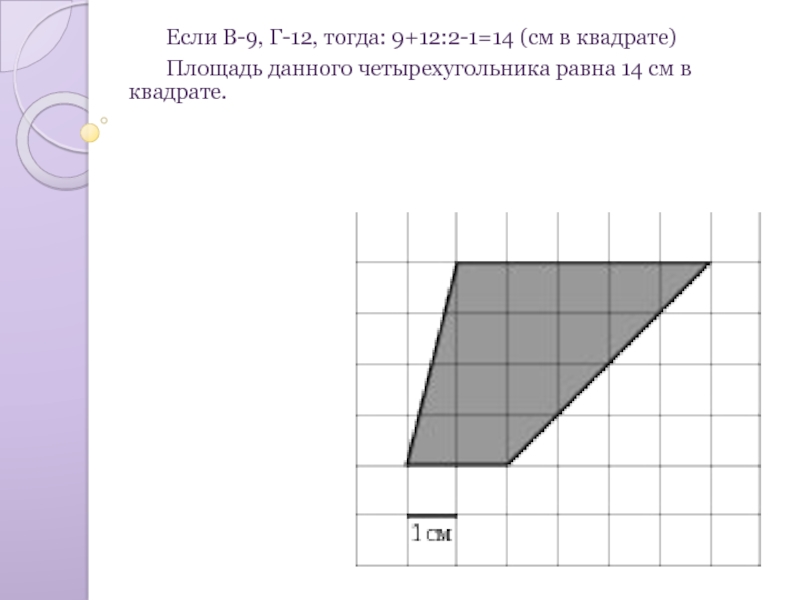
- 11. Если В-9, Г-12, тогда: 9+12:2-1=14 (см в квадрате) Площадь данного четырехугольника равна 14 см в квадрате.
- 12. Области применения формулы. Помимо того, что формула применяется
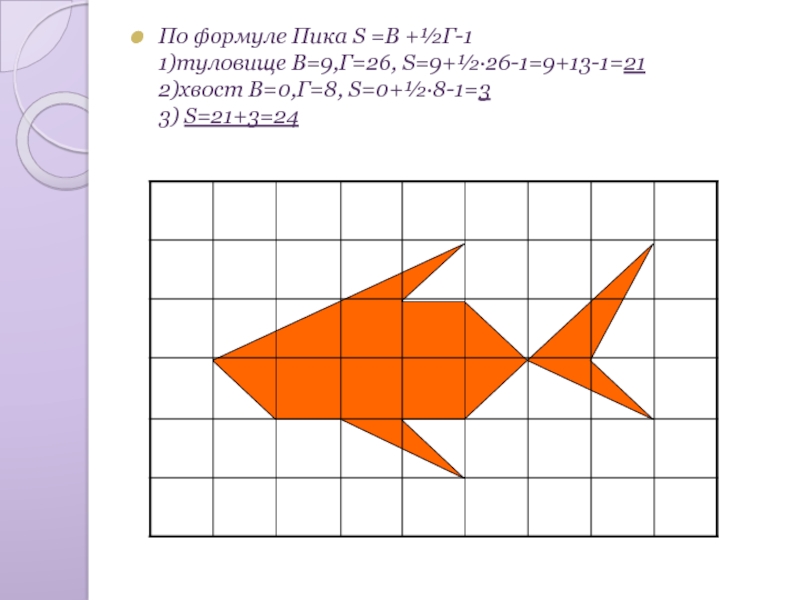
- 13. По формуле Пика S =В +½Г-1 1)туловище В=9,Г=26, S=9+½·26-1=9+13-1=21 2)хвост В=0,Г=8, S=0+½·8-1=3 3) S=21+3=24
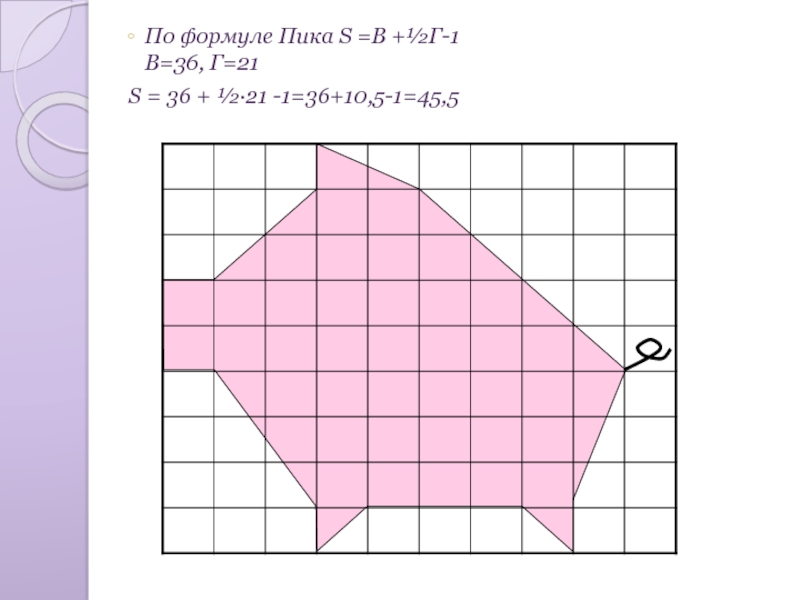
- 14. По формуле Пика S =В +½Г-1 В=36, Г=21 S = 36 + ½·21 -1=36+10,5-1=45,5
- 15. Заключение. В итоге, я пришла к выводу, что
- 16. Справочник.Многоугольник без самопересечений называется решётчатым, если все
Цели работы:Выяснение существования иной, отличной от школьной программы, формулы нахождения площади решетчатого многоугольника.Области применения искомой формулы.
Слайд 2Цели работы:
Выяснение существования иной, отличной от школьной программы, формулы нахождения площади
решетчатого многоугольника.
Области применения искомой формулы.
Области применения искомой формулы.
Слайд 3Введение.
Математическое образование, получаемое в общеобразовательных школах, является важнейшим компонентом общего образования
и общей культуры современного человека.
На данном этапе, школьная система рассчитана на одиннадцатилетнее обучение.
Всем учащимся в конце одиннадцатого класса предстоит сдавать Единый Государственный Экзамен, который покажет уровень знаний, полученный во время учебы в школе. Но школьная программа не всегда предоставляет самые рациональные способы решения каких-либо задач .
Например, просматривая результаты ЕГЭ 2010 года видно, что многие ученики теряют баллы из-за задания В6.
Я задалась целью, как же можно сэкономить время и правильно решить это задание.
На данном этапе, школьная система рассчитана на одиннадцатилетнее обучение.
Всем учащимся в конце одиннадцатого класса предстоит сдавать Единый Государственный Экзамен, который покажет уровень знаний, полученный во время учебы в школе. Но школьная программа не всегда предоставляет самые рациональные способы решения каких-либо задач .
Например, просматривая результаты ЕГЭ 2010 года видно, что многие ученики теряют баллы из-за задания В6.
Я задалась целью, как же можно сэкономить время и правильно решить это задание.
Слайд 4Задание В6.
На клетчатой бумаге с клетками размером 1 см на 1 см
изображены фигуры(см. рисунок). Найдите их площади в квадратных сантиметрах.
Слайд 5 Итак, чтобы все-таки решить это задание мне нужно применить формулы нахождения
площади, которые мы изучаем в 8классе.Но на это уйдет очень много времени, а мне нужно ответить на поставленный вопрос как можно быстрее, ведь время на экзамене строго ограниченно.
Поэтому, проведя исследования, я выяснила, что существует теорема Пика, которая в школьной программе не изучается, но которая поможет мне быстрее справиться с заданием.
Поэтому, проведя исследования, я выяснила, что существует теорема Пика, которая в школьной программе не изучается, но которая поможет мне быстрее справиться с заданием.
Слайд 6Историческая справка.
Георг Александр Пик (10 августа, 1859 - 26 июля 1942)
был австрийским математиком. Он умер в концлагере Терезин. Сегодня он известен из-за формулы Пика для определения площади решетки полигонов. Он опубликовал свою формулу в статье в 1899 году, она стала популярной, когда Хьюго Штейнгауз включил её в 1969 году в издание математических снимков.
Пик учился в Венском университете и защитил кандидатскую в 1880 году. После получения докторской степени он был назначен помощником Эрнеста Маха в Шерльско-Фердинандском университете в Праге. Он стал преподавателем там в 1881 году. Взяв отпуск в университете в 1884 году, стал работать с Феликсом Клейном в Лейпцигском университете. Он оставался в Праге до своей отставки в 1927 году, а за тем вернулся в Вену.
Пик возглавлял комитет в(тогда) немецком университете Праги, который назначил Альберта Эйнштейна профессором кафедры математической физики в 1911 году.
Пик был избран членом Чешской академии наук и искусств, но был исключен после захвата нацистами Праги.
После ухода на пенсию в 1927 году, Пик вернулся в Вену, город, где он родился. После аншлюса, когда нацисты вошли в Австрию 12 марта 1938 года, Пик вернулся в Прагу. В марте 1939 года нацисты вторглись в Чехословакию. Георг был отправлен в концентрационный лагерь Терезин 13 июля 1942. Он умер через две недели.
Пик учился в Венском университете и защитил кандидатскую в 1880 году. После получения докторской степени он был назначен помощником Эрнеста Маха в Шерльско-Фердинандском университете в Праге. Он стал преподавателем там в 1881 году. Взяв отпуск в университете в 1884 году, стал работать с Феликсом Клейном в Лейпцигском университете. Он оставался в Праге до своей отставки в 1927 году, а за тем вернулся в Вену.
Пик возглавлял комитет в(тогда) немецком университете Праги, который назначил Альберта Эйнштейна профессором кафедры математической физики в 1911 году.
Пик был избран членом Чешской академии наук и искусств, но был исключен после захвата нацистами Праги.
После ухода на пенсию в 1927 году, Пик вернулся в Вену, город, где он родился. После аншлюса, когда нацисты вошли в Австрию 12 марта 1938 года, Пик вернулся в Прагу. В марте 1939 года нацисты вторглись в Чехословакию. Георг был отправлен в концентрационный лагерь Терезин 13 июля 1942. Он умер через две недели.
Слайд 7Теорема Пика.
Теорема Пика — классический результат комбинаторной геометрии и геометрии чисел.
Площадь
многоугольника с целочисленными вершинами равна сумме
В + Г/2 – 1,
где В есть количество целочисленных точек внутри многоугольника, а Г количество целочисленных точек на границе многоугольника.
В + Г/2 – 1,
где В есть количество целочисленных точек внутри многоугольника, а Г количество целочисленных точек на границе многоугольника.
Слайд 8Доказательство теоремы Пика.
Любой такой многоугольник легко разбить на треугольники
с вершинами в узлах решётки, не содержащие узлов ни внутри, ни на сторонах. Можно показать, что площади всех этих треугольников одинаковы и равны 1/2, а, следовательно, площадь многоугольника равна половине их числа Т.
Чтобы найти это число, обозначим через п число сторон многоугольника, через i — число узлов внутри его и через b — число узлов на сторонах, включая вершины. Общая сумма углов всех треугольников равна πТ. Теперь найдём эту сумму другим способом.
Сумма углов с вершиной в любом внутреннем узле составляет 2π, т. е. общая сумма таких углов равна 2πi; общая сумма углов при узлах на сторонах, но не в вершинах равна (b – n) π, а сумма углов при вершинах многоугольника — (п – 2) π. Таким образом, πТ = 2iπ + (b – n) π + (n – 2) π, откуда получаем выражение для площади S многоугольника, известное как формула Пика.
Например, на рисунке b = 9, i = 24, а следовательно, площадь многоугольника равна 27,5.
Чтобы найти это число, обозначим через п число сторон многоугольника, через i — число узлов внутри его и через b — число узлов на сторонах, включая вершины. Общая сумма углов всех треугольников равна πТ. Теперь найдём эту сумму другим способом.
Сумма углов с вершиной в любом внутреннем узле составляет 2π, т. е. общая сумма таких углов равна 2πi; общая сумма углов при узлах на сторонах, но не в вершинах равна (b – n) π, а сумма углов при вершинах многоугольника — (п – 2) π. Таким образом, πТ = 2iπ + (b – n) π + (n – 2) π, откуда получаем выражение для площади S многоугольника, известное как формула Пика.
Например, на рисунке b = 9, i = 24, а следовательно, площадь многоугольника равна 27,5.
Слайд 9Применение.
Итак, вернемся к заданию В6. Теперь, зная новую формулы, мы легко
сможем найти площадь этого четырехугольника.
Так как В – 5; Г – 14, то 5+14:2-1=11 (см в квадрате)
Площадь данного четырехугольника равна 11 см в квадрате.
Так как В – 5; Г – 14, то 5+14:2-1=11 (см в квадрате)
Площадь данного четырехугольника равна 11 см в квадрате.
Слайд 10 По той же формуле мы можем найти площадь треугольника.
Так как В-14,
Г-10,то 14+10:2-1=18 (см в квадрате)
Площадь данного треугольника равна 18 см в квадрате.
Площадь данного треугольника равна 18 см в квадрате.
Слайд 11 Если В-9, Г-12, тогда: 9+12:2-1=14 (см в квадрате)
Площадь данного четырехугольника равна
14 см в квадрате.
Слайд 12Области применения формулы.
Помимо того, что формула применяется в различного рода экзаменах,
заданиях и так далее, она сопровождает весь окружающий нас мир.
Слайд 13По формуле Пика S =В +½Г-1
1)туловище В=9,Г=26, S=9+½·26-1=9+13-1=21
2)хвост В=0,Г=8, S=0+½·8-1=3
3) S=21+3=24
Слайд 15Заключение.
В итоге, я пришла к выводу, что существует много различных способов
решения задач на нахождение площади, не изучаемых в школьной программе, и показала их на примере формулы Пика.
Слайд 16Справочник.
Многоугольник без самопересечений называется решётчатым, если все его вершины находятся в
точках с целочисленными координатами (в декартовой системе координат).
Точка координатной плоскости называется целочисленной, если обе её координаты целые.
Точка координатной плоскости называется целочисленной, если обе её координаты целые.