- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Золотое сечение
Содержание
- 1. Презентация по математике Золотое сечение
- 2. Введение.Человек различает окружающие его предметы по форме.
- 3. Цель.Воспользовавшись различной литературой по геометрии, по черчению,
- 4. Задачи.Ввести понятие «Золотого сечение» (немного об истории).Рассмотреть
- 5. Принято считать, что понятие о золотом делении
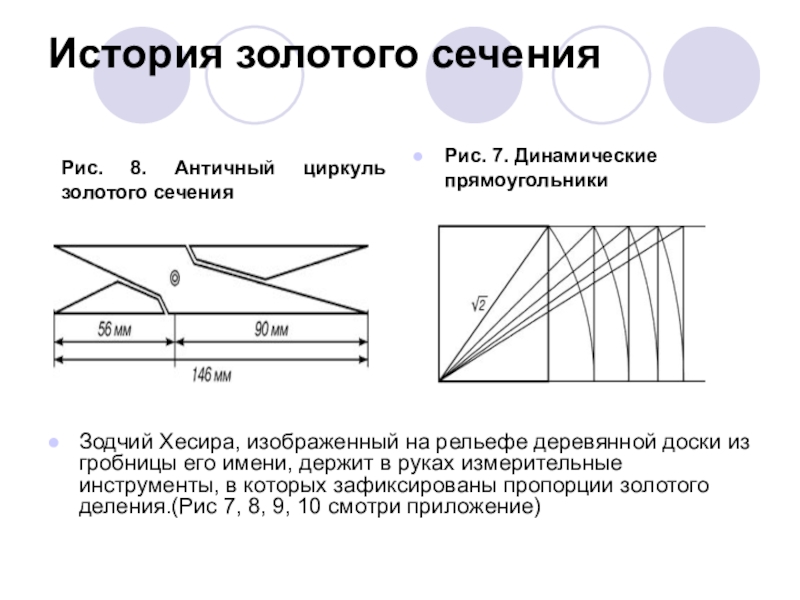
- 6. История золотого сеченияРис. 7. Динамические прямоугольникиЗодчий Хесира,
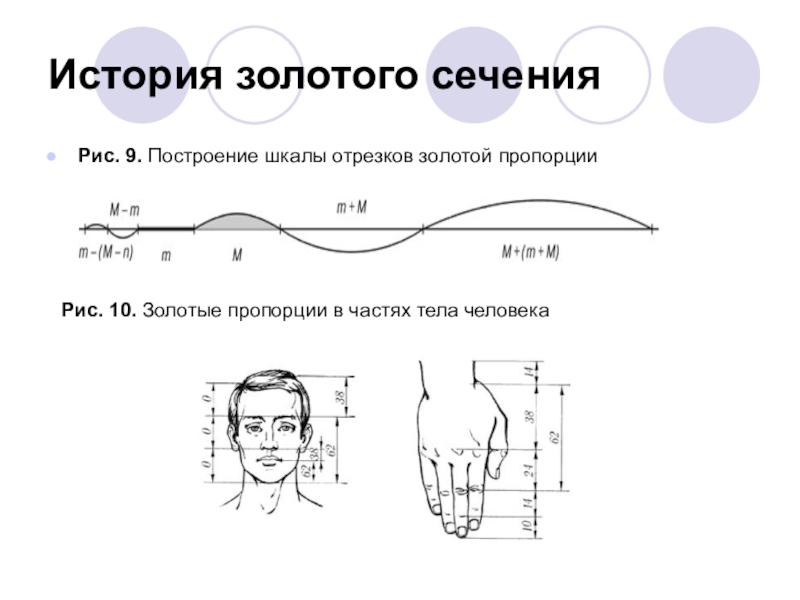
- 7. История золотого сеченияРис. 9. Построение шкалы отрезков золотой пропорцииРис. 10. Золотые пропорции в частях тела человека
- 8. Золотое сечение – гармоническая пропорция В математике
- 9. Золотое сечение – гармоническая пропорцияПрактическое знакомство с
- 10. Золотое сечение – гармоническая пропорцияРис. 3. Построение
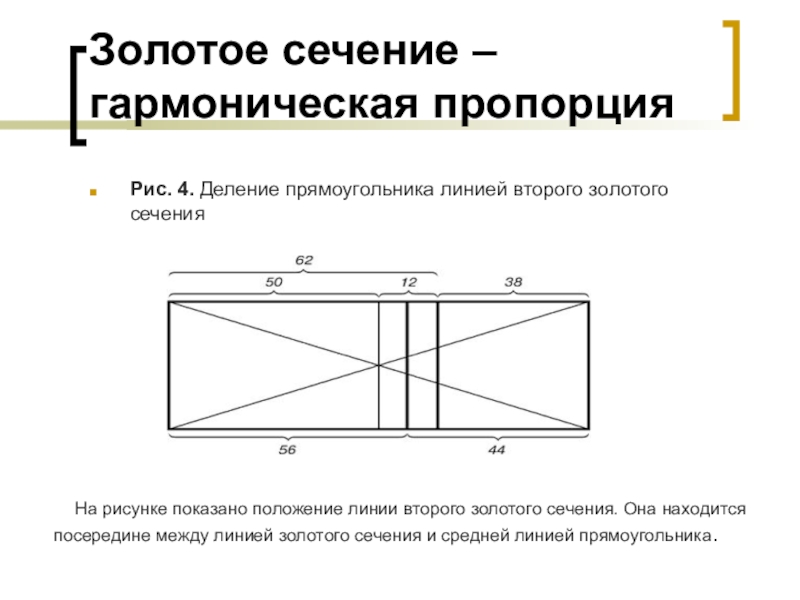
- 11. Золотое сечение – гармоническая пропорцияРис. 4. Деление
- 12. Обобщенное золотое сечениеУченые продолжали активно развивать теорию
- 13. Ряд ФибоначчиРяд чисел 0, 1, 1, 2,
- 14. Принципы формообразования в природеВсе, что приобретало
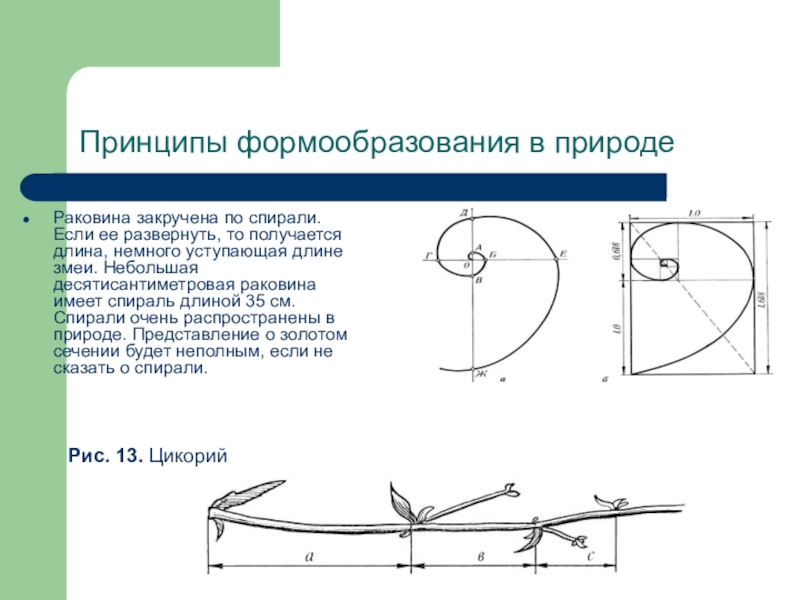
- 15. Принципы формообразования в природеРаковина закручена по спирали.
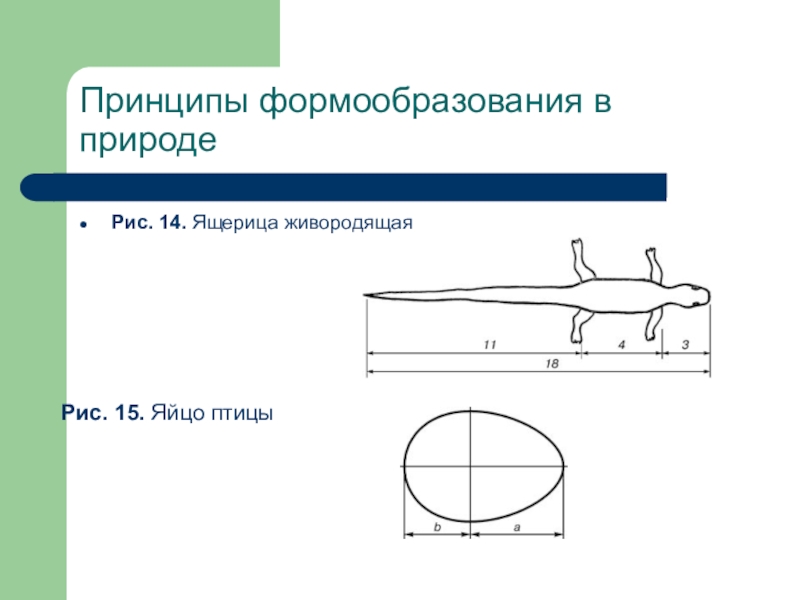
- 16. Принципы формообразования в природеРис. 14. Ящерица живородящаяРис. 15. Яйцо птицы
- 17. Золотое сечение и симметрия.Золотое сечение нельзя рассматривать
- 18. Золотое сечение в архитектуре.Многие исследователи, стремившиеся раскрыть
- 19. Золотое сечение в архитектуре.Это древнее сооружение с
- 20. Золотое сечение в архитектуре. Храм Василия Блаженного.В этом
- 21. Здание бывшего Сената в Москве.дом Пашкова.
- 22. Заключение.Я думаю, что мой реферат можно использовать
- 23. Спасибо за внимание!
Слайд 2Введение.
Человек различает окружающие его предметы по форме. Интерес к форме какого-либо
Слайд 3Цель.
Воспользовавшись различной литературой по геометрии, по черчению, различными справочными материалами для
Слайд 4Задачи.
Ввести понятие «Золотого сечение» (немного об истории).
Рассмотреть применение «Золотого сечение» в
Рассмотрим золотую пропорцию и связанные с нею отношения.
Продемонстрировать и разобрать понятие золотой спирали в живой природе.
Рассмотреть использование золотого сечения в архитектуре.
Слайд 5Принято считать, что понятие о золотом делении ввел в научный обиход
История золотого сечения
Слайд 6История золотого сечения
Рис. 7. Динамические прямоугольники
Зодчий Хесира, изображенный на рельефе деревянной
Рис. 8. Античный циркуль золотого сечения
Слайд 7История золотого сечения
Рис. 9. Построение шкалы отрезков золотой пропорции
Рис. 10. Золотые
Слайд 8Золотое сечение – гармоническая пропорция
В математике пропорцией (лат. proportio) называют
Отрезок прямой АВ можно разделить на две части следующими способами:
на две равные части – АВ : АС = АВ : ВС;
на две неравные части в любом отношении (такие части пропорции не образуют);
таким образом, когда АВ : АС = АС : ВС.
Последнее и есть золотое деление или деление отрезка в крайнем и среднем отношении.
Золотое сечение – это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей; или другими словами, меньший отрезок так относится к большему, как больший ко всему
a : b = b : c или с : b = b : а.
Рис. 1. Геометрическое изображение золотой пропорции
Слайд 9Золотое сечение – гармоническая пропорция
Практическое знакомство с золотым сечением начинают с
Рис. 2. Деление отрезка прямой по золотому сечению. BC = 1/2 AB; CD = BC
Из точки В восставляется перпендикуляр, равный половине АВ. Полученная точка С соединяется линией с точкой А. На полученной линии откладывается отрезок ВС, заканчивающийся точкой D. Отрезок AD переносится на прямую АВ. Полученная при этом точка Е делит отрезок АВ в соотношении золотой пропорции.
Слайд 10Золотое сечение – гармоническая пропорция
Рис. 3. Построение второго золотого сечения
Деление осуществляется
Слайд 11Золотое сечение – гармоническая пропорция
Рис. 4. Деление прямоугольника линией второго золотого
На рисунке показано положение линии второго золотого сечения. Она находится посередине между линией золотого сечения и средней линией прямоугольника.
Слайд 12Обобщенное золотое сечение
Ученые продолжали активно развивать теорию чисел Фибоначчи и золотого
Слайд 13Ряд Фибоначчи
Ряд чисел 0, 1, 1, 2, 3, 5, 8, 13,
Фибоначчи так же занимался решением практических нужд торговли: с помощью какого наименьшего количества гирь можно взвесить товар? Фибоначчи доказывает, что оптимальной является такая система гирь: 1, 2, 4, 8, 16...
Слайд 14Принципы формообразования
в природе
Все, что приобретало какую-то форму, образовывалось, росло, стремилось
Слайд 15Принципы формообразования в природе
Раковина закручена по спирали. Если ее развернуть, то
Рис. 13. Цикорий
Слайд 17Золотое сечение и симметрия.
Золотое сечение нельзя рассматривать само по себе, отдельно,
Золотое деление не есть проявление асимметрии, чего-то противоположного симметрии Согласно современным представлениям золотое деление – это асимметричная симметрия. В науку о симметрии вошли такие понятия, как статическая и динамическая симметрия. Статическая симметрия характеризует покой, равновесие, а динамическая – движение, рост. Так, в природе статическая симметрия представлена строением кристаллов, а в искусстве характеризует покой, равновесие и неподвижность. Динамическая симметрия выражает активность, характеризует движение, развитие, ритм, она – свидетельство жизни. Статической симметрии свойственны равные отрезки, равные величины. Динамической симметрии свойственно увеличение отрезков или их уменьшение, и оно выражается в величинах золотого сечения возрастающего или убывающего ряда.
Слайд 18Золотое сечение в архитектуре.
Многие исследователи, стремившиеся раскрыть секрет гармонии Парфенона, искали
Рис. Золотое сечение в пропорциях Парфенона
Слайд 19Золотое сечение в архитектуре.
Это древнее сооружение с его гармоническими пропорциями дарит
На рисунке виден целый ряд закономерностей, связанных с коэффициентом золотого сечения.
Знаменитый русский архитектор М.Ф.Казаков широко использовал в своем творчестве золотое сечение. Его талант был многогранным, но в большей степени он проявился в многочисленных проектах жилых домов и усадеб. Например, золотое сечение можно встретить в архитектуре здания бывшего сената в Кремле (см. Приложение, рис. 2), Дворца в Петровском Алабине и Голицынской больницы в Москве, которая в настоящее время называется. Первой Клинической больницей имени Н.И.Пирогова.
Слайд 20Золотое сечение в архитектуре.
Храм Василия Блаженного.
В этом членении и заключена основная
Слайд 22Заключение.
Я думаю, что мой реферат можно использовать для изучения «золотого сечения».
В реферате затронуты все опорно - полагающие аспекты.
Рассмотрено применение «золотого сечения» в искусстве с древних времен до наших дней.
Описано применение «золотого сечения» в архитектуре.