г.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Виды правильных многогранников
Содержание
- 1. Презентация по математике Виды правильных многогранников
- 2. Цель: познакомиться с видами правильных многогранников.Задачи: дать
- 3. Определение Правильный многогранник или платоново тело -
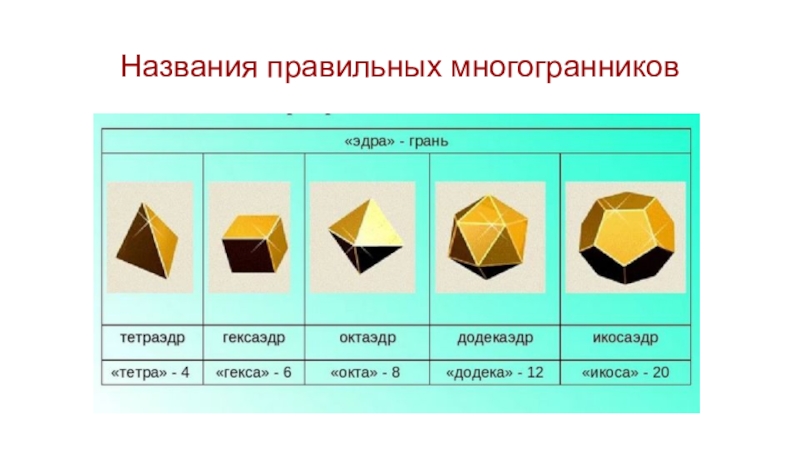
- 4. Названия правильных многогранников
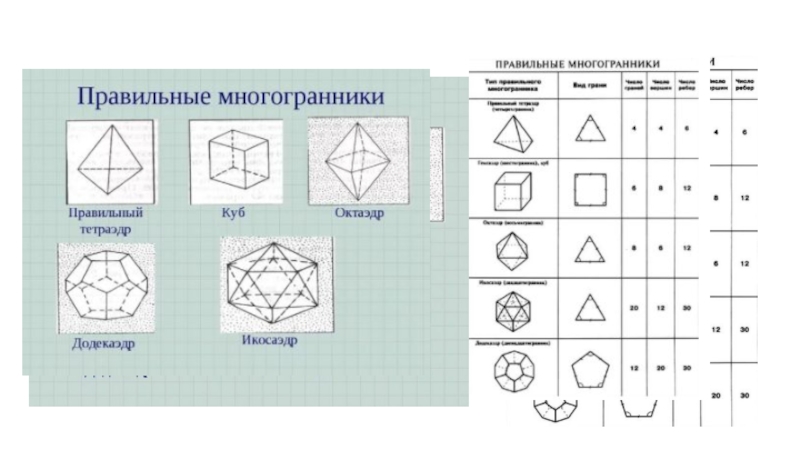
- 5. Слайд 5
- 6. ИсторияПравильные многогранники известны с древнейших времён. Их
- 7. ИсторияПравильные многогранники характерны для философии Платона, в
- 8. ИсторияЕвклид дал полное математическое описание правильных многогранников
- 9. Комбинаторные свойстваЭйлером была выведена формула, связывающая число
- 10. Комбинаторные свойстваОтношение количества вершин правильного многогранника к
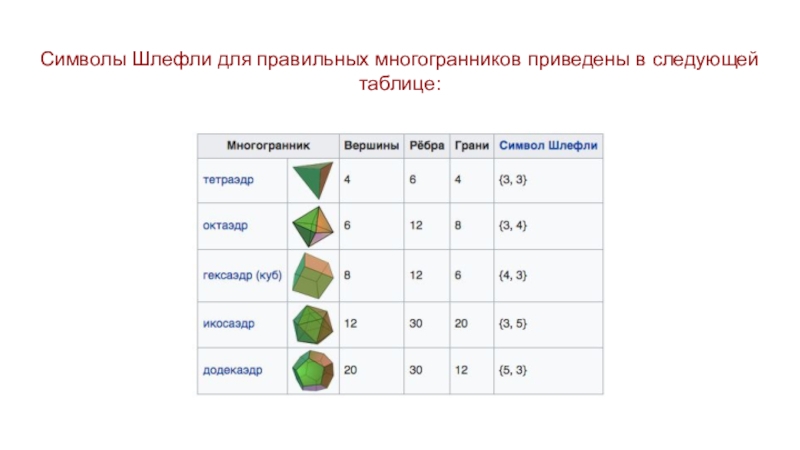
- 11. Символы Шлефли для правильных многогранников приведены в следующей таблице:
- 12. Выводы:В результате работы:узнали историю изучения правильных многогранников
- 13. Источники информации:https://ru.wikipedia.org/wiki/%D0%9F%D1%80%D0%B0%D0%B2%D0%B8%D0%BB%D1%8C%D0%BD%D1%8B%D0%B9_%D0%BC%D0%BD%D0%BE%D0%B3%D0%BE%D0%B3%D1%80%D0%B0%D0%BD%D0%BD%D0%B8%D0%BAhttps://ru.wikipedia.org/wiki/%D0%9F%D0%BB%D0%B0%D1%82%D0%BE%D0%BDhttps://ru.wikipedia.org/wiki/%D0%95%D0%B2%D0%BA%D0%BB%D0%B8%D0%B4https://yandex.ru/search/?clid=2186620&text=%D1%8D%D0%B9%D0%BB%D0%B5%D1%80%20%D0%BB%D0%B5%D0%BE%D0%BD%D0%B0%D1%80%D0%B4&lr=54&redircnt=1522047434.1https://ru.wikipedia.org/wiki/%D0%A8%D0%BB%D0%B5%D1%84%D0%BB%D0%B8,_%D0%9B%D1%8E%D0%B4%D0%B2%D0%B8%D0%B3https://yandex.ru/images/search?p=1&text=%D0%9F%D1%80%D0%B0%D0%B2%D0%B8%D0%BB%D1%8C%D0%BD%D1%8B%D0%B5%20%D0%BC%D0%BD%D0%BE%D0%B3%D0%BE%D0%B3%D1%80%D0%B0%D0%BD%D0%BD%D0%B8%D0%BA%D0%B8&img_url=https%3A%2F%2Fcf.ppt-online.org%2Ffiles%2Fslide%2Fw%2Fw6VGqBrouMR2WPzcHpNf4dTaj9s50yAkYhFZ8X%2Fslide-2.jpg&pos=40&rpt=simage
Цель: познакомиться с видами правильных многогранников.Задачи: дать основную информацию о правильных многогранниках;разобрать названия правильных многогранников;познакомить с историей изучения правильных многогранников.
Слайд 1Виды правильных многогранников
ГБУ СО ЦППМСП “Ресурс”
педагог дополнительного образования Задумина Т.М.
Екатеринбург, 2019
Слайд 2Цель: познакомиться с видами правильных многогранников.
Задачи:
дать основную информацию о правильных
многогранниках;
разобрать названия правильных многогранников;
познакомить с историей изучения правильных многогранников.
разобрать названия правильных многогранников;
познакомить с историей изучения правильных многогранников.
Слайд 3Определение
Правильный многогранник или платоново тело - это выпуклый многогранник, состоящий
из одинаковых правильных многоугольников и обладающий пространственной симметрией.
Многогранник называется правильным если:
он выпуклый;
все его грани являются равными правильными
многоугольниками;
в каждой его вершине сходится одинаковое
число рёбер.
Многогранник называется правильным если:
он выпуклый;
все его грани являются равными правильными
многоугольниками;
в каждой его вершине сходится одинаковое
число рёбер.
Слайд 6История
Правильные многогранники известны с древнейших времён. Их орнаментные модели можно найти
на резных каменных шарах, созданных в период позднего неолита, в Шотландии, как минимум за 1000 лет до Платона. В костях, которыми люди играли на заре цивилизации, уже угадываются формы правильных многогранников.
В значительной мере правильные многогранники были изучены древними греками. Некоторые источники (такие как Прокл Диадох) приписывают честь их открытия Пифагору. Другие утверждают, что ему были знакомы только тетраэдр, куб и додекаэдр, а честь открытия октаэдра и икосаэдра принадлежит Теэтету Афинскому, современнику Платона. В любом случае, Теэтет дал математическое описание всем пяти правильным многогранникам и первое известное доказательство того, что их ровно пять.
В значительной мере правильные многогранники были изучены древними греками. Некоторые источники (такие как Прокл Диадох) приписывают честь их открытия Пифагору. Другие утверждают, что ему были знакомы только тетраэдр, куб и додекаэдр, а честь открытия октаэдра и икосаэдра принадлежит Теэтету Афинскому, современнику Платона. В любом случае, Теэтет дал математическое описание всем пяти правильным многогранникам и первое известное доказательство того, что их ровно пять.
Слайд 7История
Правильные многогранники характерны для философии Платона, в честь которого и получили
название «платоновы тела». Платон писал о них в своём трактате Тимей (360г до н. э.), где сопоставил каждую из четырёх стихий (землю, воздух, воду и огонь) определённому правильному многограннику.
Земля сопоставлялась кубу,
воздух — октаэдру,
вода — икосаэдру,
огонь — тетраэдру.
Плато́н (др.-греч. Πλάτων, между 429 и 427 до н. э., Афины — 347 до н. э., там же) — древнегреческий философ, ученик Сократа, учитель Аристотеля
Земля сопоставлялась кубу,
воздух — октаэдру,
вода — икосаэдру,
огонь — тетраэдру.
Плато́н (др.-греч. Πλάτων, между 429 и 427 до н. э., Афины — 347 до н. э., там же) — древнегреческий философ, ученик Сократа, учитель Аристотеля
Слайд 8История
Евклид дал полное математическое описание правильных многогранников в последней, XIII книге
Начал. Предложения 13—17 этой книги описывают структуру тетраэдра, октаэдра, куба, икосаэдра и додекаэдра в данном порядке.
Для каждого многогранника Евклид нашёл отношение диаметра описанной сферы к длине ребра. В 18-м предложении утверждается, что не существует других правильных многогранников.
Евкли́д или Эвкли́д (др.-греч. Εὐκλείδης, от «добрая слава», время расцвета — около 300 года до н. э.) — древнегреческий математик, автор первого из дошедших до нас теоретических трактатов по математике.
Для каждого многогранника Евклид нашёл отношение диаметра описанной сферы к длине ребра. В 18-м предложении утверждается, что не существует других правильных многогранников.
Евкли́д или Эвкли́д (др.-греч. Εὐκλείδης, от «добрая слава», время расцвета — около 300 года до н. э.) — древнегреческий математик, автор первого из дошедших до нас теоретических трактатов по математике.
Слайд 9Комбинаторные свойства
Эйлером была выведена формула, связывающая число вершин (В), граней (Г)
и рёбер (Р) любого выпуклого многогранника простым соотношением:
В + Г = Р + 2.
Леона́рд Э́йлер (нем. Leonhard Euler; 15 апреля 1707, Базель, Швейцария — 7 (18) сентября 1783, Санкт-Петербург, Российская империя).
Швейцарский, немецкий и российский математик и механик, внёсший фундаментальный вклад в развитие этих наук. Эйлер - автор более чем 850 работ по математическому анализу, дифференциальной геометрии, теории чисел, приближённым вычислениям, небесной механике, математической физике, оптике, баллистике, кораблестроению, теории музыки и другим областям.
В + Г = Р + 2.
Леона́рд Э́йлер (нем. Leonhard Euler; 15 апреля 1707, Базель, Швейцария — 7 (18) сентября 1783, Санкт-Петербург, Российская империя).
Швейцарский, немецкий и российский математик и механик, внёсший фундаментальный вклад в развитие этих наук. Эйлер - автор более чем 850 работ по математическому анализу, дифференциальной геометрии, теории чисел, приближённым вычислениям, небесной механике, математической физике, оптике, баллистике, кораблестроению, теории музыки и другим областям.
Слайд 10Комбинаторные свойства
Отношение количества вершин правильного многогранника к количеству рёбер одной его
грани равно отношению количества граней этого же многогранника к количеству рёбер, выходящих из одной его вершины. У тетраэдра это отношение равно 4:3, у гексаэдра и октаэдра — 2:1, а у додекаэдра и икосаэдра — 4:1.
Правильный многогранник может быть комбинаторно описан символом Шлефли {p, q}, где:
p — число рёбер в каждой грани;
q — число рёбер, сходящихся в каждой вершине
.
Людвиг Шлефли (нем. Ludwig Schläfli; 15 января 1814, Грасвиль, нынешний Зеберг — 20 марта 1895, Берн) — швейцарский математик, специалист в области многомерной геометрии и комплексного анализа.
Правильный многогранник может быть комбинаторно описан символом Шлефли {p, q}, где:
p — число рёбер в каждой грани;
q — число рёбер, сходящихся в каждой вершине
.
Людвиг Шлефли (нем. Ludwig Schläfli; 15 января 1814, Грасвиль, нынешний Зеберг — 20 марта 1895, Берн) — швейцарский математик, специалист в области многомерной геометрии и комплексного анализа.
Слайд 12Выводы:
В результате работы:
узнали историю изучения правильных многогранников и их названий;
рассмотрели происхождение
названий и некоторые свойства правильных многогранников;
познакомились с жизнедеятельностью ученых-математиков.
познакомились с жизнедеятельностью ученых-математиков.