Ксении Семеновны Константиновой»
Преподаватель дисциплины "Математика" Абреимова Анна Александровна
2017 г.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Цилиндр
Содержание
- 1. Презентация по математике Цилиндр
- 2. ЦЕЛИ:
- 3. ОСНОВНЫЕ ВОПРОСЫ
- 4. ИЗ ИСТОРИИ ТЕРМИНОЛОГИИЦилиндр – в переводе с греческого «валик», «каток», «вращаю».
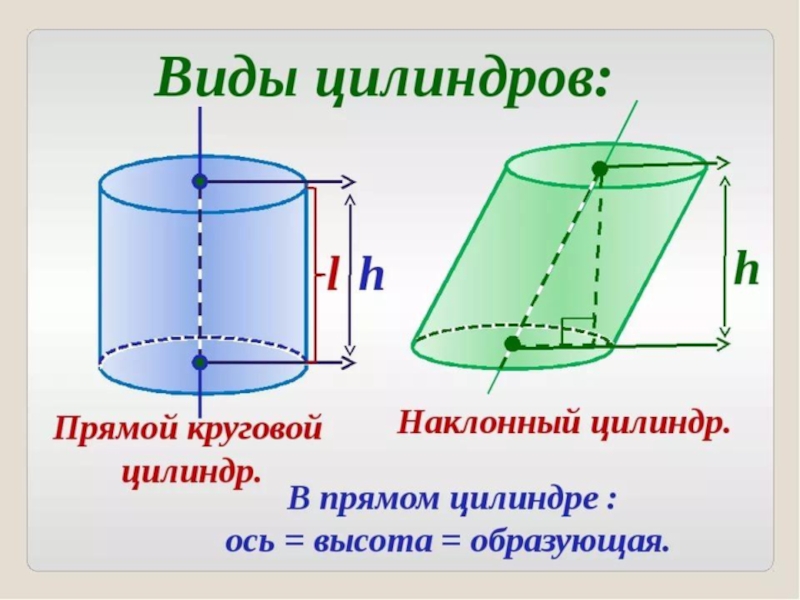
- 5. Цилиндром называется тело вращения, полученное при вращении
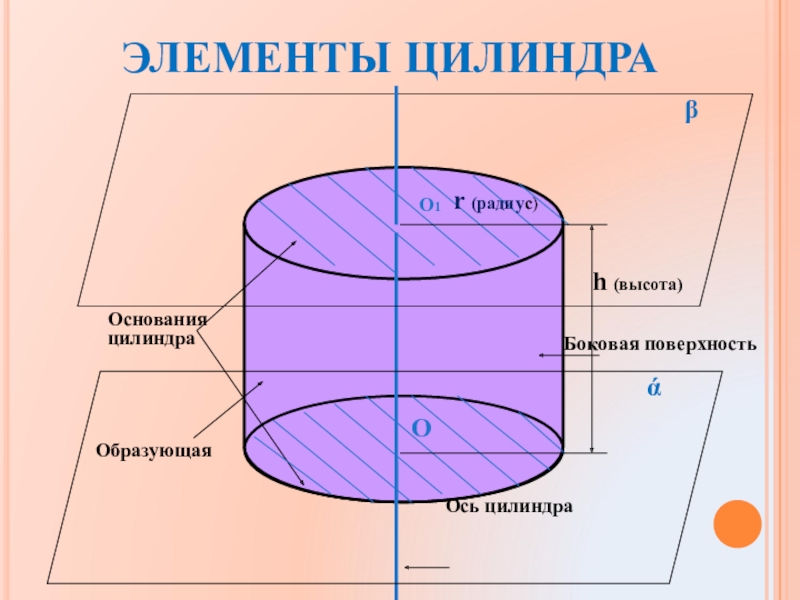
- 6. ОснованияцилиндраБоковая поверхностьОсь цилиндраОбразующаяЭЛЕМЕНТЫ ЦИЛИНДРА
- 7. Отрезки, соединяющие окружности оснований и перпендикулярные их
- 8. Перпендикуляр, опущенный из любой плоскости одного основания
- 9. Слайд 9
- 10. Если секущая плоскость проходит через ось цилиндра, то сечение представляет собой прямоугольник и называется осевымСЕЧЕНИЯ ЦИЛИНДРА
- 11. СЕЧЕНИЯ ЦИЛИНДРАЕсли секущая плоскость перпендикулярна к оси цилиндра, то сечение является кругом.
- 12. СЕЧЕНИЯ ЦИЛИНДРАЕсли секущая плоскость не перпендикулярна к
- 13. СЕЧЕНИЯ ЦИЛИНДРАПлоскость сечения параллельна оси цилиндра и перпендикулярна основаниям. В сечении – прямоугольник
- 14. Свойства цилиндраСвойство 1: Все образующие цилиндра равны
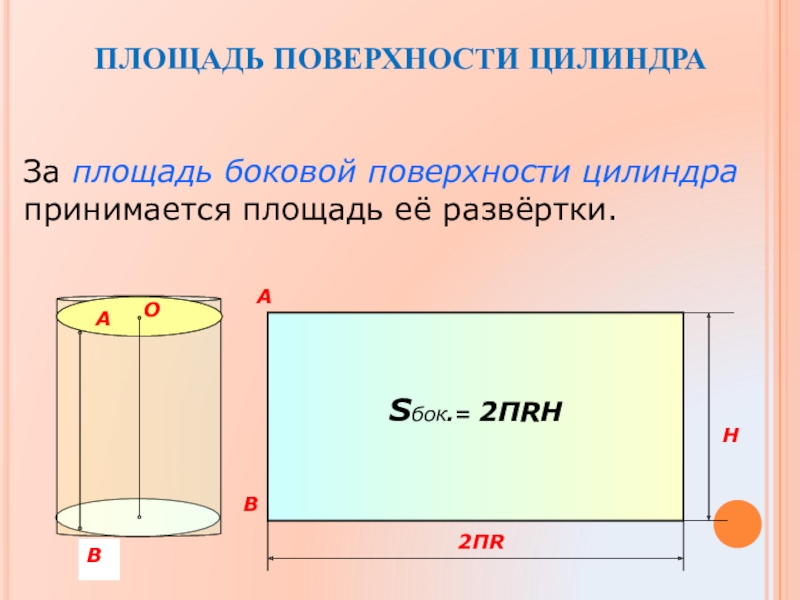
- 15. ПЛОЩАДЬ ПОВЕРХНОСТИ ЦИЛИНДРАЗа площадь боковой поверхности цилиндра принимается площадь её развёртки.OABSбок.= 2ПRH2ПRH
- 16. ПЛОЩАДЬ ПОВЕРХНОСТИ ЦИЛИНДРАПлощадь боковой поверхности цилиндра равна
- 17. ПРИМЕРЫ ЦИЛИНДРА В МЕДИЦИНЕ
- 18. Практические задания.
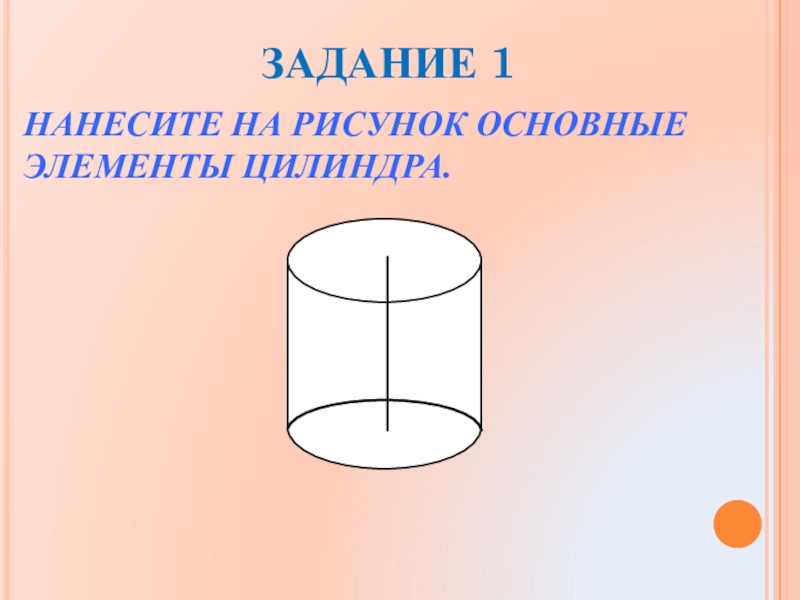
- 19. НАНЕСИТЕ НА РИСУНОК ОСНОВНЫЕ ЭЛЕМЕНТЫ ЦИЛИНДРА. ЗАДАНИЕ 1
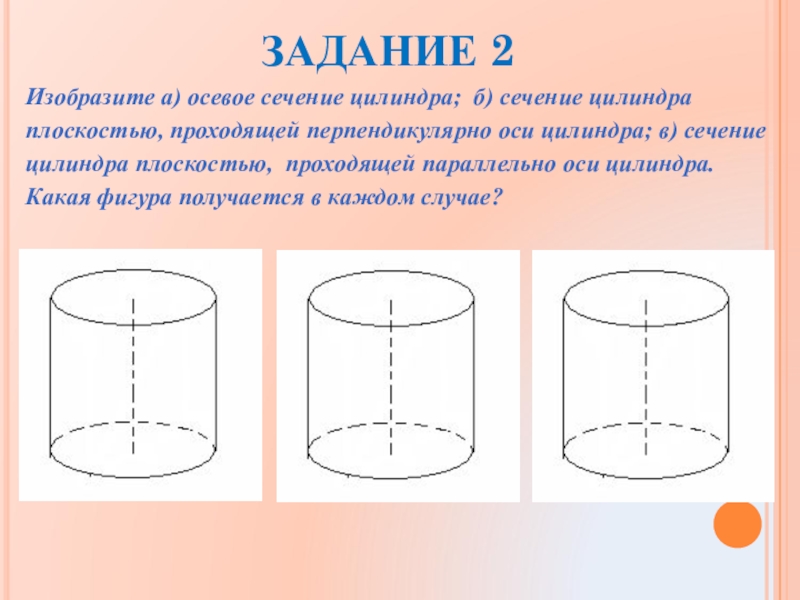
- 20. Изобразите а) осевое сечение цилиндра; б) сечение
- 21. Во сколько раз увеличится боковая поверхность цилиндра,
- 22. НАЙДИТЕ ПЛОЩАДЬ ЛИСТА ЖЕСТИ, ЕСЛИ ИЗ НЕГО
- 23. ЗАДАНИЕ 5Осевое сечение цилиндра – квадрат, диагональ
- 24. РЕШЕНИЕ:А)Б)Дано:ЦилиндрВД = 20смАВСД – осевое сечение, квадрат.
- 25. ДОМАШНЕЕ ЗАДАНИЕ.1. Теория:Учебник:Математика : учеб.
- 26. 2. Практика:Сборник задач по математике: учеб. Пособие
- 27. Слайд 27
ЦЕЛИ:
Слайд 5Цилиндром называется тело вращения, полученное при вращении прямоугольника вокруг оси, проходящей
через одну из его сторон.
ОПРЕДЕЛЕНИЕ ЦИЛИНДРА
Слайд 7Отрезки, соединяющие окружности оснований и перпендикулярные их плоскости, называются – образующими
цилиндра.
Отрезок, соединяющий центры оснований, называется – осью цилиндра.
ЭЛЕМЕНТЫ ЦИЛИНДРА
В основаниях – два равных круга
Слайд 8Перпендикуляр, опущенный из любой плоскости одного основания цилиндра на плоскость другого
его основания, называется высотой цилиндра (иначе длина образующей). Т.к. плоскости оснований параллельны, то перпендикуляры у них общие и все они равны. Поэтому высоту можно проводить из любой точки плоскости основания.
ЭЛЕМЕНТЫ ЦИЛИНДРА
Слайд 10Если секущая плоскость проходит через ось цилиндра, то сечение представляет собой
прямоугольник и называется осевым
СЕЧЕНИЯ ЦИЛИНДРА
Слайд 11СЕЧЕНИЯ ЦИЛИНДРА
Если секущая плоскость перпендикулярна к оси цилиндра, то сечение является
кругом.
Слайд 12СЕЧЕНИЯ ЦИЛИНДРА
Если секущая плоскость не перпендикулярна к оси цилиндра и имеет
не более одной общей точки с каждым из оснований, то сечение является эллипсом
Слайд 13СЕЧЕНИЯ ЦИЛИНДРА
Плоскость сечения параллельна оси цилиндра и перпендикулярна основаниям. В сечении
– прямоугольник
Слайд 14Свойства цилиндра
Свойство 1: Все образующие цилиндра равны друг другу.
Свойство 2: Основания
цилиндра равны друг другу.
Свойство 3: Все сечения цилиндра плоскостями, параллельными плоскостям основания цилиндра, равны основаниям цилиндра.
Свойство 3: Все сечения цилиндра плоскостями, параллельными плоскостям основания цилиндра, равны основаниям цилиндра.
Слайд 15ПЛОЩАДЬ ПОВЕРХНОСТИ ЦИЛИНДРА
За площадь боковой поверхности цилиндра принимается площадь её развёртки.
O
A
B
Sбок.=
2ПRH
2ПR
H
Слайд 16ПЛОЩАДЬ ПОВЕРХНОСТИ ЦИЛИНДРА
Площадь боковой поверхности цилиндра равна произведению длины окружности основания
на высоту цилиндра.
Площадью полной поверхности цилиндра является сумма площадей боковой поверхности и двух оснований
Sполн. = Sбок. + 2Sосн.
(Sбок.= 2ПRH)
(Sосн. = ПR²)
O
Sполн = 2πR(R + h)
Слайд 20Изобразите а) осевое сечение цилиндра; б) сечение цилиндра плоскостью, проходящей перпендикулярно
оси цилиндра; в) сечение цилиндра плоскостью, проходящей параллельно оси цилиндра. Какая фигура получается в каждом случае?
ЗАДАНИЕ 2
Слайд 21Во сколько раз увеличится боковая поверхность цилиндра, если его высота увеличится
в 5 раз, а радиус основания останется прежним?
Ответ: площадь боковой поверхности увеличится в 5 раз.
Sбок =2πRh
R
5h
R
h
Sбок =2πR5h = 10πRh
ЗАДАНИЕ 3
Слайд 22НАЙДИТЕ ПЛОЩАДЬ ЛИСТА ЖЕСТИ, ЕСЛИ ИЗ НЕГО ИЗГОТОВЛЕНА ТРУБА ДЛИНОЙ 8
м И ДИАМЕТРОМ 32 см?
Дано:
цилиндр
h = 8 м, d = 32 см.
Найти: Sбок
8 м
32 см
S - ?
ЗАДАНИЕ 4
ОТВЕТ: Sбок = 80384 см2 = 803, 84 м2
Слайд 23ЗАДАНИЕ 5
Осевое сечение цилиндра – квадрат, диагональ которого равна 20 см.
Найти:
а) высоту цилиндра;
б) площадь основания цилиндра.
Слайд 24РЕШЕНИЕ:
А)
Б)
Дано:
Цилиндр
ВД = 20см
АВСД – осевое сечение, квадрат.
Найти:
h - ?;
Решение:
а) Так как АВСД – квадрат, то
АВ=АД.
Из треугольника АВД по теореме Пифагора: АС2 = ВА2 + АД;
202 = h2 + h2;
202 = 2h2;
400 = 2 h2;
h2 = 200;
h = 10√2.
Дано:
цилиндр
АВСД – осевое сечение, квадрат.
Найти:
Sосн - ?
Решение:
б) Sосн = πr2; r = 1/2АД; r =1/2h;
R = (1*10√2)/2= 5√5 ; Sосн = π(3√2 )2;
Sосн = π ·25(√2 )2;
Sосн = π50.
ВД = 20см
Слайд 25
ДОМАШНЕЕ ЗАДАНИЕ.
1. Теория:Учебник:
Математика : учеб. для ссузов / Н.В. Богомолов,
П.И. Самойленко. – 5 – е изд., стереотип. – М. : Дрофа, 2008. – 395, [5] с. : ил.
Глава I4. §86. Пункты 1-2, стр. 344 - 346.
2. Практика:
Сборник задач по математике:
учеб. Пособие для ссузов/ Н.В. Богомолов. – 8 – е изд., стереотип. – М.: Дрофа, 2012, - 204, [4]с.: ил.
Глава 8. Элементы стереометрии.
§ 54. № 508, стр. 86.
Глава I4. §86. Пункты 1-2, стр. 344 - 346.
2. Практика:
Сборник задач по математике:
учеб. Пособие для ссузов/ Н.В. Богомолов. – 8 – е изд., стереотип. – М.: Дрофа, 2012, - 204, [4]с.: ил.
Глава 8. Элементы стереометрии.
§ 54. № 508, стр. 86.
Слайд 262. Практика:
Сборник задач по математике:
учеб. Пособие для ссузов/ Н.В. Богомолов.
– 8 – е изд., стереотип. – М.: Дрофа, 2012, - 204, [4]с.: ил.
Глава 8. Элементы стереометрии.
§ 54. № 508
Диагональ осевого сечения цилиндра а = 26 см, а высота h = 24 см. Вычислите площадь основания цилиндра.
Глава 8. Элементы стереометрии.
§ 54. № 508
Диагональ осевого сечения цилиндра а = 26 см, а высота h = 24 см. Вычислите площадь основания цилиндра.
