- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Теорема Пифагора
Содержание
- 1. Презентация по математике Теорема Пифагора
- 2. 20 в. до н.э.6 в. до н.э.Дано:
- 3. Рафаэль. Пифагор в окружении учеников
- 4. 6 в. до н.э.Дано: треугольник –прямоугольныйДоказать: с2 = а2 + в2
- 5. 20 в. до н.э.Дано: с2 = а2 + в2Доказать: треугольник –прямоугольный
- 6. 1234Номер прямоугольного треугольника + доказательство41 = 25 + 1613 = 4 + 9
- 7. Слайд 7
- 8. 1940 год Э. Лумис «Пифагорово предложение»367 доказательств.Евклид. «Начала.» 1482г.
- 9. Задача Леонарда Пизанского, XIII век.Две башни
- 10. Задача Леонарда Пизанского, XIII век.CB=22,5BD=37,550 + x = (60-x) + 402222
- 11. Задача древнекитайского ученого Цзинь Киу -
- 12. Слайд 12
- 13. Слайд 13
- 14. Слайд 14
- 15. Слайд 15
- 16. Слайд 16
- 17. Слайд 17
- 18. Слайд 18
- 19. Заполни таблицу
- 20. Слайд 20
- 21. Про теорему Пифагора и не только о ней...
20 в. до н.э.6 в. до н.э.Дано: с2 = а2 + в2Доказать: треугольник –прямоугольныйДано: треугольник –прямоугольныйДоказать: с2 = а2 + в2
Слайд 1Теорема Пифагора
Прямая теорема
Обратная теорема
Задача Фибоначчи
Задача Цзинь Киу-чау
ОГЭ
Рафаэль
Задача
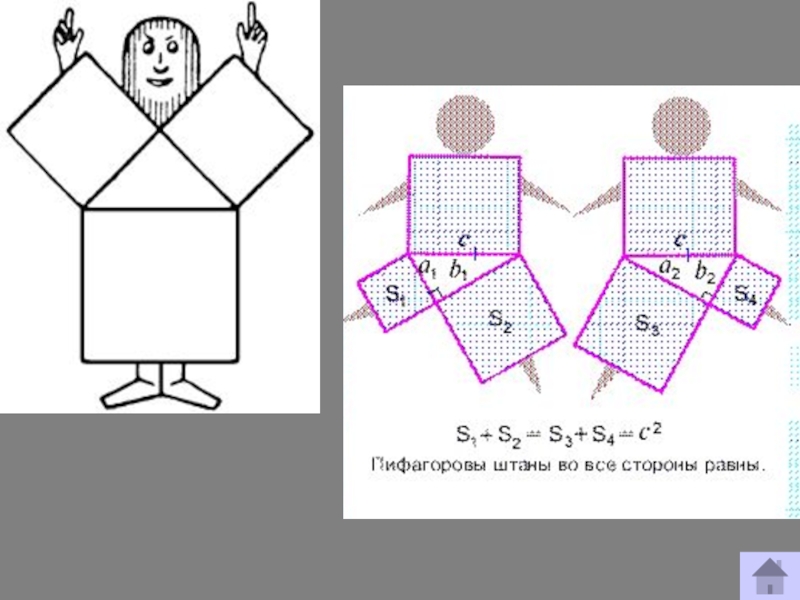
Пифагоровы штаны
Книга рекордов
Дерево
Провод
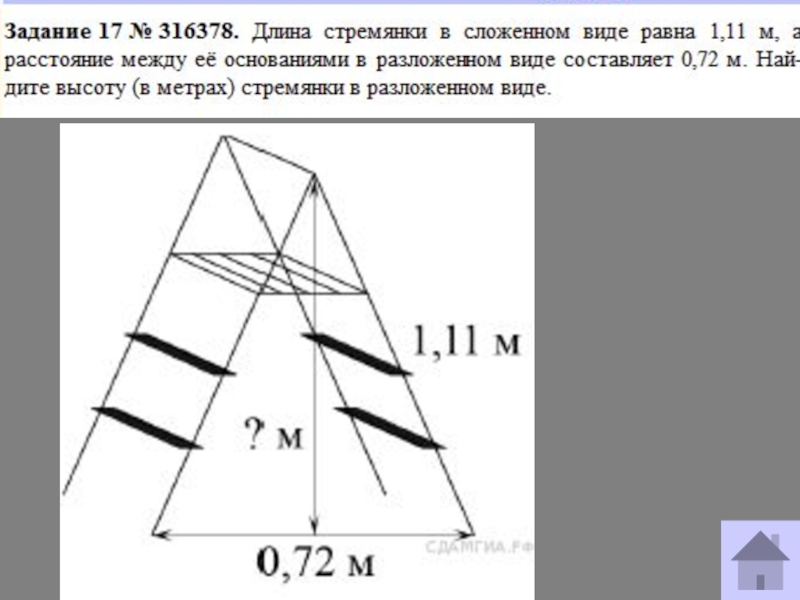
Стремянка
Крепость
Ступени
Итог
Флаг
Лестница
Слайд 220 в. до н.э.
6 в. до н.э.
Дано: с2 = а2 +
в2
Доказать: треугольник –прямоугольный
Доказать: треугольник –прямоугольный
Дано: треугольник –прямоугольный
Доказать: с2 = а2 + в2
Слайд 9Задача Леонарда
Пизанского, XIII век.
Две башни в равнине находятся на расстоянии
60 локтей одна от другой. Высота первой башни 50 локтей, высота второй 40 локтей. Между башнями находится колодец, одинаково удалённый от вершин башен. Как далеко находится колодец от основания каждой башни?
Слайд 11Задача древнекитайского ученого
Цзинь Киу - чау, 1250 лет до н.э.
В
центре квадратного пруда, имеющего 10 футов в длину и ширину, растёт тростник , возвышающийся на 1 фут над поверхностью воды. Если его пригнуть к берегу, к середине стороны пруда, то он достигнет своей верхушкой берега. Какова глубина пруда?