- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике теме: Бином Ньютона, треугольник Паскаля
Содержание
- 1. Презентация по математике теме: Бином Ньютона, треугольник Паскаля
- 2. Слайд 2
- 3. Бином Ньютона – это формула, выражающая выражение
- 4. самой известной математической работой Блеза Паскаля является
- 5. Слайд 5
- 6. треугольник Паскаля был известен
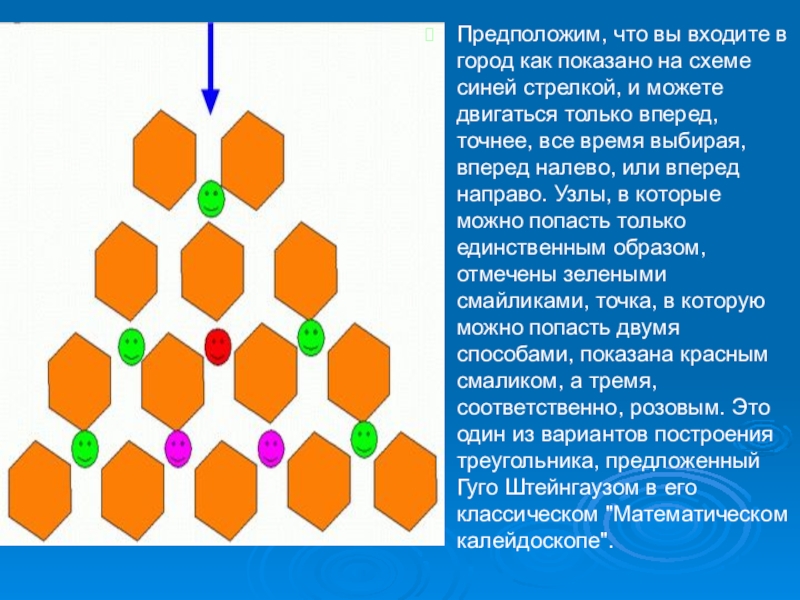
- 7. Предположим, что вы входите в город как
- 8. Слайд 8
- 9. А еще проще объясняют устройство треугольника Паскаля
- 10. Четность числа легко определить
- 11. Движемся далее - пробуем проверять
- 12. назначим три переменных ,ответственных, соответственно,
- 13. Треугольник Паскаля-бесконечный треугольник из чисел
- 14. Факториал натурального числа — произведение всех чисел
- 15. Слайд 15
- 16. Слайд 16
- 17. Слайд 17
- 18. Слайд 18
- 19. Слайд 19
- 20. Слайд 20
- 21. Слайд 21
- 22. Слайд 22
- 23. Слайд 23
- 24. Слайд 24
- 25. Слайд 25
- 26. Слайд 26
- 27. Слайд 27
- 28. Слайд 28
Слайд 3Бином Ньютона – это формула, выражающая выражение (a + b)n в
Широко известные формулы сокращенного умножения квадрата суммы и разности, куба суммы и разности, являются частными случаями бинома Ньютона.
Когда степень бинома невысока, коэффициенты многочлена могут быть найдены не расчетом по формуле количества сочетаний, а с помощью так называемого треугольника Паскаля. (Блез Паскаль (1623 – 1662) – французский математик).
Бином Ньютона – это формула, выражающая выражение (a + b)n в виде многочлена.
Широко известные формулы сокращенного умножения квадрата суммы и разности, куба суммы и разности, являются частными случаями бинома Ньютона.
Когда степень бинома невысока, коэффициенты многочлена могут быть найдены не расчетом по формуле количества сочетаний, а с помощью так называемого треугольника Паскаля. (Блез Паскаль (1623 – 1662) – французский математик).
Слайд 4самой известной математической работой Блеза Паскаля является трактат об "арифметическом треугольнике",
самой известной математической работой Блеза Паскаля является трактат об "арифметическом треугольнике", образованном биномиальными коэффициентами (треугольник Паскаля), который имеет применение в теории вероятностей и обладает удивительными и занимательными свойствами .
Слайд 6 треугольник Паскаля был известен задолго до 1653 года
Так, этот треугольник воспроизведен на титульном листе учебника арифметики,
написанном в начале XVI Петром Апианом, астрономом из Ингольтштадского университета. Изображен треугольник и на иллюстрации в книге одного китайского математика, выпущенной в 1303 году. Омар Хайям, бывший не только философом и поэтом, но и математиком, знал о существовании треугольника около 1100 года, в свою очередь, заимствовав его из более ранних китайских или индийских источников. Мартин Гарднер пишет в книге "Математические новеллы" (М., Мир, 1974): "Треугольник Паскаля так прост, что выписать его сможет даже десятилетний ребенок. В тоже время он таит в себе неисчерпаемые сокровища и связывает воедино различные аспекты математики, не имеющие на первый взгляд между собой ничего общего. Столь необычные свойства позволяют считать треугольник Паскаля одной из наиболее изящных схем во всей математике
Слайд 7
Предположим, что вы входите в город как показано на схеме синей
Слайд 9А еще проще объясняют устройство треугольника Паскаля слова: каждое число равно
Суммы чисел, стоящих вдоль не столь круто падающих диагоналей (на рисунке отмечены красными линиями) образуют хорошо известную постоянным читателям последовательность Фибоначчи
Слайд 10 Четность числа легко определить сравнением остатка от деления на два с
Слайд 11 Движемся далее - пробуем проверять не четность, а остаток от деления
Слайд 12 назначим три переменных ,ответственных, соответственно, за красную, зеленую и синюю составляющую
И вот результат работы программы. Не правда ли красиво? Видны красные треугольные "зоны Серпинского", которые, накладываясь на зеленые окошки от девяток, дают желтые зоны, а с синими участками от деления на 11 дают сиреневые участки.