.
Выполнил: Автомонов Николай
Руководитель: Вологжанина Е.И.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Сечения (10 класс)
Содержание
- 1. Презентация по математике Сечения (10 класс)
- 2. Выберите фигуру, сведения о которой вы хотите получить:ВыходПирамидаЧетырехугольнаяТреугольнаяПризмаЧетырехугольнаяТреугольнаяПятиугольнаяКуб
- 3. ПирамидаПирамида-многогранник, основание которого-многоугольник, а боковыми гранями являются
- 4. Пирамида треугольнаяABCВ данной пирамиде плоскость сечения проходит
- 5. Пирамида треугольнаяABCдалееВ данной пирамиде плоскость сечения проходит
- 6. Пирамида треугольнаяαПри таком взаиморасположении плоскости и пирамиды
- 7. Пирамида четырехугольнаяВ данной пирамиде плоскость сечения проходит
- 8. Пирамида четырехугольнаяВ данной пирамиде плоскость сечения проходит
- 9. Пирамида четырехугольнаядалееABCВ данной пирамиде плоскость сечения проходит
- 10. Пирамида четырехугольнаядалееABCВ данной пирамиде плоскость сечения проходит
- 11. Пирамида четырехугольнаяК выбору фигурыК сечениям треугольной пирамидыαПри
- 12. ПризмаПризма-многогранник, имеющий 2 основания-многоугольника с боковыми гранями-прямоугольниками.В
- 13. Треугольная призмадалееABCВ данной призме плоскость сечения проходит
- 14. Треугольная призмадалееABCВ данной призме плоскость сечения проходит
- 15. Треугольная призмадалееABCВ данной призме плоскость сечения проходит через 3 вершины, не лежащих в одной плоскости.
- 16. Треугольная призмаABCК выбору фигурыК перечню сечений призмВ
- 17. Четырехугольная призмадалееABCВ данной призме плоскость сечения проходит через точки, лежащие на смежных ребрах верхнего основания.
- 18. Четырехугольная призмаВ данной призме плоскость сечения проходит через 3 вершины, не лежащие в одной плоскости.далееABC
- 19. Четырехугольная призмадалееABCВ данной призме плоскость сечения проходит
- 20. Четырехугольная призмаABCК выбору фигурыК перечню сечений призмВ
- 21. КубКуб- четырехугольная правильная призма, гранями которого являются 8 равных квадратов.ABCA1B1C1D1К сечениям куба
- 22. КубВ кубе плоскость сечения проходит через точки
- 23. КубABCдалееВ кубе плоскость сечения проходит через точки, лежащие на смежных ребрах верхнего основания.
- 24. КубABCК выбору фигурыК перечню сечений призмВ кубе
- 25. Пятиугольная призмадалееABCВ данной призме плоскость сечения проходит через точки, лежащие на смежных ребрах верхнего основания.
- 26. Пятиугольная призмаВ данной призме плоскость сечения проходит
- 27. Пятиугольная призмаВ данной призме плоскость сечения проходит
Выберите фигуру, сведения о которой вы хотите получить:ВыходПирамидаЧетырехугольнаяТреугольнаяПризмаЧетырехугольнаяТреугольнаяПятиугольнаяКуб
Слайд 2Выберите фигуру, сведения о
которой вы хотите получить:
Выход
Пирамида
Четырехугольная
Треугольная
Призма
Четырехугольная
Треугольная
Пятиугольная
Куб
Слайд 3Пирамида
Пирамида-многогранник, основание которого-многоугольник, а боковыми гранями являются треугольники, имеющие общую вершину,
не лежащую в плоскости многоугольника.
A
B
C
S
К сечениям треугольной
пирамиды
A
B
C
S
К сечениям четырехугольной
пирамиды
D
Слайд 4Пирамида треугольная
A
B
C
В данной пирамиде плоскость сечения проходит через 2 ее вершины
и точку, лежащую на противоположном ребре пирамиды
далее
Слайд 5Пирамида треугольная
A
B
C
далее
В данной пирамиде плоскость сечения проходит через 2 вершины, лежащие
на ребрах основания и вершину пирамиды.
Слайд 6Пирамида треугольная
α
При таком взаиморасположении плоскости и пирамиды получается новая фигура- усеченная
треугольная пирамида.
К сечениям четырехугольной
пирамиды
К выбору фигуры
Слайд 7Пирамида четырехугольная
В данной пирамиде плоскость сечения проходит через вершину пирамиды и
точки, лежащие на ребрах ее основания.
A
B
C
далее
Слайд 8Пирамида четырехугольная
В данной пирамиде плоскость сечения проходит через 2 противолежащие вершины
основания и вершину, не лежащую в плоскости этих двух точек- такое сечение пирамиды называется диагональным.
A
B
C
далее
Слайд 9Пирамида четырехугольная
далее
A
B
C
В данной пирамиде плоскость сечения проходит через 2 точки, лежащие
на противоположных ребрах основания и вершину пирамиды.
Слайд 10Пирамида четырехугольная
далее
A
B
C
В данной пирамиде плоскость сечения проходит через 2 точки, лежащие
на ребрах основания и точку, лежащую на боковом ребре пирамиды.
Слайд 11Пирамида четырехугольная
К выбору фигуры
К сечениям
треугольной пирамиды
α
При таком взаиморасположении плоскости и
пирамиды получается новая фигура- усеченная четырехугольная пирамида.
Слайд 12Призма
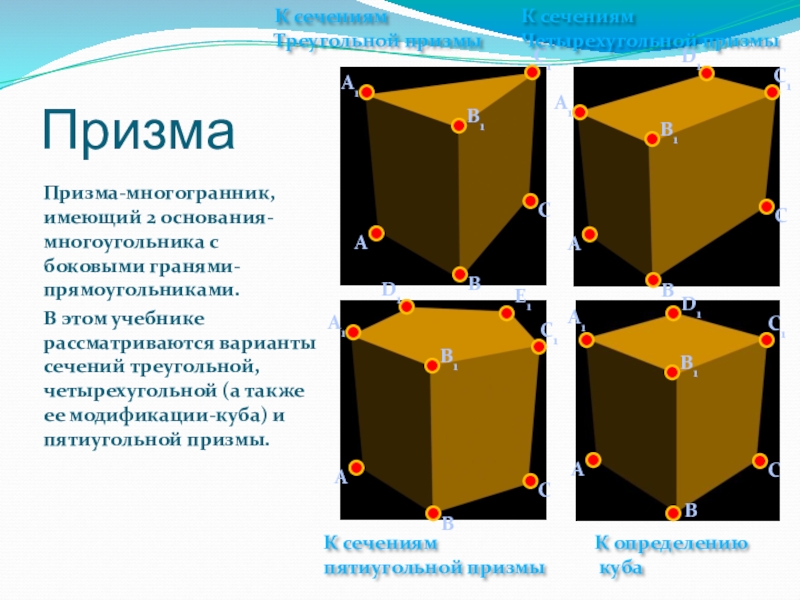
Призма-многогранник, имеющий 2 основания-многоугольника с боковыми гранями-прямоугольниками.
В этом учебнике рассматриваются варианты
сечений треугольной, четырехугольной (а также ее модификации-куба) и пятиугольной призмы.
A
B
C
A1
B1
C1
D1
К определению
куба
A
B
C
A1
B1
C1
D1
A
B
C
A1
B1
C1
E1
К сечениям
Треугольной призмы
К сечениям
Четырехугольной призмы
К сечениям
пятиугольной призмы
A
C
B1
C1
B
D1
A1
Слайд 13Треугольная призма
далее
A
B
C
В данной призме плоскость сечения проходит через точки, расположенные на
смежных ребрах верхнего основания пирамиды.
Слайд 14Треугольная призма
далее
A
B
C
В данной призме плоскость сечения проходит через 2 точки, лежащие
на ребрах верхнего основания и через одну- нижнего.
Слайд 15Треугольная призма
далее
A
B
C
В данной призме плоскость сечения проходит через 3 вершины, не
лежащих в одной плоскости.
Слайд 16Треугольная призма
A
B
C
К выбору фигуры
К перечню сечений призм
В данной призме плоскость сечения
проходит через точки, лежащие на параллельных ребрах и вершину призмы.
Слайд 17Четырехугольная призма
далее
A
B
C
В данной призме плоскость сечения проходит через точки, лежащие на
смежных ребрах верхнего основания.
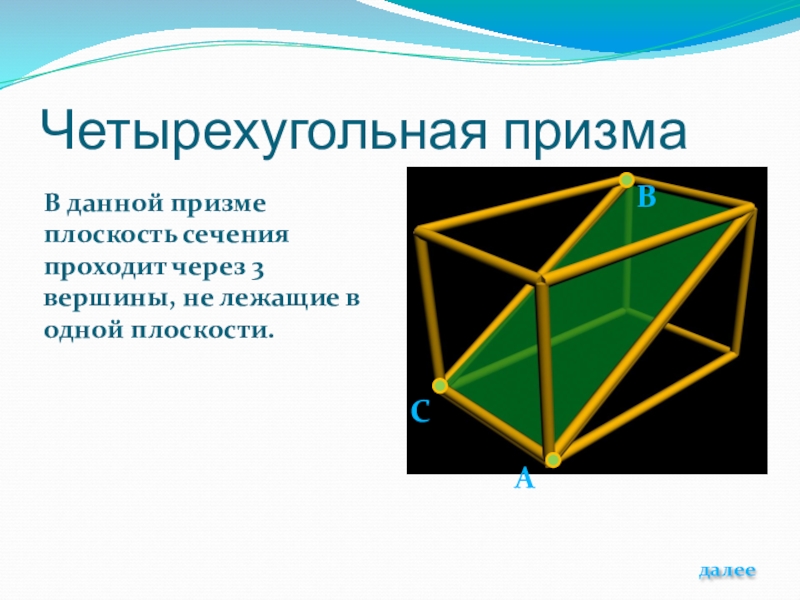
Слайд 18Четырехугольная призма
В данной призме плоскость сечения проходит через 3 вершины, не
лежащие в одной плоскости.
далее
A
B
C
Слайд 19Четырехугольная призма
далее
A
B
C
В данной призме плоскость сечения проходит через 2 параллельные диагонали
призмы- такое сечение призмы называется диагональным.
Слайд 20Четырехугольная призма
A
B
C
К выбору фигуры
К перечню сечений призм
В данной призме плоскость сечения
проходит через точки на параллельных ребрах, при этом, она будет параллельна грани призмы.
Слайд 21Куб
Куб- четырехугольная правильная призма, гранями которого являются 8 равных квадратов.
A
B
C
A1
B1
C1
D1
К сечениям
куба
Слайд 22Куб
В кубе плоскость сечения проходит через точки на параллельных ребрах, при
этом, она будет параллельна грани куба.
A
B
C
далее
Слайд 23Куб
A
B
C
далее
В кубе плоскость сечения проходит через точки, лежащие на смежных ребрах
верхнего основания.
Слайд 24Куб
A
B
C
К выбору фигуры
К перечню сечений призм
В кубе плоскость сечения проходит через
точки на параллельных ребрах, при этом, она не будет параллельна грани куба.
Слайд 25Пятиугольная призма
далее
A
B
C
В данной призме плоскость сечения проходит через точки, лежащие на
смежных ребрах верхнего основания.
Слайд 26Пятиугольная призма
В данной призме плоскость сечения проходит через 2 параллельные диагонали
призмы- такое сечение призмы называется диагональным.
далее
A
B
C
Слайд 27Пятиугольная призма
В данной призме плоскость сечения проходит через 2 вершины и
боковое ребро призмы.
A
B
C
К выбору фигуры
К перечню сечений призм
