Выполнила Позднышева С.В. ,учитель математики специализированной школы №11.
Г. Свердловск
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
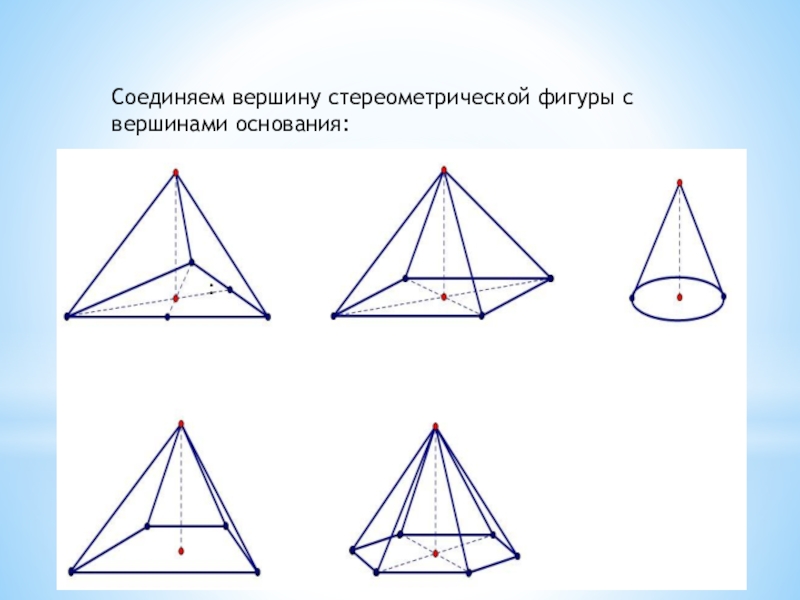
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике: Решение и оформление стереометрических задач профильного уровня при подготовке к ГИА и ЕГЭ по математике в 11 классе Э
Содержание
- 1. Презентация по математике: Решение и оформление стереометрических задач профильного уровня при подготовке к ГИА и ЕГЭ по математике в 11 классе Э
- 2. При подготовке к сдаче ГИА и ЕГЭ
- 3. При решении задач очень важно изобразить
- 4. Свойства параллельного проектирования при построении стереометрического чертежаВнимание!
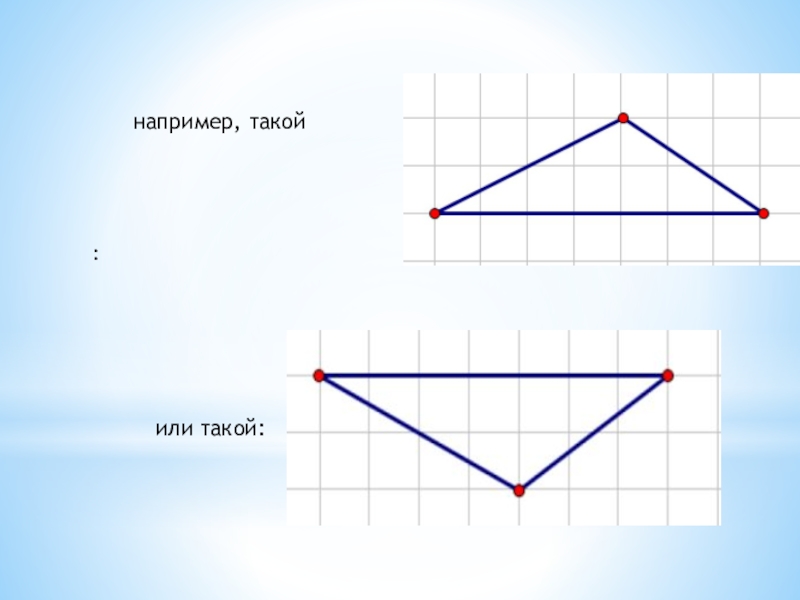
- 5. :или такой:например, такой
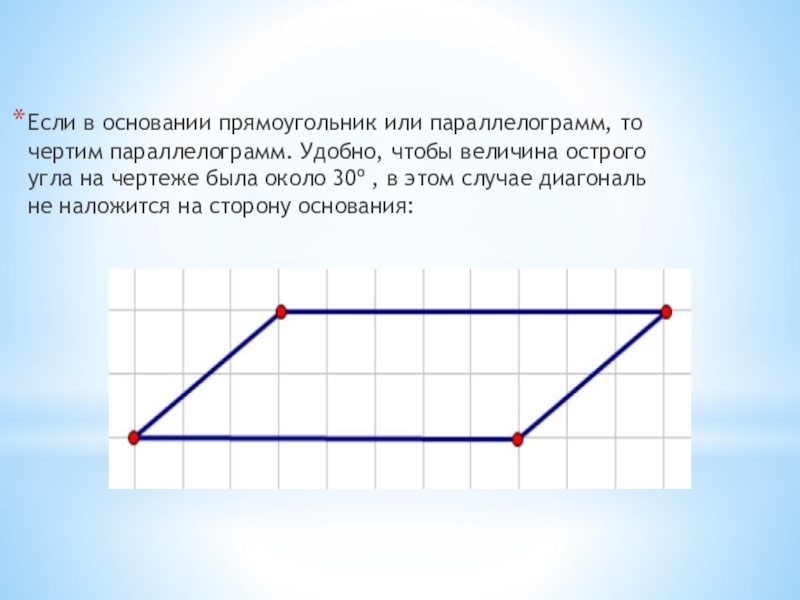
- 6. Если в основании прямоугольник или параллелограмм, то
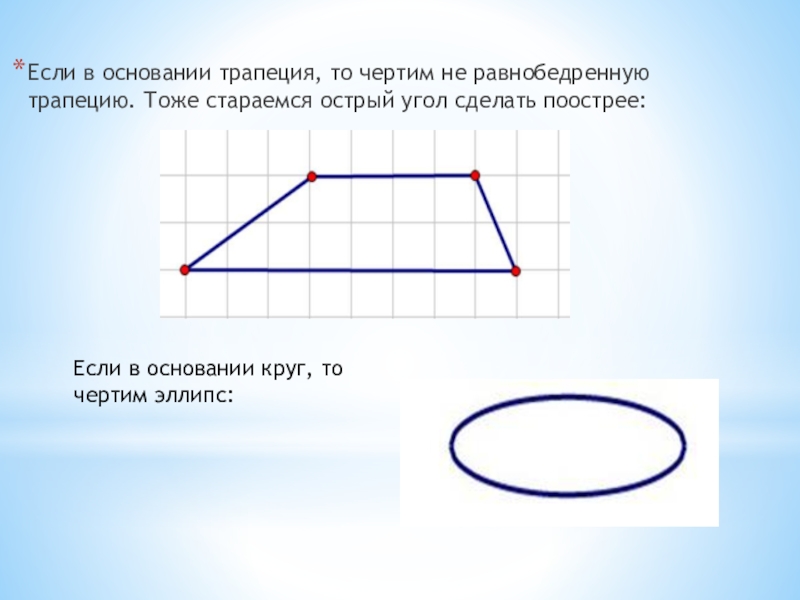
- 7. Если в основании трапеция, то чертим не
- 8. Если в основании правильный шестиугольник, то чертим
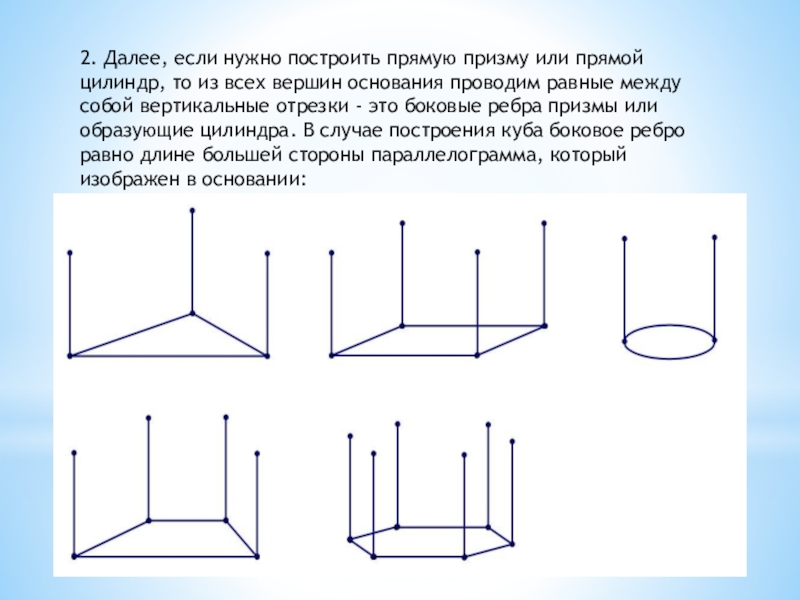
- 9. 2. Далее, если нужно построить прямую призму
- 10. Слайд 10
- 11. Слайд 11
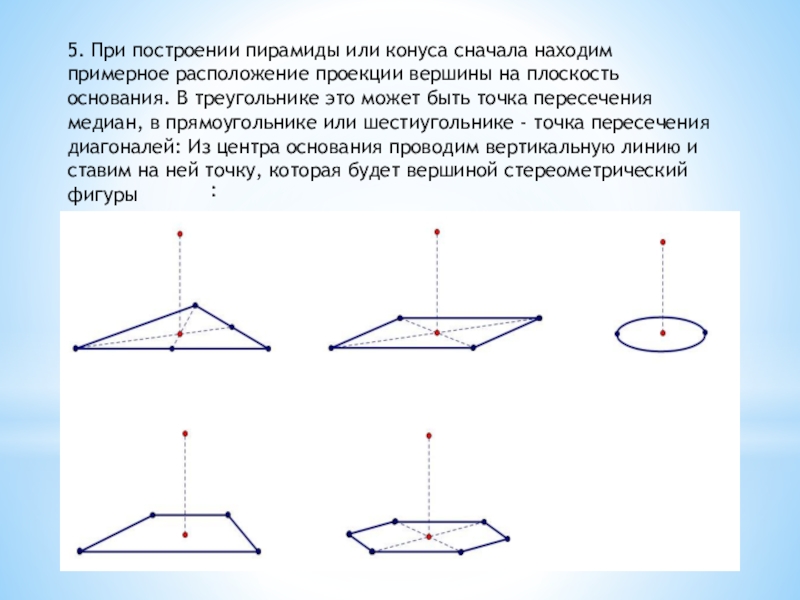
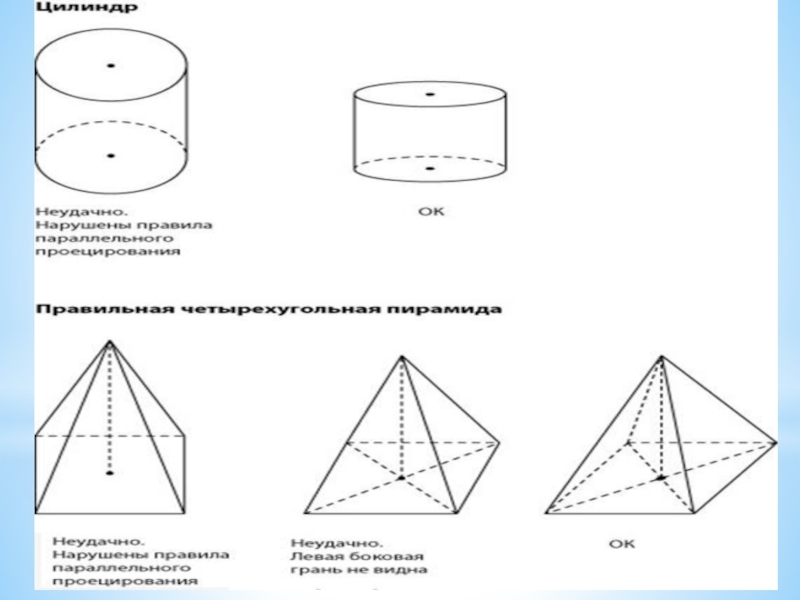
- 12. 5. При построении пирамиды или конуса сначала
- 13. :Соединяем вершину стереометрической фигуры с вершинами основания:
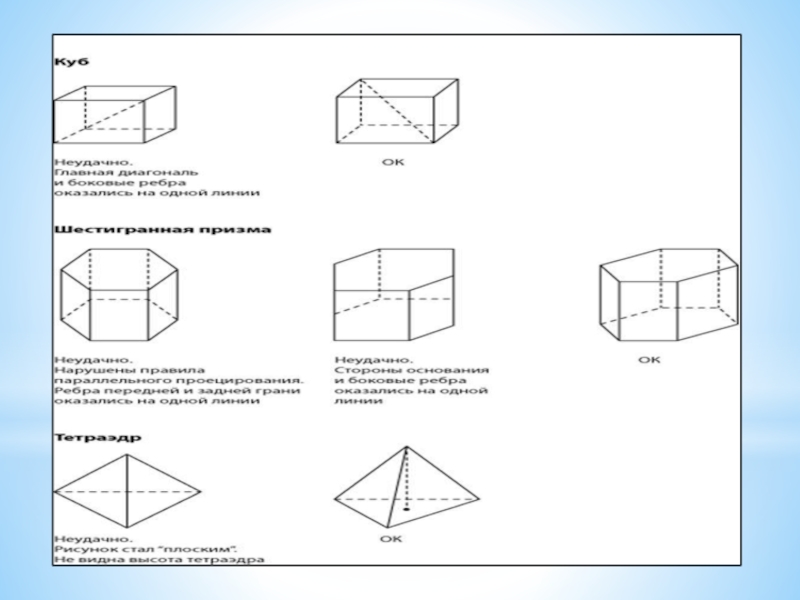
- 14. Приведем примеры удачных и неудачных чертежей. Мы рисуем чертеж крупным,
- 15. Слайд 15
- 16. Слайд 16
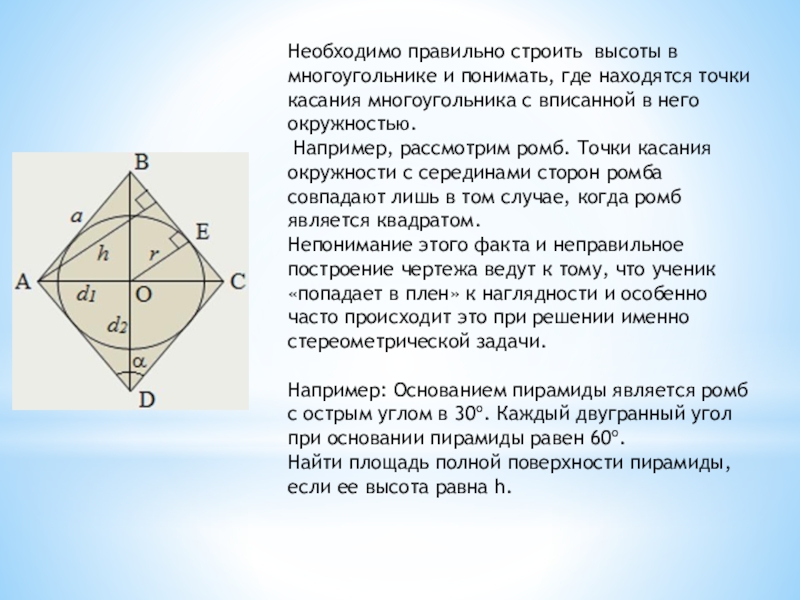
- 17. Необходимо правильно строить высоты в многоугольнике и
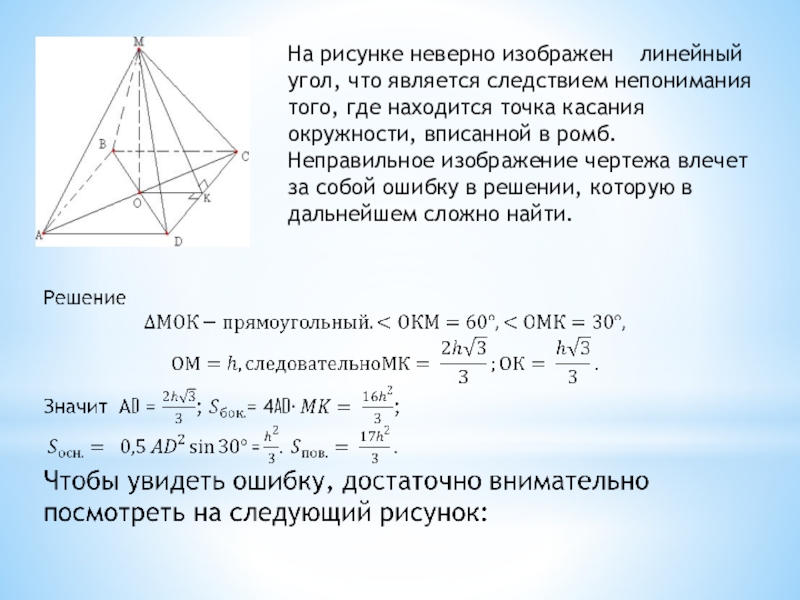
- 18. На рисунке неверно изображен линейный угол,
- 19. Слайд 19
- 20. Теорема о трех перпендикулярахИмеем плоскость α .
- 21. Слайд 21
- 22. Чтобы легко справиться с решением задач на
- 23. СПАСИБО ЗА ВНИМАНИЕ!
Слайд 1Мастер-класс по теме: «Решение и оформление стереометрических задач профильного уровня при
Слайд 2При подготовке к сдаче ГИА и ЕГЭ учащиеся стараются проигнорировать задания
Все это ставит перед учителем математики сложную задачу: за короткое время постараться повторить с учащимися достаточно большой объем материала, среди которого и формулы, и теоремы для обоснования рисунка и решения задачи, научить правильно изображать геометрические фигуры , используя свойства параллельного проектирования, так чтобы рисунок был наглядным и мог бы действительно помочь в решении задачи.
Кроме этого учитель имеет как минимум три различных подхода к подготовке учащихся к экзаменам:
- Коллективное решение задачи на уроке;
- Самостоятельное решение задачи учащимися;
- Перед тем как предложить решать задачу самостоятельно, рассмотреть отдельные ее части, чтобы учащиеся, начав самостоятельные действия, не оказались в ситуации, когда они ничего не помнят и не представляют как приступить к ее решению
Слайд 3 При решении задач очень важно изобразить хороший чертеж. Для этого
Слайд 4Свойства параллельного проектирования при построении стереометрического чертежа
Внимание! При параллельном проектирование не
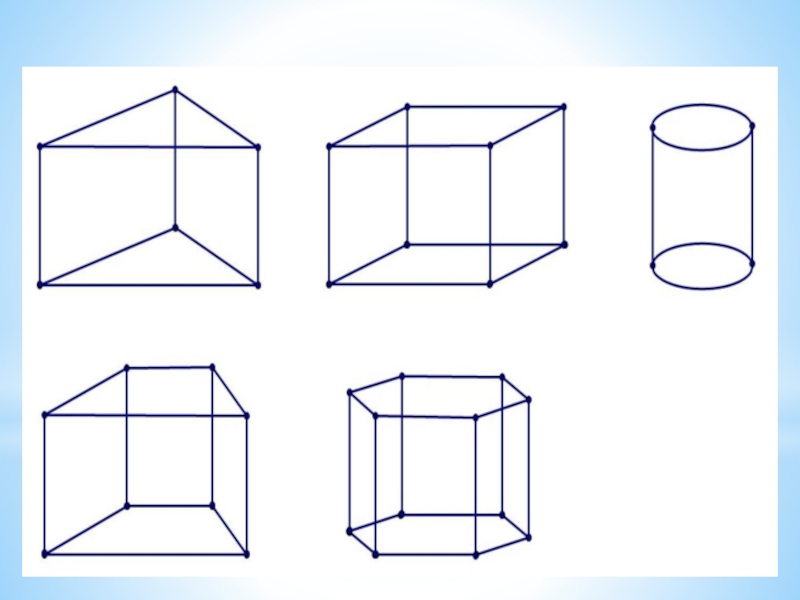
При изображении стандартных геометрических тел на плоскости нужно следить за тем, чтобы ребра и диагонали были все видны и не накладывались друг на друга.
В общем случае удобно строить в такой последовательности.
1. Начинаем с основания фигуры.
Если в основании треугольник, то вне зависимости от вида треугольника рисуем тупоугольный не равнобедренный треугольник,
Слайд 6Если в основании прямоугольник или параллелограмм, то чертим параллелограмм. Удобно, чтобы
Слайд 7Если в основании трапеция, то чертим не равнобедренную трапецию. Тоже стараемся
Если в основании круг, то чертим эллипс:
Слайд 8Если в основании правильный шестиугольник, то чертим проекцию правильного шестиугольника. Следим
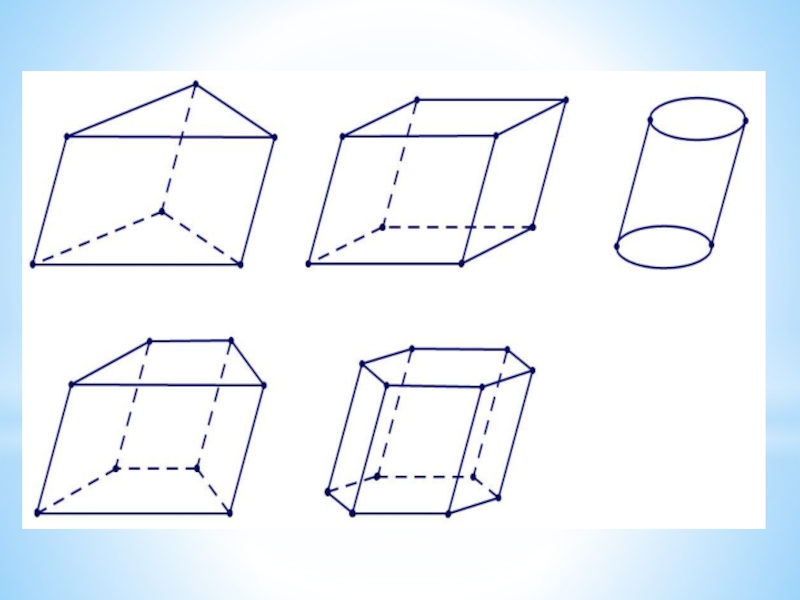
Слайд 92. Далее, если нужно построить прямую призму или прямой цилиндр, то
Слайд 125. При построении пирамиды или конуса сначала находим примерное расположение проекции
:
Слайд 14Приведем примеры удачных и неудачных чертежей.
Мы рисуем чертеж крупным, чтобы на нем всё было
Видимые линии изображаем сплошными, невидимые —пунктирными. Если вы решаете задачу векторно-координатным методом, ставьте рядом с точками их координаты. Это удобно.
Иногда одного чертежа недостаточно. Чаще всего для решения задач по стереометрии, кроме «объемного» чертежа, нужен один или несколько плоских.
Слайд 17Необходимо правильно строить высоты в многоугольнике и понимать, где находятся точки
Например, рассмотрим ромб. Точки касания окружности с серединами сторон ромба совпадают лишь в том случае, когда ромб является квадратом.
Непонимание этого факта и неправильное построение чертежа ведут к тому, что ученик «попадает в плен» к наглядности и особенно часто происходит это при решении именно стереометрической задачи.
Например: Основанием пирамиды является ромб с острым углом в 30º. Каждый двугранный угол при основании пирамиды равен 60º.
Найти площадь полной поверхности пирамиды, если ее высота равна h.
Слайд 18На рисунке неверно изображен линейный угол, что является следствием непонимания
Слайд 20Теорема о трех перпендикулярах
Имеем плоскость α . В плоскости α лежит
АН – перпендикуляр к плоскости α, АМ – наклонная,
МН - проекция наклонной АМ на плоскость α.
По теореме о трех перпендикулярах, наклонная перпендикулярна к прямой b тогда и только тогда, когда ее проекция перпендикулярна к прямой b.
В теореме идет речь трех перпендикулярах. Укажем их:
АH – это перпендикуляр к плоскости α, а значит, к прямой b.
HМ – проекция, перпендикуляр к прямой b.
АМ – наклонная, перпендикуляр к прямой b.
Слайд 22Чтобы легко справиться с решением задач на шар, вписанный в пирамиду,
Шар вписан в пирамиду (или сфера вписана в пирамиду) — значит, шар (сфера) касаются каждой грани пирамиды. Плоскости, содержащие грани пирамиды, являются касательными плоскостями шара. Отрезки, соединяющие центр шара с точками касания, перпендикуляры к касательным плоскостям. Их длины равны радиусу шара. Центр вписанного в пирамиду шара — точка пересечения биссекторных плоскостей двугранных углов при основании (то есть плоскостей, делящих эти углы пополам).
Чаще всего в задачах речь идет о шаре, вписанном в правильную пирамиду. Шар можно вписать в любую правильную пирамиду. Центр шара в этом случае лежит на высоте пирамиды. При решении задачи удобно провести сечение пирамиды и шара плоскостью, проходящей через апофему и высоту пирамиды. Если пирамида четырехугольная или шестиугольная, сечение представляет собой равнобедренный треугольник, боковые стороны которого — апофемы, а основание — диаметр вписанной в основание окружности.