- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Правильные многогранники
Содержание
- 1. Презентация по математике Правильные многогранники
- 2. «Правильных многогранников вызывающе мало, но этот весьма
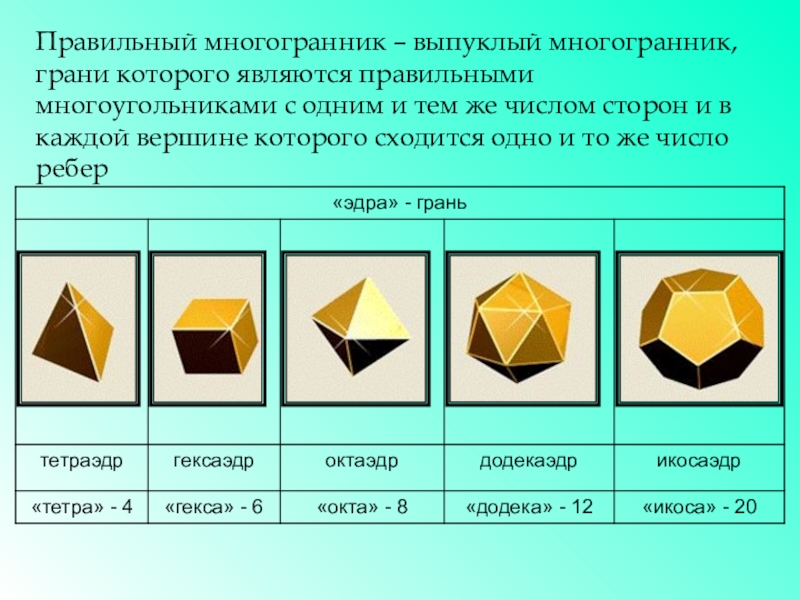
- 3. Правильный многогранник – выпуклый многогранник, грани которого
- 4. Поверхность тетраэдра состоит из четырех равносторонних треугольников, сходящихся в каждой вершине по триТЕТРАЭДР
- 5. Куб имеет шесть квадратных граней, сходящихся в каждой вершине по триКУБ (ГЕКСАЭДР)
- 6. Октаэдр имеет восемь треугольных граней, сходящихся в каждой вершине по четыре ОКТАЭДР
- 7. Додекаэдр имеет двенадцать пятиугольных граней, сходящихся в вершинах по три ДОДЕКАЭДР
- 8. Поверхность икосаэдра состоит из двадцати равносторонних треугольников, сходящихся в каждой вершине по пять ИКОСАЭДР
- 9. Платоновы тела
- 10. Тетраэдр олицетворял огонь, поскольку его вершина устремлена
- 11. вселеннаядодекаэдрПятый многогранник – додекаэдр символизировал весь
- 12. Кубок КеплераИоганн Кеплер, великий немецкий астроном и
- 13. Согласно этому предположению, вокруг сферы Меркурия описан октаэдр.
- 14. Сегодня можно с уверенностью утверждать, что расстояния
- 15. Теорема ЭйлераВ правильном многограннике число вершин плюс
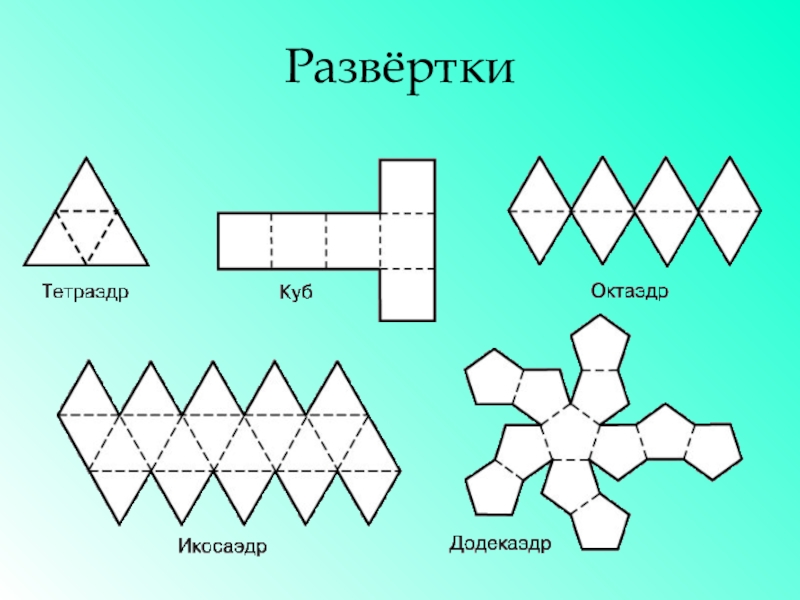
- 16. Развёртки
«Правильных многогранников вызывающе мало, но этот весьма скромный по численности отряд сумел пробраться в самые глубины различных наук»
Слайд 2«Правильных многогранников вызывающе мало, но этот весьма скромный по численности отряд
сумел пробраться в самые глубины различных наук»
Л. Кэррол
Л. Кэррол
Слайд 3Правильный многогранник – выпуклый многогранник, грани которого являются правильными многоугольниками с
одним и тем же числом сторон и в каждой вершине которого сходится одно и то же число ребер
Слайд 4Поверхность тетраэдра состоит из четырех равносторонних треугольников, сходящихся в каждой вершине
по три
ТЕТРАЭДР
Слайд 8Поверхность икосаэдра состоит из двадцати равносторонних треугольников, сходящихся в каждой вершине
по пять
ИКОСАЭДР
Слайд 10Тетраэдр олицетворял огонь, поскольку его вершина устремлена вверх, как у разгоревшегося
пламени
огонь
тетраэдр
Куб – самая устойчивая из фигур – землю
Икосаэдр – как самый обтекаемый – воду
вода
икосаэдр
воздух
октаэдр
Октаэдр – воздух
земля
гексаэдр
В наше время эту систему можно сравнить с четырьмя состояниями вещества: твёрдым, жидким, газообразным и пламенным.
Слайд 11
вселенная
додекаэдр
Пятый многогранник – додекаэдр символизировал весь мир и почитался главнейшим. Это
была одна из первых попыток ввести в науку идею систематизации.
Слайд 12Кубок Кеплера
Иоганн Кеплер, великий немецкий астроном и математик (1571-1630 г.г.), для
которого правильные многогранники были любимым предметом изучения, предположил, что существует связь между пятью правильными многогранниками и шестью открытыми к тому времени планетами Солнечной системы.
Слайд 13Согласно этому предположению, вокруг сферы Меркурия описан октаэдр. Этот октаэдр вписан в сферу
Венеры, вокруг которой описан икосаэдр. Вокруг икосаэдра описана сфера Земли, а вокруг этой сферы - додекаэдр. Додекаэдр вписан в сферу Марса, вокруг которой описан тетраэдр. Вокруг тетраэдра описана сфера Юпитера, вписанная в куб. Наконец, вокруг куба описана сфера Сатурна.
Такая модель Солнечной системы получила название «Космического кубка» Кеплера. Результаты своих вычислений учёный опубликовал в книге «Тайна мироздания». Он считал, что тайна Вселенной раскрыта. Год за годом он уточнял свои наблюдения, перепроверял данные коллег, но наконец нашёл в себе силы отказаться от заманчивой гипотезы. Однако её следы просматриваются в третьем законе Кеплера, где говорится о кубах средних расстояний от Солнца.
Такая модель Солнечной системы получила название «Космического кубка» Кеплера. Результаты своих вычислений учёный опубликовал в книге «Тайна мироздания». Он считал, что тайна Вселенной раскрыта. Год за годом он уточнял свои наблюдения, перепроверял данные коллег, но наконец нашёл в себе силы отказаться от заманчивой гипотезы. Однако её следы просматриваются в третьем законе Кеплера, где говорится о кубах средних расстояний от Солнца.
Слайд 14Сегодня можно с уверенностью утверждать, что расстояния между планетами и их
число никак не связаны с многогранниками. Конечно, структура Солнечной системы не является случайной, но истинные причины, по которым она устроена так, а не иначе, до сих пор не известны. Идеи Кеплера оказались ошибочными, но без гипотез, иногда самых неожиданных, казалось бы бредовых, не может существовать наука.
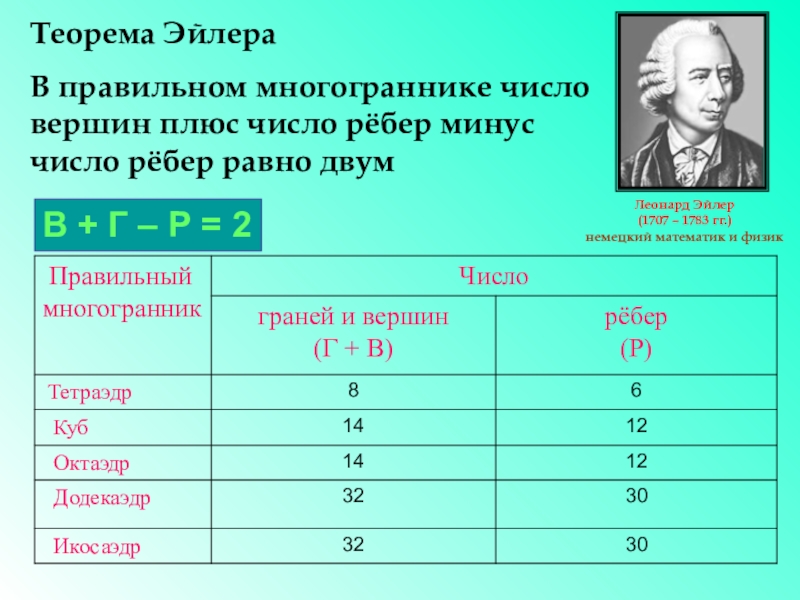
Слайд 15Теорема Эйлера
В правильном многограннике число вершин плюс число рёбер минус число
рёбер равно двум
В + Г – Р = 2
Леонард Эйлер
(1707 – 1783 гг.)
немецкий математик и физик
