Белгородской области Байдукова Г.Г.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике по теме Векторы (11 класс)
Содержание
- 1. Презентация по математике по теме Векторы (11 класс)
- 2. Понятие вектора в пространствеПонятие вектораВектор – это
- 3. Сложение и вычитание векторов. Сложение и вычитание
- 4. Умножение вектора на числоПроизведением ненулевого вектора а
- 5. Компланарные векторыВекторы называются компланарными, если при откладывании
- 6. Разложение вектора по трем некомпланарным векторам. Если
- 7. Координаты точки и координаты вектора.Если через точку
- 8. Координаты вектора. Связь между координатами векторов и
Понятие вектора в пространствеПонятие вектораВектор – это отрезок, у которого есть начало и конец.Любая точка это вектор.Нулевой вектор – когда начало совпадает с концом.Длиной вектора называется длина отрезка, которым обозначен вектор.Два ненулевых вектора называются коллинеарными, если
Слайд 1Буклет-справочник по теме «ВЕКТОРЫ» (шпаргалка)
Подготовила:
Учитель математики МОУ «СОШ №1» г.Валуйки
Слайд 2Понятие вектора в пространстве
Понятие вектора
Вектор – это отрезок, у которого есть
начало и конец.
Любая точка это вектор.
Нулевой вектор – когда начало совпадает с концом.
Длиной вектора называется длина отрезка, которым обозначен вектор.
Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых.
Любая точка это вектор.
Нулевой вектор – когда начало совпадает с концом.
Длиной вектора называется длина отрезка, которым обозначен вектор.
Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых.
Равенство векторов
Векторы называются равными, если они сонаправлены и их длины равны.
От любой точки можно отложить вектор, равный данному и при том только один.
.
с
b
a
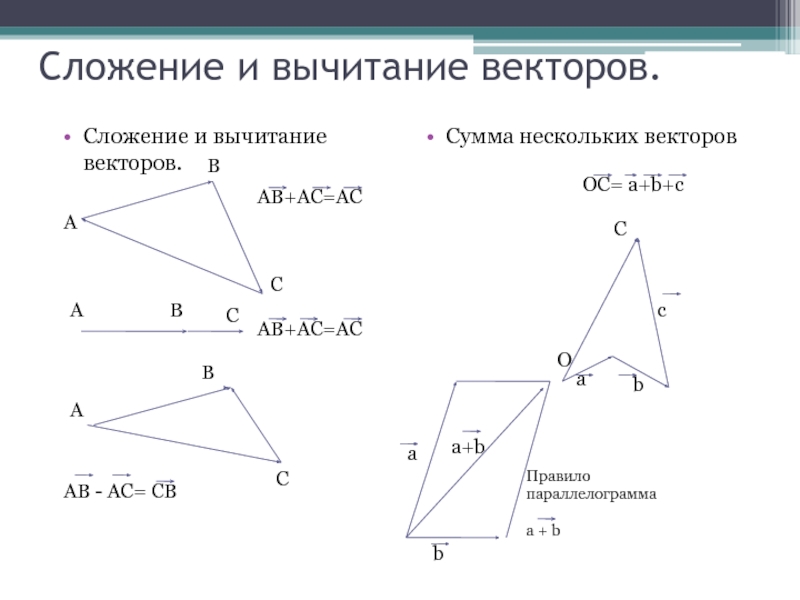
Слайд 3Сложение и вычитание векторов.
Сложение и вычитание векторов.
Сумма нескольких векторов
АВ+АС=АС
АВ+АС=АС
АВ - АС=
CB
Правило параллелограмма
a + b
OC= a+b+c
A
B
C
A
A
B
B
C
C
C
O
a
b
c
a
b
a+b
Слайд 4Умножение вектора на число
Произведением ненулевого вектора а на число k называется
такой вектор b, длина которого равна k*a , причем векторы a и b сонаправлены при k больше 0
Произведением нулевого вектора на любое число считается нулевой вектор.
Для любого числа k и любого вектора а векторы а и kа коллинеарны.
Произведение любого вектора на число нуль есть нулевой вектор.
Произведением нулевого вектора на любое число считается нулевой вектор.
Для любого числа k и любого вектора а векторы а и kа коллинеарны.
Произведение любого вектора на число нуль есть нулевой вектор.
Для любых векторов а, b и любых чисел k, l справедливы равенства:
(kl)a=k(la)
k(a+b)=ka+kb
(k+l)a=ka+la
Если векторы а и b коллинеарны, и а=0, то существует такое число k, что b=ka
Слайд 5Компланарные векторы
Векторы называются компланарными, если при откладывании их от одной и
той же точки будет лежать в одной плоскости.
Если вектор с можно разложить по векторам a и b, то есть представить в виде с = xa-yb, где х и у – некоторые числа, то векторы а, b и с компланарны.
Если вектор с можно разложить по векторам a и b, то есть представить в виде с = xa-yb, где х и у – некоторые числа, то векторы а, b и с компланарны.
Слайд 6Разложение вектора по трем некомпланарным векторам.
Если вектор р представлен в виде
р=ха+yb+zc, где x, y, z – некоторые числа , то говорят, что вектор р разложен по векторам a, b, c; а числа x, y, z – коэффициенты разложения.
Любой вектор можно разложить по трем данным некомпланарным векторам, причем коэффициенты расположения определяются единственным образом.
Любой вектор можно разложить по трем данным некомпланарным векторам, причем коэффициенты расположения определяются единственным образом.
Слайд 7Координаты точки и координаты вектора.
Если через точку пространства проведены попарно перпендикулярные
прямые, на каждой из них выбрано направление и выбрана единица измерения отрезков, то говорят, что задана прямоугольная система координат в пространстве.
Прямые с выбранными на них направлениями называют осями координат, а их общая точка – началом координат.
Прямые с выбранными на них направлениями называют осями координат, а их общая точка – началом координат.
x
y
z
O
Ось ординат
Ось абсцисс
Ось аппликат
j
i
k
Слайд 8Координаты вектора. Связь между координатами векторов и координатами точек.
Векторы i, j,
k – координатные вектора; единичный вектор.
Любой вектор а можно разложить можно представить в виде: a=xi+yj+zk
Координаты равных векторов соответственно равны.
Свойства :
a+b {x1+x2; y1+y2; z1+z2}
a-b {x1-x2; y1-y2; z1–z2}
ta {tx; ty; tz}
ОВ – ОА = АВ {x2-x1; y2-y1; z2–z1}
Любой вектор а можно разложить можно представить в виде: a=xi+yj+zk
Координаты равных векторов соответственно равны.
Свойства :
a+b {x1+x2; y1+y2; z1+z2}
a-b {x1-x2; y1-y2; z1–z2}
ta {tx; ty; tz}
ОВ – ОА = АВ {x2-x1; y2-y1; z2–z1}
Простейшие задачи в векторах.
А) координаты середины отрезка:
Б) длина вектора:
В) расстояние между двумя точками:
