С. Маршак
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике по теме Построение сечений многогранников
Содержание
- 1. Презентация по математике по теме Построение сечений многогранников
- 2. Слайд 2
- 3. Урок – проект
- 4. «Скажи мне – и я забуду.Покажи
- 5. Цель урока-проекта: Формирование
- 6. Задачи: 1. Изучить и проанализировать
- 7. «В геометрии нет царских дорог»
- 8. …Геометрия нужна,
- 9. 1 группа «Аналитики»
- 10. "Те, кто влюбляется в практику без теории,
- 11. Цель: Обобщение и систематизация изученного теоретического материала
- 12. Задачи:1. Повторить: а)Аксиомы стереометрии и следствия из
- 13. Аксиомы стереометрии Аксиома 1Через любые три точки,
- 14. Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскостиАксиома 2
- 15. Если две плоскости имеют общую точку, то
- 16. Следствия из аксиом стереометрии1. Через прямую и
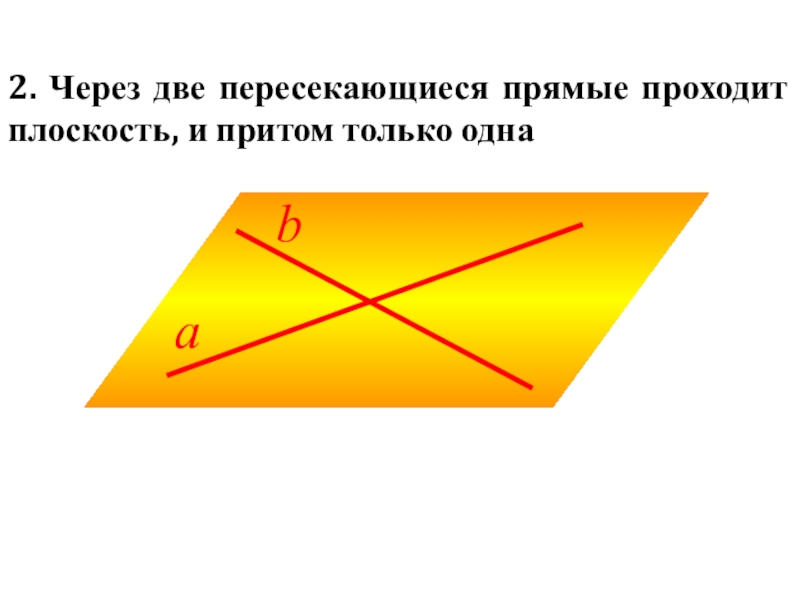
- 17. 2. Через две пересекающиеся прямые проходит плоскость, и притом только одна
- 18. Взаимное расположение в пространстве двух прямыхДве прямые
- 19. Взаимное расположение в пространстве двух прямыхНе лежат в одной плоскости: прямые скрещивающиесяm
- 20. Взаимное расположение в пространстве прямой и плоскости1. Прямая лежит в плоскости2. Прямая пересекает плоскость
- 21. 3. Прямая параллельна плоскости
- 22. Способы задания плоскостейПо трем точкам (аксиома 1)По
- 23. Вывод: Проанализировав
- 24. 2 группа «Теоретики» - 1
- 25. Цель:
- 26. Задачи: 1)Изучить литературу по теме, обобщить и
- 27. сечениеТолковый словарь: «сечение- фигура, образующаяся в месте пересечения какого-либо тела плоскостью»
- 28. Многоугольник, полученный при
- 29. Секущей плоскостью многогранника называется такая плоскость, по обе
- 30. Слайд 30
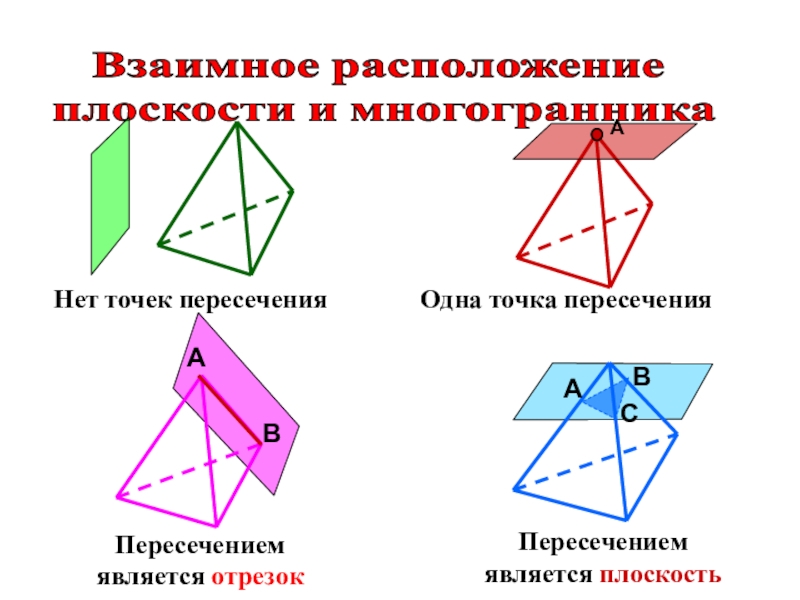
- 31. Взаимное расположение плоскости и многогранникаВАНет точек пересеченияОдна точка пересеченияПересечением является отрезокПересечением является плоскость
- 32. Виды сечений:Параллельное сечение-сечение, плоскость которого параллельна либо
- 33. Плоскость (в том числе и секущую)
- 34. Слайд 34
- 35. Слайд 35
- 36. Слайд 36
- 37. Слайд 37
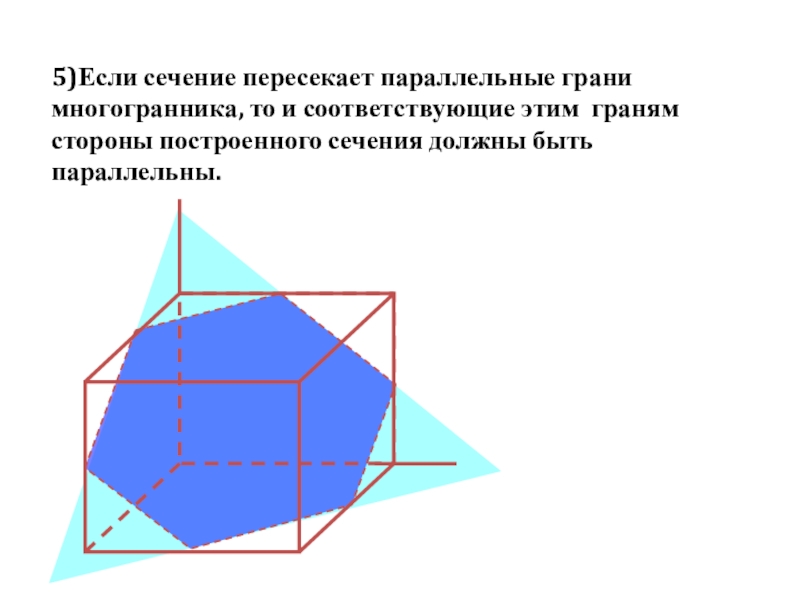
- 38. 5)Если сечение пересекает параллельные грани многогранника, то
- 39. 3 группа «Теоретики» - 2
- 40. Цель: Рассмотрение методов построения сечений многогранников
- 41. Задачи:1. Изучить литературу по теме, обобщить и
- 42. Поскольку
- 43. Слайд 43
- 44. Методы построения сеченийСуществует три основных метода построения сечений многогранников:Метод следов.Метод вспомогательных сечений.Комбинированный метод.
- 45. Метод следов и метод
- 46. Аксиоматический метод появился в Древней Греции, а
- 47. Слайд 47
- 48. Правила построения сечений методом следов
- 49. Правила построения сечений методом следов
- 50. Метод вспомогательных сечений
- 51. Комбинированный методКомбинированный метод построения сечений многогранников заключается
- 52. Задача на построение сечения многогранника плоскостью считается
- 53. Практическое применение Многогранники и многогранные поверхности широко
- 54. Выводы:
- 55. Выводы:
- 56. Гимнастика для глаз
- 57. Слайд 57
- 58. 4 группа «Практики» - 1
- 59. Цель: Исследование построения сечений тетраэдра аксиоматическим методом
- 60. Задачи:1. Изучить литературу по теме, обобщить и
- 61. Секущая плоскость тетраэдра - это
- 62. Сечения тетраэдраТетраэдр имеет 4 граниВ сечении может получиться:ТреугольникЧетырехугольник
- 63. Построение сечений тетраэдра
- 64. Если вы хотите научиться плавать, то смело
- 65. 1. Построить сечение тетраэдра АВМР плоскостью, проходящей
- 66. Задача для класса. Постройте сечение тетраэдра АВСS плоскостью, проходящей через заданные точкиМВАСNKS
- 67. D2. Постройте сечение тетраэдра , плоскостью, проходящей через заданные точки М, N и PBACMNPQX
- 68. АВСSЗадача для класса. Постройте сечение тетраэдра плоскостью,
- 69. 3. Построить сечение тетраэдра АВСР, проходящее
- 70. Выводы: Изучив и проанализировав
- 71. Гимнастика для глаз
- 72. Слайд 72
- 73. 5 группа «Практики» - 2
- 74. Цель: Исследование построения сечений параллелепипеда аксиоматическим методом
- 75. Задачи:1. Изучить литературу по теме, обобщить и
- 76. Секущая плоскость параллелепипеда- это
- 77. Параллелепипед имеет 6 гранейВ его сечении может получиться:ТреугольникЧетырехугольникПятиугольникШестиугольник
- 78. Построение сечений параллелепипеда
- 79. NВ1. Постройте сечение параллелепипеда, плоскостью, проходящей через заданные точки M, N, PACC₁B₁A₁PМDD₁Q
- 80. 1. Соединяем точки K и F, принадлежащие
- 81. МР3. Постройте сечение куба, проходящее через точки
- 82. 4. Построить сечение, определяемое параллельными прямыми АА1 и CC1 АА1В1С1D1СВD1. Прямая А1С12. Прямая АСАА1С1С - сечение
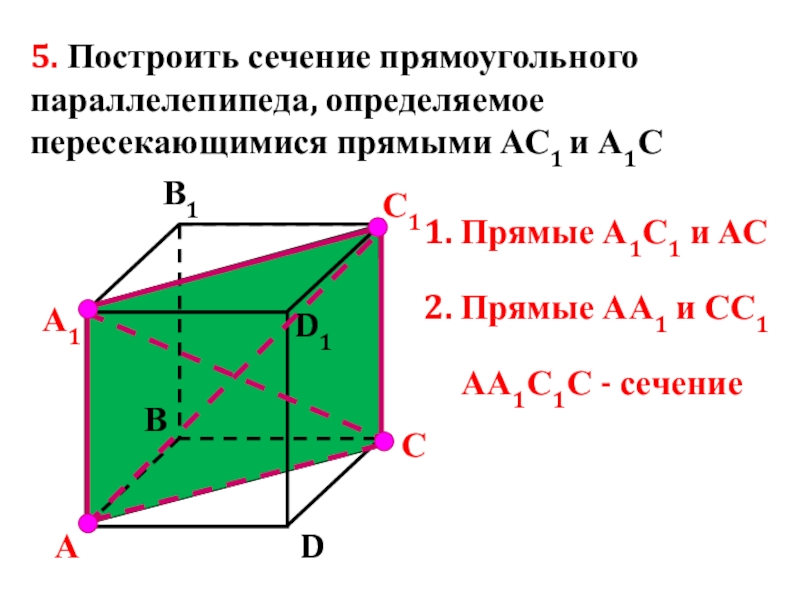
- 83. 5. Построить сечение прямоугольного параллелепипеда, определяемое пересекающимися
- 84. АА1В1С1D1DВС6. Постройте сечение куба плоскостью, проходящей через
- 85. АА1В1С1D1DС7. Построить сечения куба АВСДА1В1С1Д1 плоскостью, проходящей
- 86. Выводы: Изучив и проанализировав литературу
- 87. Гимнастика для глаз
- 88. Слайд 88
- 89. Самостоятельная работа
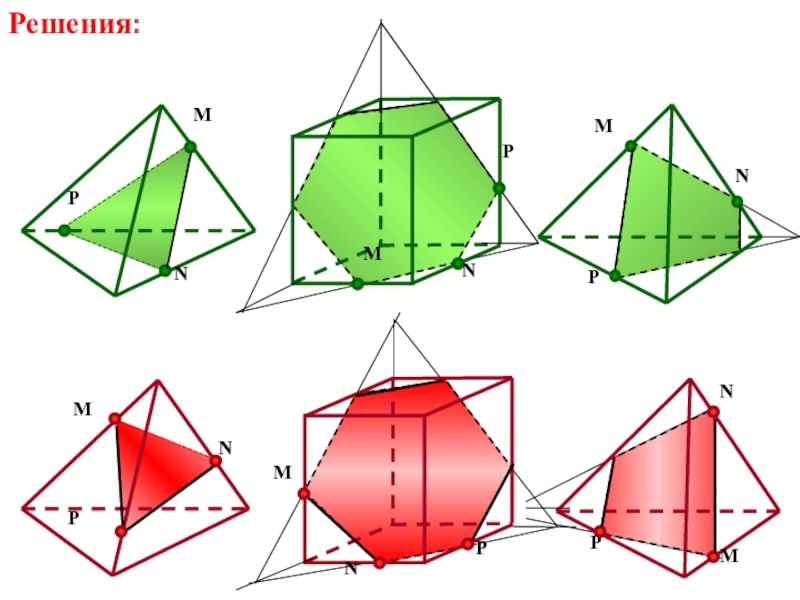
- 90. PNMNPMNPMРешения:MNPMNPMNP
- 91. повторил(а)…узнал(а)…- научился(лась)…- смог(ла), потому что …у меня
- 92. Домашнее задание: Составить две задачи на построение сечений многогранников (тетраэдр, параллелепипед)
- 93. Ресурсы:1. Атанасян Л.С. и др. Геометрия. Учебник для
Урок – проект по теме «Построение сечений многогранников»
Слайд 1Пусть каждый день и каждый час Вам новое добудет. Пусть добрым будет ум
у вас,
А сердце умным будет.
Слайд 4 «Скажи мне – и я забуду.
Покажи мне – и я
запомню.
Вовлеки меня – и я научусь»
Древняя китайская пословица
Вовлеки меня – и я научусь»
Древняя китайская пословица
Слайд 5Цель урока-проекта:
Формирование универсальных учебных
действий и умений обучающихся, необходимых для самостоятельного приобретения знаний в процессе изучения темы
«Построение сечений многогранников»
«Построение сечений многогранников»
Слайд 6Задачи:
1. Изучить и проанализировать необходимую учебно-методическую литературу по
теме;
2. Продолжить формирование информационной компетентности обучающихся;
3. Организовать процесс изучения темы с использованием дидактических средств и технологий , направленный на формирование универсальных учебных действий, обеспечивающих умение навыков самостоятельности и саморазвития; 4. Создать условия, способствующие повышению уровня мотивации к изучению предмета, повышению качественной успеваемости по математике; 5. Провести анализ, систематизацию и обобщение результатов, полученных в ходе урока – проекта по данной теме.
2. Продолжить формирование информационной компетентности обучающихся;
3. Организовать процесс изучения темы с использованием дидактических средств и технологий , направленный на формирование универсальных учебных действий, обеспечивающих умение навыков самостоятельности и саморазвития; 4. Создать условия, способствующие повышению уровня мотивации к изучению предмета, повышению качественной успеваемости по математике; 5. Провести анализ, систематизацию и обобщение результатов, полученных в ходе урока – проекта по данной теме.
Слайд 8 …Геометрия нужна, но она ведь так сложна! То фигуры, то тела,
не разберёшься.
Аксиомы там нужны,
Теоремы так важны,
Их учи - и результата ты добьёшься!
Слайд 10"Те, кто влюбляется в практику без теории, уподобляются мореплавателю, садящемуся на
корабль без руля и компаса и потому никогда не знающему, куда он плывет"
Леонардо да Винчи
http://blogs.nnm.ru/page6/
Слайд 12Задачи:
1. Повторить:
а)Аксиомы стереометрии и следствия из них;
б)Взаимное расположение двух прямых,
прямой и плоскости в пространстве;
в)Способы задания плоскостей;
2. Выяснить значимость данной темы.
в)Способы задания плоскостей;
2. Выяснить значимость данной темы.
Слайд 13Аксиомы стереометрии
Аксиома 1
Через любые три точки, не лежащие на одной
прямой, проходит плоскость, и притом только одна
Слайд 14Если две точки прямой лежат в плоскости, то все точки прямой
лежат в этой плоскости
Аксиома 2
Слайд 15Если две плоскости имеют общую точку, то они имеют общую прямую,
на которой лежат все общие точки этих плоскостей
Аксиома 3
В таком случае говорят, что плоскости пересекаются по прямой
Слайд 16Следствия
из аксиом стереометрии
1. Через прямую и не лежащую на ней
точку проходит плоскость, и притом только одна
Слайд 18Взаимное расположение
в пространстве двух прямых
Две прямые лежат в одной плоскости:
2.
Прямые
пересекаются
пересекаются
1. Прямые
параллельны
Одна общая точка
Нет общих точек
Слайд 19Взаимное расположение
в пространстве двух прямых
Не лежат в одной плоскости:
прямые
скрещивающиеся
m
Слайд 20Взаимное расположение
в пространстве прямой и плоскости
1. Прямая лежит в плоскости
2.
Прямая пересекает плоскость
Слайд 22Способы задания плоскостей
По трем точкам
(аксиома 1)
По прямой и не лежащей
на ней точке (следствие 1)
По двум пересекающимся
прямым (следствие 2)
По двум параллельным прямым ( определение параллельных прямых)
Слайд 23 Вывод: Проанализировав изученную теорию мы пришли к выводу, что полученные знания
необходимы для построения сечений многогранников на основе аксиоматики
Слайд 26Задачи:
1)Изучить литературу по теме, обобщить и систематизировать данный материал;
2) Проанализировать взаимное расположение плоскости и многогранника;
3) Рассмотреть понятие сечения многогранника и его виды;
4) Выяснить, что является сечением многогранника и что значит построить сечение многогранника плоскостью;
5) Рассмотреть способы задания плоскостей;
6) Выяснить, когда задача на построение сечения многогранника плоскостью считается решенной.
3) Рассмотреть понятие сечения многогранника и его виды;
4) Выяснить, что является сечением многогранника и что значит построить сечение многогранника плоскостью;
5) Рассмотреть способы задания плоскостей;
6) Выяснить, когда задача на построение сечения многогранника плоскостью считается решенной.
Слайд 27сечение
Толковый словарь: «сечение- фигура, образующаяся в месте пересечения какого-либо тела плоскостью»
Слайд 28 Многоугольник, полученный при пересечении многогранника и плоскости,
называется сечением многогранника указанной плоскостью
Многоугольник состоит из всех точек, которые являются общими для многогранника и секущей плоскости
Многоугольник состоит из всех точек, которые являются общими для многогранника и секущей плоскости
Слайд 29
Секущей плоскостью многогранника называется такая плоскость, по обе стороны от которой есть
точки данного многогранника
Секущая плоскость пересекает грани многогранника по отрезкам, поэтому сечение многогранника есть многоугольник, лежащий в секущей плоскости. Очевидно, что количество сторон этого многоугольника не может превышать количества граней данного многогранника.
Секущая плоскость пересекает грани многогранника по отрезкам, поэтому сечение многогранника есть многоугольник, лежащий в секущей плоскости. Очевидно, что количество сторон этого многоугольника не может превышать количества граней данного многогранника.
Слайд 30 Построить сечение многогранника плоскостью- это значит указать точки пересечения секущей плоскости с
ребрами многогранника и соединить их отрезками, принадлежащими граням многогранника
Слайд 31Взаимное расположение
плоскости и многогранника
В
А
Нет точек пересечения
Одна точка пересечения
Пересечением
является отрезок
Пересечением
является плоскость
Слайд 32Виды сечений:
Параллельное сечение-
сечение, плоскость которого параллельна
либо основанию,
либо одной из
грани многогранника
Диагональное сечение-
сечение, плоскость которого
проходит через диагонали
многогранника
и диагонали оснований многогранника.
Слайд 33Плоскость (в том числе и секущую) можно задать
следующим
образом
Тремя точками, не лежащими на одной прямой
Прямой и точкой, не
лежащей на ней
Двумя
пересекающимися
прямыми
Двумя
параллельными
прямыми
Слайд 34
Выводы:
Изучив и проанализировав литературу по теме: «Сечения многогранника, мы выяснили, что:
1) Построенное сечение выпуклого многогранника всегда выпуклый многоугольник;
Слайд 36
Выводы:
3)Точки, лежащие на гранях многогранника, обязательно должны лежать на сторонах многоугольника, полученного в сечении;
3)Точки, лежащие на гранях многогранника, обязательно должны лежать на сторонах многоугольника, полученного в сечении;
Слайд 37
Выводы:
4)Две стороны многоугольника, получившегося в сечении, не могут принадлежать одной грани данного многогранника;
4)Две стороны многоугольника, получившегося в сечении, не могут принадлежать одной грани данного многогранника;
Слайд 38
5)Если сечение пересекает параллельные грани многогранника, то и соответствующие этим граням
стороны построенного сечения должны быть параллельны.
Слайд 41Задачи:
1. Изучить литературу по теме, обобщить и систематизировать данный материал;
2. Рассмотреть
различные методы построения сечений многогранников;
3. Показать значимость данной темы и применение ее в реальной жизни.
3. Показать значимость данной темы и применение ее в реальной жизни.
Слайд 42
Поскольку плоскость определяется:
тремя точками;
прямой и
точкой;
двумя параллельными прямыми;
двумя пересекающимися прямыми,
построение плоскости сечения проходит в зависимости от задания этой плоскости. Поэтому все способы построения сечений многогранников можно разделить на методы.
двумя параллельными прямыми;
двумя пересекающимися прямыми,
построение плоскости сечения проходит в зависимости от задания этой плоскости. Поэтому все способы построения сечений многогранников можно разделить на методы.
Слайд 44Методы построения сечений
Существует три основных метода построения сечений многогранников:
Метод следов.
Метод вспомогательных сечений.
Комбинированный метод.
Слайд 45 Метод следов и метод вспомогательных сечений являются разновидностями аксиоматического
метода построения сечений
Методы построения сечений
1.Аксиоматический метод ( метод следов, метод вспомогательных сечений ) 2. Комбинированный метод
Методы построения сечений
1.Аксиоматический метод ( метод следов, метод вспомогательных сечений ) 2. Комбинированный метод
Слайд 46Аксиоматический метод появился в Древней Греции, а сейчас применяется во всех
теоретических науках, прежде всего в математике
Слайд 47
Метод следов
Суть метода заключается в построении вспомогательной прямой, являющейся изображением линии пересечения секущей плоскости с плоскостью какой-либо грани фигуры. Удобнее всего строить изображение линии пересечения секущей плоскости с плоскостью нижнего основания. Эту линию называют следом секущей плоскости. Используя след, легко построить изображения точек секущей плоскости, находящихся на боковых ребрах или гранях фигуры
Суть метода заключается в построении вспомогательной прямой, являющейся изображением линии пересечения секущей плоскости с плоскостью какой-либо грани фигуры. Удобнее всего строить изображение линии пересечения секущей плоскости с плоскостью нижнего основания. Эту линию называют следом секущей плоскости. Используя след, легко построить изображения точек секущей плоскости, находящихся на боковых ребрах или гранях фигуры
Слайд 48Правила построения сечений методом следов
Если даны (или
уже построены) две точки плоскости сечения на одной грани многогранника, то след сечения этой плоскости – прямая, проходящая через эти точки
Слайд 49Правила построения сечений методом следов
Если
дана (или уже построена) прямая пересечения плоскости сечения с основанием многогранника (след на основании) и есть точка, принадлежащая определённой боковой грани, то нужно определить точку пересечения данного следа с этой боковой гранью (точка пересечения данного следа с общей прямой основания и данной боковой грани)
Точку пересечения плоскости сечения с основанием можно определить, как точку пересечения какой-либо прямой в плоскости сечения с её проекцией на плоскость основания.
Точку пересечения плоскости сечения с основанием можно определить, как точку пересечения какой-либо прямой в плоскости сечения с её проекцией на плоскость основания.
Слайд 50
Метод вспомогательных сечений
Этот метод построения сечений
многогранников является в достаточной мере универсальным. В тех случаях, когда нужный след (или следы секущей плоскости) оказывается за пределами чертежа, этот метод имеет даже определенные преимущества. Вместе с тем следует иметь в виду, что построения, выполняемые при использовании этого метода, зачастую получаются «искусственные». Тем не менее в некоторых случаях метод вспомогательных сечений оказывается наиболее рациональным.
Слайд 51Комбинированный метод
Комбинированный метод построения сечений многогранников заключается в том, что при
построении этим методом на каких-то этапах построения сечения применяются приёмы метода следа, а на каких-то применяются теоремы о параллельности прямых и плоскостей в пространстве.
Суть комбинированного метода построения сечений многогранников состоит в применении теорем о параллельности прямых и плоскостей в пространстве в сочетании с аксиоматическим методом
Суть комбинированного метода построения сечений многогранников состоит в применении теорем о параллельности прямых и плоскостей в пространстве в сочетании с аксиоматическим методом
Слайд 52Задача на построение сечения многогранника плоскостью считается решенной,
когда плоскость пересекает многогранник
по его внутренности, то пересечением данной плоскости с каждой гранью этого многогранника будет некоторый отрезок. Таким образом, задача считается решенной, если найдены все отрезки, по которым плоскость пересекает грани многогранника
Слайд 53Практическое применение
Многогранники и многогранные поверхности широко применяются в архитектуре и
строительстве.
Любое строительство начинается с чертежа того объекта, который предстоит создать. Его нужно рассматривать в разных проекциях и в разных сечениях.
Один из примеров Исаакиевский собор в Санкт-Петербурге.
Любое строительство начинается с чертежа того объекта, который предстоит создать. Его нужно рассматривать в разных проекциях и в разных сечениях.
Один из примеров Исаакиевский собор в Санкт-Петербурге.
Слайд 54Выводы:
Изучив литературу по
теме, мы выяснили, что существует 3 основных метода построения сечений многогранников;
В тех случаях, когда применение метода следа затруднено, применяют метод вспомогательных сечений или комбинированный метод;
Мы узнали, что задача на построение сечения многогранника считается полностью решенной, если найдены все отрезки, по которым плоскость пересекает грани многогранника;
Знание методов построения сечений, способов нахождения точек и линий пересечения секущих плоскостей нам поможет решать задачи на построение сечений на различных геометрических телах.
В тех случаях, когда применение метода следа затруднено, применяют метод вспомогательных сечений или комбинированный метод;
Мы узнали, что задача на построение сечения многогранника считается полностью решенной, если найдены все отрезки, по которым плоскость пересекает грани многогранника;
Знание методов построения сечений, способов нахождения точек и линий пересечения секущих плоскостей нам поможет решать задачи на построение сечений на различных геометрических телах.
Слайд 55Выводы:
Мы выяснили, что тема
« Построение сечений многогранников» занимает важное место в курсе геометрии. Применяется в некоторых разделах физики, в теоретической механике, гидравлике.
Методы построения сечений многогранников находят широкое применение в реальной жизни. Их знание необходимы ювелирам, дизайнерам, инженерам, токарям.
В процессе работы мы систематизировали материал по теме «Построение сечений многогранников» и поняли, что построения сечений многогранников являются важной составляющей проектирования какого-либо сооружения, то есть повсеместно применяются в архитектуре.
Методы построения сечений многогранников находят широкое применение в реальной жизни. Их знание необходимы ювелирам, дизайнерам, инженерам, токарям.
В процессе работы мы систематизировали материал по теме «Построение сечений многогранников» и поняли, что построения сечений многогранников являются важной составляющей проектирования какого-либо сооружения, то есть повсеместно применяются в архитектуре.
Слайд 60Задачи:
1. Изучить литературу по теме, обобщить и систематизировать данный материал;
2. Исследовать,
какие фигуры возможны при построении сечений тетраэдра;
3. Классифицировать задачи с учетом задания точек сечения;
4. Рассмотреть построение сечений тетраэдра аксиоматическим методом;
5. Составить алгоритм построения сечения.
3. Классифицировать задачи с учетом задания точек сечения;
4. Рассмотреть построение сечений тетраэдра аксиоматическим методом;
5. Составить алгоритм построения сечения.
Слайд 61 Секущая плоскость тетраэдра - это любая плоскость, по обе
стороны от которой имеются точки данного тетраэдра
Многоугольник, сторонами которого являются отрезки, пересекающие грани тетраэдра называется сечением тетраэдра
Так как количество сторон многоугольника, полученного при построении сечения тетраэдра не может превышать количества граней данного тетраэдра, а он имеет 4 грани, то в сечении могут получаться треугольник или 4-угольник
Слайд 62Сечения тетраэдра
Тетраэдр имеет 4 грани
В сечении может получиться:
Треугольник
Четырехугольник
Слайд 64Если вы хотите научиться плавать, то смело входите в воду, а
если хотите научиться решать задачи, то решайте их.
(Д. Пойа)
(Д. Пойа)
Слайд 651. Построить сечение тетраэдра АВМР плоскостью, проходящей через три заданные точки
K, L, M
K
M
L
Прямая КМ
2. Прямая МL
3. Прямая КL
КМL –сечение
А
В
Р
Слайд 66Задача для класса. Постройте сечение тетраэдра АВСS плоскостью, проходящей через заданные
точки
М
В
А
С
N
K
S
Слайд 67D
2. Постройте сечение тетраэдра , плоскостью, проходящей через заданные точки М,
N и P
B
A
C
M
N
P
Q
X
Слайд 68А
В
С
S
Задача для класса. Постройте сечение тетраэдра плоскостью, проходящей через данные точки
D, Е, K.
D
E
K
M
F
Построение:
2. ЕК
3. ЕК ∩ АС = F
4. FD
5. FD ∩ BС = M
6. KM
1. DE
DЕKМ – искомое сечение
Слайд 693. Построить сечение тетраэдра АВСР, проходящее через прямую BC и
точку М
А
В
С
Р
М
1. Прямая ВС
2. Прямая СМ
ВСМ - сечение
3. Прямая ВМ
Слайд 70 Выводы: Изучив и проанализировав литературу по теме: «Построение сечений многогранников» мы классифицировали
задачи с учетом задания точек сечения тетраэдра и выяснили алгоритм построения сечения:
1) Если даны 3 точки, то нужно выяснить где они находятся. Если пара точек, лежит в одной грани (в одной плоскости), проводим через них прямую.
2) Выясняем, лежит ли третья точка в плоскости какой-то грани или в её продолжении.
3) Если в плоскости грани отмечена только одна точка, принадлежащая плоскости сечения, то надо построить дополнительную точку.
Для этого необходимо найти точки пересечения уже построенных прямых с другими прямыми, лежащими в тех же гранях.
4) Если даны точка и прямая или две прямые, то выясняем, где они находятся, что мы знаем о них. Проводим через них плоскость.
Слайд 75Задачи:
1. Изучить литературу по теме, обобщить и систематизировать данный материал;
2. Исследовать,
какие фигуры могут получаться при построении сечений параллелепипеда;
3. Классифицировать задачи с учетом задания точек сечения;
4. Рассмотреть построение сечений параллелепипеда аксиоматическим методом;
5. Составить алгоритм построения сечений.
3. Классифицировать задачи с учетом задания точек сечения;
4. Рассмотреть построение сечений параллелепипеда аксиоматическим методом;
5. Составить алгоритм построения сечений.
Слайд 76 Секущая плоскость параллелепипеда- это любая плоскость, по обе
стороны от которой имеются точки данного параллелепипеда
Многоугольник, сторонами которого являются отрезки, пересекающие грани параллелепипеда называется сечением параллелепипеда
Количество сторон этого многоугольника, полученного в сечении параллелепипеда не может превышать количества его граней
Слайд 77Параллелепипед имеет 6 граней
В его сечении
может получиться:
Треугольник
Четырехугольник
Пятиугольник
Шестиугольник
Слайд 79N
В
1. Постройте сечение параллелепипеда, плоскостью, проходящей через заданные точки M, N,
P
A
C
C₁
B₁
A₁
P
М
D
D₁
Q
Слайд 801. Соединяем точки K и F, принадлежащие одной грани А1В1С1D1.
2. Построить
сечение плоскостью, проходящей через данные точки Е, F, K
К
L
М
Построение:
1. KF
2. FE
3. FE ∩ АB = L
EFKNM – искомое сечение
F
E
N
4. LN ║ FK
6. EM
5. LN ∩ AD = M
7. KN
2. Соединяем точки F и E, принадлежащие одной грани АА1В1В.
3. Прямые FE и АВ, лежащие в одной грани АА1В1В, пересекаются в точке L
4. Проводим прямую LN параллельно FK (если секущая плоскость пересекает противоположные грани, то она пересекает их по параллельным отрезкам)
5. Прямая LN пересекает ребро AD в точке M
6. Соединяем точки Е и М, принадлежащие одной грани АА1D1D.
7. Соединяем точки К и N, принадлежащие одной грани ВСС1В1.
Слайд 81М
Р
3. Постройте сечение куба, проходящее через точки P, М, К
К
А
1.
Прямая МК
В
2. Прямая КР
О
Т
3. Прямая ОТ
МАВРС –искомое сечение
С
Слайд 824. Построить сечение, определяемое параллельными прямыми АА1 и CC1
А
А1
В1
С1
D1
С
В
D
1. Прямая
А1С1
2. Прямая АС
АА1С1С - сечение
Слайд 835. Построить сечение прямоугольного параллелепипеда, определяемое пересекающимися прямыми АС1 и А1С
А
А1
В1
С1
D1
D
В
С
1. Прямые А1С1 и АС
2. Прямые АА1 и СС1
АА1С1С - сечение
Слайд 84А
А1
В1
С1
D1
D
В
С
6. Постройте сечение куба плоскостью, проходящей через точку М и прямую
АС
М
1. Прямая СМ
2. Прямая МК II AC
3. Прямая AK
AKМС - сечение
Слайд 85А
А1
В1
С1
D1
D
С
7. Построить сечения куба АВСДА1В1С1Д1 плоскостью, проходящей через ребро А1Д1 и
середину ребра ВВ1
В
1. Прямая А1М
3. Прямая D1K
A1D1KM - сечение
А1D1
Слайд 86 Выводы: Изучив и проанализировав литературу по теме: «Построение сечений многогранников»
мы классифицировали задачи с учетом задания точек сечения параллелепипеда и выяснили:
Соединять можно только две точки, лежащие в плоскости одной грани.
Если нет по условию двух точек, лежащих в плоскости (одной грани многогранника) или одна из трёх точек находится внутри фигуры или же снаружи, находясь в пространстве, то сначала надо построить вспомогательную плоскость, которая пересекала бы основание данной фигуры или его продолжение, которая в свою очередь будет пересекать какие-то стороны основания или их продолжение.
Секущая плоскость пересекает параллельные грани по параллельным отрезкам.
Слайд 91повторил(а)…
узнал(а)…
- научился(лась)…
- смог(ла), потому что …
у меня не получилось, потому что…
дома
надо потренироваться…
Интересно ли было тебе на уроке?
Узнал ли ты что-либо новое для себя?
Интересно ли было тебе на уроке?
Узнал ли ты что-либо новое для себя?
Рефлексия:
Сегодня на уроке я…
Слайд 92Домашнее задание:
Составить две задачи на
построение сечений многогранников (тетраэдр, параллелепипед)
Слайд 93Ресурсы:
1. Атанасян Л.С. и др. Геометрия. Учебник для 10-11 классов общеобразовательных учреждений
2. Изображение с сайта: http://www.cdvseti.ru/id3700.html 3. Портреты математиков взяты с диска "Математика 5-11". Изображение с сайта: http://www.thg.ru/education/20050714/images/arhimed_cut.jpg
4. Анимация с сайта: http://badbad-girl.narod.ru/zelenie.html
5. https://sites.google.com/site/polyhedrasection2014/po..
6.http://открытыйурок.рф/статьи/411264/
7. https://docplayer.ru/30923930-Uchebnoe-posobie-dlya-u..
8. https://studwood.ru/1697455/pedagogika/ispolzovanie_m..
9. studwood.ru
10. http://slidegur.com/doc/1106520/metod-vspomogatel._ny..
11. https://sites.google.com/site/obrazovatelnyjresursgeometry/ho
me/tema-4-metody-postroenia-secenij-kombinirovannyj-metod
12. http://открытыйурок.рф/статьи/212754/
13. Электронное издание «1С: Школа. Математика, 5-11 кл. Практикум»14. Электронное издание «Решебник по геометрии. Пособие для абитуриентов. Полный курс за 7-11 классы» 14. https://nsportal.ru/shkola/geometriya/library/2012/01/03/postroenie-secheniy-mnogogrannikov-urok-10-klass
4. Анимация с сайта: http://badbad-girl.narod.ru/zelenie.html
5. https://sites.google.com/site/polyhedrasection2014/po..
6.http://открытыйурок.рф/статьи/411264/
7. https://docplayer.ru/30923930-Uchebnoe-posobie-dlya-u..
8. https://studwood.ru/1697455/pedagogika/ispolzovanie_m..
9. studwood.ru
10. http://slidegur.com/doc/1106520/metod-vspomogatel._ny..
11. https://sites.google.com/site/obrazovatelnyjresursgeometry/ho
me/tema-4-metody-postroenia-secenij-kombinirovannyj-metod
12. http://открытыйурок.рф/статьи/212754/
13. Электронное издание «1С: Школа. Математика, 5-11 кл. Практикум»14. Электронное издание «Решебник по геометрии. Пособие для абитуриентов. Полный курс за 7-11 классы» 14. https://nsportal.ru/shkola/geometriya/library/2012/01/03/postroenie-secheniy-mnogogrannikov-urok-10-klass
