- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике по теме Координаты вектора
Содержание
- 1. Презентация по математике по теме Координаты вектора
- 2. Прямоугольная система координат в пространстве. Оси координатЕсли
- 3. Определение луча на координатной плоскости. НаправлениеТочка О
- 4. А(3; -1; 0)В(0; 0; 7)С(2; 0; 0)D(-4;
- 5. ТЕМА: Координаты вектораНа каждой из положительных полуосей
- 6. Разложение по координатным векторамЛюбой вектор a можно
- 7. Коэффициенты х, у и z в разложении
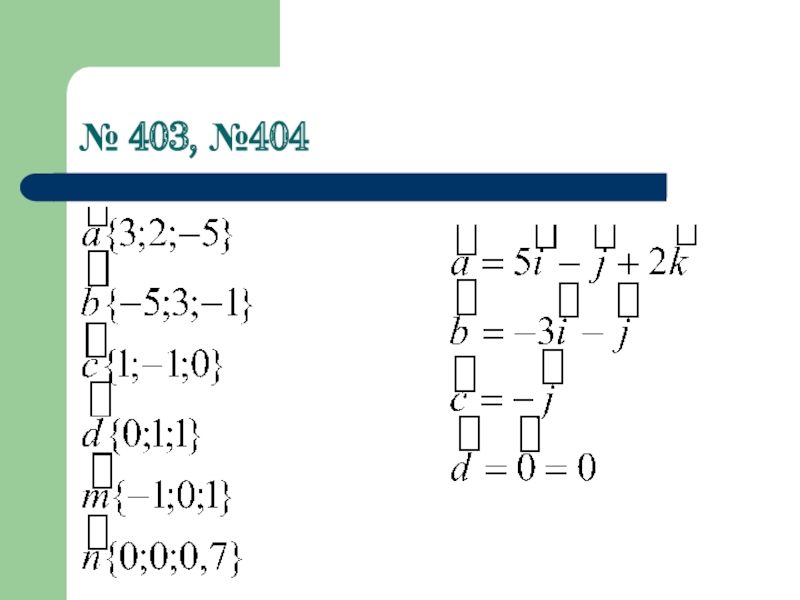
- 8. № 403, №404
- 9. Нулевой вектор и равные вектораТак как нулевой
- 10. Правила нахождения суммы, разности и произведения на
- 11. Правило №2Каждая координата разности двух векторов равна
- 12. Правило №3Каждая координата произведения вектора на число
- 13. № 407, №409
- 14. История возникновения понятия векторПонятие вектор возникло в
- 15. Вектор называется свободным, если его значение не
- 16. Примером скользящего вектора может служить сила, действующая
- 17. Например, сила, приложенная к некоторой точке упругого
- 18. Векторное исчисление- математическая дисциплина, в которой изучают
- 19. Возникновение и развитие векторного исчисления. Возникновение векторного
- 20. Основы векторного исчисления были заложены исследованиями английского
- 21. Современный вид векторному исчислению придал американский физик
- 22. Исследования казанского математика А. П. Котельникова по
- 23. Самостоятельно Даны векторы:1 вариант: Найти: 2 вариант:
- 24. Проверка в парах1 вариант: Найти: 2 вариант:
- 25. Домашнее задание№ 404, № 409, № 411
- 26. Спасибо за урок!
Прямоугольная система координат в пространстве. Оси координатЕсли через точку пространства проведены три попарно перпендикулярные прямые, на каждом из них выбрано направление(оно обозначается стрелкой) и выбрана единица измерения отрезков, то говорят, что задана прямоугольная система координат в
Слайд 2Прямоугольная система координат в пространстве. Оси координат
Если через точку пространства проведены
три попарно перпендикулярные прямые, на каждом из них выбрано направление(оно обозначается стрелкой) и выбрана единица измерения отрезков, то говорят, что задана прямоугольная система координат в пространстве.
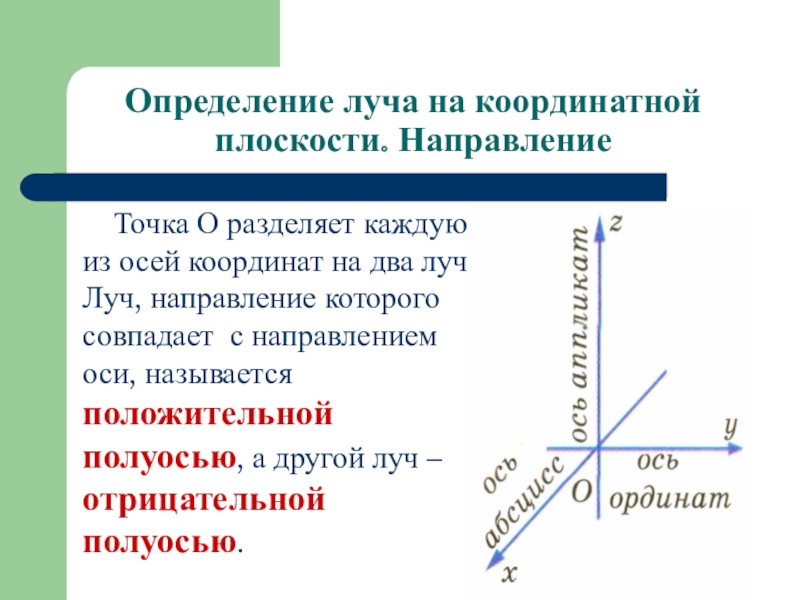
Слайд 3Определение луча на координатной плоскости. Направление
Точка О разделяет каждую из осей
координат на два луча. Луч, направление которого совпадает с направлением оси, называется положительной полуосью, а другой луч – отрицательной полуосью.
Слайд 4А(3; -1; 0)
В(0; 0; 7)
С(2; 0; 0)
D(-4; 0; 3)
E(0; -1; 0)
F(1;
2; 3)
G(0; 5; -7)
Ось абсцисс:
Ось ординат:
Ось аппликат:
Плоскость Оху:
Плоскость Охz:
Плоскость Оуz:
Какие из точек лежат:
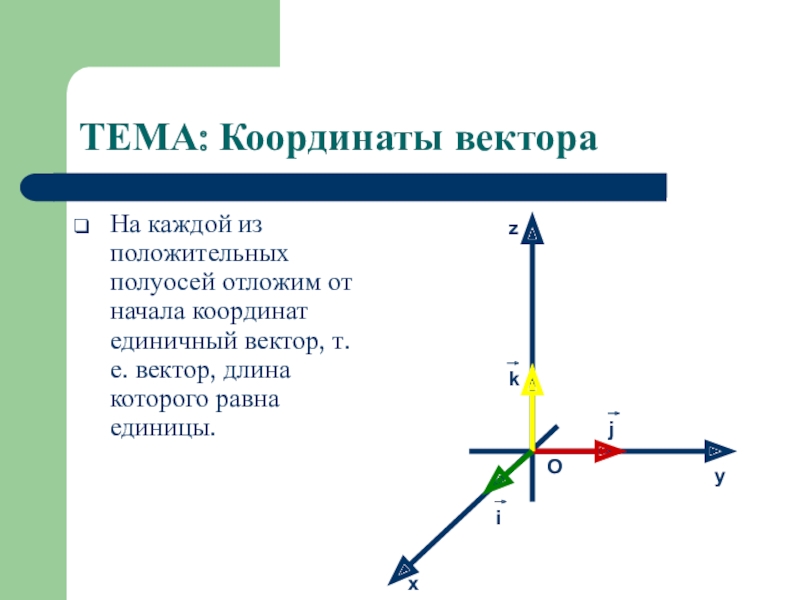
Слайд 5ТЕМА: Координаты вектора
На каждой из положительных полуосей отложим от начала координат
единичный вектор, т.е. вектор, длина которого равна единицы.
j
k
i
y
z
x
O
Слайд 6Разложение по координатным векторам
Любой вектор a можно разложить по координатным векторам,
т.е. представить в виде
а = xi + yj + zk
Причем коэффициенты разложения x, y, z определяются единственным образом.
а = xi + yj + zk
Причем коэффициенты разложения x, y, z определяются единственным образом.
Слайд 7Коэффициенты х, у и z в разложении вектора по координатным
векторам называются координатами вектора в данной системе координат.
Координаты вектора а будут записываться в фигурных скобках после обозначения вектора: а {x; y; z}.
а = xi + yj + zk
Слайд 9Нулевой вектор и равные вектора
Так как нулевой вектор можно представить в
виде 0 = 0i + 0j + 0k, то все координаты нулевого вектора равны нулю.
Координаты равных векторов соответственно равны, т.е. если векторы
a {x ; y ; z } и b {x ; y ; z } равны, то x =x , y =y и z =z .
Координаты равных векторов соответственно равны, т.е. если векторы
a {x ; y ; z } и b {x ; y ; z } равны, то x =x , y =y и z =z .
1
1
1
2
2
2
1
2
1
2
1
2
1
Слайд 10Правила нахождения суммы, разности и произведения на данное число
Каждая координата суммы
двух или более векторов равна сумме соответствующих координат этих векторов. Если a {x ; y ; z } и b {x ; y ; z } – данные векторы, то вектор a + b имеет координаты
{x +x ; y +y ; z +z }
{x +x ; y +y ; z +z }
1
2
1
2
1
2
2
2
2
1
1
1
Слайд 11Правило №2
Каждая координата разности двух векторов равна разности соответствующих координат этих
векторов. Если a {x ; y ; z } и b {x ; y ; z } – данные векторы, то вектор a – b имеет координаты
{x –x ; y –y ; z –z }
{x –x ; y –y ; z –z }
1
2
1
2
1
2
1
2
1
1
2
2
Слайд 12Правило №3
Каждая координата произведения вектора на число равна произведение соответствующей координаты
вектора на это число. Если a {x; y; z } – данный вектор, α - данное число, то вектор αa имеет координаты
{ x; y; z}
{ x; y; z}
α
α
α
Слайд 14История возникновения понятия вектор
Понятие вектор возникло в связи с изучением величин,
характеризуемых численным значением и направленностью (например, перемещение, скорость и ускорение движущейся материальной точки, действующая на неё сила и т.п.).
В механике и физике рассматривают свободные, скользящие и связанные вектора.
В механике и физике рассматривают свободные, скользящие и связанные вектора.
Слайд 15Вектор называется свободным, если его значение не меняется при произвольном параллельном
переносе.
Свободным вектором является, например, скорость движения материальной точки.
Вектор называется скользящим, если его значение не меняется при любом параллельном переносе вдоль линии его действия.
Свободным вектором является, например, скорость движения материальной точки.
Вектор называется скользящим, если его значение не меняется при любом параллельном переносе вдоль линии его действия.
Слайд 16Примером скользящего вектора может служить сила, действующая на
абсолютно твёрдое тело
(две равные и расположенные на одной прямой силы оказывают на абсолютно твёрдое тело одинаковое воздействие).
Вектор называется связанным, если фиксировано его начало.
Вектор называется связанным, если фиксировано его начало.
Слайд 17Например, сила, приложенная к некоторой точке упругого тела, представляет собой связанный
вектор.
Свойства свободных векторов изучаются средствами векторной алгебры (Векторное исчисление).
Общее понятие вектора, как элемента, так называемого, векторного пространства определяется аксиоматически.
Свойства свободных векторов изучаются средствами векторной алгебры (Векторное исчисление).
Общее понятие вектора, как элемента, так называемого, векторного пространства определяется аксиоматически.
Слайд 18Векторное исчисление- математическая дисциплина, в которой изучают свойства
операций над векторами
евклидова пространства.
При этом понятие вектора представляет собой математическую абстракцию величин, характеризующихся не только численным значением, но и направленностью (например, сила, ускорение, скорость).
При этом понятие вектора представляет собой математическую абстракцию величин, характеризующихся не только численным значением, но и направленностью (например, сила, ускорение, скорость).
Слайд 19Возникновение и развитие векторного исчисления.
Возникновение векторного исчисления тесно связано с
потребностями механики и физики.
До 19 в. для задания векторов использовался лишь координатный способ, и операции над векторами сводились к операциям над их координатами.
Лишь в середине 19 в. усилиями ряда учёных было создано векторное исчисление, в котором операции проводились непосредственно над векторами, без обращения к координатному способу задания.
До 19 в. для задания векторов использовался лишь координатный способ, и операции над векторами сводились к операциям над их координатами.
Лишь в середине 19 в. усилиями ряда учёных было создано векторное исчисление, в котором операции проводились непосредственно над векторами, без обращения к координатному способу задания.
Слайд 20Основы векторного исчисления были заложены исследованиями
английского математика
У. Гамильтона и
немецкого математика Г. Грассмана по гиперкомплексным числам (1844—50).
Их идеи были использованы английским физиком
Дж. К. Максвеллом в его работах
по электричеству и магнетизму.
Их идеи были использованы английским физиком
Дж. К. Максвеллом в его работах
по электричеству и магнетизму.
Слайд 21Современный вид векторному исчислению придал американский
физик Дж. Гиббс.
Значительный вклад
в развитие векторного исчисления внесли русские учёные. В первую очередь следует отметить работы М. В. Остроградского.
Им была доказана основная теорема векторного анализа (Остроградского формула).
Им была доказана основная теорема векторного анализа (Остроградского формула).
Слайд 22Исследования казанского математика А. П. Котельникова по развитию винтового исчисления
имели
важное значение для механики и геометрии.
Эти исследования были продолжены советскими математиками ПД. Н. Зейлигером и А. Широковым. Большое влияние на развитие В. и. имела книга «Векторный анализ», написанная в 1907 русским математиком П. О. Сомовым.
Эти исследования были продолжены советскими математиками ПД. Н. Зейлигером и А. Широковым. Большое влияние на развитие В. и. имела книга «Векторный анализ», написанная в 1907 русским математиком П. О. Сомовым.